Andrzej Wróbel

Fotogrametryczne opracowanie map

1. Autograf

1.1. Obserwacja stereoskopowa - przestrzenny znaczek pomiarowy

Sporządzenie mapy czy też pomiar pikiet wysokościowych na dwu niezależnych

zdjęciach sprawia wiele problemów z identyfikacją mierzonych punktów. Bardzo wyraźne
szczegóły jak np. narożniki budynków, ogrodzeń, załamania krawężników jezdni
i chodników, słupy można bez większego problemu pomierzyć niezależnie na dwóch
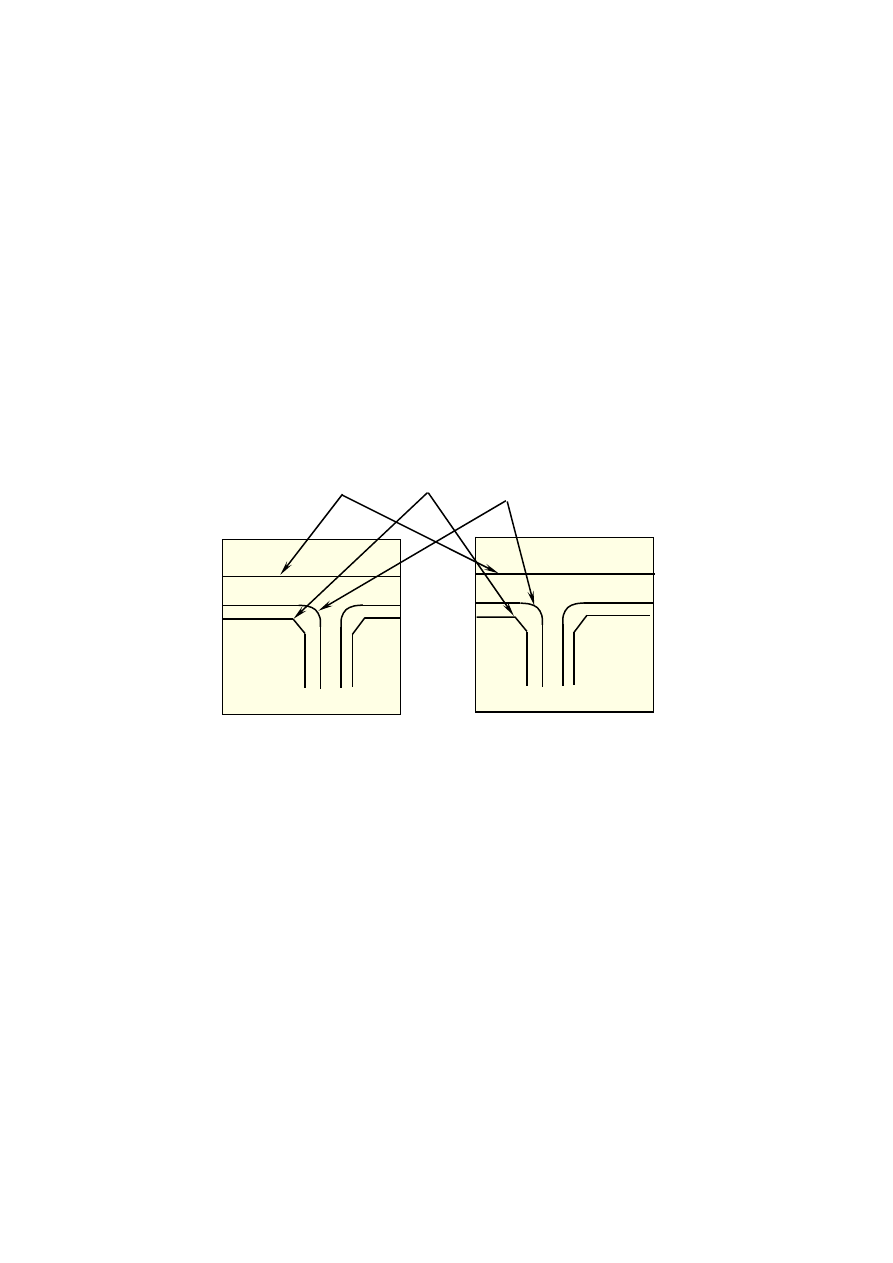
zdjęciach. Istnieje jednak duża grupa punktów, których dokładny pomiar w ten sposób nie jest
możliwy (rys.1.1). Są to wszelkiego rodzaju niewyraźne szczegóły (np. krawędzie skarp
ziemnych), punkty pośrednie na liniach prostych i łukach, pikiety wysokościowe osadzane
pośrodku pewnej powierzchni np. trawnika, użytku rolnego.

?

?

Rys. 1.1. Problem identyfikacji tych samych punktów na dwóch zdjęciach

Pomiar takich trudnych do niezależnej identyfikacji na dwóch zdjęciach punktów

umożliwia zastosowanie obserwacji stereoskopowej. Na tle obrazu każdego ze zdjęć
wprowadzany jest obraz znaczka pomiarowego. Umieszczenie obrazu znaczków obu zdjęć na
płaszczyźnie rdzennej powoduje, że obserwując te zdjęcia stereoskopowo widzimy
przestrzenny znaczek pomiarowy. Ponieważ widzimy go przestrzennie na tle przestrzennego
modelu możemy „dotykać” nim różnych miejsc modelu wykonując w ten sposób pomiar tych
miejsc.

1.2. Autograf – zasada budowy

Dwa sąsiednie pionowe zdjęcia lotnicze, wykonane z pokryciem podłużnym, umożliwiają

obserwację stereoskopową wspólnej ich części. Fakt ten wykorzystywany jest w przyrządzie
zwanym autografem. W autografie z dwóch zdjęć mających wspólne pokrycie (przeważnie
około 60%) tworzony jest model stereoskopowy a na tym modelu osadzając przestrzenny
znaczek pomiarowy rysuje się elementy sytuacji i mierzy wybrane punkty (np. pikiety).
W wyniku otrzymuje się w czasie rzeczywistym współrzędne mierzonych punktów
w przestrzennym, terenowym układzie współrzędnych. Aby było to możliwe musi być

wcześniej przeprowadzone tzw. orientacja modelu (zagadnienie to bardziej szczegółowo
zostanie omówione w dalszej części). W procesie orientacji zostaje utworzony metryczny
model przedstawiający sytuację z momentu wykonania zdjęć, czyli położenie zdjęć, przebieg
promieni tworzących obraz i odfotografowaną powierzchnię.

Autografy pod względem konstrukcji można podzielić na analogowe, analityczne

i cyfrowe.

lewe
zdjęcie

prawe
zdjęcie

baza zdjęć

w skali

zdjęcia mogą się obracać –
przyjmują orientację:

, , 

c

k

punkt

główny

punkt przecięcia

promieni – model

terenu w skali

takiej jak baza

dj ć

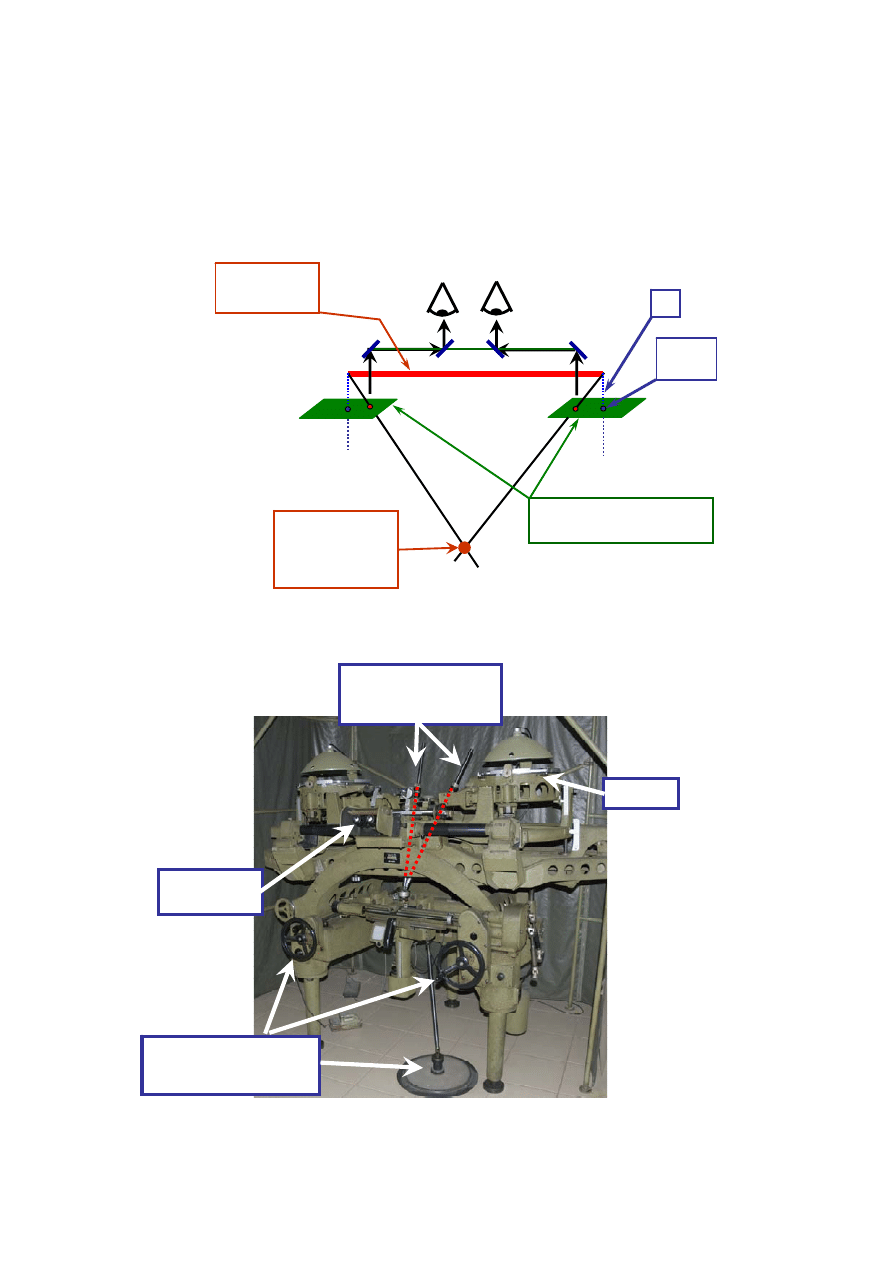
Rys. 1.2. Zasada budowy autografu analogowego

zdjęcie

układ

obserwacyjny

drążki metalowe

odtwarzające przebieg

promieni

urządzenia do sterowania
ruchem punktu przecięcia

drążków (promieni)

Rys. 1.3. Autograf mechaniczny A8 firmy Wild

W autografach analogowych, które przeszły już do historii, obserwowało się oryginały

zdjęć (lub ich fotograficzne pomniejszenia) a przebieg promieni odtwarzany był na drodze
optycznej lub mechanicznej (rys. 1.2). Przykładem autografu mechanicznego jest autograf A8
firmy Wild (rys. 1.3).

W autografach analitycznych zlikwidowano optyczną lub mechaniczną rekonstrukcję

promieni rzutujących i zastąpiono ją komputerem wykonującym tą rekonstrukcję na drodze
analitycznej. W dalszym ciągu obserwowało się jednak oryginalne zdjęcia.

W autografach cyfrowych oryginały zdjęć zastąpiono ich cyfrowymi kopiami

otrzymywanymi na drodze skanowania. W chwili obecnej w fotogrametrii, a zatem
i w autografach, coraz częściej, zamiast skanowanych zdjęć z kamer analogowych
wykorzystuje się zdjęcia cyfrowe z fotogrametrycznych kamer cyfrowych. Obrazy cyfrowe
wyświetlane są na ekranie komputera a do ich stereoskopowej obserwacji wykorzystuje się
różne metody np.:

 stereoskop (obrazy lewy i prawy wyświetlane są równocześnie na dwu połówkach

ekranu i obserwowane przez stereoskop lustrzany)

 anaglify (anaglif – nałożone na siebie obraz lewy i prawy w kolorach

dopełniających (czerwony i niebieskozielony (cyan) wyświetlane są na ekranie
a okulary w których lewe i prawe szkło są w odpowiadających kolorach
dopełniających umożliwiają lewym okiem obserwację tylko lewego obrazu
a prawym tylko prawego)

 pasywne i aktywne okulary (obraz lewy i prawy wyświetlane są naprzemiennie na

całym ekranie a okulary umożliwiają obserwację lewym okiem wtedy, gdy
wyświetlany jest lewy obraz a prawym, gdy wyświetlany jest prawy)

1.3. Autograf - zasada działania

Jak wspomniano wcześniej (rozdział 1.1) na lewe i prawe zdjęcie nakładane są

odpowiednio (w płaszczyźnie rdzennej) obrazy znaczka pomiarowego. Obserwacja
stereoskopowa tych obrazów znaczków powoduje, że widzimy znaczek pomiarowy
przestrzennie na tle przestrzennie obserwowanego modelu terenu. Ten przestrzenny znaczek
pomiarowy używamy jest do pomiaru i do rysowania w autografie. Przez operatora autografu
generowane są zmiany położenia znaczka w trójwymiarowej przestrzeni (X, Y, Z). Poprzez
odpowiednie urządzenie sterujące ( mysz + klawiatura, specjalne manipulatory) obserwator
podaje do komputera informacje o proponowanej zmianie położenia przestrzennego znaczka
pomiarowego. Ruch myszy lub manipulatora po stole podaje informację o wartościach

X,

Y, o które należy zmienić współrzędne X i Y. Użycie przycisków myszy, odpowiednich
klawiszy klawiatury, pokrętła lub przycisków manipulatora podaje informację o wartości

Z,

o którą należy zmienić współrzędną Z. Na podstawie informacji o proponowanej zmianie

X,

Y, Z komputer oblicza nowe przestrzenne współrzędne X, Y, Z znaczka pomiarowego,
następnie nowe położenie obrazów znaczka pomiarowego na lewym i prawym zdjęciu
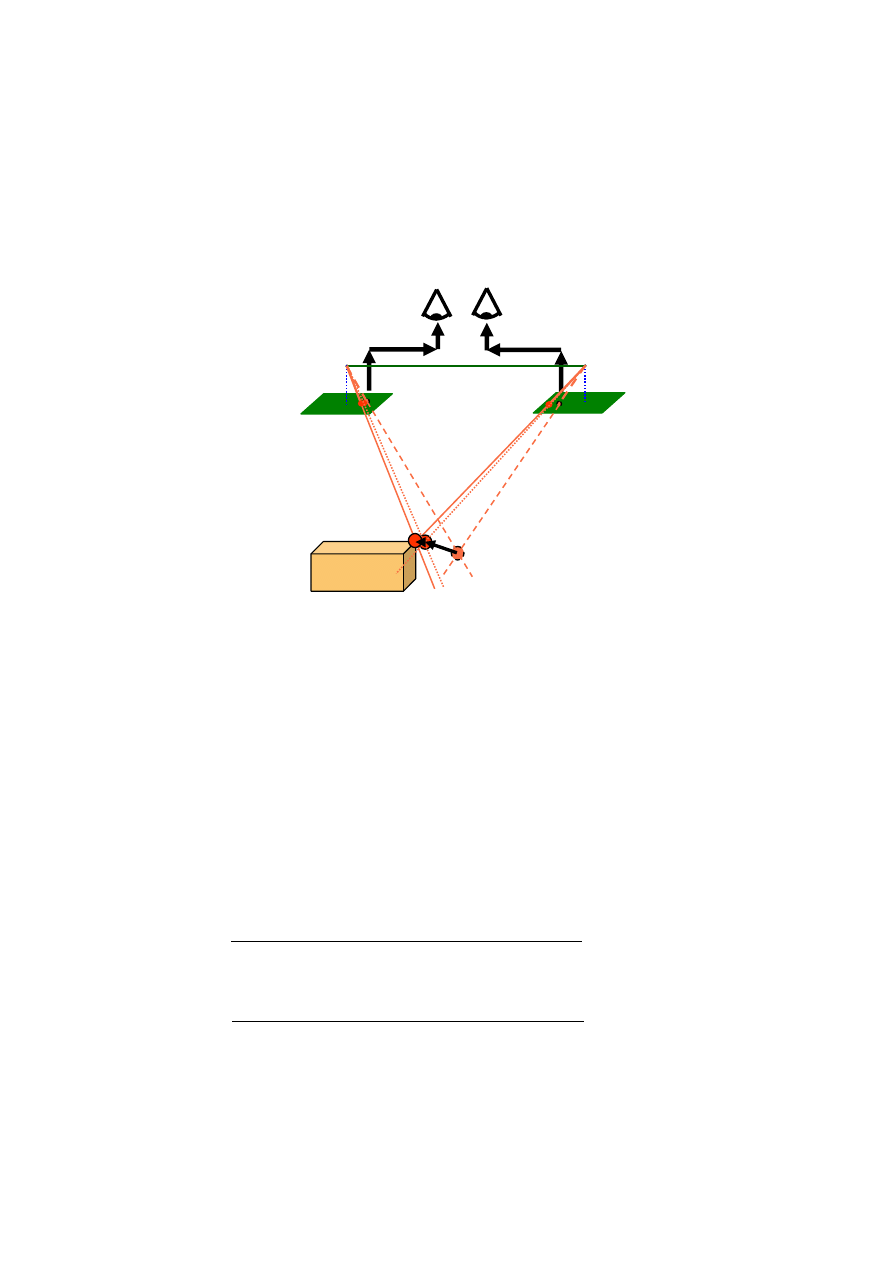
i umieszcza tam obrazy znaczka pomiarowego (rys. 1.4). Obserwator patrząc stereoskopowo
sprawdza czy znaczek dotknął wybranego punktu terenowego i jeżeli cel nie został jeszcze
osiągnięty ocenia jaka powinna być dalsza zmiana położenia przestrzennego znaczka
pomiarowego. Tak samo jak poprzednio wykorzystując odpowiednie urządzenie sterujące
podaje następną proponowaną zmianę współrzędny przestrzennych X, Y, Z. Komputer
ponownie wylicza nowe współrzędne X, Y, Z znaczka pomiarowego, odpowiadające im
punkty na lewym i prawym zdjęciu i umieszcza tam obrazy znaczka pomiarowego.
Obserwator patrząc stereoskopowo ponownie sprawdza czy znaczek już dotknął wybranego
punktu terenowego i jeżeli cel w dalszym ciągu nie został jeszcze osiągnięty ocenia jaka
powinna być dalsza zmiana położenia przestrzennego znaczka pomiarowego. Tak samo jak

poprzednio wykorzystując odpowiednie urządzenie sterujące ponownie podaje proponowaną
zmianę współrzędny przestrzennych X, Y, Z. I tak aż do skutku, czyli aż przestrzenny
znaczek pomiarowy dotknie przestrzennego modelu w wybranym punkcie. W tym momencie
obserwator rejestruje współrzędne X, Y, Z przestrzennego znaczka pomiarowego. Ponieważ
znaczek dotyka wybranego punktu współrzędne te są tożsame ze współrzędnymi tego
mierzonego punktu. Tak zarejestrowany punkt zapisywany jest w pamięci komputera, jako
pomierzona pikieta lub jako węzeł rysowanej linii łamanej.

Rys. 1.4. Wykorzystanie przestrzenne go znaczka pomiarowego do pomiaru w autografie

Sposób wyznaczenia położenia obrazów znaczków pomiarowych na zdjęciach można

wytłumaczyć wykorzystując równanie kolinearności (1.1).

(1.1)

R

A

r









T

1



gdzie

,





























O

P

O

P

O

P

Z

Z

Y

Y

X

X

R

























k

P

P

c

y

x

r

Równanie w postaci wektorowej (1.1) możemy rozpisać do postaci (patrz konspekt

„O równaniu kolinearności” - semestr letni):

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

33

23

13

32

22

12

33

23

13

31

21

11

O

P

O

P

O

P

O

P

O

P

O

P

k

P

O

P

O

P

O

P

O

P

O

P

O

P

k

P

Z

Z

a

Y

Y

a

X

X

a

Z

Z

a

Y

Y

a

X

X

a

c

y

Z

Z

a

Y

Y

a

X

X

a

Z

Z

a

Y

Y

a

X

X

a

c

x













































































(1.2)

W równaniu (1.1) i (1.2) w wektorze R występują współrzędne X

P

, Y

P

, Z

P

, które

w

naszym przypadku są współrzędnymi przestrzennego znaczka pomiarowego.

Wprowadzając urządzeniem sterującym zmiany położenia przestrzennego znaczka
pomiarowego wprowadzamy właśnie zmiany tych trzech współrzędnych. Komputer

z powyższego równania wylicza współrzędne x

P

, y

P

w wektorze r, czyli współrzędne obrazu

znaczka pomiarowego na zdjęciu. Obliczenia takie wykonuje się oczywiście dla obu zdjęć
uzyskując współrzędne x

P

’, y

P

’ na lewym zdjęciu i współrzędne x

P

”, y

P

” na prawym zdjęciu.

Aby możliwe było wykonanie powyższych obliczeń, w równaniu kolinearności, muszą

być znane stała kamery c

k

i elementy orientacji zewnętrznej zdjęć: współrzędne środka rzutów

X

O

’, Y

O

’, Z

O

’ i kąty obrotu



’,



’,



’ lewego zdjęcia a także współrzędne środka rzutów X

O

”,

Y

O

”, Z

O

” i kąty obrotu



”,



”,



” prawego zdjęcia. Należy również zwrócić uwagę, że

w wyniku obliczeń otrzymamy współrzędne na zdjęciach w układzie tłowym a bezpośrednio
z obrazu wyświetlanego na ekranie komputera możemy odczytać współrzędne w układzie
obrazowym (pikselowym). Wszystko to powoduje, iż nie możemy zaraz po wczytaniu zdjęć
do autografu przystąpić do pomiaru czy rysowania mapy. Musimy wpierw przygotować
odpowiednie dane dla programu. Etap ten nazywa się orientacją modelu.

1.4. Orientacja modelu (zdjęć) w autografie cyfrowym

Orientacja zdjęć w autografie cyfrowym składa się z dwóch etapów.

 Pierwszy z nich jest to znalezienie powiązania pomiędzy pikselowym układem

obrazowym a układem tłowym zdjęcia i nosi nazwę orientacja wewnętrzna
zdjęcia w autografie cyfrowym.

 Etap drugi to wprowadzenie stałej kamery c

k

znanej z raportu z kalibracji kamery

oraz wprowadzenie elementów orientacji zewnętrznej zdjęć. Elementy te mogą
być znane z wcześniejszych obliczeń np. z wykonanej wcześniej
aerotriangulacji. Jeżeli elementy te nie są znane to z reguły przeprowadza się
po orientacji wewnętrznej dwustopniową orientację składającą się z orientacji
wzajemnej i bezwzględnej.

1.4.1. Orientacja wewnętrzna zdjęcia w autografie cyfrowym

Zdjęcia fotogrametryczne opracowywane w autografie cyfrowym mogą pochodzić

z kamer analogowych lub cyfrowych. Zdjęcia z kamer analogowych przed wprowadzeniem
do komputera muszą być zeskanowane na skanerze fotogrametrycznym. Wszelkie pomiary na
zdjęciu cyfrowym wyświetlanym na ekranie komputera wykonuje się w obrazowym
(pikselowym) układzie obrazu. W zależności od tego czy zdjęcie pochodzi bezpośrednio
z kamery cyfrowej czy też było skanowane różna jest zależność pomiędzy układem
obrazowym a układem tłowym.

Zdjęcia analogowe a następnie skanowane

W skanerze układ pikselowy jest definiowany przez prowadnice skanera. Zdjęcie

skanowane jest układane na nośniku skanera w miarę dokładnie równolegle do tych
prowadnic. Nie jest to jednak idealna równoległość w związku, z czym układ tłowy (o osiach
równoległych do ramki tłowej) jest lekko skręcony w stosunku do układu obrazowego
(pikselowego).

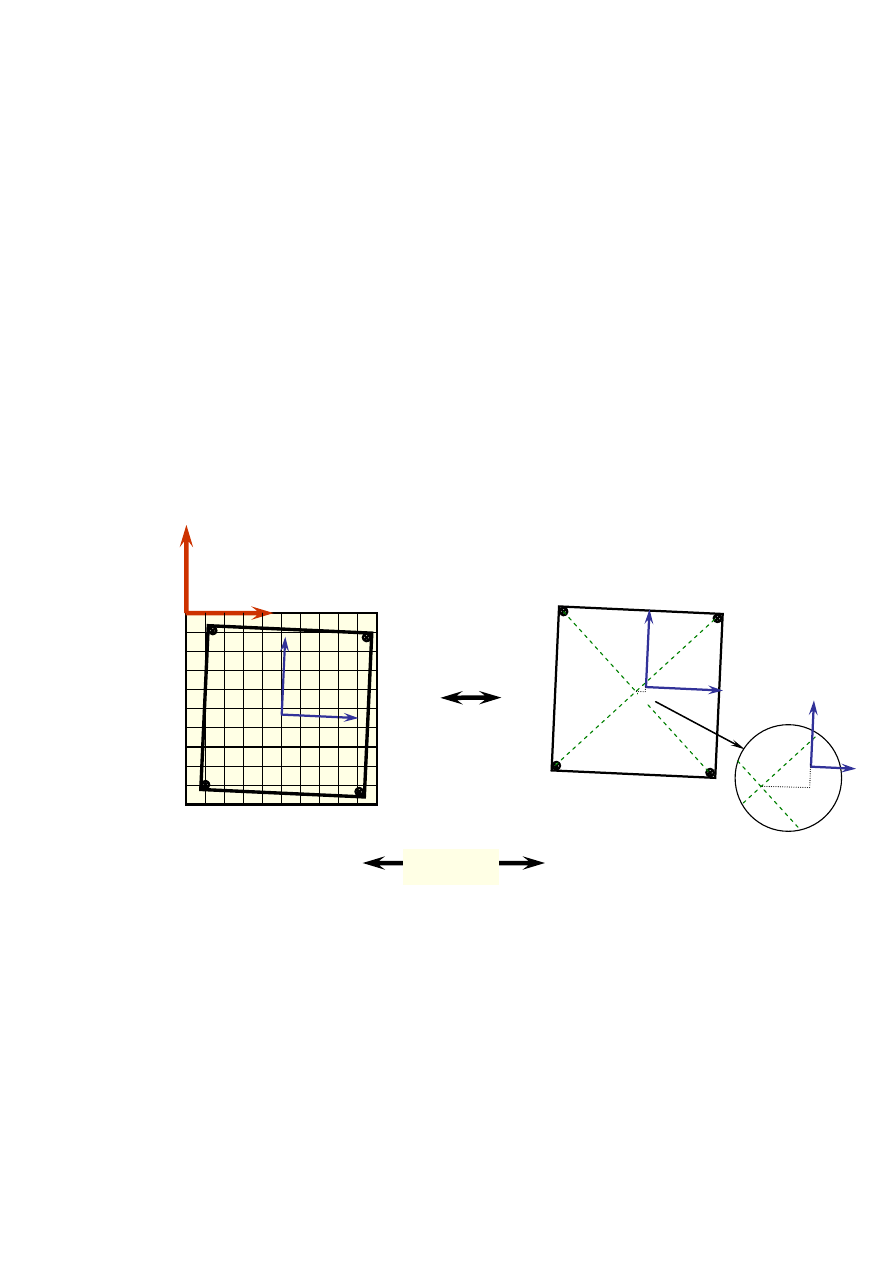
Orientacja wewnętrzna dla zdjęć analogowych a następnie skanowanych polega na

wyznaczenia kąta skręcenia układu tłowego względem układu pikselowego i przesunięcia
pomiędzy początkiem układu pikselowego, który znajduje się w lewym górnym narożniku
obrazu a początkiem układu tłowego, który znajduje się w punkcie głównym zdjęcia
(rys.1.1.). Do wyznaczenia kąta skręcenia potrzebne są, co najmniej dwa punkty
dostosowania, a do wyznaczenia przesunięcia początków układów, co najmniej jeden. Tymi
punktami dostosowania są znaczki tłowe odfotografowane na zdjęciu. W czasie kalibracji

kamery wyznaczane są współrzędne znaczków tłowych w układzie tłowym. Pomierzone na
obrazie cyfrowym współrzędne pikselowe znaczków tłowych oraz znane z kalibracji
współrzędne w układzie tłowym umożliwiają dokonani transformacji z układu pikselowego
do układu tłowego.

Przy okazji orientacji wewnętrznej można poprawić również błędy skurczu filmu

powstałe w czasie pomiędzy wykonaniem zdjęcia a jego zeskanowaniem. Proces
wywoływania zdjęć i późniejszego ich użytkowania może spowodować zniekształcenia filmu.
Korzystając z tego, że na zdjęciu odfotografują się minimum cztery znaczki tłowe można
przynajmniej częściowo poprawić skutki tych błędów. Większość analogowych kamer
lotniczych posiada w tej chwili osiem znaczków tłowych (cztery w narożnikach i cztery
w połowie boków ramki tłowej) co umożliwia lepsze usunięcie wpływu skurczu filmu. Do
wprowadzenia skręcenia i przesunięcia układu tłowego względem układu pikselowego
wystarczyłaby transformacja izometryczna (obrót i przesunięcie bez zmiany skali). Ze
względu na konieczność zmniejszenia wpływu błędu skurczu filmu stosuje się transformacje:

 Helmerta (równomierna zmiana skali)

 afiniczna (zmian skali o różnym współczynniku wzdłuż obu osi układu)

 biliniowa (umożliwiająca wprowadzenie bardziej skomplikowanych korekt

niż afiniczna)

 rzutowa (wprowadzenie przekształcenia rzutowego)

x

obr

(nr kolumny)

układ obrazu -
pikselowy

układ tłowy

zależność

x

y

y

o

x

o

x

o

y

o

Rys. 1.5. Zasada orientacji wewnętrznej zeskanowanego analogowego zdjęcia w autografie cyfrowym

Zdjęcia z kamery cyfrowej

Zdjęcia z kamery cyfrowej nie posiadają błędów wywołanych skurczem filmu, bo są

bezpośrednio rejestrowane na matrycy w kamerze. Ramkę zdjęcia (tłową) stanowi ramka
matrycy tak, więc układ tłowy jest równoległy do układu pikselowego (rys. 1.6). Pozostaje,
więc jedynie potrzeba przesunięcia początku układu z lewego górnego narożnika do punktu
głównego zdjęcia. W czasie kalibracji kamery wyznaczane jest położenie punktu głównego
zdjęcia i jest ono podawane bądź w odniesieniu do lewego górnego narożnika, bądź tez

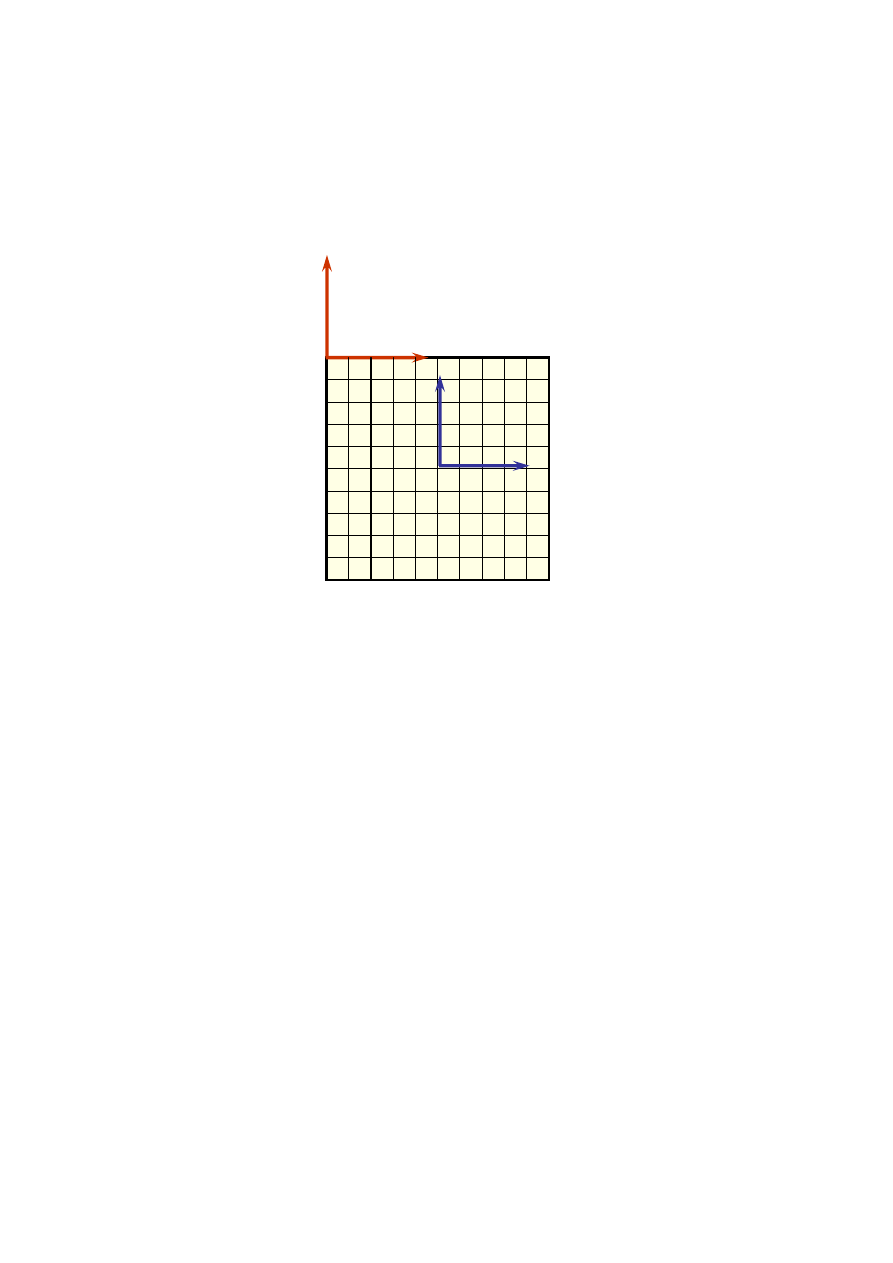
w odniesieniu do środka obrazu. Do dokonania w autografie orientacji wewnętrznej zdjęć
z kamery cyfrowej wystarczy, więc podanie położenia punktu głównego oraz rozmiaru
piksela matrycy w mm. W niektórych starszych programach do wykonania orientacji
wewnętrznej konieczny jest pomiar punktów dostosowania, którymi z powodu braku
znaczków tłowych są narożniki obrazu.

x

obr

(nr kolumny)

y

obr

(nr wiersza)

x

y

Rys. 1.6. Zasada orientacji wewnętrznej zdjęcia z kamery cyfrowej w autografie cyfrowym

1.4.2. Orientacja wzajemna zdjęć w autografie cyfrowym

W orientacji wzajemnej dążymy do odtworzenia wzajemnego położenia względem siebie

pary zdjęć stanowiących stereogram. Jeżeli to wzajemne położenie zdjęć zostanie odtworzone
to promienie jednoimienne (czyli poprowadzone z obu środków rzutów przez obrazy tego
samego punktu na zdjęciach) powinny się przecinać. Prowadzi to do powstania modelu
terenu, ale o nieznanej skali i o nieznanej orientacji względem terenowego układu
współrzędnych. Model ten jednak wewnętrznie jest prawidłowy tzn., że wzajemne proporcje
odległości pomiędzy dowolnymi punktami modelu (z włączeniem środków rzutów zdjęć)
i wartości kątów pomiędzy dowolnymi kierunkami są prawidłowe. Miernikiem przecięcia się
promieni jednoimiennych jest tzw. paralaksa poprzeczna.

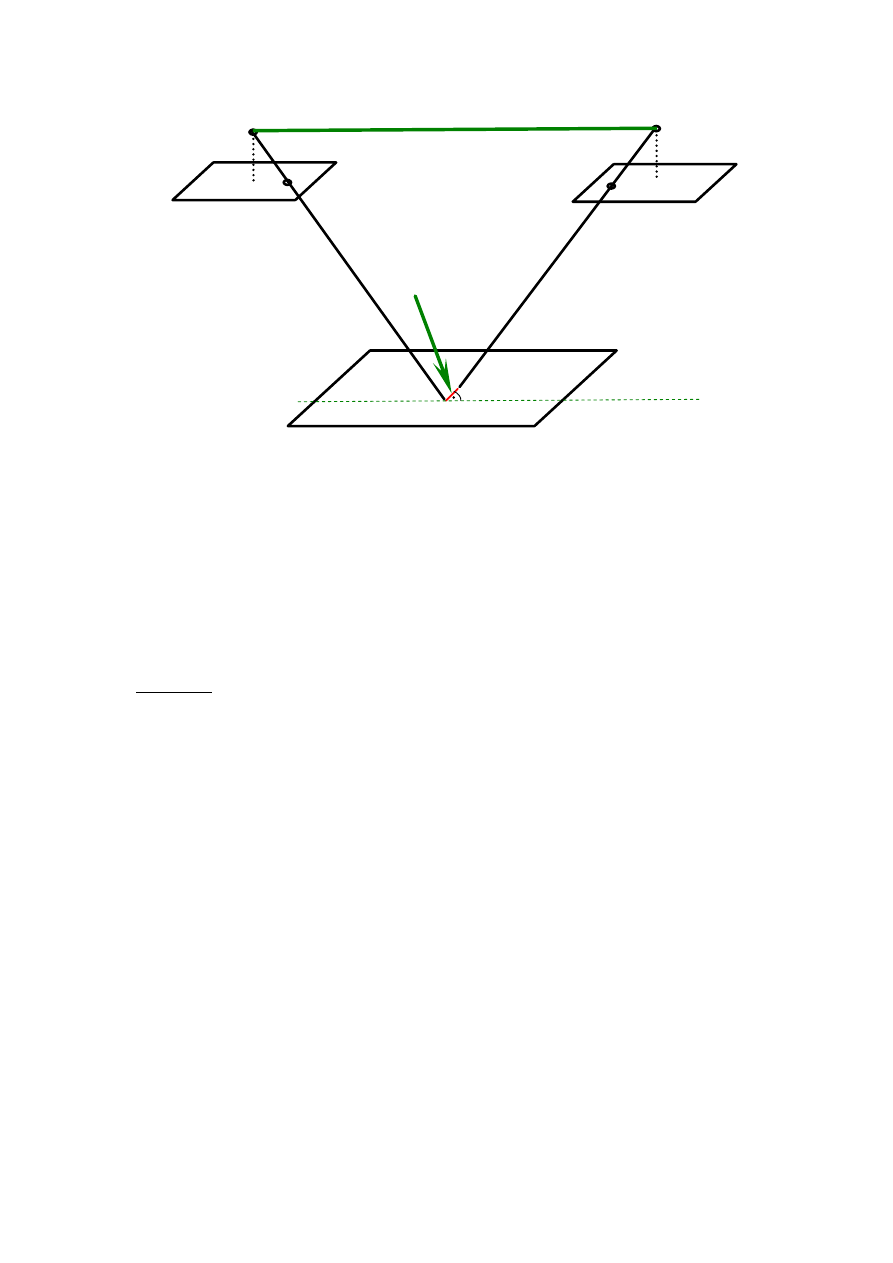
linia równoległa
do bazy zdjęć

paralaksa
poprzeczna

Rys. 1.7. Paralaksa poprzeczna

Ponieważ dane do wykonania orientacji wzajemnej pochodzą z pomiaru nie jest możliwe

idealne przecinanie się wszystkich promieni. Przeważnie przyjmuje się wówczas, że punkt
modelu leży w połowie odcinka najmniejszej odległości pomiędzy odpowiadającymi sobie
promieniami. W efekcie miernikiem jakości wykonania orientacji wzajemnej będzie wielkość
szczątkowej paralaksy poprzecznej. Przyjmuje się, że przy dobrej jakości zdjęć szczątkowa
paralaksa poprzeczna nie powinna przekroczyć 0.5 piksela.

Istnieją dwie metody wykonania orientacji wzajemnej: kątowa i kątowo -liniowa.

Opiszemy tutaj metodę kątowo-liniową. Zasadę wykonania orientacji wzajemnej opisać
można korzystając z równania kolinearności (1.2).

Założenia:

 Przyjmujemy układ współrzędnych modelu (x

m

, y

m

, z

m

) w ten sposób, że zaczepiamy go

w lewym środku rzutów i oś z

m

pokrywa się z osią kamery lewego zdjęcia (rys.1.8).

 W tak zdefiniowanym układzie lewy środek rzutów ma współrzędne x

m

’=0, y

m

’=0,

z

m

’=0. W związku z tym współrzędne prawego środka rzutów w układzie modelu

będą wynosić x

m

”=b

x

, y

m

”=b

y

, z

m

”=b

z

. Zmiana wszystkich wartości b

x

, b

y

, b

z

w

jednakowej proporcji powoduje jedynie zmianę skali modelu (prawy środek rzutów
przesuwa się wówczas po linii bazy). Możliwość zmiany wszystkich trzech
składowych bazy spowodowałaby, że otrzymalibyśmy nieskończoną liczbę
rozwiązań, czyli w zasadzie zadanie stałoby się nie do rozwiązania. Przyjmujemy,
więc że w czasie orientacji wzajemnej będziemy wyznaczać jedynie składowe b

y

, i b

z

a składową bx przyjmujemy o dowolnej wartości i w dalszym ciągu procedury
orientacji wzajemnej nie będziemy jej zmieniać.

 Ponieważ oś z

m

pokrywa się z osią kamery kątowe elementy orientacji lewego zdjęcia

wynoszą

’ = ’ = 0. Orientujemy oś x

m

równolegle do osi x’ układu tłowego

lewego zdjęcia w związku, z czym kąt

’= 0.

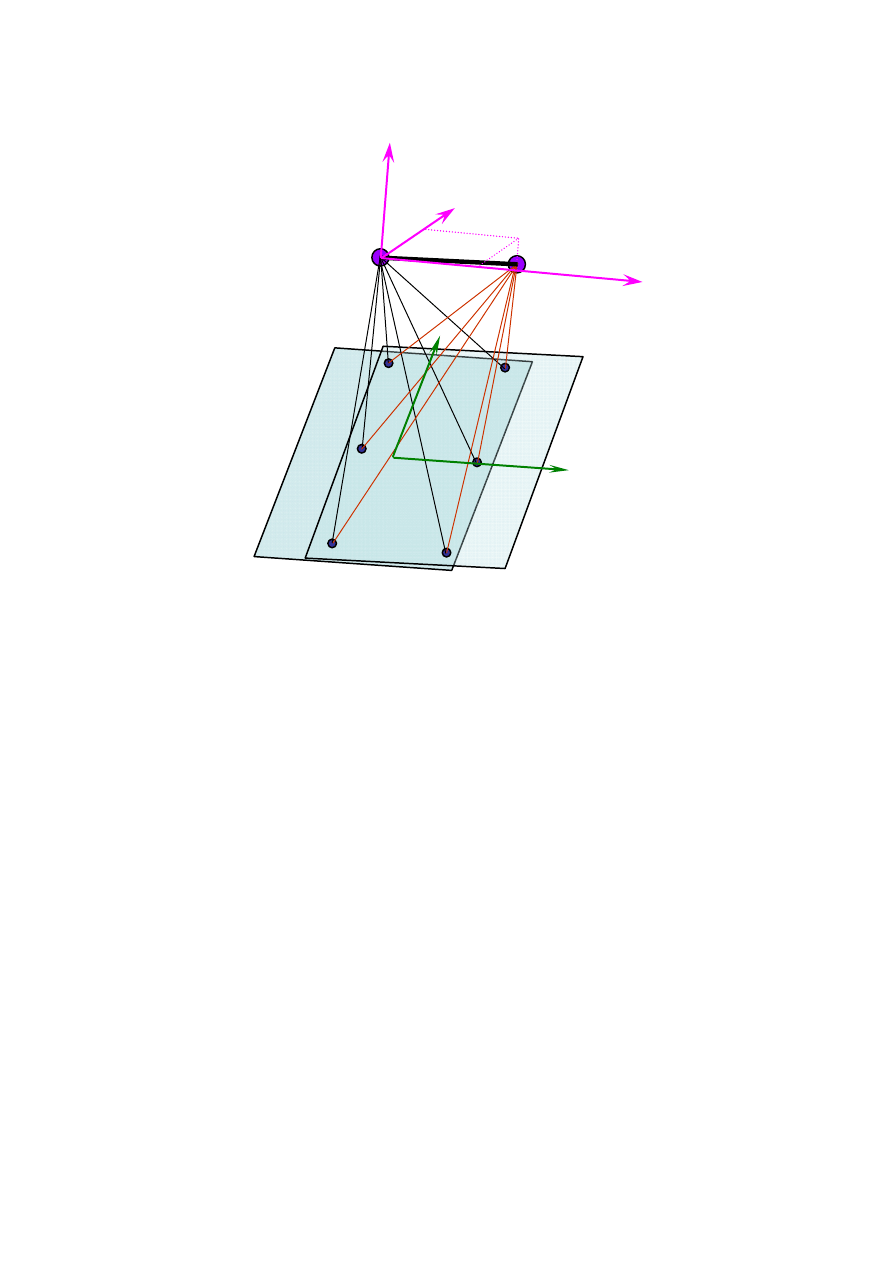
O’

O”

x

m

y

m

z

m

b

x

b

y

b

z

y’

x’

Rys. 1.8. Orientacja wzajemna stereogramu zdjęć fotogrametrycznych

Po przyjęciu powyższych założeń dla obu zdjęć znamy wartości siedmiu elementów

orientacji zdjęć: x

Om

’= 0, y

Om

’= 0, z

Om

’= 0,

’= ’= ’= 0, x

Om

” = b

x

(przyjęta dowolnie

wartość). W równaniu kolinearności (1.2) nieznane pozostało, zatem pięć elementów
orientacji prawego zdjęcia:

”, ”, ”, y

Om

”= b

y

, z

Om

”= b

z

(b

y

i b

z

są wartościami

nieznanymi). Wynika Stąd że w omawianej metodzie elementami orientacji wzajemnej są:
”, ”, ”, b

y

, b

z

.

Każdy pomierzony na dwóch zdjęciach punkt umożliwia ułożenie czterech równań

kolinearności. W każdym z tych równań niewiadomymi są trzy współrzędne (w układzie
modelu) pomierzonego punktu i pięć wymieniowych wyżej elementów orientacji wzajemnej
czyli elementów orientacji zewnętrznej prawego zdjęcia (stałą kamery c

k

znamy z kalibracji

kamery). Dla pięciu pomierzonych punktów można ułożyć dwadzieścia równań
z dwudziestoma niewiadomymi, czyli jest to wtedy rozwiązanie jednoznaczne.

We wspomnianej wcześniej metodzie kątowej orientacji wzajemnej inaczej definiuje się

kierunki osi układu współrzędnych modelu i wówczas nieznanymi są dwa elementy orientacji
kątowej lewego zdjęcia

’, ’ (’ = 0) i ”, ”, ” dla prawego zdjęcia,

Ze względu na uwarunkowanie równań mierzone punkty muszą znajdować się w tzw.

rejonach Grubera (rys. 1.9). (oczywiście punkty wykorzystywane do orientacji wzajemnej nie
posiadają znanych współrzędnych terenowych). Ponieważ pięć punktów daje rozwiązanie
jednoznaczne z reguły mierzy się sześć punktów po jednym w każdym rejonie lub dwanaście
po dwa w każdym rejonie.

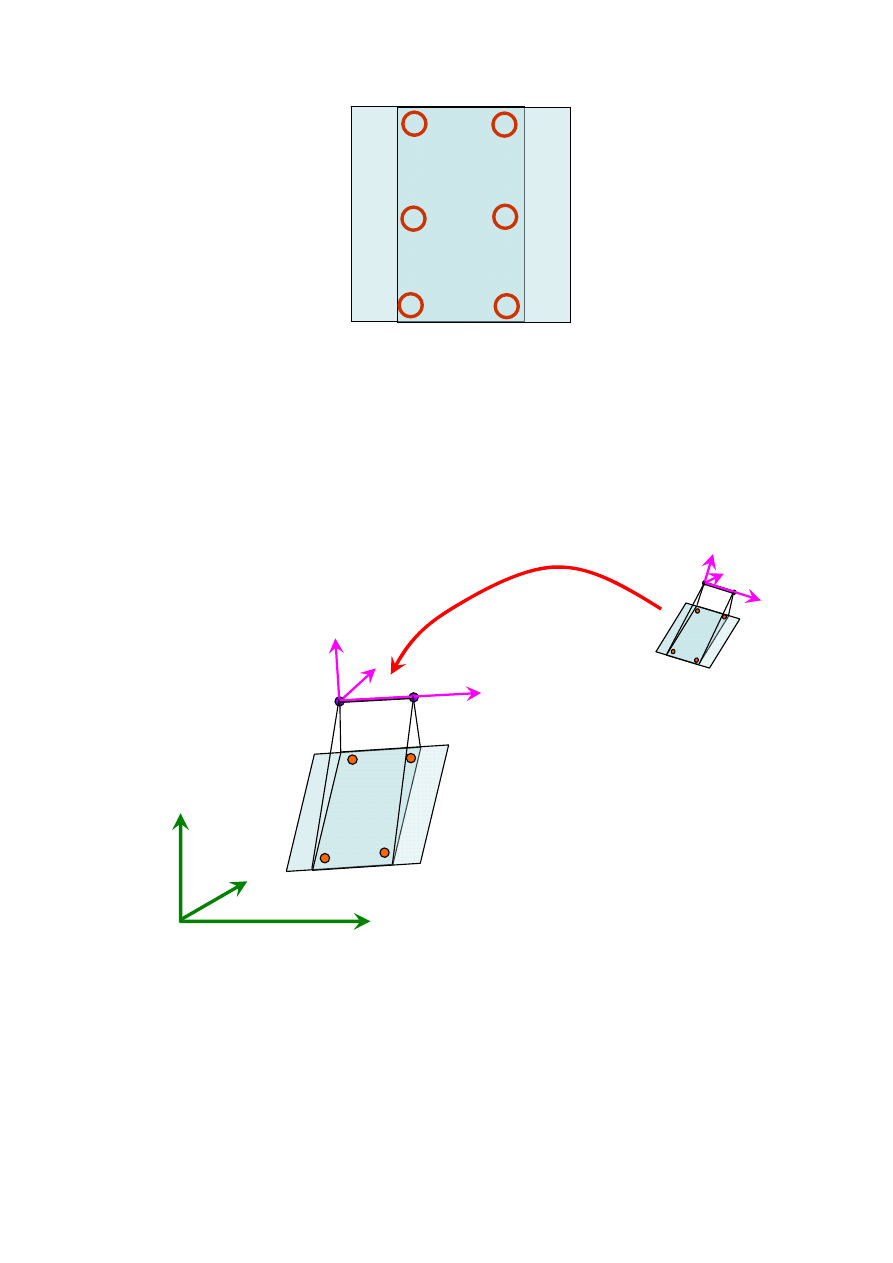
Rys. 1.9. Rejony Grubera

1.4.3. Orientacja bezwzględna zdjęć w autografie cyfrowym

Po wykonaniu orientacji wzajemnej uzyskujemy model, który nie jest w odpowiedniej

skali i ma przypadkową orientację w przestrzeni. Na podstawie punktów dostosowania
(fotopunktów) o znanych współrzędnych terenowych wykonuje się transformację
w przestrzeni trójwymiarowej, która umożliwia przeskalowanie, obrót i „osadzenie” modelu
na fotopunktach (rys.1.10).

Z

Y

X

Rys. 1.10. Orientacja bezwzględna stereogramu w autografie cyfrowym

Fotopunkty mogą być sygnalizowane (rys. 1.11) przed nalotem lub mogą być wyraźnymi

szczegółami terenowymi. Fotopunkty sygnalizowane umożliwiają większą dokładność ich
pomiaru lecz wymagają większego nakładu pracy.

Transformacja w przestrzeni wymaga minimum trzech punktów dostosowania. Ponieważ

dla trzech punktów jest to rozwiązanie jednoznaczne z reguły stosuje się od czterech
(rys.1.10) do sześciu (ułożonych w miarę możliwości podobnie jak punkty do orientacji
wzajemnej).

Rys. 1.11. Sygnalizacja fotopunktów

2. Mapy fotograficzne

W autografie obserwując stereoskopowo stereogram zdjęć lotniczych możemy rysować

mapy, czyli tworzymy mapy wektorowe. Ze zdjęć można również opracować mapy w postaci
fotograficznej, czyli rastrowej.

2.1. Skala zdjęcia lotniczego

Skala pionowego zdjęcia lotniczego terenu płaskiego i poziomego pokazana jest na

rysunku. 2.1 Zdjęcie lotnicze zazwyczaj nie może być wykorzystywane bezpośrednio jako
mapa ponieważ ma nierównomierną skalę. Jeżeli teren nie jest płaski to różne fragmenty tego
terenu w zależności od wysokości posiadają na zdjęciu różną skalę (rys. 2.2).

Rysunek 2.3 pokazuje sytuację, która nastąpiłaby gdybyśmy wykonali mapę przez

powiększenie zdjęcia przyjmując, jako poziom odniesienia do wyznaczenia skali mapy
wysokość punktu A. Na tej mapie punkt B odwzorowałby się w punkcie B

s

zamiast

w punkcie B

0

. Błąd na mapie określa odcinek

s a jego odpowiednik na zdjęciu to odcinek

r. Ponieważ odchyłka ta ma kierunek po promieniu od punktu głównego zdjęcia nosi nazwę
odchyłki radialnej. Jak widać

r wzrasta wraz z oddalaniem się od punktu głównego zdjęcia

i wraz ze wzrostem

h, maleje natomiast ze wzrostem wysokości lotu W.

Nachylenie zdjęcia również powoduje jego nierównomierną skalę (rys. 2.4).

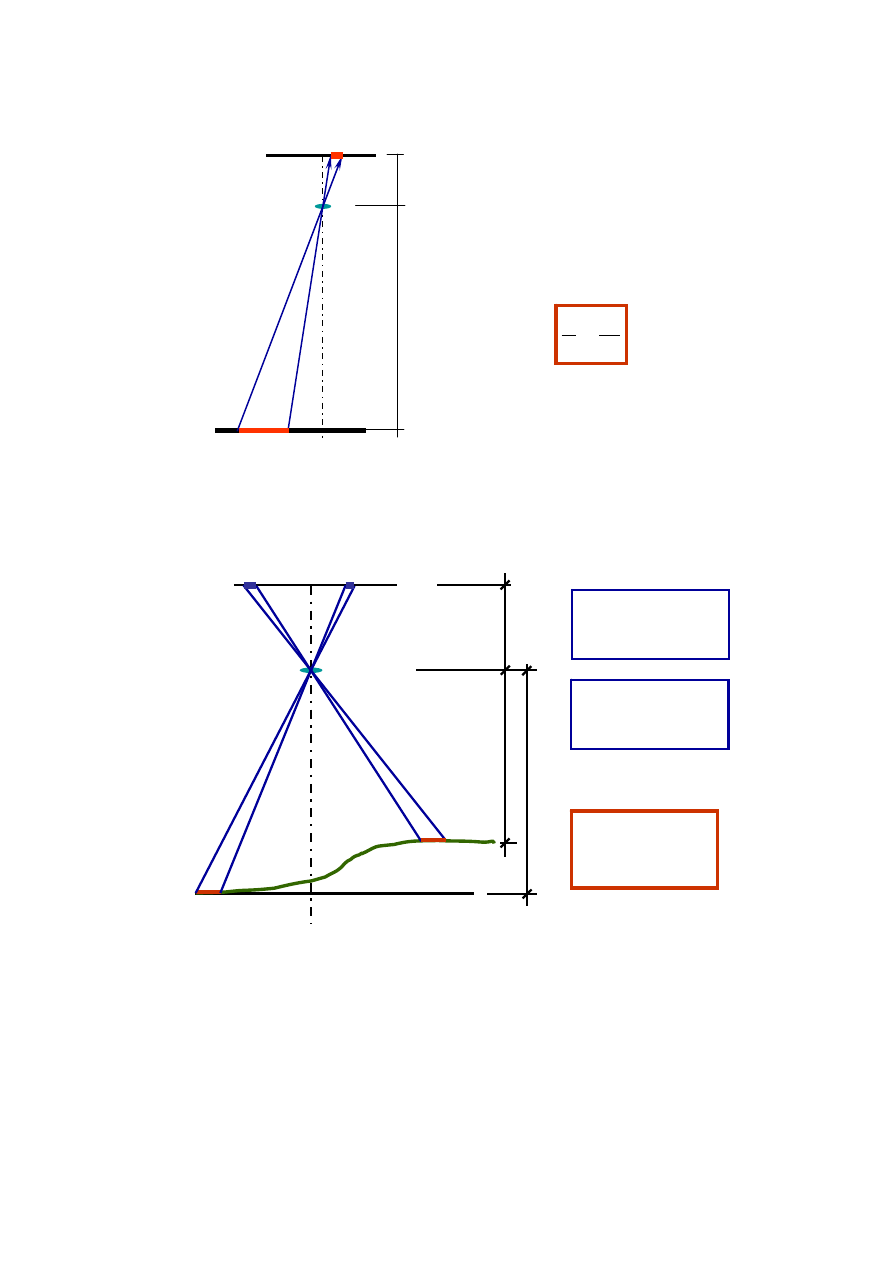
y = c

k

x = W

L

l

skala zdjęcia lotniczego

1 : m

z

wynosi:

W

c

L

l

k



Rys. 2.1. Skala pionowego zdjęcia lotniczego terenu płaskiego i poziomego

a

a

b

b

c

w

w

a

skala odcinka a
a’:a = c

k

:w

a

skala odcinka b
b’:b = c

k

:w

b

w

a

 w

b



(a’:a)

 (b’:b)

Rys. 2.2. Skala pionowego zdjęcia lotniczego terenu o zróżnicowanych wysokościach

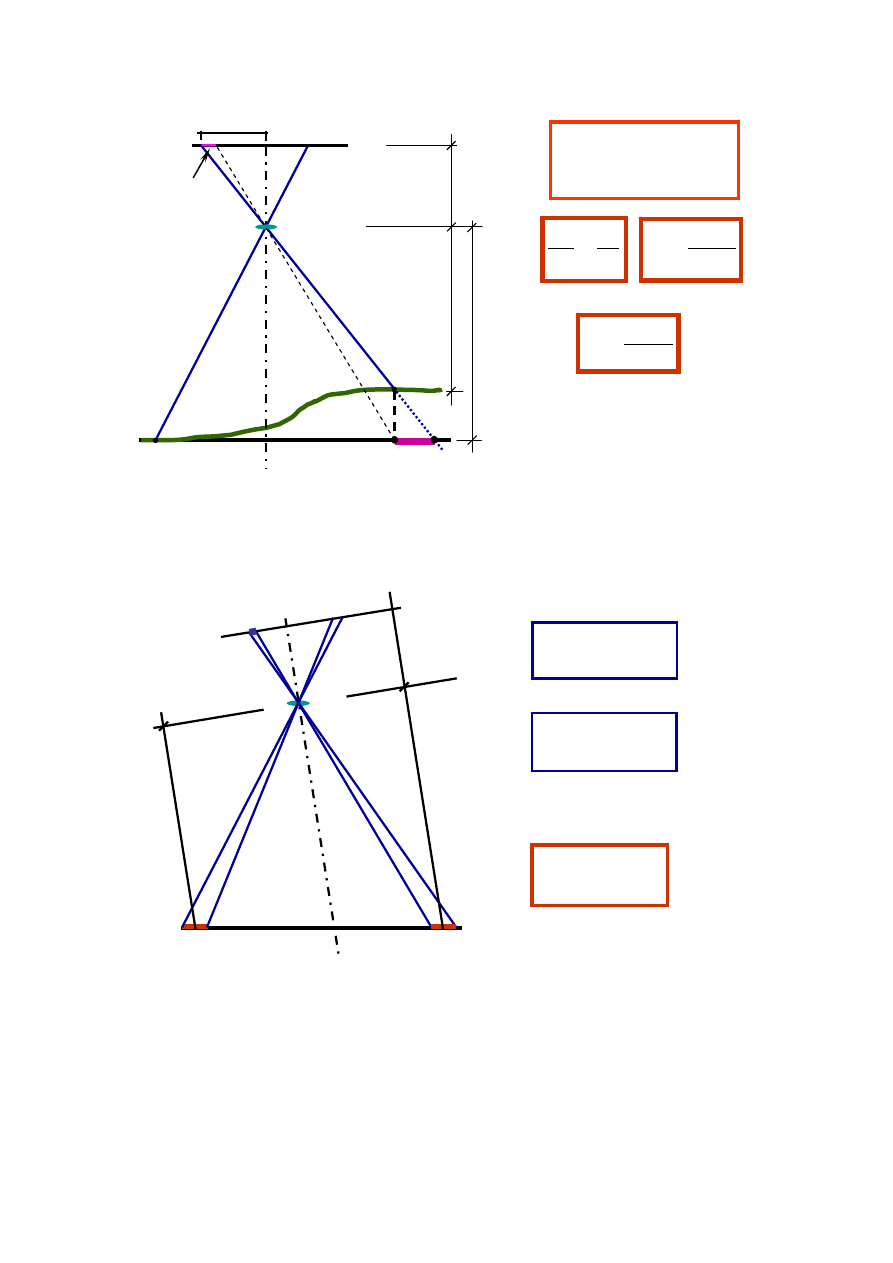
c

k

w

b

w

a

A

B

punkt A definiuje poziom
odniesienia

s

k

c

r

h

s 





k

c

r

h

=

s







s

- błąd na mapie

spowodowany
deniwelacją terenu

r

h

B

0

B

s

r

W

h

=

r

r







Rys. 2.3. Odchyłka radialna spowodowana deniwelacją terenu

a

a’

b

b’

c

k

w

b

w

a

skala odcinka a
a’:a = c

k

:w

a

skala odcinka b
b’:b = c

k

:w

b

w

a

 w

b



(a’:a)

 (b’:b)

Rys. 2.4. Wpływ nachylenia zdjęcia na jego skalę

2.2. Opracowanie fotomapy za pomocą przekształcenia rzutowego

Przekształcenie rzutowe umożliwia przekształcenie płaszczyzny punktów w inną

płaszczyznę punktów przy założeniu, że odpowiadające sobie punkty leżą na promieniach
wychodzących z jednego punktu (rys. 2.5). Taki zbiór promieni nazywamy pękiem.

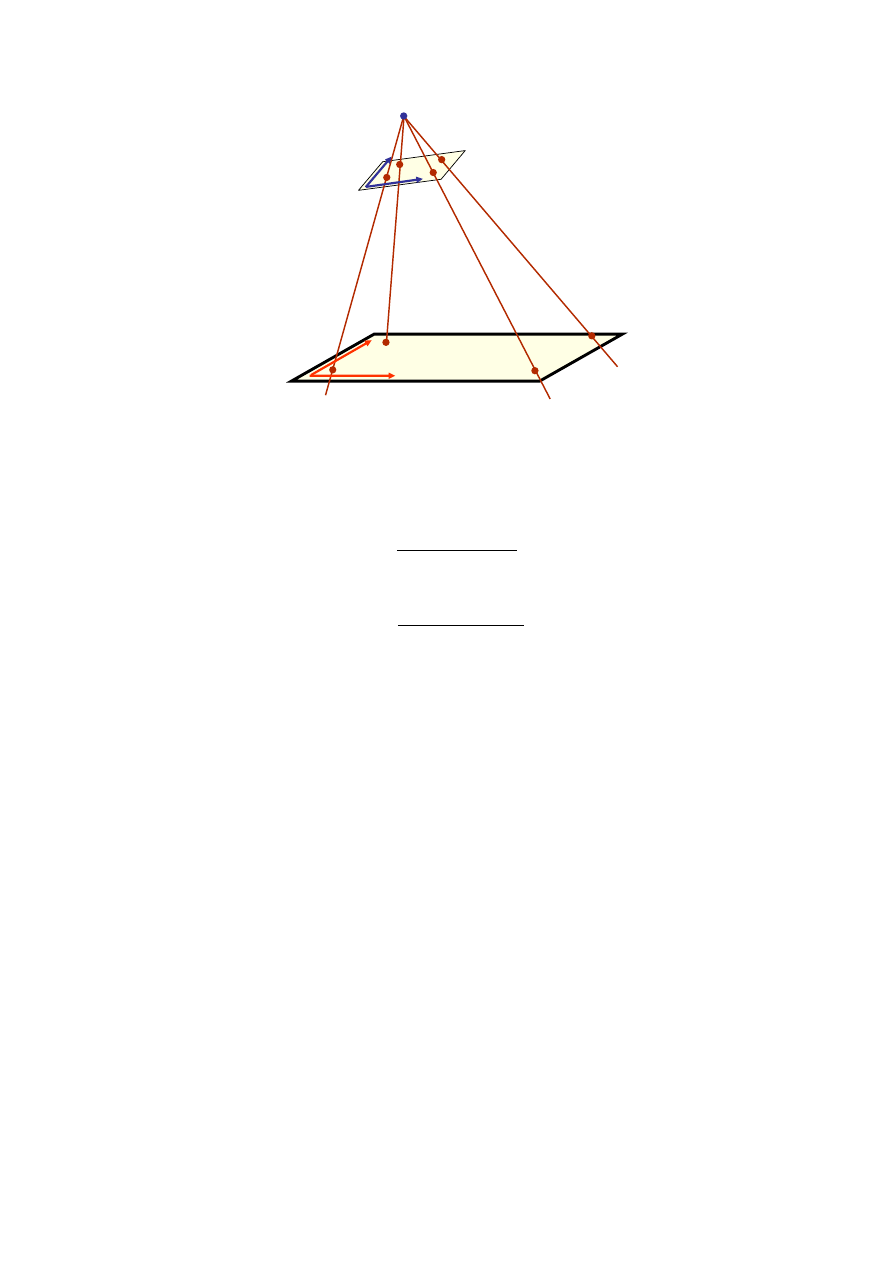
x

y

Y

X

Rys. 2.5.Przekształcenie rzutowe płaszczyzny na płaszczyznę

Na każdej z płaszczyzn możemy zdefiniować dowolny układ współrzędnych. Zależność

pomiędzy współrzędnymi odpowiadających sobie punktów podaje wzór:

1

1





































Y

E

X

D

H

Y

G

X

F

y

Y

E

X

D

C

Y

B

X

A

x

(2.1)

Przekształcając zdjęcie nachylone możemy w ten sposób usunąć wpływ jego nachylenia.

Aby po przekształceniu zdjęcia można było uzyskać mapę odpowiadającą terenowi
odfotografowanemu na zdjęciu musi być spełniony warunek, że teren da się przekształcić
rzutowo na zdjęcie. Przekształcenie to możemy zastosować jednak tylko wtedy, gdy
przekształcamy płaszczyznę na płaszczyznę. W związku z tym przekształcenie rzutowe
możemy wykonywać jedynie wtedy, gdy teren jest płaszczyzną.

W praktyce wystarczy, że teren jest w przybliżeniu płaszczyzną. Mapa jest, bowiem

opracowywana z określoną dokładnością. Jeżeli błędy spowodowane deniwelacją terenu nie
przekroczą dozwolonej wielkości błędu mapy to można do opracowania fotomapy ze zdjęcia
lotniczego wykorzystać przekształcenie rzutowe (rys. 2.6). W chwili obecnej przekształcenia
rzutowego do opracowywania map ze zdjęć lotniczych w zasadzie się nie wykorzystuje.
Korzysta się natomiast z tej metody opracowując fotoplany elewacji ścian czy też fotoplany
malowideł w fotogrametrycznej inwentaryzacji obiektów architektonicznych.

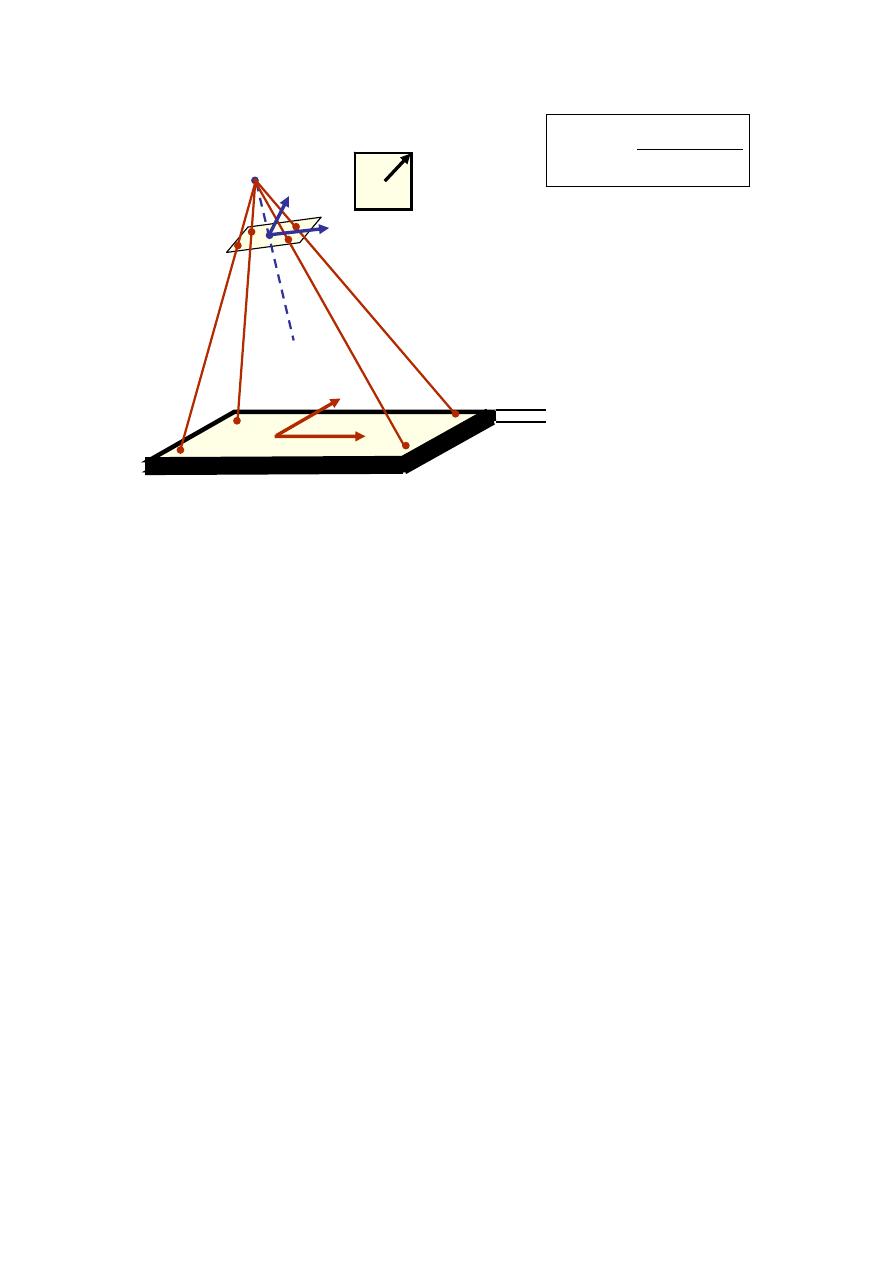
max

max

max

r

c

R

h

k









r

max

< 2Δh

max

(maksymalna różnica
wysokości terenu)

x

y

X

Y

przyjmując płaszczyznę odniesienia w

środku grubości plastra możemy mieć

grubość plastra równą ± Δh

max

R

max

jest to dozwolony błąd w terenie

wynikający z dozwolonego błędu na mapie

Rys. 2.6. Przekształcenie rzutowe terenu prawie płaskiego na zdjęcie

2.3. Opracowanie ortofotomapy

Ortofotografia umożliwia przekształcenie obrazu zdjęcia w mapę usuwając nie tylko

wpływ nachylenia zdjęcia, ale też błędy spowodowane deniwelacją terenu. Omówimy tutaj
zasadę przekształcenia ortofotograficznego tzw. metodą odwrotną.

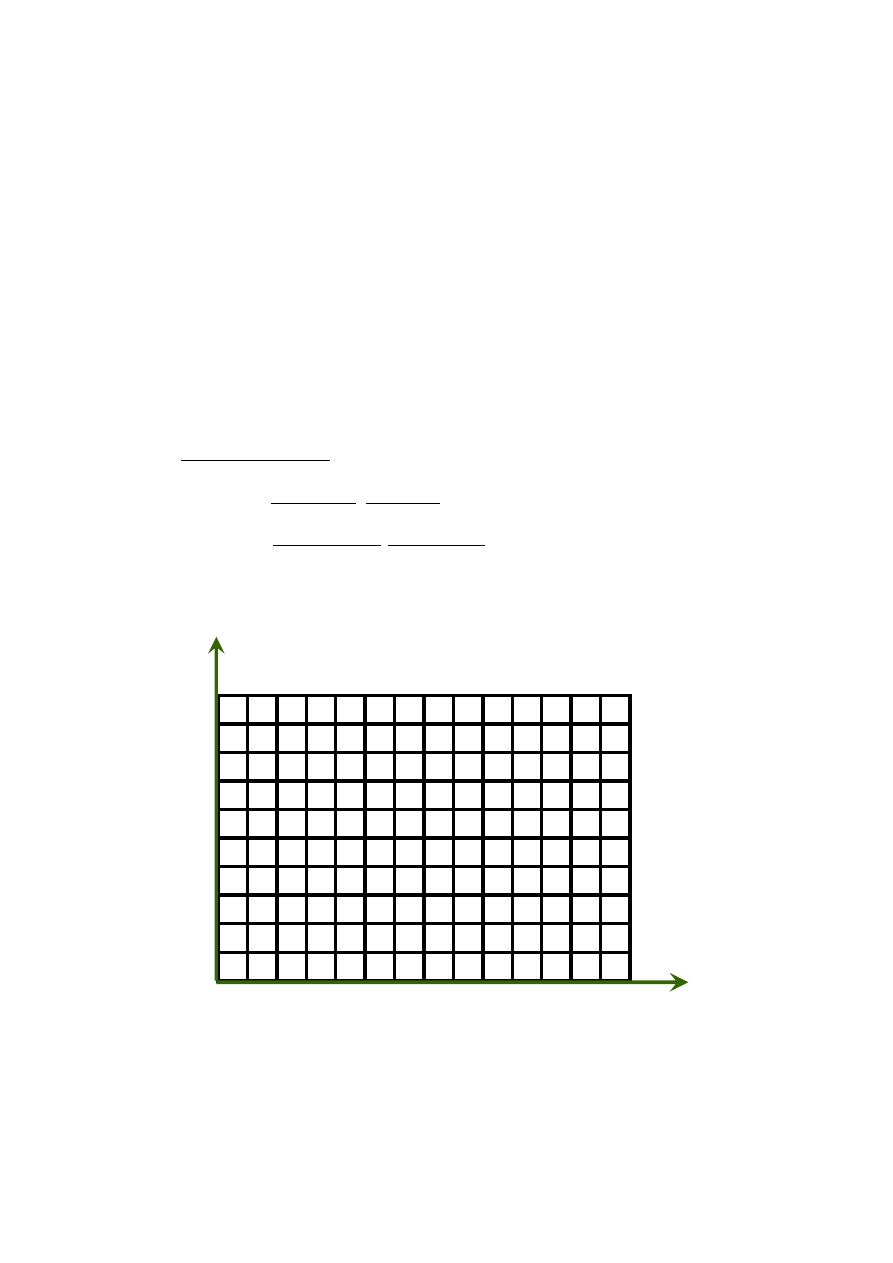
Wyobraźmy sobie pustą cyfrową ortofotomapę (rys. 2.7). Pusta jeszcze ortofotomapa (tak

jak pusta jeszcze mapa kreskowa) ma przyporządkowany układ współrzędnych (posiada
georeferencje tzn. jest przyporządkowana do określonego miejsca w przestrzeni). Pusta
ortofotomapa cyfrowa jest już podzielona na poszczególne piksele, środki pikseli mają
w związku z tym znane współrzędne w układzie, w którym ortofotomapa ma być
sporządzona. Piksele te nie mają jeszcze przydzielonej jasności (ortofotomapa w tonacji
szarości) lub też barwy (ortofotomapa barwna). Tą jasność (barwę) trzeba pobrać
z odpowiedniego piksela zdjęcia. Ale, z którego piksela? Odpowiedź na to pytanie próbuje
wyjaśnić poniższy komentarz i rysunek 2.8.

Zdjęcie, które przekształcamy na ortofotomapę musi mieć znane elementy orientacji

zewnętrznej i

elementy orientacji wewnętrznej. Przebieg przekształcenia wyględa

następująco:

 Środek pustego piksela ortofotomapy ma znane współrzędne płaskie X, Y nie jest

znana natomiast współrzędna wysokościowa Z, bo ortofotomapa jest mapą płaską
tylko w układzie XY. Dlatego konieczny jest numeryczny model terenu (NMT),
z którego odczytana zostanie wysokość Z punktu terenowego odpowiadającego
współrzędnym X, Y.

 Mając współrzędne X, Y, Z punktu terenowego (odpowiadającego pikselowi

ortofotomapy) należy wyznaczyć z równania kolinearności (1.2) współrzędne
tłowe x, y odpowiadającego mu punktu na zdjęciu. Ponieważ znane są elementy
orientacji zewnętrznej zdjęcia (X

O

, Y

O

, Z

O

– współrzędne środka rzutów; kąty

obrotu zdjęcia -

, , ; stała kamery c

k

; położenie punktu głównego na zdjęciu)

z równania (1.2) można w prosty sposób wyliczyć współrzędne tłowe po
podstawieniu w

równaniu współrzędnych środka piksela X, Y, Z jako

współrzędne X

P

, Y

P

, Z

P

. Po obliczeniu współrzędnych tłowych x, y należy

obliczyć współrzędne pikselowe. Można to uczynić gdyż na początku całego
procesu przetwarzania wykonuje się procedurę orientacji wewnętrznej, czyli
znana jest zależność pomiędzy układem tłowym i obrazowym zdjęcia.

 W ten sposób znajdujemy piksel zdjęcia, który odpowiada analizowanemu pikselowi

ortofotomapy i z tego piksela na zdjęciu pobieramy jasność lub barwę
i przydzielamy pikselowi ortofotomapy.

 Procedurę powyższą powtarzamy kolejno dla wszystkich pikseli ortofotomapy.

Przy przydzielaniu jasności pikselowi ortofotomapy pojawia się problem, że środkowi

piksela ortofotomapy z reguły nie odpowiada środek piksela zdjęcia, ale jakiś inny punkt na
tym pikselu. Można wówczas jasność (barwę) potrzebną do przydzielenia pikselowi
ortofotomapy interpolować biorąc pod uwagę także sąsiednie piksele zdjęcia. Powszechnie są
stosowane trzy metody takiej interpolacji:



najbliższego sąsiada - jeżeli takowej interpolacji nie wykonujemy, lecz bierzemy

jasność piksela, na który trafił wyliczony punkt



interpolacja dwuliniowa (biliniowa) - bierze pod uwagę jasność czterech sąsiednich

pikseli



interpolacja dwusześcienna (bisześcienna) - biorąca pod uwagę jasność szesnastu

sąsiednich pikseli

X

Y

? ?

?

? ? ?

Rys. 2.7. „Pusta” ortofotomapa

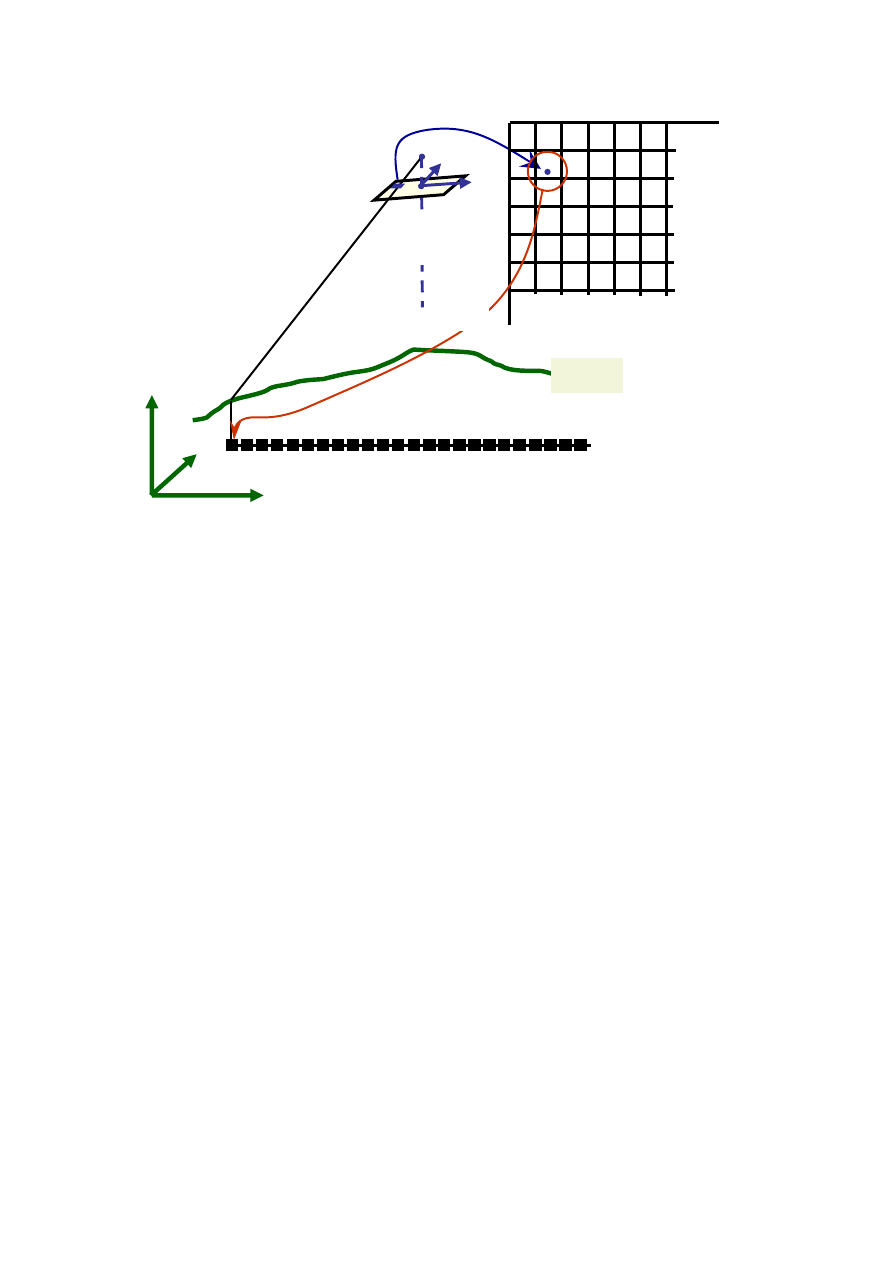
NMT

ortofotomapa

fragment
zdjęcia

(układ pikseli)

X

Z

Y

x

y

X,Y

X,Y,Z

x, y tłowe – równanie

kolinearności

znane

elementy

orientacji

jasność
(barwa)

Rys. 2.8. Zasada przekształcenia ortofotograficznego

Reasumując, aby wykonać przetwarzanie ortofotograficzne musimy posiadać:



zdjęcie, dla którego musimy mieć znane elementy orientacji wewnętrznej (stała
c

k

, położenie punktu głównego)



elementy orientacji zewnętrznej zdjęcia (jeżeli nie są znane to minimum trzy
fotopunkty na podstawie których można je wyznaczyć)



numeryczny model terenu

Po przekształceniu pojedynczego zdjęcia otrzymuje się ortoobraz, który jest częścią

planowanej ortofotomapy. Po uzyskaniu większej liczby ortoobrazów należy je ze sobą
połączyć (zmozaikować). Sąsiednie ortoobrazy nakładają się częściowo na siebie. Wyznacza
się, więc w pasie zakładki linię cięcia tak, aby w miarę możności nie przechodziła w poprzek
wyraźnych szczegółów (aby była później mniej widoczna). Po zmozaikowaniu kilku
ortoobrazów wycina się z nich fragment odpowiadający arkuszowi mapy. Cechą
charakterystyczną zarówno ortoobrazów jak i wyciętych arkuszy jest fakt posiadania przez
nich tzw. georeferencji. Oznacza to, iż w nagłówku pliku z obrazem lub w osobnym pliku
podana jest informacja o współrzędnych narożników obrazu i o wielkości piksela terenowego.

Klasycznie opracowana ortofotomapa jest to sprowadzony do jednolitej skali obraz

zdjęcia, z którego usunięto zniekształcenia związane z deniwelacją terenu, natomiast nie są
poprawione błędy obrazu elementów wystających ponad teren. Czyli obraz powierzchni
obiektów wystających ponad teren posiada tzw. szczątkowe przesunięcia radialne (rys. 2.9).

Stosowane są też takie metody opracowania ortofotomap, że szczątkowe przesunięcia

radialne obiektów wystających ponad teren są z obrazu usuwane. Metody te noszą nazwę
„true-ortofotografia” (prawdziwa ortofotografia). Są one drogie i wymagają wykonania zdjęć
lotniczych o większym niż standardowe pokryciu podłużnym zdjęć i poprzecznym pomiędzy
szeregami.

Rys. 2.9. Ortofotomapa - szczątkowe przesunięcia radialne elementów wystających ponad powierzchnię

terenu

3. Aerotriangulacja

Wiele metod fotogrametrycznego opracowania zdjęć (np. opracowanie zdjęć na

autografie, ortofotografia) wymaga znajomości elementów orientacji zewnętrznej zdjęć lub
znajomości fotopunktów, czyli punktów na zdjęciu o znanych współrzędnych terenowych.
Fotopunkty można uzyskać przez pomiar w terenie wybranych szczegółów zdjęcia lub
punktów sygnalizowanych przed nalotem. Jeżeli dotyczy to obszaru pokrytego dużą liczbą
zdjęć to liczba fotopunktów do pomiaru byłaby bardzo duża (np. na jeden stereogram z reguły
stosuje się od czterech do sześciu fotopunktów).

Dla zmniejszenia ilości prac terenowych wykonuje się wówczas tzw. aerotriangulację.

Jest to metoda kameralnego wyznaczania współrzędnych pomierzonych na zdjęciach punktów
i wartości elementów orientacji zewnętrznej zdjęć przy wykorzystaniu niewielkiej liczby
pomierzonych w terenie fotopunktów.

Metody wykonywania aerotriangulacji możemy podzielić na analogowe, analityczne

i cyfrowe. W chwili obecnej praktycznie wykonuje się już jedynie aerotriangulacje cyfrową.
W aerotriangulacji analitycznej i cyfrowej stosowano dawniej metodę niezależnych modeli
Natomiast obecnie powszechnie jest stosowana metoda niezależnych wiązek.

Metoda niezależnych modeli polega na łączeniu dwóch sąsiednich zdjęć w modele

a następnie połączeniu modeli w jeden blok. Metoda niezależnych wiązek polega na łączeniu
w blok pojedynczych zdjęć (zdjęcie jest to wiązka promieni) (rys. 3.1).

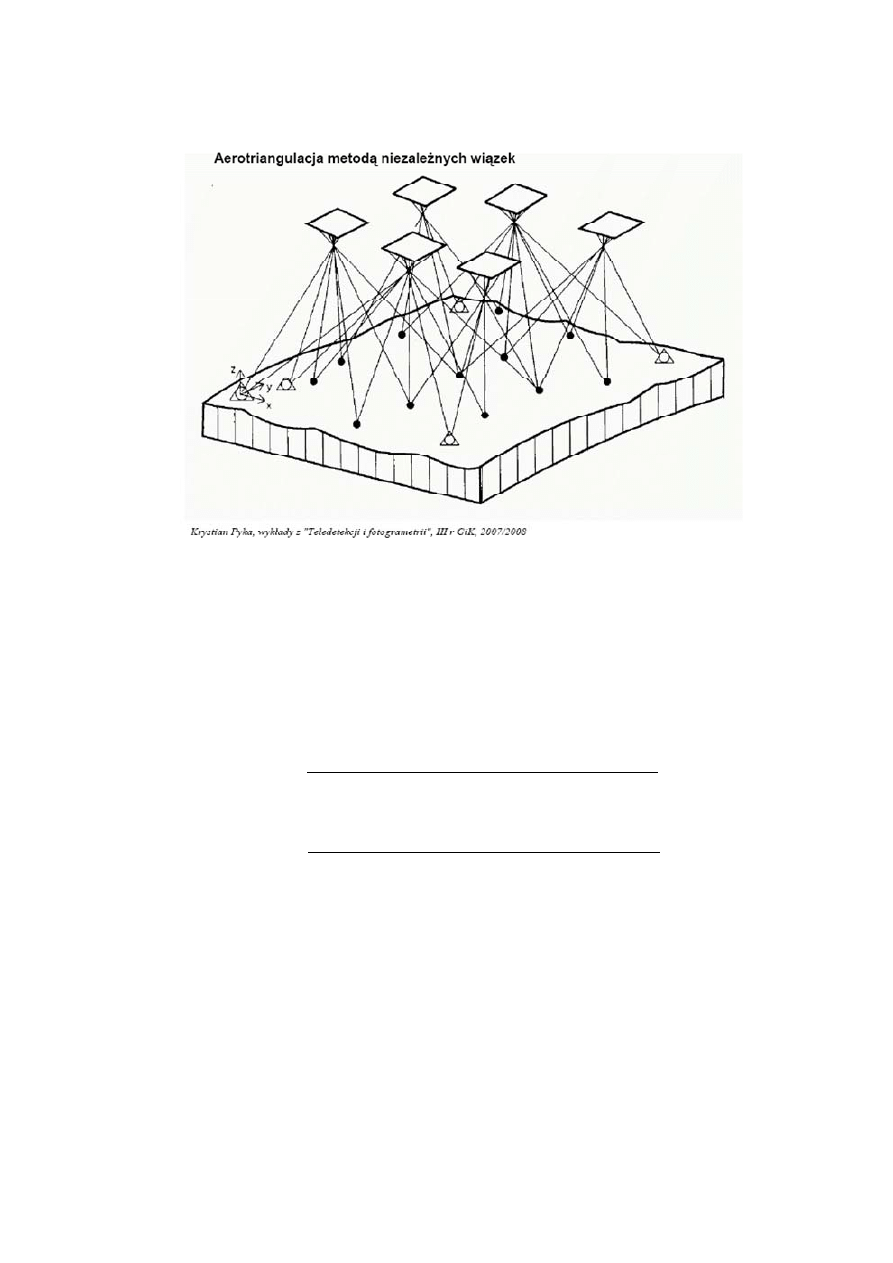
Rys. 3.1 Aerotriangulacja metodą niezależnych wiązek

W metodzie niezależnych wiązek mierzy na zdjęciach oprócz pewnej liczby fotopunktów

dużą liczbę tzw. punktów wiążących (rys. 3.2). Punkty wiążące są to takie punkty, które
pomierzono na co najmniej dwóch zdjęciach, ale nie mają znanych współrzędnych
terenowych.

Dla wszystkich pomierzonych punktów układane są równania obserwacyjne oparte na

równaniu kolinearności (1.2).

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

33

23

13

32

22

12

33

23

13

31

21

11

O

P

O

P

O

P

O

P

O

P

O

P

k

P

O

P

O

P

O

P

O

P

O

P

O

P

k

P

Z

Z

a

Y

Y

a

X

X

a

Z

Z

a

Y

Y

a

X

X

a

c

y

Z

Z

a

Y

Y

a

X

X

a

Z

Z

a

Y

Y

a

X

X

a

c

x













































































(1.2)

Dla jednego punktu wiążącego można ułożyć dwa równania (1.2). Znane są w nich tylko

c

k

i x, y pomierzone na zdjęciu. a liczba niewiadomych wynosi dziewięć. Sześć

niewiadomych związane jest ze zdjęciem – są to elementy orientacji zewnętrznej zdjęcia (X

O

,

Y

O

, Z

O

,

, , ) trzy niewiadome są to nieznane współrzędne terenowe X

P

, Y

P

, Z

P

punktu

wiążącego. Jeden punkt wiążący w zależności od położenia (rys. 3.2) może być pomierzony
na dwóch do sześciu zdjęciach. Na jednym zdjęciu mierzy się co najmniej sześć punktów
wiążących.

W równaniu kolinearności dla fotopunktu jest sześć elementówznanych: c

k

i x, y

pomierzone na zdjęciu oraz współrzędne terenowe X

P

, Y

P

, Z

P

Pozostaje, więc tylko sześć

niewiadomych. (elementy orientacji zewnętrznej zdjęcia). Jeden fotopunkt może być
pomierzony na co najmniej dwóch zdjęciach a maksymalnie na sześciu

Dla przykładowego maleńkiego bloku złożonego z dwunastu zdjęć pokazanego na

rysunku 3.2 liczba równań i niewiadomych przedstawia się następująco:

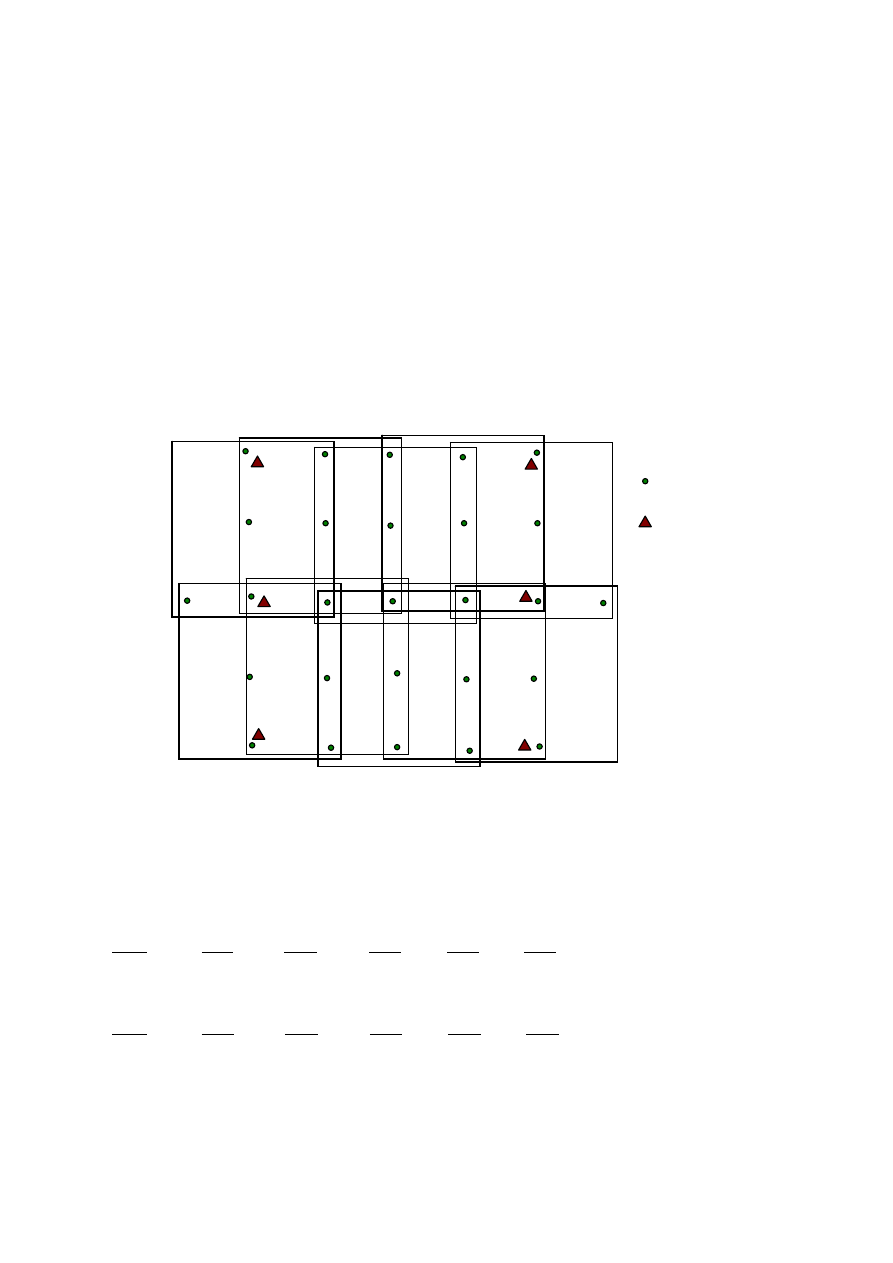
 liczba punktów wiążących = 27 w tym:

o

10 - pomierzonych na dwóch zdjęciach

o

14 - pomierzonych na trzech zdjęciach

o

3 - pomierzone na sześciu zdjęciach

 liczba fotopunktów = 6 w tym:

o

4 - pomierzone na dwóch zdjęciach

o

2 - pomierzone na trzech zdjęciach

Dla punktów wiążących ułożone zostanie (2

(210 + 314 + 63)) 160 równań a dla

fotopunktów 28 równań. Razem będą, więc 182 równania.

W równaniach dla fotopunktów i dla punktów wiążących będą występować 153

niewiadome (81 – niewiadomych współrzędnych terenowych punktów wiążących i 72
elementy orientacji zewnętrznej dwunastu zdjęć). Pozostanie, więc 29 równań nadmiarowych,
co pozwoli rozwiązać cały układ z wyrównaniem. Przy obliczeniach dużych bloków
(kilkadziesiąt do kilkaset zdjęć) proporcja liczby równań nadmiarowych do liczby
niewiadomych jest jeszcze bardziej korzystna.

punkty wiążące

fotopunkty

Rys. 3.2. Punkty pomiarowe stosowane w aerotriangulacji

Rozwiązanie układu równań obserwacyjnych opartych na równaniu kolinearności

w aerotriangulacji pociąga za sobą konieczność ich linearyzacji. Występują, bowiem w nich
funkcje trygonometryczne kątowych elementów orientacji zewnętrznej. Zapis
zlinearyzowanych równań obserwacyjnych przedstawiają równania 3.1

(3.1)

y

zdj

y

y

y

y

y

y

y

x

zdj

x

x

x

x

x

x

x

v

y

F

d

F

d

F

d

F

dZ

Z

F

dY

Y

F

dX

X

F

v

x

F

d

F

d

F

d

F

dZ

Z

F

dY

Y

F

dX

X

F













































































0

0

0

0

0

0

0

0

0

0

0

0

0

0





























W nowoczesnych kamerach stosowany jest pomiar współrzędnych środków rzutów za

pomocą GPS. Wprowadzenie tych danych do rozwiązania układu równań powoduje, że
potrzebna liczba fotopunktów jeszcze bardziej się zmniejsza.