
Materiały pomocnicze do ćwiczeń z przedmiotu:
Termodynamika techniczna
Rozdział 2
Bilans energii. Pierwsza zasada termodynamiki
mgr inż. Agnieszka Sadłowska-Sałęga

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
9
2 Bilans energii. Pierwsza zasada termodynamiki
2.1 Przemiany termodynamiczne
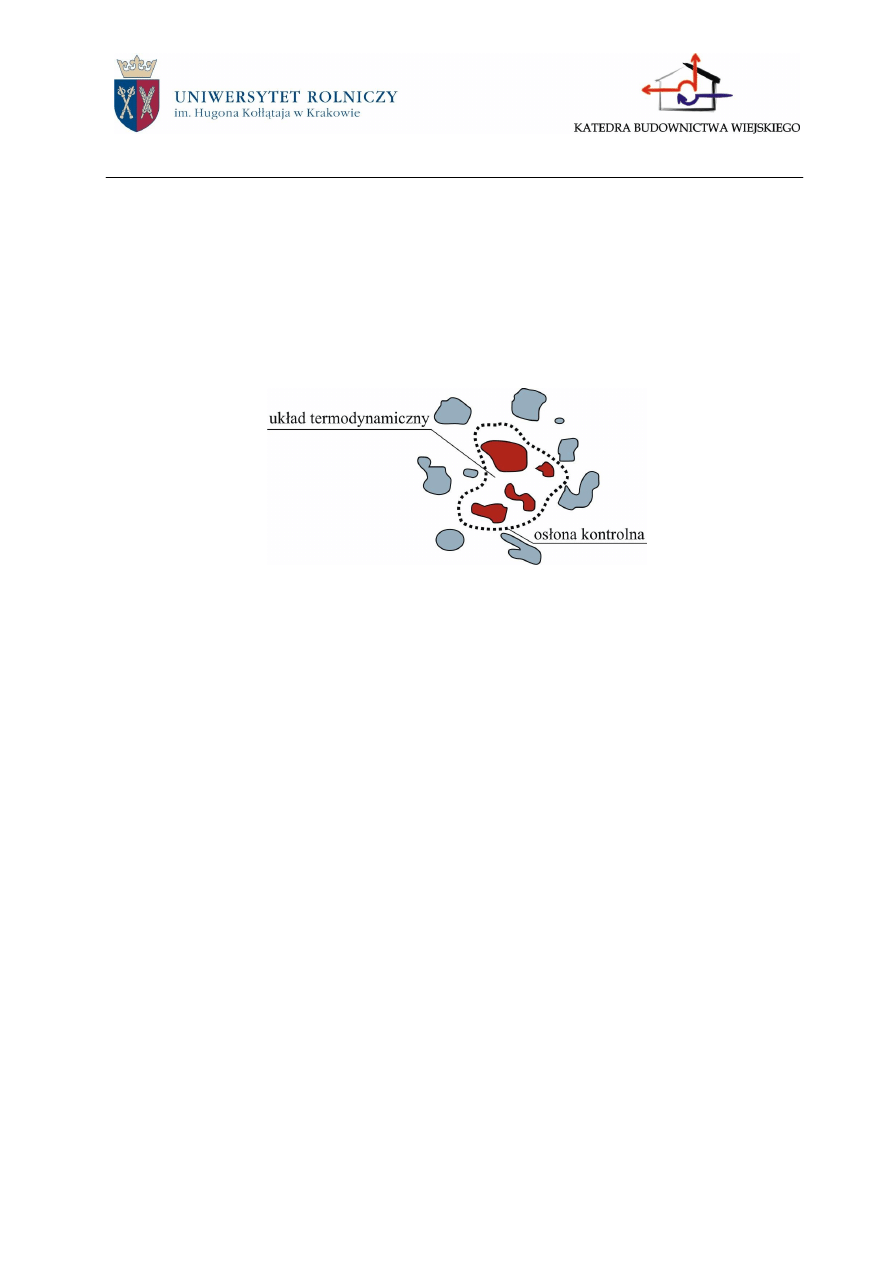
Układ termodynamiczny to dowolnie wybrana część wszechświata, której zachowanie
jest rozpatrywane na podstawie zasad termodynamiki. Pozostały świat to otoczenie termodyna-
miczne.
Rys.2.1. Układ termodynamiczny (wyodrębnienie układu ciał za pomocą osłony kontrolnej)
Dzięki ograniczeniu danego zjawiska do układu można osobno rozpatrywać procesy we-
wnątrz układu i procesy wymiany energii między układem i otoczeniem, o którym dzięki temu
nic nie musimy wiedzieć.
Przemiana termodynamiczna jest to zmiana stanu układu polegająca na przejściu ukła-
du od jednego stanu zwanego początkowym do drugiego zwanego końcowym poprzez conitnu-
um stanów pośrednich.
Przemiana jest odwracalna, jeśli od jej stanu końcowego do początkowego można po-
wróci w taki sposób, że i otoczeniu zostanie przywrócony stan pierwotny.
Odwzorowaniem przemiany w przestrzeni jest linia ciągła, łącząca kolejne punkty od
stanu początkowego do stanu końcowego. Równanie linii przemiany nazywamy równaniem
przemiany.
Pomiędzy dwoma stanami czynnika termodynamicznego można zrealizować nieskończe-
nie wiele przemian termodynamicznych. Spośród nich wyróżniamy przemiany charakterystycz-
ne: przemiana przy stałym ciśnieniu, przemiana przy stałej objętości, przemiana przy stałej tem-
peraturze, przemiana politropowa.
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
10
Gdy do układu nie dopływa ani nie odpływa substancja przemiany, którym poddawany
jest czynnik termodynamiczny nazywamy zamkniętymi. Jeśli podczas przemian układ pobiera
lub oddaje na zewnątrz substancje przemiany te nazywamy otwartymi.
2.2 Energia wewnętrzna układu
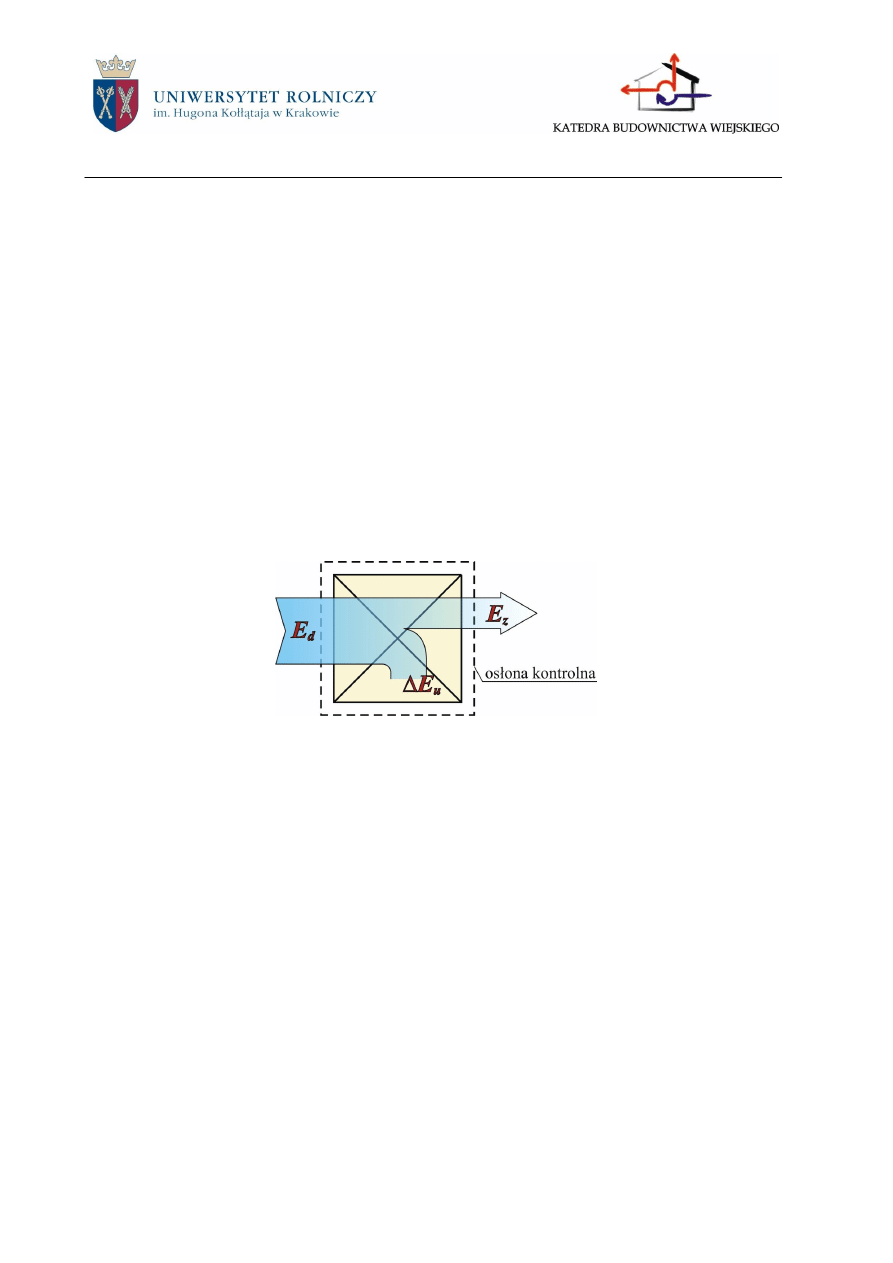
Jeśli do układu doprowadzimy energię (E
d
) część z niej pozostaje w układzie (E
u
) zmienia-
jąc jego energię wewnętrzną, część odprowadzana jest na zewnątrz układu (E
z
). Opierając się na
zasadzie zachowania energii można więc napisać równanie bilansu energii:
;
z
u
d
E
E
E
(2.1)
gdzie:
E
d
–
energia doprowadzona do układu;
E
u
–
przyrost energii układu;
E
z
–
energia odprowadzona z układu.
Rys.2.2. Wykres Sankey’a bilansu energii.
Bilans energii jest często przedstawiany w postaci wykresu Sankeya (rys.2.2).
W urządzeniach technicznych najczęściej spotyka się cztery sposoby przekazywania ener-
gii: za pomocą prądu elektrycznego, przez wykonanie pracy mechanicznej, przez przepływ cie-
pła, za pomocą strugi czynnika.
Energia każdego ciała jest sumą jego energii potencjalnej, kinetycznej, wewnętrznej.
Energia wewnętrzna (U) ciała fizycznego jest więc równa różnicy między jego energią całko-
witą a zewnętrzną energią mechaniczną. Energia wewnętrzna zawiera w sobie różne rodzaje
energii np. potencjalną, kinetyczną, chemiczną, sprężystą
.
Energia wewnętrzna ciał stałych, cie-
czy oraz gazów i par (doświadczenie Gay-Lussaca) zależy tylko od ich temperatury.
W zagadnieniach technicznych posługujemy się głównie przyrostami energii wewnętrznej.
W związku z tym przyjęcie parametrów, przy których energia wewnętrzna ma wartość zero, mo-
że być dowolne.
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
11
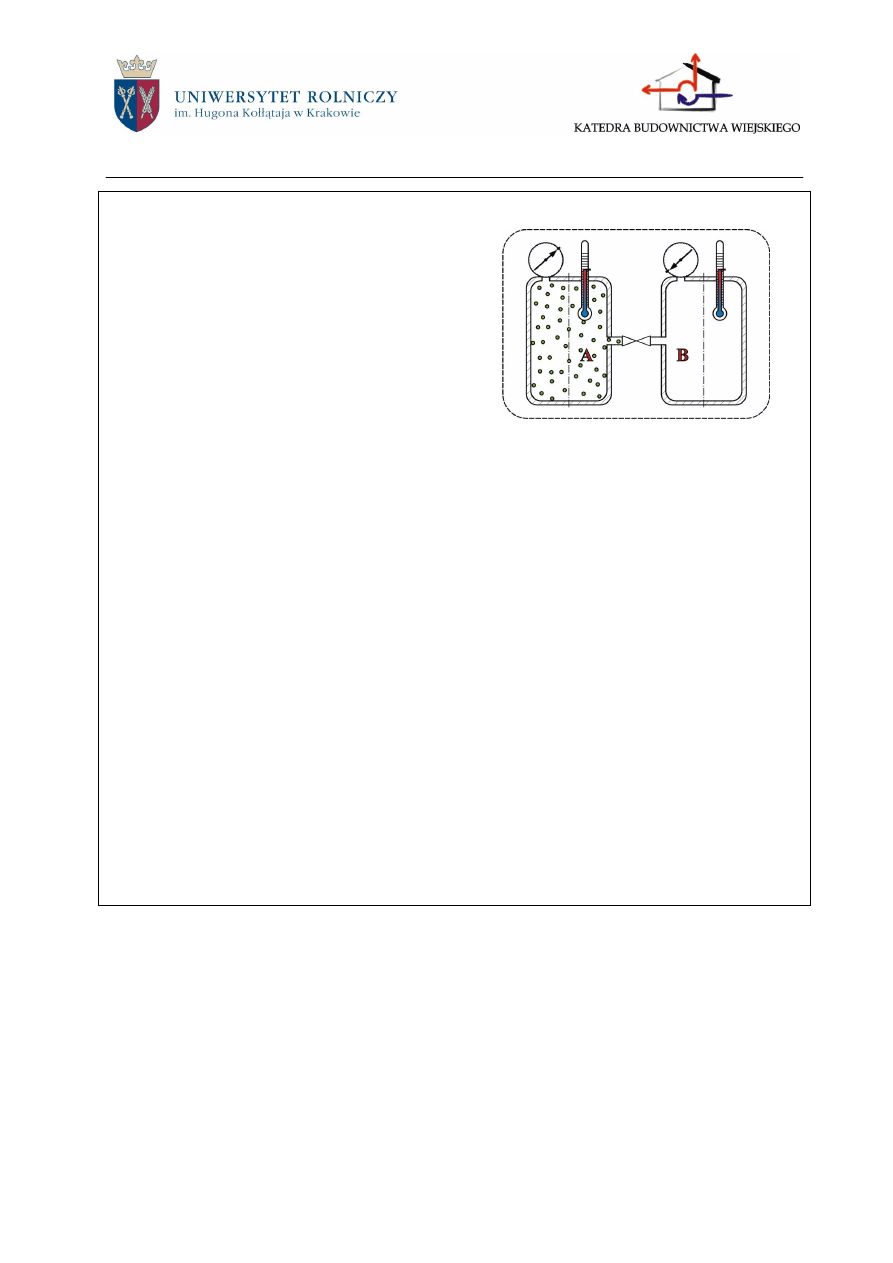
Doświadczenie Gay-Lussaca
Dwa zaizolowane zbiorniki połączono ze
sobą rurką, na której umieszczono zawór
(rys. 2.3). W zbiorniku A znajdował się gaz
o temperaturze t
1
pod ciśnieniem p
1
. W zbiorni-
ku B była natomiast zupełna próżnia. Po otwar-
ciu zaworu ciśnienia i temperatury w obu zbior-
nikach wyrównały się. Okazało się, że ciśnienie
p
2
panujące w obu zbiornikach jest mniejsze od
ciśnienia p
1
panującego przedtem w zbiorniku A.
Jeżeli obydwa zbiorniki otoczymy osłoną kontrolną i rozpatrzymy tak wyodrębniony
układ, to przekonamy się, że energia wewnętrzna gazu nie uległa zmianie, gdyż żadnej energii
do niego nie doprowadzono ani też od niego nie odprowadzono. Widzimy więc, że pomimo
zmiany ciśnienia i objętości nie zmieniła się energia wewnętrzna czynnika, chociaż zmieniła się
jego egzergia.
Gdy znajdujący się przed doświadczeniem w zbiorniku A czynnik miał takie parametry,
że można go było traktować jak gaz doskonały lub półdoskonały, to wspólna temperatura t
2
,
która ustaliła się w obu zbiornikach po otwarciu zaworu, jest równa temperaturze t
1
, która pa-
nowała w zbiorniku A przed otwarciem zaworu. Zatem do zmiany energii wewnętrznej gazu
zależna jest jedynie od zmiany temperatury gazu.
Jeżeli przyjmiemy, że energia wewnętrzna gazu doskonałego w temperaturze 0 K wynosi
zero, to energia wewnętrzna tego gazu o dowolnej temperaturze T K równa jest ilości ciepła,
które musimy doprowadzić, aby ogrzać ten gaz od 0 K do T K.
Rys.2.3. Doświadczenie Gay-Lussaca i Joule’a.
Zmianę energii wewnętrznej dla ciał stałych i cieczy obliczyć można na podstawie nastę-
pującej zależności:
J];
[
ΔT
Mc
n
ΔT
c
m
ΔU
(2.2)
gdzie:
c
–
ciepło właściwe substancji, [J·kg
-1
·K
-1
];
m
–
masa substancji, [kg];
(Mc) –
molowe ciepło właściwe substancji, [J·mol
-1
·K
-1
];
n
–
ilość moli substancji, [mol];
T
–
przyrost temperatury substancji, [K].
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
12
W przypadku gazów i par wzór do obliczania przyrostu energii wewnętrznej przyjmuje postać:
J];
[
ΔT
Mc
n
ΔT
c
m
ΔU
v
v
(2.3)
gdzie:
c
v
–
ciepło właściwe przy stałej objętości, [J·kg
-1
·K
-1
];
(Mc
v
) –
molowe ciepło właściwe przy stałej objętości, [J·mol
-1
·K
-1
].
Wynika to z faktu, że wnioski wyciągnięte z doświadczenia Gay-Lussaca prawdziwe są jedynie,
gdy doprowadzone lub odprowadzone ciepło jest zużywane tylko do zmiany energii wewnętrz-
nej czynnika (a nie np. do wykonania pracy). Zatem ogrzewanie/chłodzenie musi odbywać się
przy stałej objętości.
2.3 Praca i ciepło przemiany
2.3.1 Praca przemiany
Praca (L) w mechanice definiowana jest jako iloczyn skalarny siły i drogi, tj. jako iloczyn
drogi przez rzut siły na kierunek przesunięcia. W termodynamice konieczne jest uogólnienie
pojęcia pracy, gdyż oprócz pracy mechanicznej może
wystąpić praca wykonana przez prąd elektryczny,
pole magnetyczne itp. Mówiąc w termodynamice o
pracy układu mamy na myśli wyłącznie pracę makro-
skopowych sił zewnętrznych, którą układ pobiera z
zewnątrz lub oddaje na zewnątrz – wskutek oddzia-
ływania z otoczeniem.
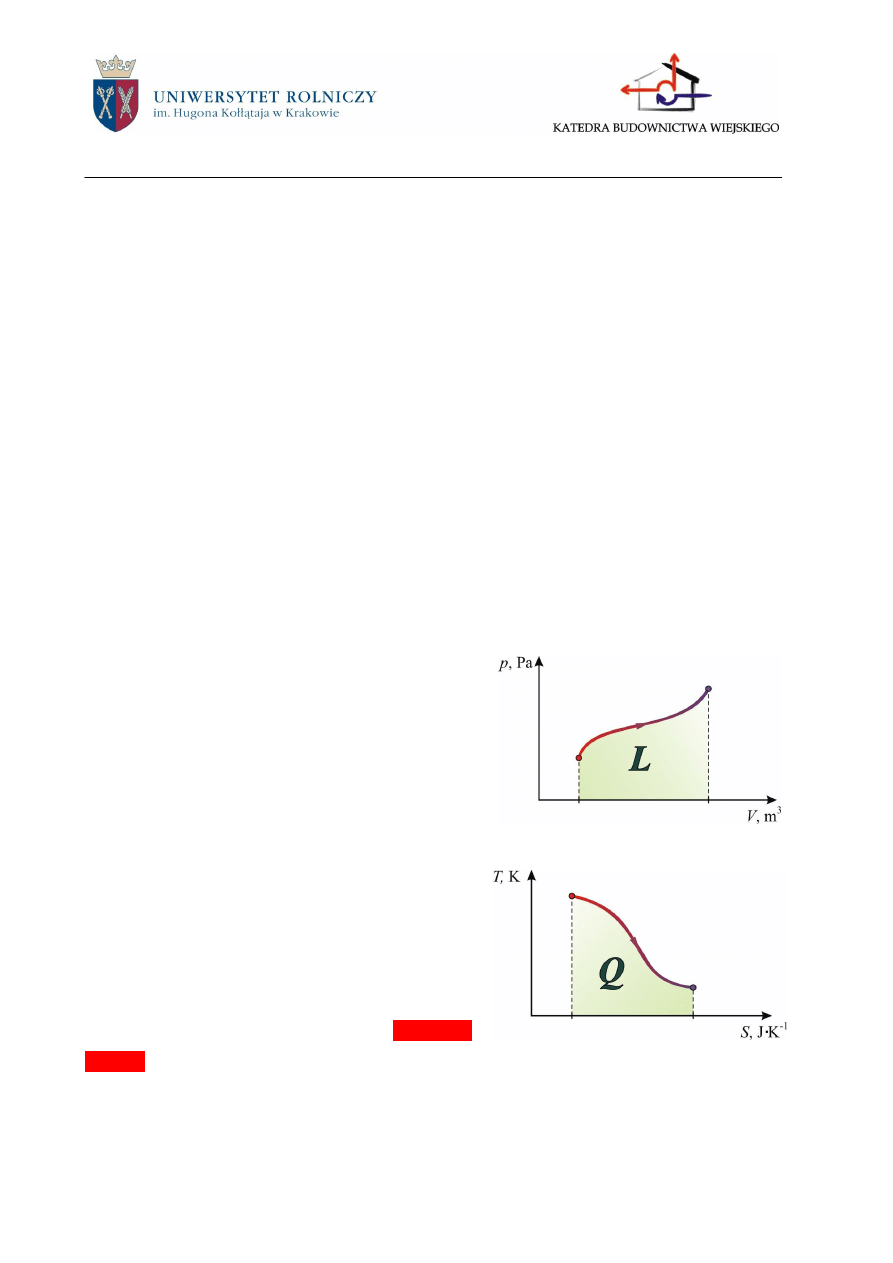
Praca przemiany graficznie przedstawiana jest
jako pole pod wykresem przemiany w układzie p-V
dlatego też układ ten nazywany jest układem pracy
lub układem Clapeyrona (rys.2.4).
Ciepło graficznie przedstawi można jako pole
pod wykresem przemiany w układzie T-S (entropia –
patrz…) dlatego też układ ten nazywany jest układem
pracy lub układem Belpaire’a (rys.2.5).
Rys.2.4. Układ pracy (Clapeyrona)
Rys.2.5. Układ ciepła (Belpiere’a)

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
13
Znak pracy jest umowny: pracę wykonywaną przez układ uważamy (w termodynamice tech-
nicznej) za dodatnią, natomiast praca wykonywana na układzie ma znak ujemny.
Praca zewnętrzna przemiany zależy od rodzaju przemiany, a w celu jej obliczenia należy
znać charakterystyczną dla tej przemiany zależność ciśnienia od objętości.
Typowym w termodynamice przykładem wykonania pracy jest oddziaływanie tłoka na
czynnik termodynamiczny zamknięty w cylindrze.
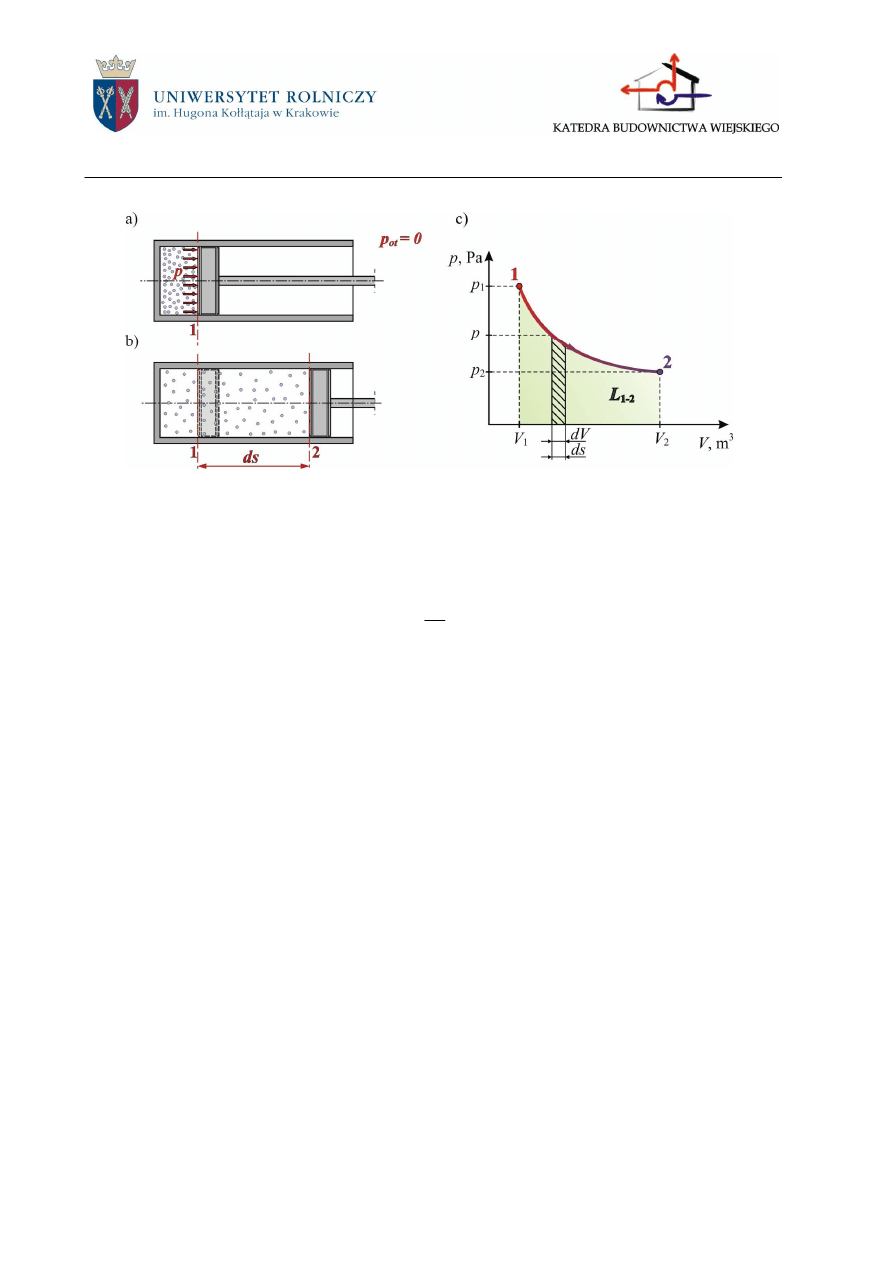
2.3.1.1 Praca bezwzględna
Praca bezwzględna (absolutna, zewnętrzna) (L) definiowana jest jako praca przekazywa-
na przez czynnik termodynamiczny na wewnętrzną stronę tłoka w zamkniętym cylindrze
(rys.2.6a), przy założeniu, że ciśnienie otoczenia jest równe zero (p
ot
= 0). Jest to praca związana
ze zmianą objętości czynnika (rys.2.6b). Znak pracy bezwzględnej zależny jest od znaku zmiany
objętości. Całkowita praca zmiany objętości przemiany miedzy stanami 1 i 2, równa w danym
przypadku całkowitej pracy przemiany, jest określona przez całkę:
[J];
)
(
2
1
2
1
V
V
dV
V
p
L
(2.4)
gdzie:
p
–
ciśnienie czynnika termodynamicznego, [Pa];
V
–
objętość czynnika termodynamicznego, [m
3
].
Praca ekspansji jest dodatnia, natomiast praca kompresji jest ujemna.
Zgodnie z interpretacją graficzną całki oznaczonej, pracę bezwzględną (pracę zmiany obję-
tości) można przedstawić na wykresie p-V za pomocą pola zawartego między liniami przemiany,
jej skrajnymi rzędnymi oraz osią odciętych (rys.2.6c).
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
14
Po przekształceniu równania 2.4, z uwzględnieniem równania stanu gazu doskonałego,
przyjmuje ono następującą postać:
[J];
2
1
2
1
V
V
T
R
m
L
(2.4a)
gdzie:
m
–
masa czynnika termodynamicznego, [kg];
R
–
indywidualna stała gazowa czynnika termodynamicznego, [J·kg
-1
·K
-1
];
T
–
temperatura czynnika termodynamicznego, [K];
V
1
–
objętość początkowa czynnika termodynamicznego, [m
3
];
V
2
–
objętość końcowa czynnika termodynamicznego, [m
3
].
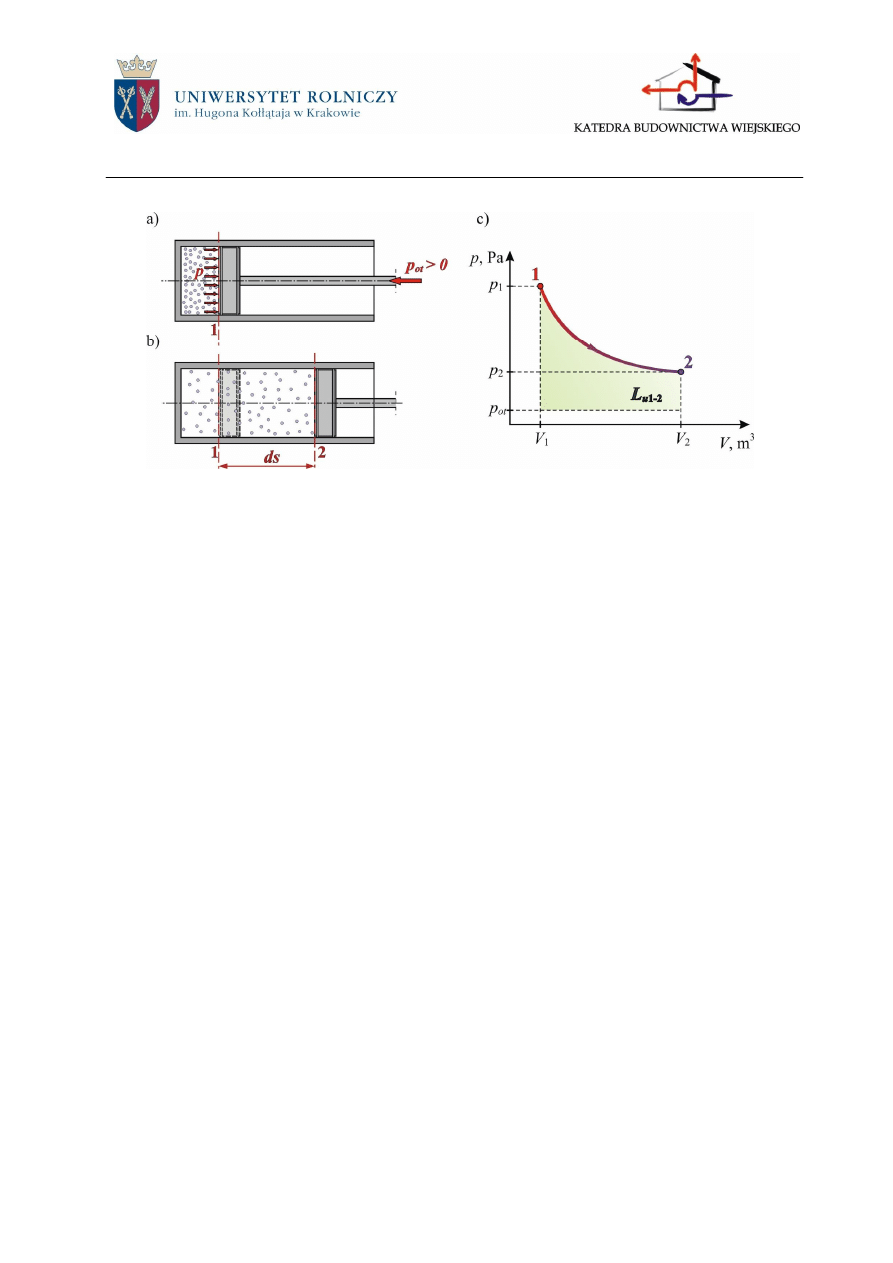
2.3.1.2 Praca użyteczna
Jeżeli ciśnienie na zewnątrz cylindra jest większe od zera (p
ot
> 0), to część pracy bez-
względnej zużywa się na pokonanie siły działającej na tłok pochodzącej od ciśnienia otoczenia
(rys.2.7a,b). Zatem praca użyteczna (Lu) jest to praca bezwzględna pomniejszona o pracę kom-
presji otoczenia:
[J];
)
(
1
2
1
2
2
1
2
1
2
1
V
V
p
dV
V
p
V
V
p
L
L
ot
V
V
ot
u
(2.5)
gdzie:
L
1-2
–
praca bezwzględna przemiany, [J];
p
–
ciśnienie czynnika termodynamicznego, [Pa];
p
ot
–
ciśnienie otoczenia, [Pa];
V
–
objętość czynnika termodynamicznego, [m
3
].
Rys.2.6. Praca bezwzględna przemiany: a) i b) zmiana objętości czynnika termodynamicznego cylin-
drze z tłokiem, c) graficzna interpretacja w układzie p-V
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
15
Graficznie pracę użyteczną, można przedstawić w układzie p-V za pomocą pola zawartego
między liniami przemiany, jej skrajnymi rzędnymi oraz osią odciętych pomniejszonego o pole
powierzchni prostokąta zawartego między skrajnymi rzędnymi przemiany, osią odciętych oraz
wartością ciśnienia otoczenia (rys.2.7c)
2.3.1.3 Praca techniczna
Pracą techniczną (L
t
) nazywamy sumę prac bezwzględnych wykonanych w jednym cyklu
maszyny przepływowej (maszyny, w których czynnik stale lub periodycznie do nich dopływa
i dopływa, takie jak: silniki tłokowe, turbiny parowe, sprężarki, pompy), w której realizowana
jest przemiana.
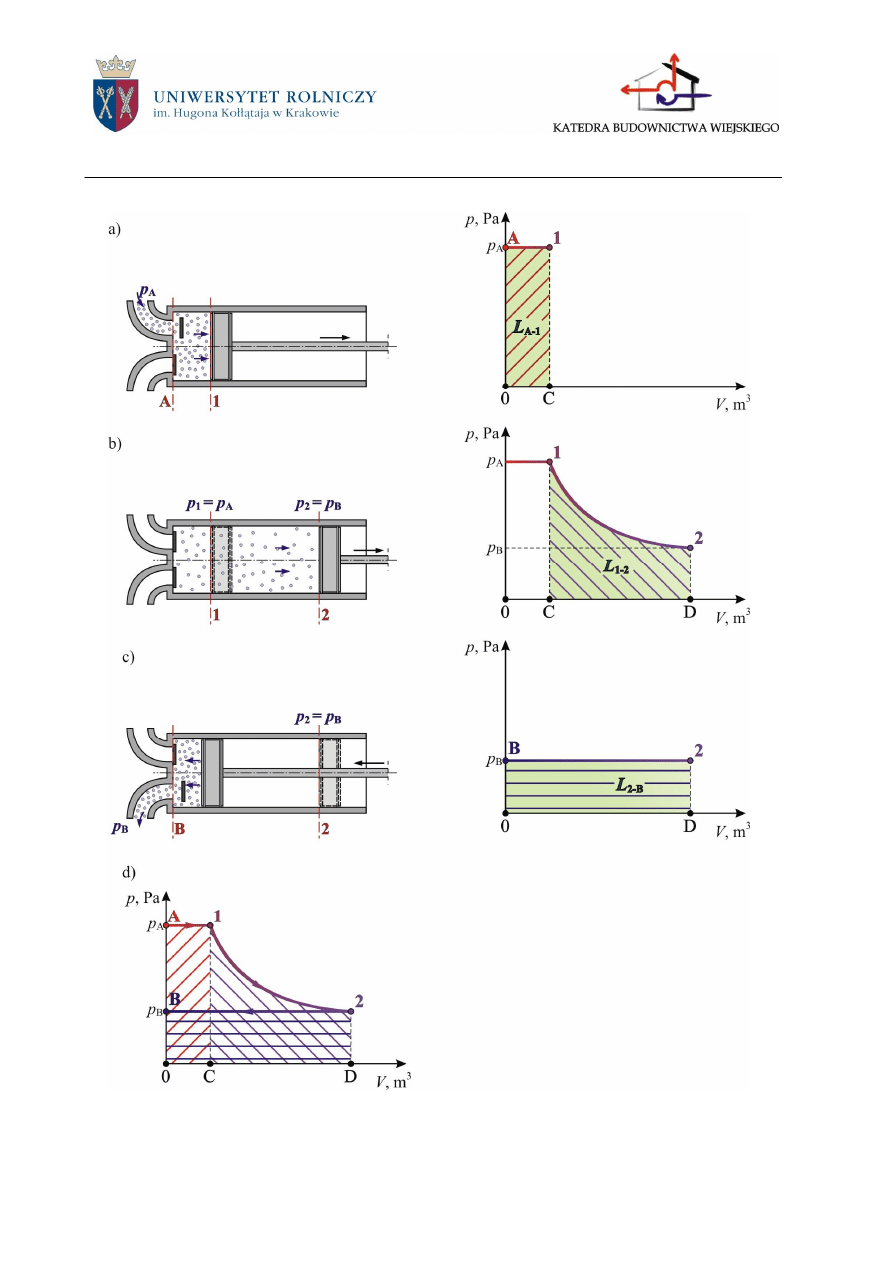
Jeden cykl pracy takiego silnika składa się z trzech kolejnych przemian odwracalnych.
1. Napełnianie cylindra (rys. 2.8a). Tłok przesuwa się z położenia początkowego A, w którym
był dosunięty do dna cylindra, do położenia 1. Przez otwarty zawór wlotowy dopływa wtedy
do cylindra czynnik z rurociągu, zatem jest to przemiana otwarta. Podczas tej przemiany ci-
śnienie w cylindrze nie zmienia się i jest ciągle równe ciśnieniu panującemu w rurociągu do-
lotowym.
Rys.2.7. Praca użyteczna przemiany: a) i b) zmiana objętości czynnika termodynamicznego cylindrze
z tłokiem, c) graficzna interpretacja w układzie p-V
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
16
Rys.2.8. Praca idealnego silnika przepływowego: a) napełnianie, b) ekspansja, c) wydmuch, d) praca
jednego cyklu
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
17
2. Rozprężanie się czynnika (rys. 2.8b). Obydwa zawory są zamknięte zatem jest to przemiana
zamknięta. Objętość czynnika rośnie, a ciśnienie jego maleje. Przemiana ta trwa aż do chwili,
w której ciśnienie czynnika staje się równe ciśnieniu panującemu w rurociągu wylotowym.
Ciśnienie to osiąga czynnik w chwili, w której tłok znajduje się w położeniu zwrotnym (2)
(tj. w położeniu, w którym kierunek jego ruchu zmienia się na przeciwny).
3. Wydmuch (rys. 2.8c). Tłok przesuwa się z położenia 2 do położenia końcowego B. Ponieważ
zawór wylotowy jest wtedy otwarty, więc przemiana ta jest otwarta. Ciśnienie w cylindrze
jest podczas tej przemiany stałe i równe ciśnieniu panującemu w rurociągu wylotowym.
Przemiana ta kończy się, gdy tłok dotknie dna cylindra.
Podczas przemian A-l i 1-2 objętość zajmowana przez czynnik powiększa się, więc prace
L
A-1
i L
1-2
mają wartości dodatnie. Natomiast podczas przemiany 2-B objętość zajmowana przez
czynnik maleje, więc praca L
2-B
ma wartość ujemną (w celu usunięcia czynnika z cylindra trzeba
pracę włożyć).
Sumę algebraiczną trzech prac bezwzględnych: pracy napełniania, pracy rozprężania i pra-
cy wydmuchu nazywamy pracą techniczną. W przypadku sprężarki będzie to suma algebraiczna
pracy ssania, pracy sprężania i pracy tłoczenia.
Z rysunku 2.8d wynika, że praca techniczna, którą wykonał czynnik w idealnej maszynie
przepływowej (podczas jednego cyklu pracy tej maszyny) przedstawiona jest polem F
A-1-2-B-A
.
Zatem graficznie pracę techniczną przemiany odwracalnej przedstawia na wykresie p-V pole
zawarte pomiędzy linią obrazującą daną przemianę a rzutem tej linii na oś rzędnych (rys.2.9).
Praca techniczna ma wartość dodatnią, gdy ciśnienie czynnika obniża się; natomiast wartość
Rys.2.9. Graficzna interpretacja pracy
technicznej w układzie p-V
Rys. 2.10. Zależność między pracą
bezwzględną a techniczną

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
18
ujemną, gdy ciśnienie czynnika wzrasta. Zatem wartość pracy technicznej przemiany obliczyć
można z następującego wzoru:
[J];
)
(
2
1
2
1
p
p
t
dp
p
V
L
(2.6)
gdzie:
p
–
ciśnienie czynnika termodynamicznego, [Pa];
V
–
objętość czynnika termodynamicznego, [m
3
].
Praca techniczna jest to iloczyn objętości elementarnego ubytku ciśnienia i nie zależy od rodzaju
maszyny przepływowej.
Jak wynika z rysunku przedstawiającego zależność między pracą bezwzględną a pracą
techniczną (rys.2.10) pomiędzy tymi dwoma wielkościami zachodzi następująca zależność
[J];
2
2
1
1
2
1
2
1
V
p
V
p
L
L
t
(2.7)
gdzie:
p
–
ciśnienie czynnika termodynamicznego, [Pa];
V
–
objętość czynnika termodynamicznego, [m
3
].
Uwaga!
Wzory 2.4 ÷ 2.7 są prawdziwe dla przemian, w których nie występuje tarcie wewnątrz
układu ani tarcie tłoka o gładź cylindra.
2.3.2 Ciepło przemiany
Jeżeli przez osłonę kontrolną jest przekazywana energią nie będąca pracą, czyli energia
której przepływ jest wymuszony różnicą temperatur, to ten sposób przekazywania energii nazy-
wamy ciepłem (Q). Ciepło pobrane w przemianie można obliczyć za pomocą wzoru:
[J];
1
2
2
1
2
1
2
1
T
T
c
m
dT
c(T)
m
Q
|
T
T
T
T
(2.8)
gdzie:
|
2
1
T
T
c
–
pojemność cieplna właściwa dla danego zakresu temperatur, [J·kg
-1
·K
-1
];
m
–
masa ciała, [kg];
T
1
, T
2
–
temperatura początkowa i końcowa ciała, [K].
Przyjmujemy umowę, że ciepło doprowadzone do układu będziemy uważać za dodatnie,
zaś ciepło wyprowadzone z układu za ujemne.

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
19
2.4 Entalpia entropia
2.4.1 Entalpia
Entalpia (I) (zawartość ciepła) jest to wielkość fizyczna będąca funkcją stanu mająca wy-
miar energii, będąca też potencjałem termodynamicznym, którą definiuje zależność:
[J];
V
p
U
I
(2.9)
gdzie:
U
–
energia wewnętrzna czynnika termodynamicznego, [J];
p
–
ciśnienie czynnika termodynamicznego, [Pa];
V
–
objętość czynnika termodynamicznego, [m
3
].
Entalpia jest równa sumie energii wewnętrznej (energii jaka jest potrzebna do utworzenia układu
gdy jest on tworzony w otoczeniu próżni) oraz iloczynu ciśnienia i objętości, który jest równy
pracy jaką należy wykonać nad otoczeniem by w danych warunkach uzyskać miejsce na układ.
Entalpia gazów doskonałych i półdoskonałych oraz powietrza wilgotnego zostanie omó-
wiona w rozdziale…
2.4.2 Entropia
Entropia (S) jest to termodynamiczna funkcja stanu, określająca kierunek przebiegu pro-
cesów samorzutnych w odosobnionym układzie termodynamicznym. Entropia jest miarą stopnia
nieuporządkowania układu albo inaczej mówiąc, stopień jego wyjątkowości. Entropia jest czyn-
nikiem całkującym dla temperatury aby otrzymać ciepło – nie da się jej zmierzyć:
[J];
dS
T
Q
d
(2.10)
gdzie:
Q
d
–
ciepło doprowadzone do czynnika z zewnętrznego źródła, [J];
T
–
temperatura bezwzględna rozpatrywanego czynnika termodynamicznego, [K].
zatem elementarny przyrost entropii ciała jest równy ilorazowi elementarnej ilości ciepła, którą
pochłonęło to ciało, przez temperaturę bezwzględną, jaką miało to ciało w momencie pochłania-
nia ciepła:
.
]
K
[J
1
T
dQ
dS
d
(2.11)
Na ogół w przemianach termodynamicznych nie interesuje nas entropia jako taka, ale jej
zmiany. Poziom zerowy jest przyjmowany umownie. Przy założeniu, że czynnik ma temperaturę
Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
20
0C i znajduje się pod ciśnieniem 0,1 MPa entropię właściwą można obliczyć z następujących
zależności:
dla ciał stałych i cieczy:
];
K
kg
[J
273
ln
1
1
T
c
s
(2.12)
gdzie:
c
–
ciepło właściwe ciała, [J·kg
-1
·K
-1
];
T
–
temperatura bezwzględna rozpatrywanego czynnika termodynamicznego, [K].
dla gazów doskonałych
];
K
kg
[J
10
ln
273
ln
1
1
p
R
T
c
s
p
(2.13)
gdzie:
c
p
–
ciepło właściwe przy stałym ciśnieniu, [J·kg
-1
·K
-1
];
p
–
ciśnienie bezwzględne, [MPa];
R
–
indywidualna stała gazowa, [J·kg
-1
·K
-1
].
2.5 Pierwsza zasada termodynamiki
Aby wyprowadzić równanie pierwszej zasady termodynamiki
1
przyjrzyjmy się bilansowi
energii przemiany termodynamicznej oraz maszyny przepływowej.
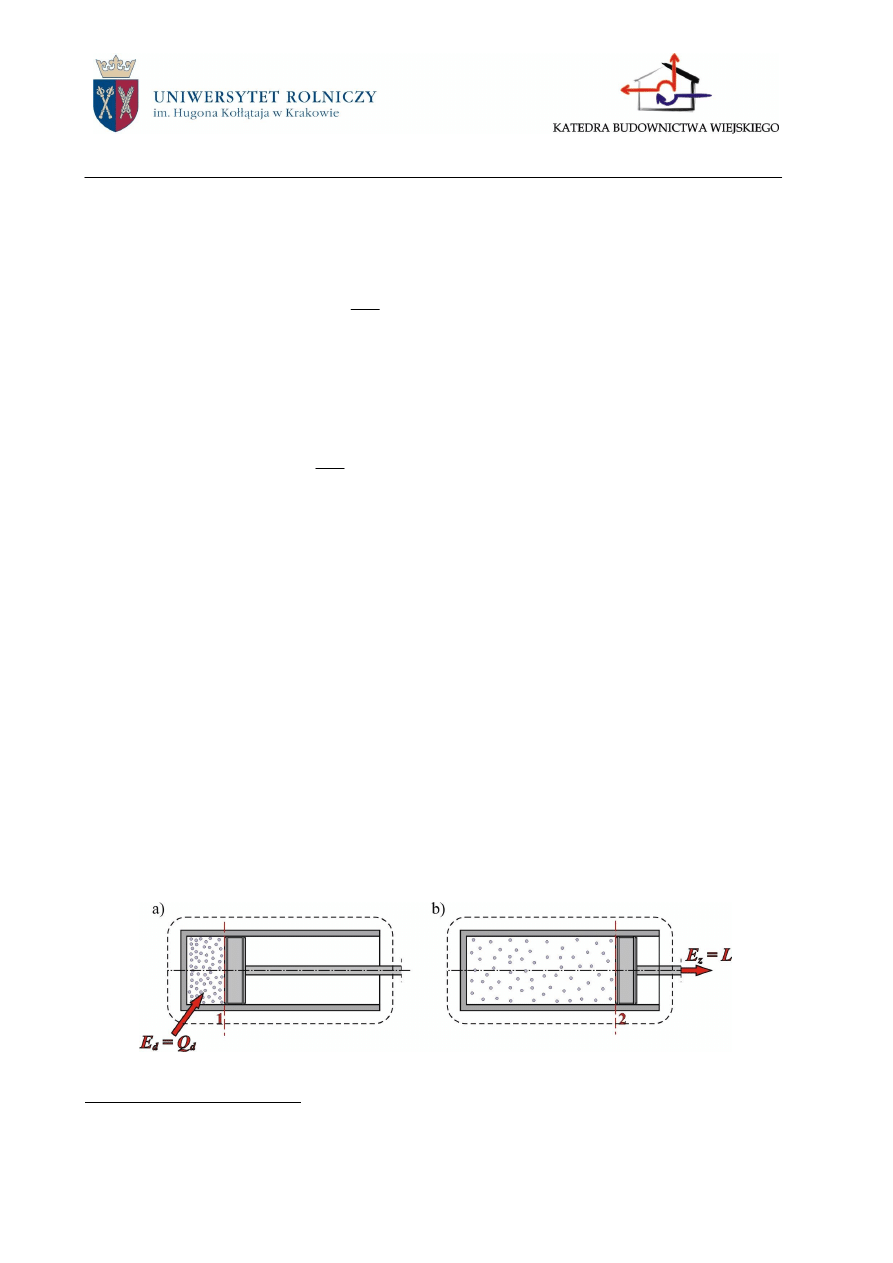
2.5.1 Bilans energii przemiany termodynamicznej
W poziomym cylindrze po jednej stronie tłoka, który porusza się bez tarcia, znajduje się
badany czynnik, a po drugiej jest próżnia. Przez osłonę kontrolną, którą otoczony jest tłok, do-
prowadzono pewną ilość ciepła E
d
= Q
d
, pod wpływem którego objętość czynnika zwiększyła
się, wskutek czego tłok przesunął się od położenia początkowego 1 (rys.2.11a) do położenia
końcowego 2 (rys.2.11b).
Rys.2.11. Bilans energetyczny przemiany zamkniętej
1
Zasada ta, równoważna zasadzie zachowania energii, w zarysach sformułowana została w 1842 przez J.R. Mayera,
uściślona zaś w 1847 przez H.L.F. de Helmholtza.

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
21
Przy założeniu, że metal z którego zrobione są cylinder i tłok, nie zmienia podczas prze-
miany swej temperatury, energia potencjalna i kinetyczna czynnika nie zmieniła się. Przyrost
energii układu jest zatem równy tylko przyrostowi energii wewnętrznej czynnika
E
u
=
U.
Energia odprowadzona była z układu za pomocą drąga tłokowego, który wyniósł ją poza osłonę
kontrolną. Energia ta została zużyta na pracę L wykonywaną przez czynnik przeciwko sile za
pomocą której tłok naciska z zewnątrz na gaz. Z tego powodu praca ta, jak też każda praca, którą
wykonuje czynnik przeciw sile działającej na niego z zewnątrz, nazywana bywa pracą ze-
wnętrzną. W rozpatrywanym przykładzie praca ta jest równa energii odprowadzonej z układu:
E
z
= L. Podstawiając tak zdefiniowane wartości do równania bilansu energii (2.1) otrzymamy
następujące równanie:
[J];
L
U
Q
d
(2.14)
gdzie:
L
–
praca przemiany, [J];
U
–
xmiana energii wewnętrznej czynnika, [J].
Wzór ten nosi nazwę pierwszej postaci równania pierwszej zasady termodynamiki dla prze-
miany termodynamicznej, która głosi, że:
Ciepło doprowadzone do układu jest zużywane na wykonanie pracy bezwzględnej i przy-
rost energii wewnętrznej tego układu.
Gdy stan czynnika na początku przemiany nazwiemy stanem 1, a na końcu stanem 2, to
wzór 2.14 przyjmie następującą postać:
[J].
1
2
2
1
L
U
U
Q
(2.14a)
2.5.2 Bilans energii przemiany termodynamicznej
Bilans ten przeprowadzimy dla jednego pełnego cyklu pracy silnika. Energia dopływająca
w tym czasie do cylindra jest sumą entalpii doprowadzonego przez zawór wlotowy czynnika
i ciepła doprowadzanego przez ścianki cylindra: E
d
= I
d
+ Q
d
. Ponieważ po każdym pełnym cy-
klu układ wraca do tego samego stanu, więc przyrost energii układu jest równy zeru:
E
u
= 0.
Energia odprowadzana z układu jest sumą pracy technicznej przemiany 1-2 i entalpii czynnika
odprowadzanego przez zawór wylotowy: E
z
= L
t
+ I
z
. Po wstawieniu tych wartości do równania
bilansu energii (2.1) otrzymuje się wyrażenie

Materiały pomocnicze do przedmiotu Termodynamika techniczna. Rozdział 2
mgr inż. Agnieszka Sadłowska-Sałęga
22
;
z
t
d
d
I
L
Q
I
(2.15)
gdzie:
I
d
–
entalpia początkowa czynnika, [J];
I
z
–
entalpia początkowa czynnika, [J];
L
t
–
praca techniczna wykonana przez czynnik, [J];
Q
d
–
ciepło dostarczone do układu, [J];
a po przekształceniu:
[J];
t
d
L
I
Q
(2.15a)
gdzie:
I
–
przyrost entalpii czynnika, [J].
Wzór (2.15a) nosi nazwę drugiej postaci równania pierwszej zasady termodynamiki. Zatem
pierwszą zasadę termodynamiki można również sformułować następująco:
Ilość ciepła doprowadzonego do czynnika podczas przemiany termodynamicznej równa się
sumie przyrostu entalpii czynnika i pracy technicznej, którą czynnik wykonał.
Uwaga!
Znane są również inne sformułowania pierwszej zasady termodynamiki:
1. Energia wewnętrzna układu zamkniętego nie zmienia się, niezależnie od przemian zacho-
dzących w tym układzie.
2. Niemożliwe jest skonstruowanie perpetuum mobile pierwszego rodzaju, czyli silnika pracu-
jącego bez zasilania energią z zewnątrz.
3. Zmiana energii wewnętrznej układu jest równa sumie pracy wykonanej przez układ bądź
nad układem i ciepła dostarczonego lub oddanego przez układ.
Wyszukiwarka
Podobne podstrony:
2 2 pierwsza zasada termodynamiki
Pierwsza zasada termodynamiki
Pierwsza zasada termodynamiki
Pierwsza zasada termodynamiki
3 PIERWSZA ZASADA TERMODYNAMIKI
Pierwsza i druga zasada termodynamiki (entropia, zjawiska odwracalne)
zasada termodynamiki, 1 zasada termodynamiki - zmiana energii wewnętrznej układu równa jest sumie ci
Pierwsza i druga zasada termodynamiki (entropia, zjawiska odwracalne)
Pierwsza i druga zasada termodynamiki (entropia, zjawiska odwracalne)
I zasada Termodynamiki
Praca absolutna, ciepło właściwe, I zasada termodynamiki
18 entropia i II zasada termodynamiki
16 I zasada termodynamiki
Radiacyjny strumień ciepła i bilans energii dla powierzchni
I Zasada Termodynamiki rozszerzenie id 208487
zasada termodynamiki Nernsta (twierdzenie Nernsta)
Bilans energii elektrycznej pseudo konspekt
więcej podobnych podstron