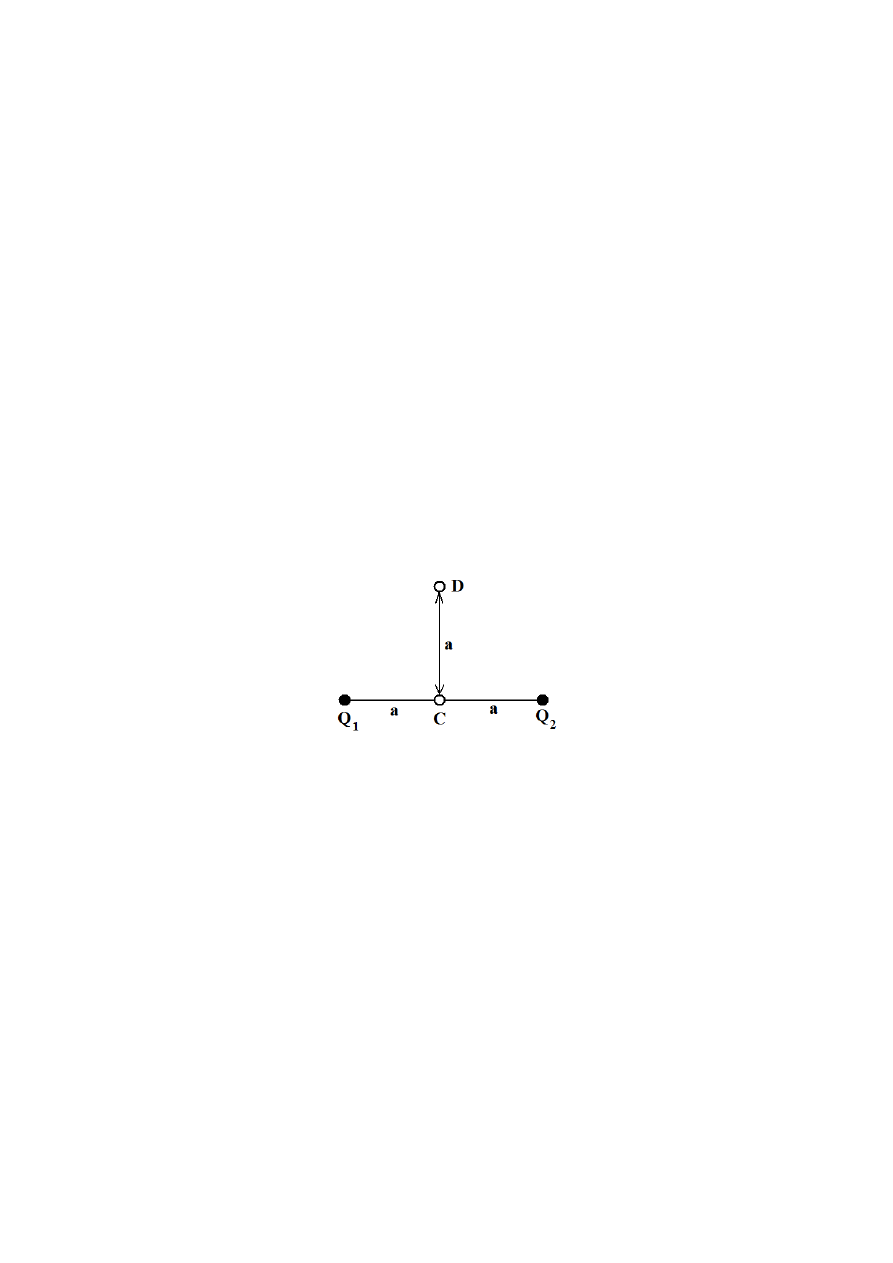
10. ELEKTROSTATYKA: Praca w polu elektrostatycznym
10.1. Oblicz jaką pracę należy wykonać by kulkę naładowaną ładunkiem Q przesunąć w jednorodnym
polu elektrostatycznym o natężeniu E na odległość x:
a.
wzdłuż linii sił pola,
b.
prostopadle do linii sił pola,
c.
wzdłuż prostej tworzącej z liniami sił pola kąt
α
.
10.2.Trzy ładunki punktowe q
a
= 3 10
-6
C, q
b
= 5 10
-6
C, q
c
= -6 10
-6
C znajdują się w wierzchołkach
trójkąta ABC (AB = 0,3 m, BC = 0,5 m, AC = 0,6 m). Obliczyć pracę, jaką należy wykonać aby
rozsunąć te ładunki na odległość, dla której można by założyć, że siły wzajemnego oddziaływania
ładunków równe są zeru. Ładunki znajdują się w nafcie.
10.3.W modelu Bohra atomu wodoru elektron krąży po orbicie kołowej o promieniu R, a proton
znajduje się w środku tej orbity. Ile wynosi prędkość elektronu? Ile wynosi elektryczna energia
potencjalna wyrażona w elektronowoltach? Ile wynosi całkowita energia mechaniczna wyrażona w
elektronowoltach?
10.4. Przyjmij, że w jądrze helu dwa protony są odległe od siebie o r = 1,5 10
-15
m. Jaka siła
elektrostatyczna działa między nimi? Ile pracy należy wykonać, by umieścić protony tuż koło siebie?
10.5. Elektron znajduje się w odległości r = 5,3 10
-11
m od protonu. Jakiej prędkości musi nabrać, by
uciec do nieskończoności?
10.6*. (N) Jaką pracę należy wykonać, aby naładować metalową kulę o promieniu R ładunkiem Q?
10.7. (N) Znaleźć pracę wykonaną przez siły pola, wytworzonego przez dwa punktowe ładunki, przy
przeniesieniu ładunku q =3 C z punktu C do punktu D, jeżeli a = 6 cm, Q
1
= 10 C, Q
2
= -6 C (rys).
10.8. (N) Jaką pracę należy wykonać, aby naładować do napięcia U płaski kondensator powietrzny o
polu powierzchni okładek S i odległości między nimi równej d? O ile zmieni się wartość tej pracy,
jeśli kondensator wypełnimy dielektrykiem o przenikalności
ε
?
Zagadka
10.9. (N) Metalowa kula została naładowana ładunkiem dodatnim (trwałe ładowanie przez indukcję).
Czy masa tej kuli się zmniejszy, zwiększy czy pozostanie bez zmian? Uzasadnij.

11. ELEKTROSTATYKA: Prawo Gaussa
11.1. Obliczyć potencjał i natężenie pola elektrycznego wewnątrz i na zewnątrz naładowanej
ładunkiem Q:
a) sfery o promieniu R
b) kuli o promieniu R wykonanej z przewodnika
c) nieprzewodzącej kuli o promieniu R
11.2. Wyznacz natężenie pola elektrostatycznego w punkcie oddalonym o x od środka wykonanej z
dielektryka wydrążonej kuli o promieniu R
z
(promień wydrążenia wynosi R
w
), na której zgromadzono
ładunek Q. Rozważ przypadki:
a.
x < R
w
b.
R
w
< x < R
z
c.
x > R
z
11.3. Wyznacz natężenie pola elektrostatycznego w punkcie oddalonym o x od osi nieskończenie
długiego, nieprzewodzącego, naładowanego pręta o promieniu R i gęstości liniowej ładunku
λ
.
Rozważ przypadki:
a.
x < R
b.
x > R
11.4. Wyznacz natężenie pola elektrostatycznego w odległości r od środka nieskończenie długiego,
wydrążonego, nieprzewodzącego, naładowanego pręta o promieniu R
z
i gęstości liniowej ładunku
λ
.
Promień wydrążenia wynosi R
w
. Rozpatrz trzy przypadki:
a.
r < R
w
b.
R
w
< r < R
z
c.
r > R
z
11.5. Kabel koncentryczny współosiowy składa się z drutu otoczonego wydrążonym przewodnikiem
walcowym. Załóżmy, że liniowe gęstości ładunku na tych przewodnikach są odpowiednio równe -
λ
i
λ
. Wyznacz natężenie pola elektrostatycznego pomiędzy przewodnikami i na zewnątrz przewodnika
walcowego.
11.6. Jakie jest pole elektryczne wytworzone przez nieskończenie dużą, nieprzewodzącą płaszczyznę
naładowaną jednorodnie? Gęstość powierzchniowa ładunku wynosi
σ
.
11.7. (N) Małą nieprzewodzącą kulkę o masie m = 1 mg i ładunku q = 2*10
-8
C (rozłożonym
jednorodnie w całej objętości kulki), zawieszona na izolowanej nici, tworzącej kąt
θ
= 30
o
z pionową,
jednorodnie naładowaną płytą. Uwzględniając siłę ciężkości i zakładając, że płyta rozciąga się daleko
w kierunku poziomym i pionowym, oblicz gęstość powierzchniową ładunku
σ
na płycie.
11.8. (N). Trzy płasko równoległe cienkie płytki umieszczone w małej odległości jedna od drugiej,
równomiernie naładowano. Gęstości powierzchniowe ładunków płytek są odpowiednio równe:
σ
1
= 3*10
-8
C/m
2
,
σ
2
= -5*10
-8
C/m
2
,
σ
3
= 8*10
-8
C/m
2
. Znaleźć natężenie pola w punktach leżących
pomiędzy płytkami i na zewnątrz płytek. Sporządź wykres E(r) przyjmując za początek układu
odniesienia pierwszą płytkę.
11.9.* (N). Przestrzeń wypełniona jest ładunkiem o gęstości
ρ
zmieniającej się według wzoru
ߩ =
ఘ
బ
, gdzie
ρ
0
jest wielkością stałą, a r – odległością od początku układu współrzędnych. Określić
wektor natężenia pola elektrycznego jako funkcję wektora położenia r.
Wyszukiwarka
Podobne podstrony:
ćwiczenia" 10 11
mat fiz 2003 10 11 id 282349 Nieznany
geometria wykreslna cwiczenia 10-11 3
fiz cwiczenia 10 odp
mat fiz 2004 10 11 id 282351 Nieznany
fiz cwiczenia 10
Patomorfologia cwiczenia(,10,11
nicienie cwiczenia 8 9 10 11 (2)
geometria wykreslna cwiczenia 10 11
fiz cwiczenia 10 odp
Antropologia widowisk, ćwiczenia I, 4 10 11
10.11.2010, prawo administracyjne ćwiczenia(2)
więcej podobnych podstron