Document Outline

1 / 1

Jagiellonian University

Theoretical

Computer Science

Co dzisiaj

Dzisiejszy wykład

Edward Szczypka

2 / 1

Jagiellonian University

Theoretical

Computer Science

spis

Edward Szczypka

3 / 1

Jagiellonian University

Theoretical

Computer Science

Poj ˛ecie Algorytmu

Algorytm

to sformalizowany sposób post ˛epowania przy rozwi ˛

azywaniu jakiego´s problemu.

Klasyczny przykład – przepisy kulinarne, instrukcje obsługi rozmaitych urz ˛

adze ´n

Algorytm:

pobiera dane wej´sciowe
wykonuje pewne (z góry przewidziane) operacje
daje dane wyj´sciowe

Pojecie danych mo˙zna rozumie´c bardzo szeroko

Algorytm powinien działa´c

poprawnie – tzn. zwraca´c zawsze poprawna odpowiedz
sko ´nczenie długo – nie powinien si ˛e p ˛etli´c

odpowiedz powinien zwraca´c w mo˙zliwie krótkim
anga˙zuj ˛

ac mo˙zliwie mało zasobów – np. pami ˛eci

Edward Szczypka

4 / 1

Jagiellonian University

Theoretical

Computer Science

Algorytm vs Program

Program

to algorytm zapisany w jakims jezyku (programowania).

program ma zwykle postac ciagu polecen, które nalezy wykonywac po kolei (chyba, ze w
samym programie przewidziana jest zmiana kolejnosci)

ten sam algorytm mozna zapisac w róznych jezykach, zwykle na wiele sposobów

Przykład 1 Algorytm ustawiania zadanej stacji w radiu:

1) Dowiedz sie, na jakiej czestotliwosci nadaje Twoja ulubiona stacja. (To sa dane wejsciowe.)

2) Nacisnij piaty guzik w siódmym rzedzie.

3) Wpisz czestotliwosc na klawiaturze.

4) Nacisnij zielony guzik pod fioletowa gałka.

5) Teraz powinno grac. (To jest rezultat - dane wyjsciowe.)

Edward Szczypka

5 / 1

Jagiellonian University

Theoretical

Computer Science

Algorytm vs Program

Rozwiazywanie równania kwadratowego:

Oznacz współczynniki równania symbolami a, b, c. (Dane wejsciowe.)

Policz ∆ = b

− 4ac.

Je´sli ∆ < 0, to koniec – nie ma pierwiastków rzeczywistych.

Je´sli ∆ = 0, to policz x

= −

b/2a.

Je´sli ∆ > 0, to policz x

−b+

√

∆

i x

−b−

√

∆

Program realizuj ˛

acy ten algorytm zapisany w pseudo-Pascalu:

read(a, b, c)

delta:=b*b-4*a*c
if delta<0 then

write(’Nie ma pierwiastków rzeczywistych’)

halt

if delta=0 then

x1:=-b/(2*a)
x2:=-b/(2*a)

if delta > 0 then

x1:=(-b+sqrt(delta))/(2*a)
x2:=(-b-sqrt(delta))/(2*a)

write(x1, x2)

Edward Szczypka

6 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle

Prawie kazdy wiekszy algorytm musi powtarzac pewne obliczenia, az do uzyskania jakiegos
rezultatu.

Taka sytuacja nazywana jest petla.

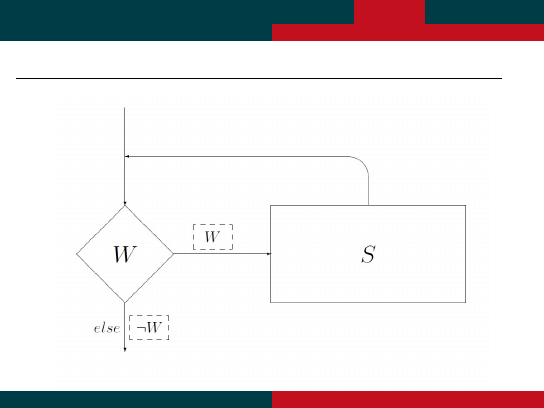
Typowa (i jedyna potrzebna tutaj) petla to:

WHILE

warunek DO polecenie

Taka petla:

sprawdza podany warunek
i jesli jest spełniony, to wykonuje podane polecenie
nastepnie ponownie sprawdza warunek
(wartosci dla których warunek jest sprawdzany mogły ulec zmianie przez wykonanie
polecenia)
i jesli jest spełniony, to wykonuje podane polecenie
nastepnie ponownie sprawdza warunek
i jesli jest spełniony, to wykonuje podane polecenie
. . .
. . .

Wyjscie z petli nastepuje wiec wtedy, gdy warunek nie jest spełniony

bo albo w ogóle nie był spełniony,
albo przestał byc spełniony na skutek wykonywania polecenia

Edward Szczypka

7 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle - graficznie

Edward Szczypka

8 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle – przykłady

Przykład 2 Wypisanie liczb od 1 do 100:

write(’Zaczynamy’)

x := 1

while x <= 100 do

write(x)

x := x + 1

write(’I to by było na tyle’)

W tym programie nie ma danych wej´sciowych.

Dane wyj´sciowe to wypisane liczby 1, 2, . . . , 100 (oraz ew. komentarze tekstowe).

Bardzo typowe jest podstawienie x := x + 1. Jego sens jest taki: zwi ˛eksz x o jeden.

Przykład 3 A co robi program?

read(a)

write(’Zaczynamy’)

x := 1

while x <= a do

x := x + 1

write(x)

write(’I to by było na tyle’)

Edward Szczypka

9 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle - problemy

P˛etle s ˛

a bardzo silnym narz ˛edziem programistycznym, ale mog ˛

a by´c powodem wielu komplikacji.

Istotne pytania to:

Czy algorytm/procedura zako ´nczy si ˛e?

Czy po zako ´nczeniu daje poprawne wyniki?

Jak długo trwa wykonanie procedury?

Ile pami ˛eci zu˙zywa procedura?

Do analizowania dwu pierwszych problemów słu˙z ˛

a tzw.

NIEZMIENNIKI P ˛

ETLI

Edward Szczypka

10 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle - Niezmienniki

W p ˛etli WHILE W DO S

jest warunkiem – formuła logiczna, od spełnienia której zale˙zy wykonywanie p ˛etli

jest lista czynno´sci wykonywanych w p ˛etli

NIEZMIENNIKIEM

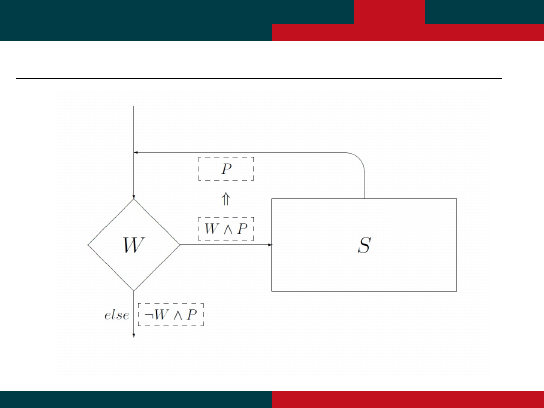
p ˛etli WHILE W DO S jest

warunek (formuła logiczna) P taki, ze:

je´sli W ∧ P zachodzi przed wykonaniem czynno´sci S
to P zachodzi po wykonaniu czynno´sci S.

U ˙

ZYTECZNA OBSERWACJA:

Je´sli:

P jest niezmiennikiem p ˛etli WHILE W DO S

P jest spełniony przy wej´sciu w te p ˛etle

to:

w ka˙zdym takcie p ˛etli warunek P jest spełniony

przy wyj´sciu z p ˛etli warunek P jest spełniony, a W juz nie.

Edward Szczypka

11 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle – Niezmienniki – Graficznie

Edward Szczypka

12 / 1

Jagiellonian University

Theoretical

Computer Science

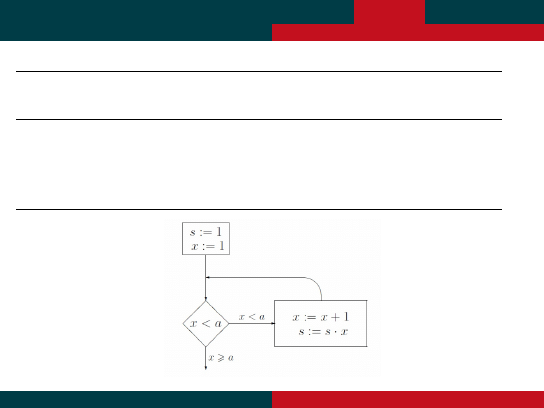
P˛etle – Liczenie Silni

INPUT: a<= 0

OUTPUT: s = a!

INITIAL:

s:=1

x:=1

WHILE x<a DO x:=x+1

s:=s*x

END

Edward Szczypka

13 / 1

Jagiellonian University

Theoretical

Computer Science

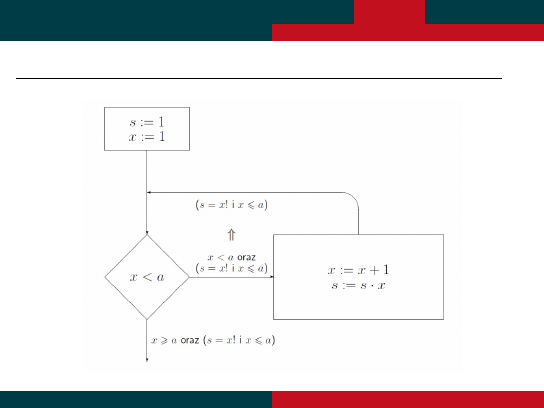
P˛etle - Liczenie Silni

Edward Szczypka

14 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle – Liczenie Silni – Analiza

Potrzebujemy wykaza´c, ˙ze po wyj´sciu z p ˛etli rzeczywi´scie s = a!. Najpierw pokazujemy, ze
niezmiennikiem petli jest warunek (s = x ! i x ¬ a): Skoro jest on spełniony przed wej´sciem w
p ˛etle, to mamy:

stare

i x

stare

¬ a

Czynno´sci p ˛etli zmieniaj ˛

a warto´sci x i s na:

nowe

stare

nowe

stare

nowe

stare

(

stare

sk ˛

ad s

nowe

stare

(

stare

1) = x

stare

1) = (x

stare

1)! = x

nowe

Nadto, skoro x

stare

nowe

stare

1 ¬ a.

Z kolei przy wyj´sciu z p ˛etli mamy:

x > a

s = x ! i x ¬ a

co daje x = a oraz s = x ! = a!.

Edward Szczypka

15 / 1

Jagiellonian University

Theoretical

Computer Science

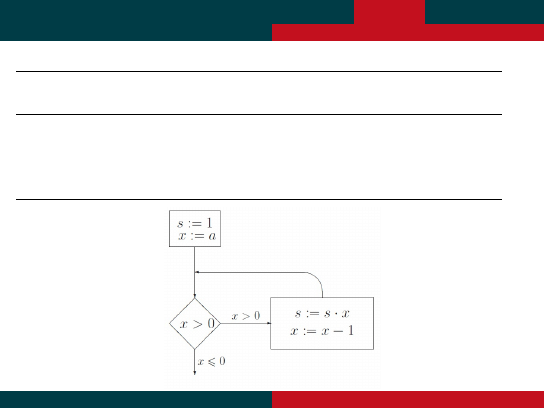
P˛etle – Liczenie Silni – inne liczenie Silni

INPUT: a <= 0

OUTPUT: s = a!

INITIAL:

s:=1

x:=a

WHILE x>0 DO s:=s*x

x:=x-1

END

Edward Szczypka

16 / 1

Jagiellonian University

Theoretical

Computer Science

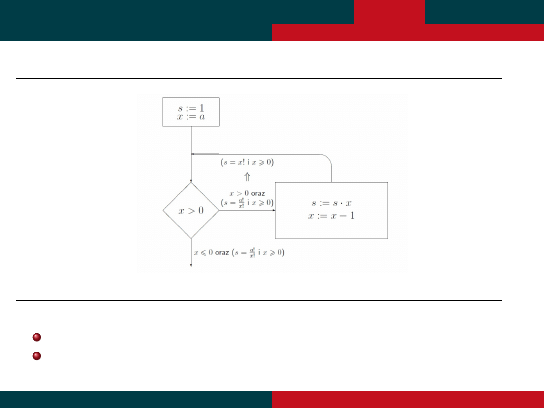
P˛etle – Liczenie Silni – inne liczenie Silni

Uzasadnij, ze:

wyra˙zenie podane w nawiasie jest rzeczywi´scie niezmiennikiem p ˛etli,

oraz gwarantuje poprawno´s´c wyniku tzn., ze przy wyj´sciu z p ˛etli s = a!.

Edward Szczypka

17 / 1

Jagiellonian University

Theoretical

Computer Science

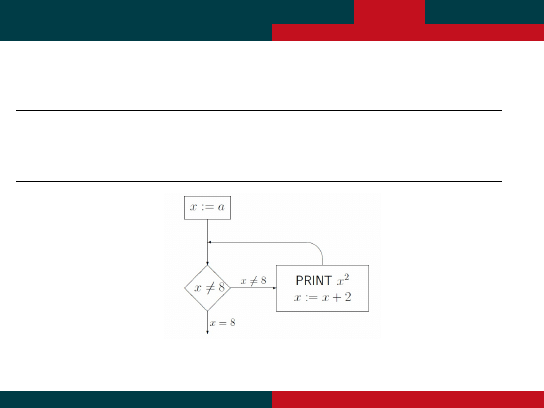
P˛etle i niezmienniki – Problem Stopu

INPUT: a <= 0

OUTPUT: ?

INITIAL: x:=a

WHILE x<>8 DO PRINT x^2

x:=x+2

END

Co robi powy˙zsza procedura i kiedy si ˛e zatrzymuje (dla jakich warto´sci a)?

Zauwa˙z, ze kolejno´s´c instrukcji w prostok ˛

acie jest istotna!

Edward Szczypka

18 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle i niezmienniki – Nierozwi ˛

azany Problem Stopu

INPUT: a >= 0

OUTPUT: ?

INITIAL: x:=a

WHILE x<>1 DO

IF x jest parzyste THEN

x:=x/2

ELSE

x:=3*x+1

END

Narysuj schemat blokowy tej procedury. Spróbuj znale´z´c niezmienniki p ˛etli. Spróbuj uzasadni´c,

˙ze zawsze si ˛e zatrzyma – na jakie kłopoty natrafiasz?

Ta procedura wygl ˛

ada na do´s´c prosta,

ale . . .

do dzi´s nie wiadomo, czy zawsze si ˛e zatrzymuje . . .

Edward Szczypka

19 / 1

Jagiellonian University

Theoretical

Computer Science

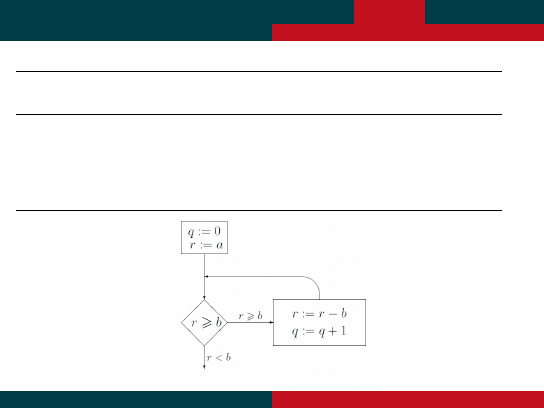
P˛etle i niezmienniki – dzielenie z reszt ˛

INPUT: liczby naturalne a >= 0, b > 0

OUTPUT: liczby naturalne q i r takie, ze a = qb + r oraz 0 <= r < b

INITIAL:

q:=0

r:=a

WHILE r>=b DO

r:=r-b

q:=q+1

END

Edward Szczypka

20 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle i niezmienniki – dzielenie z reszt ˛

a – analiza

Poka˙zemy, ze niezmiennikiem jest warunek:

0 ¬ r

i a = qb + r

Wtedy, przy wyj´sciu z p ˛etli mamy:

r < b

0 ¬ r i a = qb + r

czyli dokładnie nało˙zone przez nas warunki: a = qb + r oraz 0 ¬ r < b.
Spełnienie niezmiennika przy wej´sciu w p ˛etle oznacza, ˙ze:

0 ¬ r

stare

oraz a = q

stare

· b + r

stare

Z kolei przebieg p ˛etli zmienia warto´sci r i q na:

nowe

stare

− b

nowe

stare

sk ˛

ad mamy:

nowe

· b + r

nowe

= (

stare

1) · b + r

stare

− b = q

stare

· b + b + r

stare

− b = q

stare

· b + r

stare

Nadto, skoro czynno´sci p ˛etli wykonuj ˛

a si ˛e, to r

stare

b sk ˛

ad r

nowe

stare

− b > b − b = 0.

Edward Szczypka

21 / 1

Jagiellonian University

Theoretical

Computer Science

P˛etle i niezmienniki – szybkie pot ˛egowanie

INPUT: liczby naturalne a,n >= 0

OUTPUT: liczby naturalna b=a^n

INITIAL:

b:=1

x:=a

i:=n

WHILE i>0 DO

IF i jest nieparzyste THEN

b:=b*x
i:=(i-1)/2

ELSE

i:=i/2

x:=x*x

END

Narysuj schemat blokowy tego algorytmu.
Wykaz, ze niezmiennikiem p ˛etli jest x

· b = a

U˙zyj tego faktu do pokazania, ze ta procedura działa poprawnie.

Jaki inny warunek nale˙zy w tym celu umie´sci´c w niezmienniku?

Edward Szczypka

22 / 1

Jagiellonian University

Theoretical

Computer Science

spis

Edward Szczypka

23 / 1

Jagiellonian University

Theoretical

Computer Science

Liczby Naturalne – zasada indukcji

Liczby naturalne s ˛

a bardzo wa˙zne w praktyce programistycznej ˝

O s ˛

a u˙zywane do

kodowania (implementowania) danych,

adresowania pami ˛eci,

taktowania programów,

Jedna z podstawowych ich własno´sci jest to, ˙ze do ka˙zdej z nich mo˙zna ¯

ddoj´s´c ˝u zaczynaj ˛

ac od

zera i dodaj ˛

ac 1 odpowiednio wiele razy. Oznacza to, ze

jesli: A ⊆ N jest jakim´s zbiorem liczb naturalnych,

– w którym jest zero

tzn. 0 ∈ Z

– wraz z pocz ˛

atkiem ka˙zdego "kroku"

tzn. ∀k ∈ A k + 1 ∈ A

jest w nim i jego koniec

to: A zawiera juz w sobie WSZYSTKIE liczby naturalne, tzn. A = N.

Edward Szczypka

24 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Przykłady

Przykład 1 Niech zbiór Z składa si ˛e z tych liczb naturalnych n, dla których suma liczb

naturalnych nie przekraczaj ˛

acych n wynosi

n+a

, tzn. spełniaj ˛

acych

0 + 1 + 2 + . . . + n =

n(n + 1)

Czy Z = N? tzn. czy wszystkie liczby naturalne maja powy˙zsza własno´s´c? Oczywi´scie 0 ∈ Z , bo
suma liczb naturalnych nie przekraczaj ˛

acych zera to 0 =

0(0+1)

Nadto, gdy k ∈ Z , tzn.

0 + 1 + 2 + . . . + k =

k (k + 1)

to, badaj ˛

ac, czy k + 1 ∈ Z rozwa˙zamy sum ˛e

0 + 1 + 2 + . . . + k + (k + 1)

(

1 + 2 + 3 + . . . + k ) + (k + 1)

k (k + 1)

+ (

k + 1) =

k (k + 1) + 2(k + 1)

(

k + 1)(k + 2)

(

k + 1)((k + 1) + 1)

co ´swiadczy o tym, ˙ze k + 1 ∈ Z .

Edward Szczypka

25 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Przykłady

Przykład 2

Z =

n ∈ N : 0

+ . . . +

n(n + 1)(2n + 1)

Je´sli poka˙zemy, ze Z = N to dostaniemy ładny wzór na sum ˛e kolejnych kwadratów

Oczywi´scie 0 ∈ Z ,
Nadto, gdy k ∈ Z , to aby stwierdzi´c czy k + 1 jest w Z rozwa˙zamy sum ˛e

+ . . . +

+ (

k + 1)

(

+ . . . +

) + (

k + 1)

k (k + 1)(2k + 1)

+ (

k + 1)

k (k + 1)(2k + 1)

+ (

k + 1)

k (k + 1)(2k + 1) + 6(k + 1)

(

k + 1)(k (2k + 1) + 6(k + 1))

(

k + 1)(2k

7k + 6)

(

k + 1)((k + 2)(2k + 3))

(

k + 1)((k + 1) + 1)(2(k + 1) + 1)))

co ´swiadczy o tym, ˙ze k + 1 ∈ Z .

Edward Szczypka

26 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Przykłady

Przykład 2 Liczenie sumy pot ˛eg kolejnych liczb naturalnych ma bezpo´sredni zwi ˛

azek z praktyka

programistyczna.
Je´sli dla danych wielko´sci k wykonanych musi by´c k

operacji, a w programie jest p ˛etla

wykonuj ˛

aca te operacje dla k = 0, 1, 2, 3, . . . az do n, to ł ˛

acznie wykonanych jest Σ

n
k =0

operacji

Widzieli´smy ju˙z, ˙ze:

n
k =0

n(n + 1)

n
k =0

n(n + 1)(2n + 1)

Edward Szczypka

27 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Sumowanie pot ˛eg liczb naturalnych

Zadanie 3 Poka˙z, ˙ze:

n
k =0

(

n + 1)

n
k =0

n(n + 1)(2n + 1)(3n

3n − 1)

n
k =0

(

n + 1)

(

2n − 1)

n
k =0

n(n + 1)(2n + 1)(3n

− 3n + 1)

n
k =0

(

n + 1)

(

− n

− 4n + 2)

n
k =0

n(n + 1)(2n + 1)(5n

15n

− 15n

− n

9n − 3)

Edward Szczypka

28 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Sumowanie pot ˛eg liczb parzystych

Czasem sumujemy tylko co druga liczb ˛e.
Oczywi´scie sumowanie dla liczb parzystych jest łatwiejsze, bo na przykład:

n
k =0

2k = 2Σ

n
k =0

k = k (k + 1)

n
k =0

(

2k )

4Σ

n
k =0

k =

2n(n + 1)(2n + 1)

n
k =0

(

2k )

8Σ

n
k =0

k = 2n

(

n + 1)

Zadanie 4 Policz;

n
k =0

(

2k )

n
k =0

(

2k )

n
k =0

(

2k )

n
k =0

(

2k )

n
k =0

(

2k )

Edward Szczypka

29 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Sumowanie pot ˛eg liczb nieparzystych

Przykład 5 A ile wynosi suma kolejnych liczb nieparzystych;

n
k =1

(

2k − 1) =?

Oczywi´scie

n
k =1

(

2k − 1) = 2

k = 1nk −

k = 1n1 = 2

n(n + 1)

− n = n(n + 1) − n = n

Przykład 6 Łatwo sprawdzi´c, ze wzór

n
k =1

(

2k − 1)

n(4n

− 1)

zachodzi dla n = 0.
Nadto

n+1
k =1

(

2k − 1)

k = 1n(2k − 1)

+ (

2(n + 1) + 1)

n(4n

− 1)

3(2n + 1)

12n

11n + 3

(

n + 1)(4(n + 1)

− 1))

Edward Szczypka

30 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Sumowanie pot ˛eg liczb nieparzystych

Poza wzorami

n
k =1

(

2k − 1)

n
k =1

(

2k − 1)

n(4n

− 1)

mamy
Zadanie 7 Poka˙z, ˙ze:

n
k =1

(

2k − 1)

(

− 1)

n
k =1

(

2k − 1)

n(4n

− 1)(12n

− 7)

n
k =1

(

2k − 1)

(

16n

− 20n

n
k =1

(

2k − 1)

n(4n

− 1)(48n

− 72n

31)

Edward Szczypka

31 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Modyfikacje

Jesli nasz "marsz"

zamiast od zera zaczniemy od innej liczby a,

ale upewnimy si ˛e, ze zbiór Z ⊆ N, tak jak uprzednio wraz z ka˙zd ˛

a liczb ˛

a k , b ˛edzie zawierał

jej nast ˛epnik k + 1

to mo˙zemy wnioskowa´c, ˙ze w Z s ˛

a wszystkie liczby naturalne pocz ˛

awszy od a, tzn. je´sli

a ∈ Z ⊆ N i ∀k ∈ Z

k + 1 ∈ Z

to Z = {n ∈ N : n a}.

Inna modyfikacja jest zakładanie, ze zbiór Z ⊆ N spełnia:

0 ∈ Z

Z zawiera jak ˛

a´s liczb ˛e, je ˛eli tylko zawiera wszystkie mniejsze od niej

o którym to zbiorze tez mo˙zemy wnioskowa´c, ˙ze Z = N.

Na ogół łatwiej jest wywnioskowa´c, ze k + 1 ∈ Z wiedz ˛

ac, ze 0, 1, 2, . . . , k ∈ Z , ni˙z wiedz ˛

tylko, ˙ze k ∈ Z .

Edward Szczypka

32 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Nierówno ´sci

Mamy przeczucie, ze funkcja n

ro´snie wolniej ni˙z 2

. Co prawda dla pocz ˛

atkowych warto´sci

mamy

. . .

128

256

. . .

i zachowanie tych dwu funkcji nie jest "zdecydowane", ale juz od wi ˛ekszych warto´sci 2

znacznie

dominuje n

. Aby si ˛e przekona´c, ˙ze;

dla n 5

przeprowad´zmy dowód indukcyjny:

Poka˙zemy najpierw, ˙ze 2n + 1 < 2

(dla zupełnie dowolnego n 3)

oczywi´scie 2 · 3 + 1 = 7 < 8 = 2

oraz 2(n + 1) + 1 = 2n + 3 < 2

4 = 2

<¬

2 · 2

n+1

a nast ˛epnie

zauwa˙zmy, ˙ze 5

25 < 32 = 2

oraz, ˙ze (n + 1)

+ (

2n + 1), 2

2 · 2

n+1

Edward Szczypka

33 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Nierówno ´sci

Podobnie, aby pokaza´c, ˙ze:

dla n 10

pokazujemy kolejno, ˙ze:

6n + 6 < 2

ju˙z dla n > 6

to mo˙zna pokaza´c podobnie jak uprzednio 2n + 1 < 2

3n + 1 < 2

dla n 10

jako, ˙ze 3 · 10

3 · 10 + 1 = 331 < 1024 = 210

oraz
3(n + 1)

3(n + 1) + 1 = (3n

3n + 1) + (6n + 6) < 2

2 · 2

n+1

a nast ˛epnie:

nierówno´s´c 10

1000 < 1024 = 2

wraz z (n + 1)

+ (

3n + 1) < 2

n+1

Zadanie 8 Pokaz, ze dla dowolnego wykładnika c mamy

dla dostatecznie du˙zych liczb naturalnych n.

Edward Szczypka

34 / 1

Jagiellonian University

Theoretical

Computer Science

Zasada indukcji – Arytmetyka Modularna

Przykład 9 Poka˙zemy, ze 2|n

− n.

Istotnie 0

− 0 = 0 = 2 · 0, czyli 0

− 0 jest podzielne przez 2.

Nadto, gdy n

− n jest podzielne przez 2 to n

− n = 2x dla pewnej liczby x ∈ N.

A wtedy

(

n + 1)

− (n + 1) = n

2n + 1 − n − 1 = (n

− n) + 2n = 2x + 2n = 2 · (x + n),

co oznacza, ˙ze (n + 1)

− (n + 1) te˙z jest podzielne przez 2.

Przykład 10 Poka˙zemy, ˙ze 6|n

− n.

Istotnie 0

− 0 = 0 = 6 · 0, czyli 0

− 0 jest podzielne przez 6.

Nadto, gdy n

− n jest podzielne przez 6 to n

− n = 6x dla pewnej liczby x ∈ N.

A wtedy
(

n + 1)

− (n + 1) = n

3n + 1 − n − 1 = (n

− n) + 3n

3n = 6x + 3n(n + 1)

Oczywi´scie 3n(n + 1) jest podzielne przez 3. Ale n(n + 1) to iloczyn kolejnych dwu liczb,
wiec która´s z nich, (a zatem i ich iloczyn) musi by´c parzysta.

Oznacza to, ze 3n(n + 1) jest podzielne przez 6, wiec i suma 6x + 3n(n + 1) jest podzielna

przez 6. Czyli, ze (n + 1)2 − (n + 1) te˙z jest podzielne przez 6.

Edward Szczypka

35 / 1

Jagiellonian University

Theoretical

Computer Science