Akademia Górniczo – Hutnicza

im. Stanisława Staszica

w Krakowie

Bartosz Grzesiak

Sławomir Jastrzębski

GiG IV gr. 2 EZSM

Kraków 28.01.2014r.

Wyznaczanie współczynnika oporu rozłożonego.

1.

Wstęp teoretyczny.

Bezwymiarowy współczynnik oporu



zależy od liczby Reynoldsa oraz od chropowatości

względnej



wyrobiska, rozumianej jako stosunek chropowatości bezwzględnej s do promienia

hydraulicznego r

r

s





W wyrobiskach górniczych ruch powietrza jest z reguły turbulentny. Jedynie w

otamowanych wyrobiskach i podsadzanych zrobach spotyka się przepływ laminarny. Wobec tego

współczynnik oporu



dla wyrobisk nie zależy od liczby Reynoldsa, lecz tylko od chropowatości

względnej. Stratę naporu w wentylacji kopalń oblicza się korzystając najczęściej ze współczynnika

oporu



, który wiąże się z bezwymiarowym współczynnikiem oporu przez zależność :







g

8



Współczynnik



zależy nie tylko od chropowatości wyrobiska, ale także od ciężaru

właściwego przepływającego gazu.

W prz

edziale liczb Reynoldsa odpowiadających przepływowi laminarnemu bezwymiarowy

współczynnik oporu nie zależy od chropowatości ścian przewodu. Przy ruchu turbulentnym w

rurach gładkich w szerokim zakresie liczb Reynoldsa współczynnik maleje ze wzrostem liczby

Reynoldsa. W przypadku przewodów chropowatych dla liczb Reynoldsa z przedziału 10

3,6

(duże

chropowatości) – 10

5,8

(małe chropowatości) współczynniki oporu zależą zarówno od

chropowatości względnej, jak też od liczby Reynoldsa.

Celem ćwiczenia jest porównanie wielkości współczynnika oporu przewodów kołowych o

różnej chropowatości i średnicy.

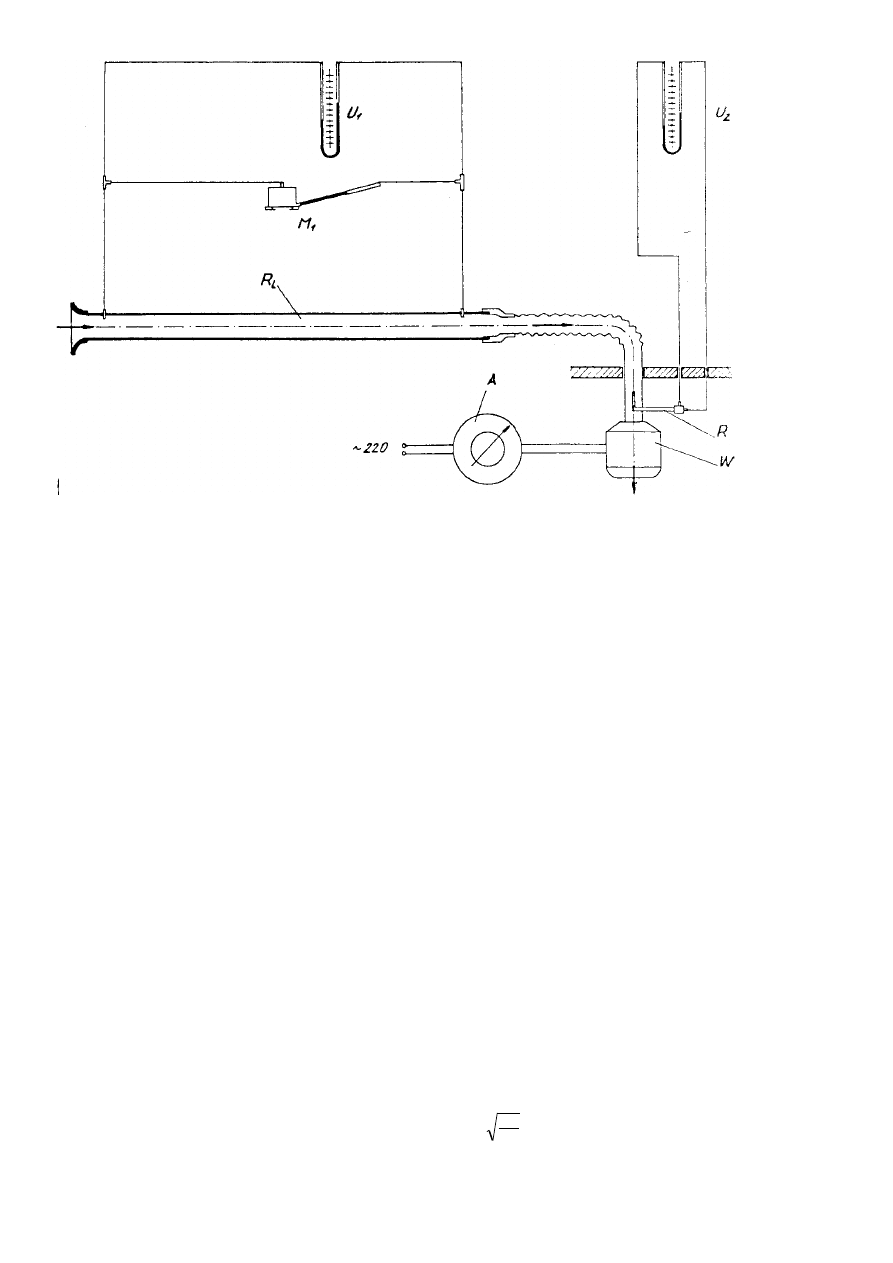
Schemat stanowiska pomiarowego do wyznaczania współczynnika oporu



Stanowisko to jest wyposażone w 3 zestawy rur o różnych średnicach i tej samej długości L

= 1 m. Rury o jednakowej średnicy różnią się chropowatością względną ścianek. Przeprowadzamy

6 pomiarów o różnych prędkościach dla każdej rury. Jak również odczytujemy temperaturę suchą,

wilgotną, ciśnienie barometryczne i gęstość powietrza na stanowisku pomiarowym.

Parametry powietrza na stanowisku:

t

s

= 18,6 [C]

t

m

= 13,6 [C]

p = 987,42 [hPa] = 98742 [Pa]



= 1,17 [kg/m

3

]

2. Wzory obliczeniowe.

W ćwiczeniu tym określamy:

a.

średnią prędkość powietrza w przekroju odcinka pomiarowego:



p

śr

v





2

817

,

0

[m/s]

b.

średnią prędkość w przekroju badanej rury R

1

:

 

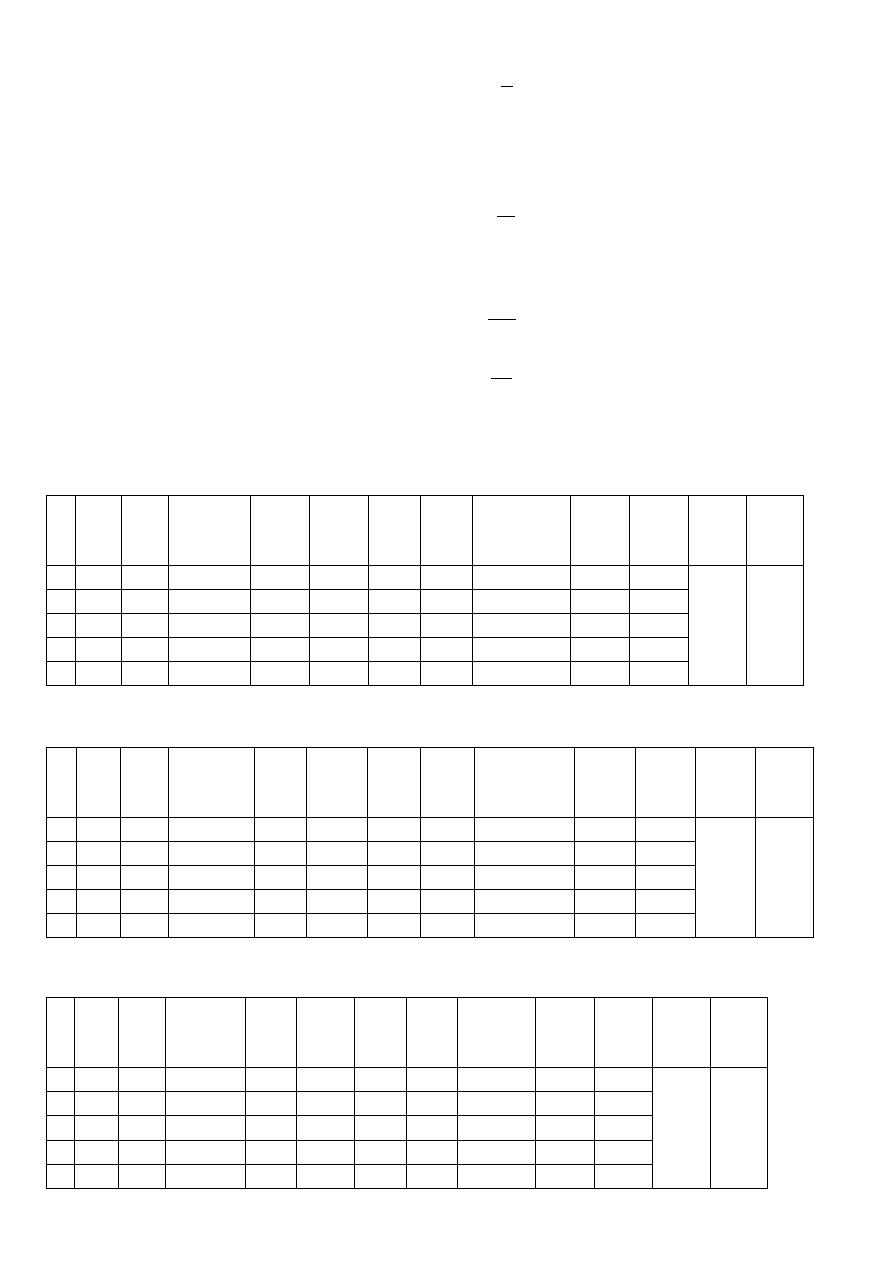
2

30

D

śr

v

v



przyjmując średnice rur: 25, 35, 45 mm

c.

liczbę Reynoldsa:



D

v





Re

d.

współczynnik oporu rozłożonego



i



:







2

2

L

p

D





8

*









3. Obliczenia

Φ25 rura gładka

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

70

53

309,02

519,93

24,36

35,08

58466666,67

0,0107

0,0016

0,0099 0,0014

2

160

62

52

269,28

510,12

24,13

34,75

57916666,67

0,0095

0,0014

3

150

57

48

251,63

470,88

23,18

33,38

55633333,33

0,0097

0,0014

4

140

53

45

233,97

441,45

22,44

32,31

53850000

0,0096

0,0014

5

130

48

40

211,9

392,4

21,16

30,47

50783333,33

0,0098

0,0014

Φ35 rura gładka

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

18

58

79,46

568,98

25,48

18,72

43680000

0,0136

0,0020

0,0139

0,0020

2

160

17

55

75,05

539,55

24,81

18,23

42536666,67

0,0135

0,0020

3

150

16

51

70,63

500,31

23,89

17,55

40950000

0,0137

0,0020

4

140

15

46

66,22

451,26

22,69

16,67

38896666,67

0,0143

0,0021

5

130

13

40

57,36

392,4

21,16

15,55

36283333,33

0,0142

0,0021

Φ45 rura gładka

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

8

60

35,32

588,6

25,92

11,52

34560000

0,0205

0,0030

0,0180

0,0026

2

160

7

55

30,9

539,55

24,81

11,03

33090000

0,0195

0,0029

3

150

6

50

26,49

490,5

23,66

10,52

31560000

0,0184

0,0027

4

140

5

46

22,07

451,26

22,69

10,08

30240000

0,0167

0,0024

5

130

4

41

17,66

402,21

21,42

9,52

28560000

0,0150

0,0022

Φ25 rura średnio chropowata

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

206

52

909,39

459,11

22,89

32,96

54933333,33

0,0358

0,0052

0,0350

0,0051

2

160

190

50

838,76

441,45

22,44

32,31

53850000

0,0343

0,0050

3

150

172

44

759,29

388,48

21,05

30,31

50516666,67

0,0353

0,0052

4

140

155

40

684,25

353,16

20,07

28,9

48166666,67

0,0350

0,0051

5

130

135

35

595,96

309,02

18,78

27,04

45066666,67

0,0348

0,0051

Φ35 rura średnio chropowata

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

33

61

145,68

538,6

24,79

18,21

42490000

0,0263

0,0038

0,0266

0,0039

2

160

30

57

132,44

503,25

23,96

17,6

41066666,67

0,0256

0,0037

3

150

28

52

123,61

459,11

22,89

16,82

39246666,67

0,0261

0,0038

4

140

26

45

114,78

397,31

21,29

15,64

36493333,33

0,0281

0,0041

5

130

22

40

97,12

353,16

20,07

14,75

34416666,67

0,0267

0,0039

Φ45 rura średnio chropowata

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

10

68

44,15

600,37

26,17

11,63

34890000

0,0251

0,0037

0,0213

0,0031

2

160

8

64

35,32

565,06

25,39

11,21

33630000

0,0216

0,0032

3

150

7

56

30,9

494,42

23,75

10,56

31680000

0,0213

0,0031

4

140

6

52

26,49

459,11

22,89

10,17

30510000

0,0197

0,0029

5

130

5

45

22,07

397,31

21,29

9,46

28380000

0,0190

0,0028

Φ25 rura mocno chropowata

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

165

58

728,39

512,08

24,17

34,8

58000000

0,0257

0,0038

0,0251

0,0037

2

160

148

53

653,35

467,94

23,11

33,28

55466666,67

0,0252

0,0037

3

150

135

47

595,96

414,96

21,76

31,33

52216666,67

0,0259

0,0038

4

140

120

44

529,74

388,48

21,05

30,31

50516666,67

0,0246

0,0036

5

130

108

40

476,77

353,16

20,07

28,9

48166666,67

0,0244

0,0036

Φ35 rura mocno chropowata

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

40

62

176,58

547,4

24,99

18,36

42840000

0,0313

0,0046

0,0299

0,0044

2

160

35

57

154,51

503,25

23,96

17,6

41066666,67

0,0298

0,0044

3

150

32

52

141,26

459,11

22,89

16,82

39246666,67

0,0299

0,0044

4

140

29

48

128,02

423,72

21,99

16,16

37706666,67

0,0293

0,0043

5

130

26

43

114,78

379,65

20,81

15,29

35676666,67

0,0294

0,0043

Φ45 rura mocno chropowata

lp

U(V)

m

[mm

alk.]

U2

[mmH2O]

Δp

ST

[Pa]

Δp

d

[Pa]

V

śr

[m/s]

v

[m/s]

Re

λ

α

λ

śr

α

śr

1

170

14

61

61,8

538,57

24,79

11,02

33600000

0,0391

0,0057

0,0337

0,0049

2

160

12

56

52,97

494,42

23,75

10,56

31680000

0,0365

0,0053

3

150

10

50

44,15

441,45

22,44

9,97

29910000

0,0342

0,0050

4

140

8

46

35,32

406,13

21,53

9,57

28710000

0,0297

0,0043

5

130

7

41

30,9

361,99

20,32

9,03

27090000

0,0292

0,0043

4. Wykresy.



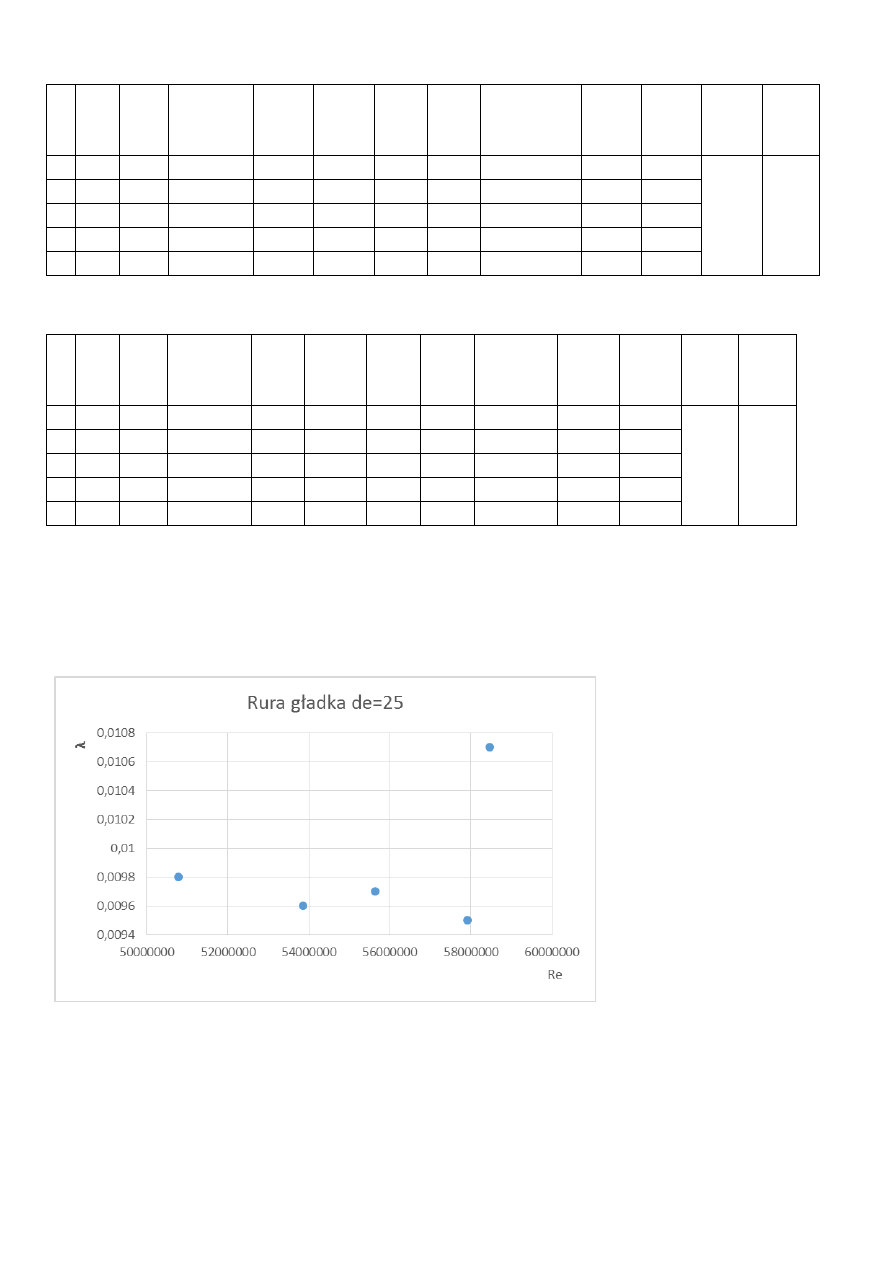
Φ25 rura gładka



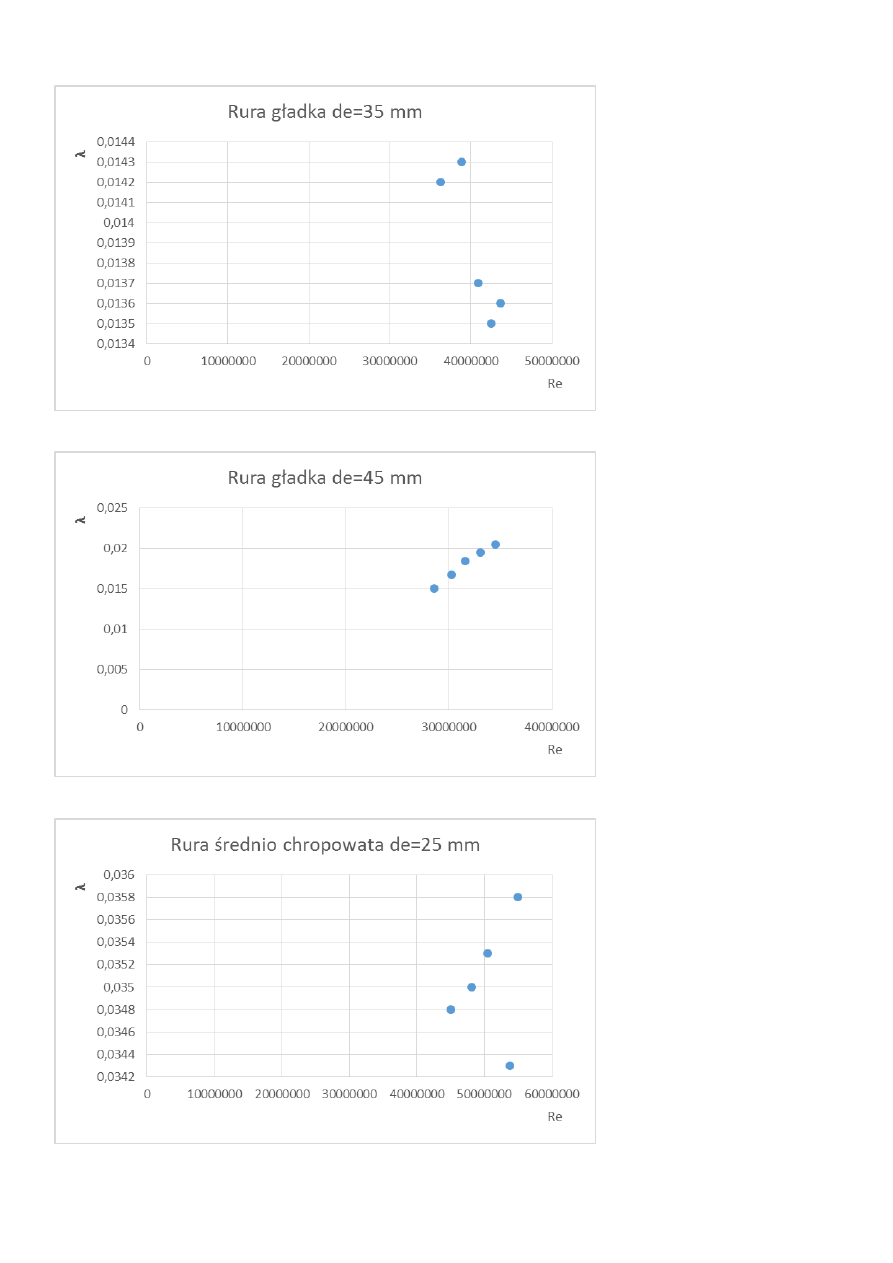
Φ35 rura gładka



Φ45 rura gładka



Φ25 rura średnio chropowata



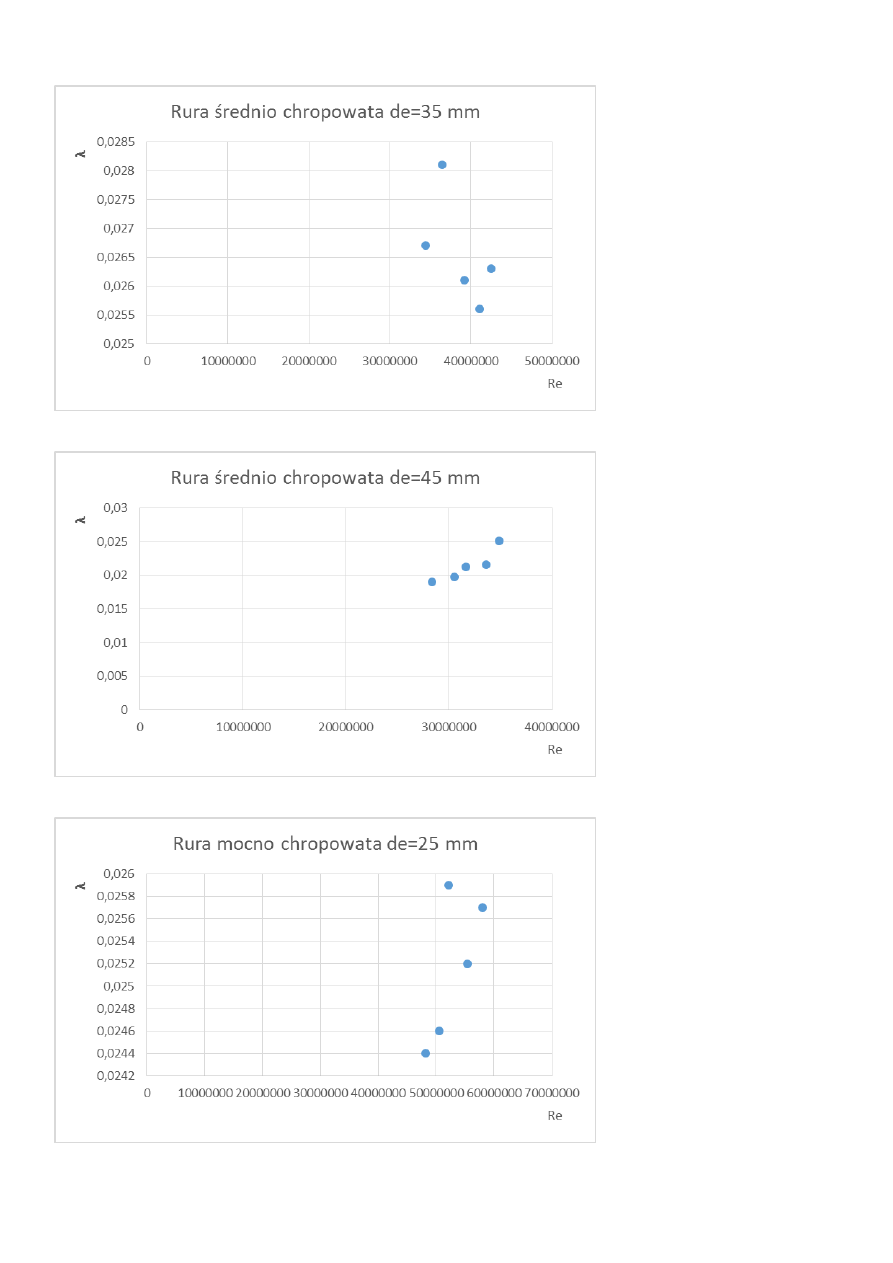
Φ35 rura średnio chropowata



Φ45 rura średnio chropowata



Φ25 rura mocno chropowata



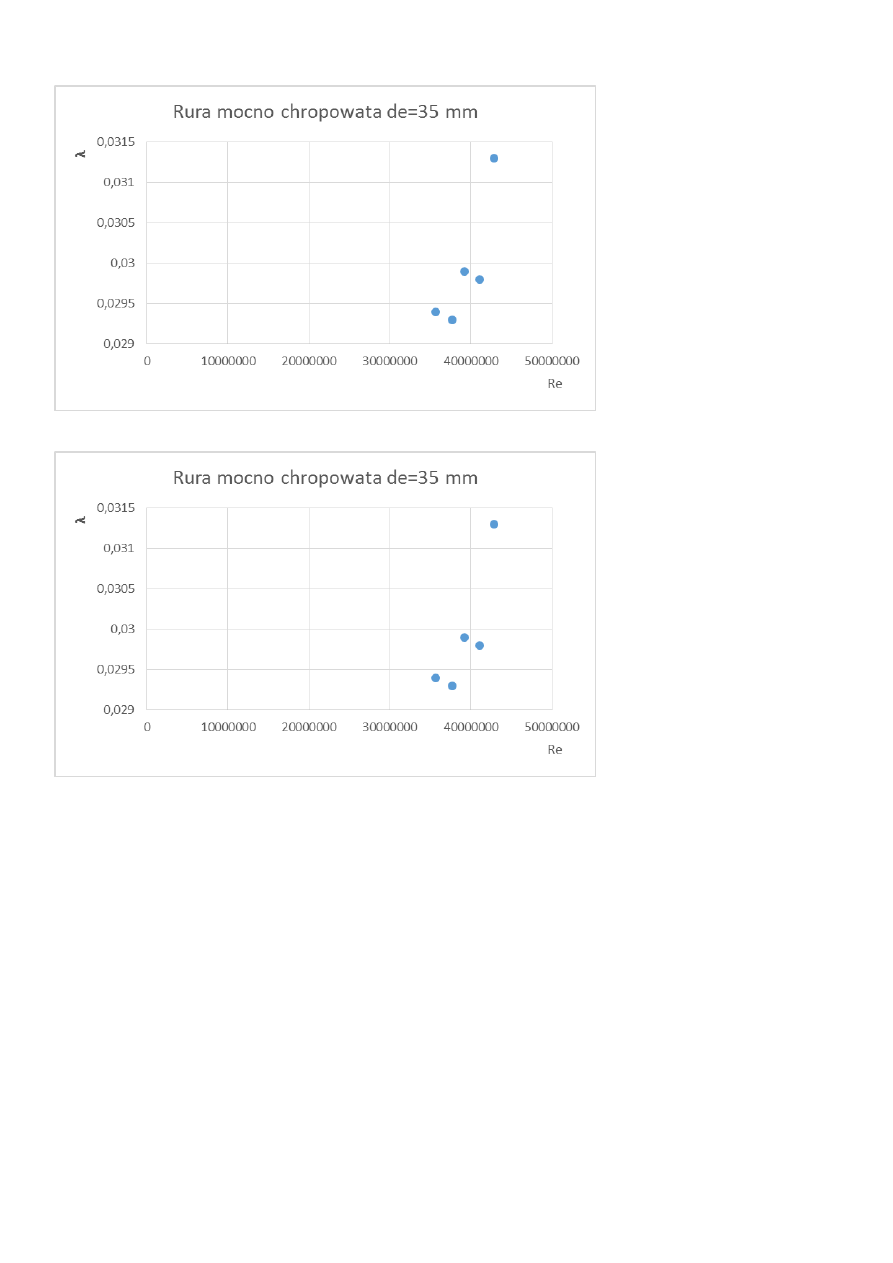
Φ35 rura mocno chropowata



Φ45 rura mocno chropowata

5. Wnioski

Celem ćwiczenia było wyznaczenie współczynnika



oraz współczynnika



aby porównać

wielkości współczynników oporu przewodów kołowych o różnej chropowatości i średnicy.

Po przeprowadzonym doświadczeniu i opracowaniu wyników pomiaru oraz wykonaniu

wykresów można stwierdzić, że podczas przepływu przez przewody prostoosiowe występuje

strata energii wywołana tarciem o ścianki przewodu. Zauważamy również, że bezwymiarowy

współczynnik oporu



zależy od liczby Reynoldsa oraz od chropowatości rury, natomiast

współczynnik oporu



zależy nie tylko od chropowatości, ale także od ciężaru właściwego

przepływającego gazu.

Analizując wykresy dostrzegamy, że im większa średnica tym większa wartość współczynnika



.