Kraków dn. 18.01.2014 r.

Akademia Górniczo-Hutnicza im. Stanisława Staszica

w Krakowie

Wykonali:

Sławomir Jastrzębski
Bartosz Grzesiak
Wydział Górnictwa i Geoinżynierii,
GiG, Rok IV, Grupa 2/1.

2

TEMAT:

WYZNACZANIE

WSPÓŁCZYNNIKA OPORU SKUPIONEGO.

1. Wstęp

Część teoretyczna:

Nie tylko opory ścian, lecz także zmiany pola przekroju (zwiększenie, zwężenie),

zmiany kierunku wyrobiska powodują straty hydrauliczne. Opory odpowiadające tym stratom
nazywają się lokalnymi, miejscowymi lub skupionymi.

Strata naporu wywołana oporami miejscowymi wyraża się zależnością:





2

2

v

w



gdzie:
ξ – współczynnik oporu lokalnego, bezwymiarowy
v – prędkość przepływu powietrza [m/s]
ρ – gęstość powietrza [kg/m

3

]

Współczynnik ξ zależy od rodzaju przepływu, jest proporcjonalny do odwrotności

liczby Reynoldsa przy ruchu laminarnym i nie zależy od tej liczby przy przepływie
turbulentnym. Zależy również od kształtu przeszkody i chropowatości.

Przy obliczeniach dotyczących przepływów ze stałą gęstością można stosować

następujące wzory na opory lokalne wyrobisk:



opór czołowy ciał znajdujących się w prądzie przepływającego powietrza (np. słup
metalowy, drewniany)

3

)

(

732

,

0

c

c

F

F

F

R





gdzie:

F

c

– pole powierzchni czołowej przedmiotu stanowiącego opór

F – pole przekroju poprzecznego przewodu



opór nagłego zwiększenia przekroju z F do F

1

:

2

1

1

1

61

,

0

















F

F

R



opór nagłego zmniejszenia przekroju z F do F

1

:

2

1

1

1

3

,

0

















F

F

R



opór tamy regulacyjnej z otworem F

1

:

2

1

1

1

76

,

1

















F

F

R

3



opór skrętu wyrobiska:

2

1

61

,

0

F

R





Dysponując współczynnikiem oporu lokalnego ξ można określić stratę naporu

wywołaną obecnością oporu. Wobec tego opór lokalny wynosi:

2

2F

R







Schemat pomiarowy:

Na stratę energii między przekrojami pomiarowymi I i II wpływać będzie:

1. strata na oporze lokalnym:

]

/

[

2

3

2

m

J

v

p

m









2. strata na oporze rozłożonym (wywołana tarciem na ścianki przewodu):

]

/

[

2

3

2

m

J

d

Lv

p

L









3. zmiana energii kinetycznej:



2

2

1

1

2

2

2

v

k

v

k

p

K







gdzie:
k

1

,k

2

– współczynniki Coriolisa

v

1

,v

2

– średnie prędkości w przekrojach I i II

Całkowita starta energii miedzy przekrojami będzie równa:

]

/

[

2

2

2

3

2

1

1

2

2

2

2

2

m

J

v

k

v

k

d

Lv

v

p





















Cel ćwiczenia:

Celem ćwiczenia jest doświadczalne określenie wielkości współczynnika oporu

lokalnego, w zależności od prędkości przepływu powietrza, przy nagłym zmniejszeniu i
zwiększeniu przewodu o stałej średnicy.

Przebieg ćwiczenia:

Ćwiczenie polegało na pomiarze, przy pięciu różnych prędkościach przepływu

powietrza, spadków ciśnienia na 3 U-rurkach: U

1

, U

2

i U

3

, dla poszczególnych elementów

oporu.

4

2. Zestawienie wyników pomiarów i obliczenia.

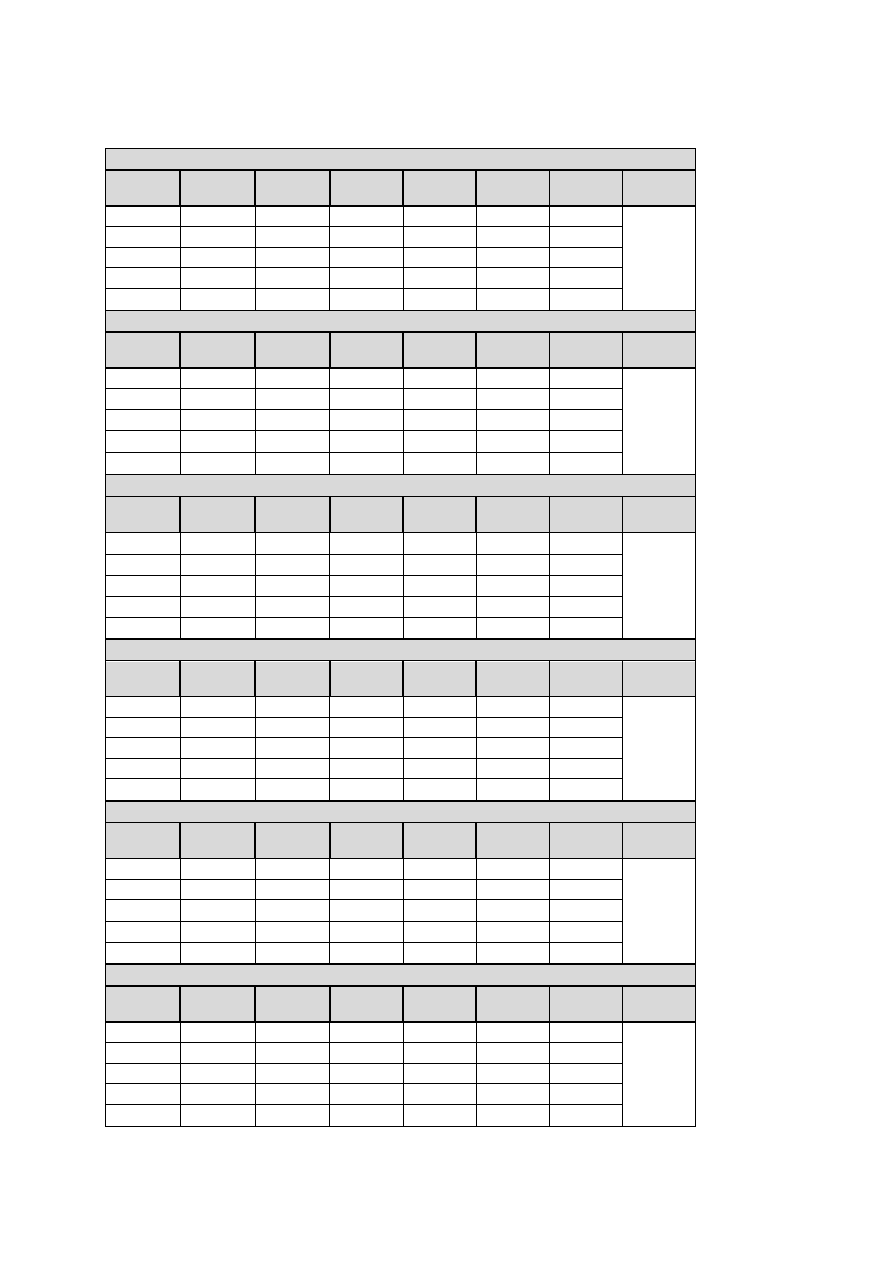
Wartości zmierzone:

U(V)

U1

[mmH

2

O]

U2

[mmH

2

O]

U3

[mmH

2

O]

de=10 mm

150

600

600

20

145

580

580

20

140

560

560

20

135

540

540

20

130

510

510

20

de=15 mm

150

410

410

60

145

390

390

60

140

360

360

60

135

330

330

60

130

310

310

60

de=20 mm

150

200

200

120

145

180

180

110

140

170

170

100

135

160

160

100

130

150

150

100

de=25 mm

150

90

90

150

145

80

80

140

140

70

70

130

135

65

65

120

130

60

60

110

de=30 mm

150

35

35

160

145

30

30

150

140

30

30

140

135

25

25

135

130

25

25

120

de=40 mm

150

10

10

170

145

5

5

155

140

5

5

150

135

5

5

140

130

5

5

130

5

3.Obliczenia:

Przesłona de = 10 mm

Δp1

[N/m2]

Δp2

[N/m2]

Δp3

[N/m2]

Vśr [m/s]

V [m/s]

ξ

dc/D

ξ

Śr.

5886

5886

196,2

14,8358

0,7326

18431,87 0,222222

17141,63

5689,8

5689,8

196,2

14,8358

0,7326

17817,47 0,222222

5493,6

5493,6

196,2

14,8358

0,7326

17203,08 0,222222

5297,4

5297,4

196,2

14,8358

0,7326

16588,68 0,222222

5003,1

5003,1

196,2

14,8358

0,7326

15667,09 0,222222

Przesłona de = 15 mm

Δp1

[N/m2]

Δp2

[N/m2]

Δp3

[N/m2]

Vśr [m/s]

V [m/s]

ξ

dc/D

ξ

Śr.

4022,1

4022,1

588,6

25,6964

2,8551

829,26

0,333333

728,13

3825,9

3825,9

588,6

25,6964

2,8551

788,81

0,333333

3531,6

3531,6

588,6

25,6964

2,8551

728,13

0,333333

3237,3

3237,3

588,6

25,6964

2,8551

667,45

0,333333

3041,1

3041,1

588,6

25,6964

2,8551

627,00

0,333333

Przesłona de = 20 mm

Δp1

[N/m2]

Δp2

[N/m2]

Δp3

[N/m2]

Vśr [m/s]

V [m/s]

ξ

dc/D

ξ

Śr.

1962

1962

1177,2

36,3403

7,1783

63,99

0,444444

62,22

1765,8

1765,8

1079,1

34,7932

6,8727

62,83

0,444444

1667,7

1667,7

981

33,1740

6,5528

65,27

0,444444

1569,6

1569,6

981

33,1740

6,5528

61,43

0,444444

1471,5

1471,5

981

33,1740

6,5528

57,59

0,444444

Przesłona de = 25 mm

Δp1

[N/m2]

Δp2

[N/m2]

Δp3

[N/m2]

Vśr [m/s]

V [m/s]

ξ

dc/D

ξ

Śr.

882,9

882,9

1471,5

40,6297

12,5400

9,43

0,555556

8,79

784,8

784,8

1373,4

39,2520

12,1148

8,98

0,555556

686,7

686,7

1275,3

37,8242

11,6741

8,46

0,555556

637,65

637,65

1177,2

36,3403

11,2161

8,51

0,555556

588,6

588,6

1079,1

34,7932

10,7386

8,57

0,555556

Przesłona de = 30 mm

Δp1

[N/m2]

Δp2

[N/m2]

Δp3

[N/m2]

Vśr [m/s]

V [m/s]

ξ

dc/D

ξ

Śr.

343,35

343,35

1569,6

41,9621

18,6498

1,65

0,666667

1,55

294,3

294,3

1471,5

40,6297

18,0576

1,51

0,666667

294,3

294,3

1373,4

39,2520

17,4453

1,62

0,666667

245,25

245,25

1324,35

38,5447

17,1309

1,40

0,666667

245,25

245,25

1177,2

36,3403

16,1512

1,58

0,666667

Przesłona de = 40 mm

Δp1

[N/m2]

Δp2

[N/m2]

Δp3

[N/m2]

Vśr [m/s]

V [m/s]

ξ

dc/D

ξ

Śr.

98,1

98,1

1667,7

43,2536

34,1756

0,14

0,888889

0,09504

49,05

49,05

1520,55

41,3013

32,6331

0,0774

0,888889

49,05

49,05

1471,5

40,6297

32,1024

0,0799

0,888889

49,05

49,05

1373,4

39,2520

31,0139

0,0857

0,888889

49,05

49,05

1275,3

37,8242

29,8857

0,0922

0,888889

6

Zmierzone parametry na stanowisku:

Temperatura sucha:

C

t

o

s

6

,

18



Temperatura wilgotna:

C

t

o

w

6

,

13



Ciśnienie barometryczne:

Pa

p

98742



Gęstość powietrza:

3

19

,

1

m

kg





Obliczenia:

1. Przeliczanie jednostek ciśnienia na z mmH

2

O na Pa

x

x

gU

p



gdzie:
U

x

– wartość pomierzona

g – przyspieszenie ziemskie, g= 9,81 [m/s

2

]

2. Gęstość powietrza, ze wzoru:

]

/

[

19

,

1

)

378

,

0

(

003484

,

0

3

m

kg

p

p

T

w

w









gdzie:
T

w

=273+13,6=286,6 K

p – ciśnienie barometryczne
p

w

– prężność pary wodnej

p

wn

=2482[Pa]

]

[

04

,

2155

)

(

10

*

6225

,

6

4

Pa

p

t

t

p

p

w

s

wn

w











3. Średnia prędkość powietrza:

]

/

[

2

817

,

0

3

s

m

p

v

śr





4. Średnia prędkość w przekroju I-IV

]

/

[

444

,

0

2

s

m

v

D

d

v

v

śr

śr

















D=45mm

7

5. Współczynnik oporu skupionego





2

1

2

2

2

v

p

p









4.Wykresy:



)

(v

f





15500

16000

16500

17000

17500

18000

18500

19000

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

de=10

0

100

200

300

400

500

600

700

800

900

0

0,5

1

1,5

2

2,5

3

de=15mm

8

57

58

59

60

61

62

63

64

65

66

6,5

6,6

6,7

6,8

6,9

7

7,1

7,2

7,3

de=20mm

8,4

8,6

8,8

9

9,2

9,4

9,6

10,5

11

11,5

12

12,5

13

de=25mm

1,35

1,4

1,45

1,5

1,55

1,6

1,65

1,7

16

16,5

17

17,5

18

18,5

19

de=30mm

9

















D

d

f

e



5.Wnioski

Im mniejsza jest średnica przeszkody, tzn. im większe jest zwężenie

przewodu, tym większy jest współczynnik oporu lokalnego ξ, co wiąże się z
tym, że straty lokalne przepływu powietrza dla danego przekroju rosną.

0

0,02

0,04

0,06

0,08

0,1

0,12

0,14

0,16

29

30

31

32

33

34

35

de=40mm

0

2000

4000

6000

8000

10000

12000

14000

16000

18000

0

0,2

0,4

0,6

0,8

1

f(de/D)