
Politechnika Warszawska
Instytut Automatyki i Robotyki
Prof. dr hab. inż. Jan Maciej Kościelny
PODSTAWY AUTOMATYKI
PODSTAWY AUTOMATYKI
część 4
Schematy blokowe
2
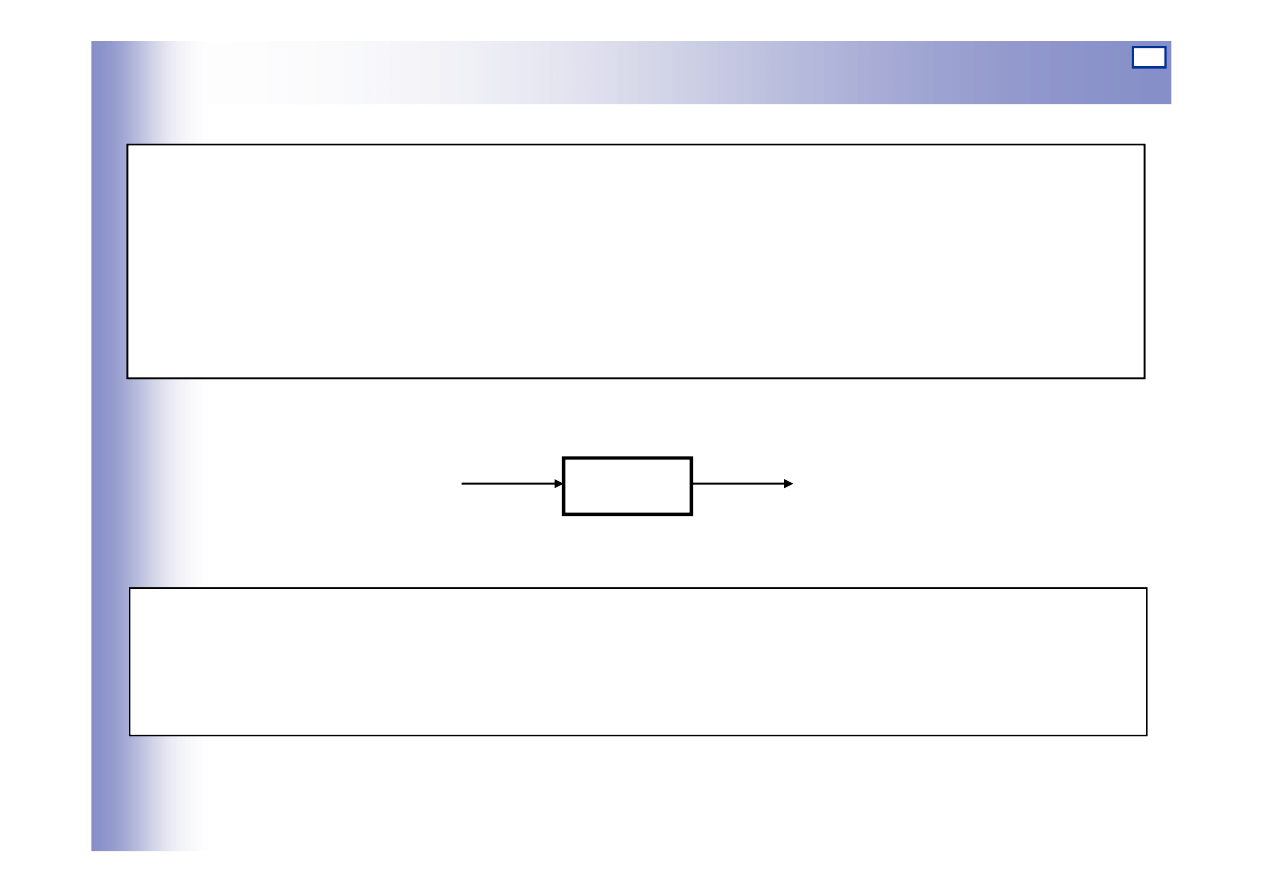
Schemat blokowy
Schematy blokowe (strukturalne): przedstawiają wzajemne powiązania
pomiędzy poszczególnymi zespołami analizowanego elementu
lub układu, tzn. podają kierunki przepływu sygnałów oraz związki
między sygnałami wejściowymi i wyjściowymi wszystkich
zespołów.
Na schemacie blokowym nie przedstawia się konstrukcji poszczególnych
elementów układu, a jedynie ich ogólne własności i wzajemne
powiązania między poszczególnymi elementami
G(s)
y
u
3
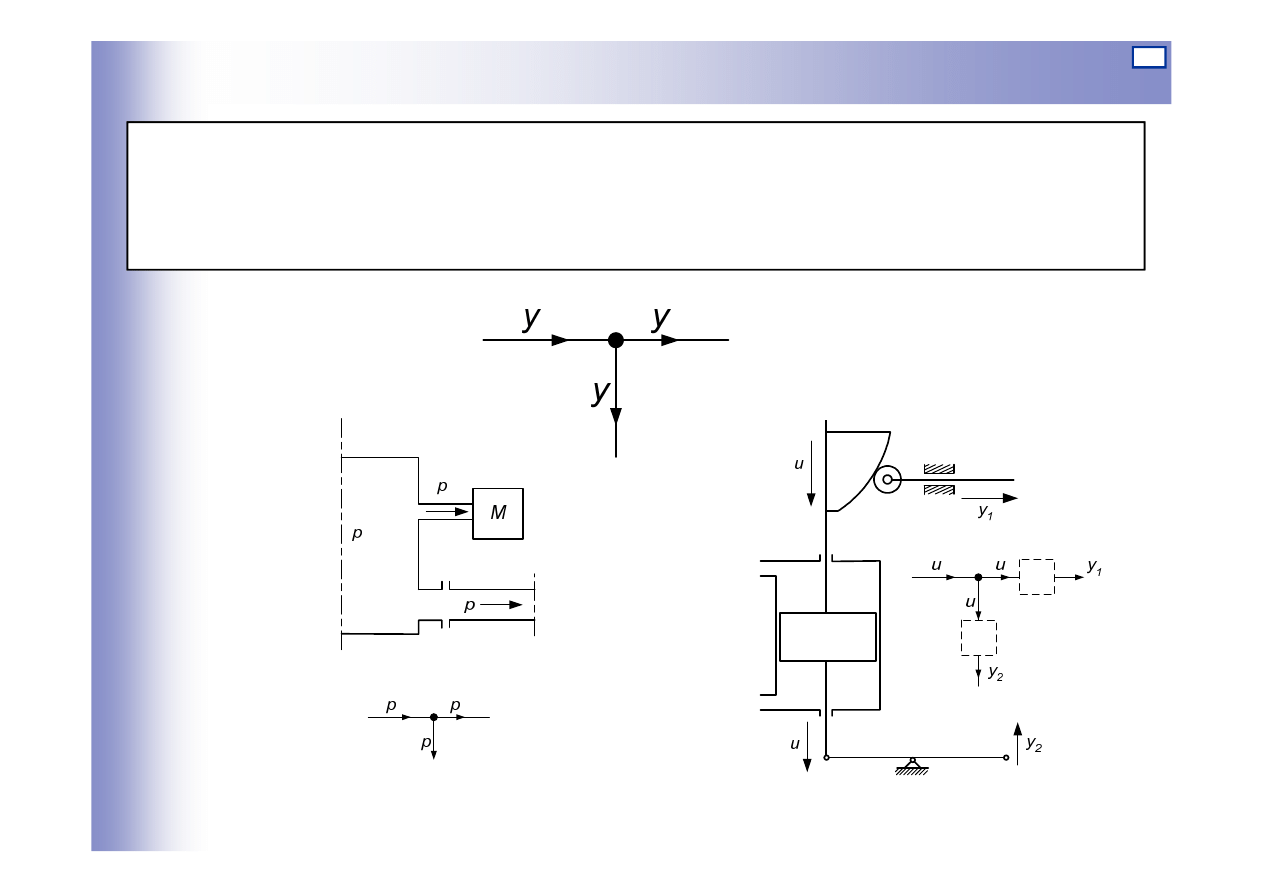
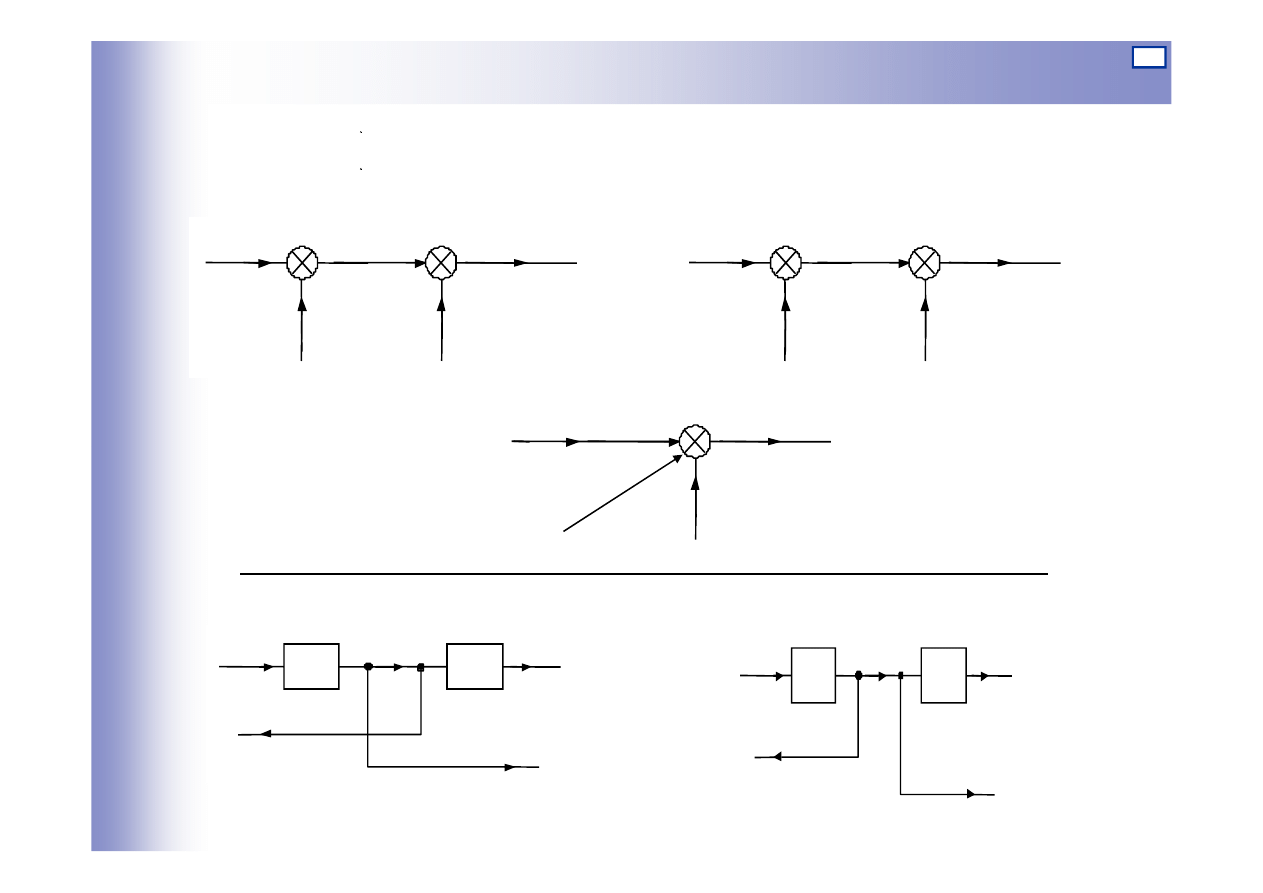
Węzły informacyjne
Węzły informacyjne (zaczepowe): reprezentują na schematach
blokowych urządzenia, które pozwalają pobierać tę samą
informację do kilku gałęzi układu
4
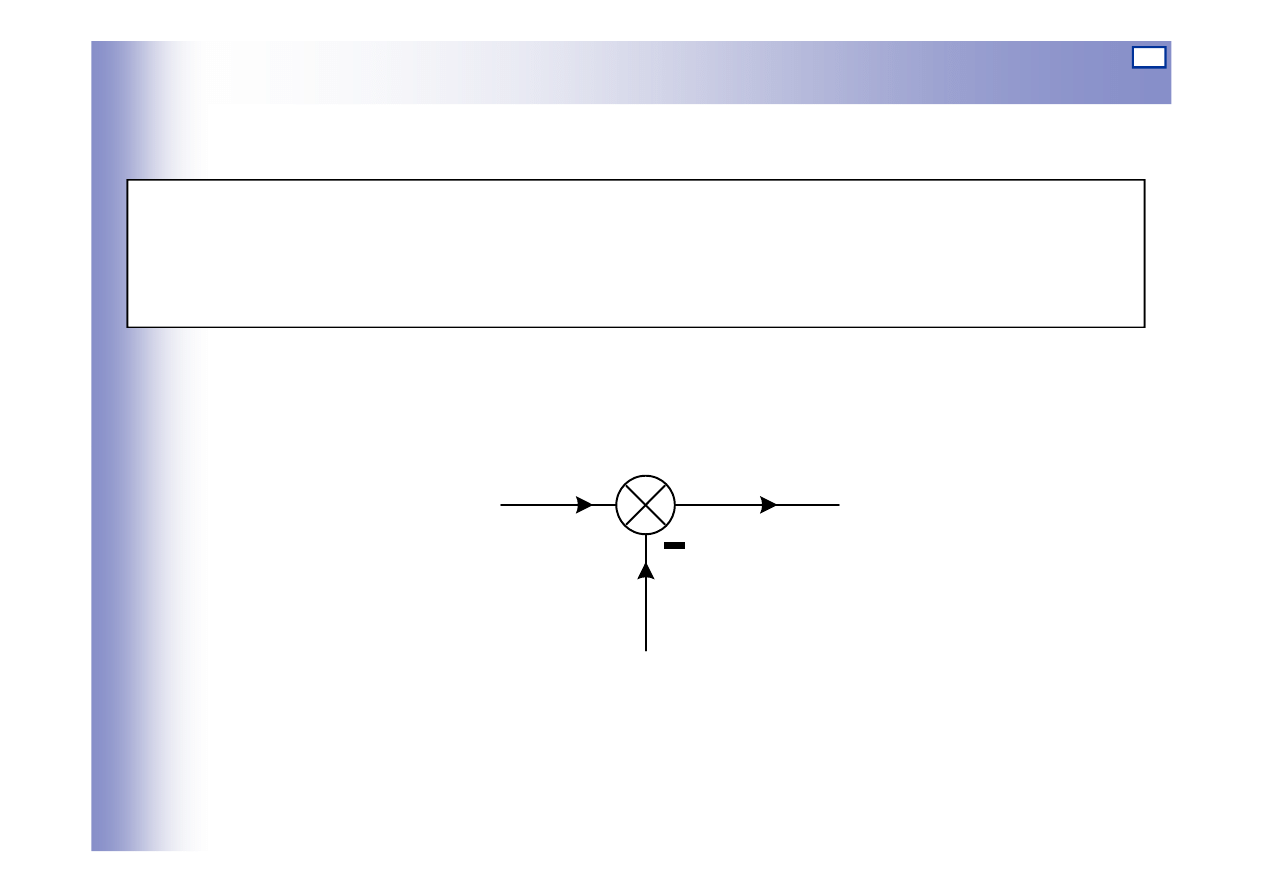
Węzły sumacyjne
Węzły sumacyjne: reprezentują na schematach blokowych urządzenia, w
których zachodzi algebraiczne (z uwzględnieniem znaków)
sumowanie sygnałów
z
u
+
y
z=u-y
5
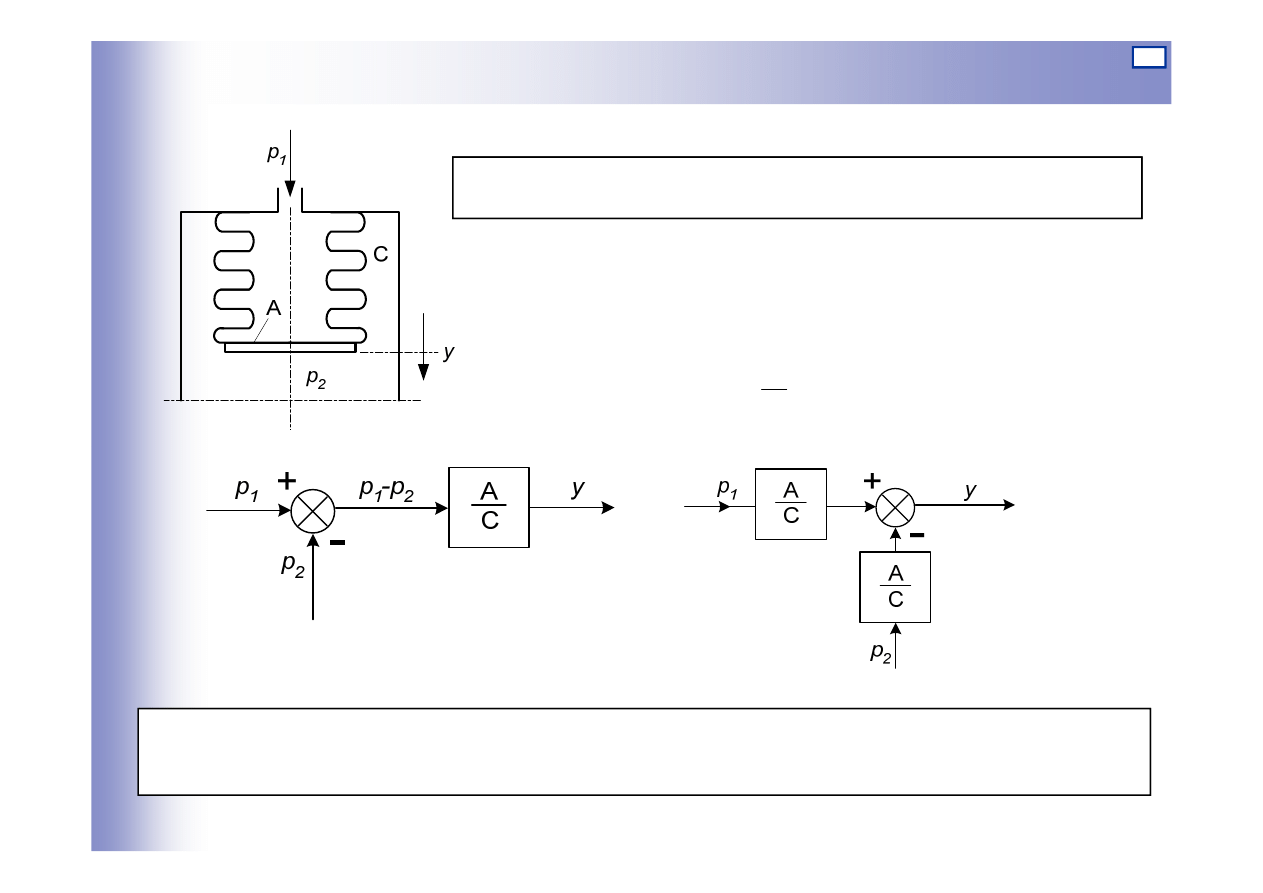
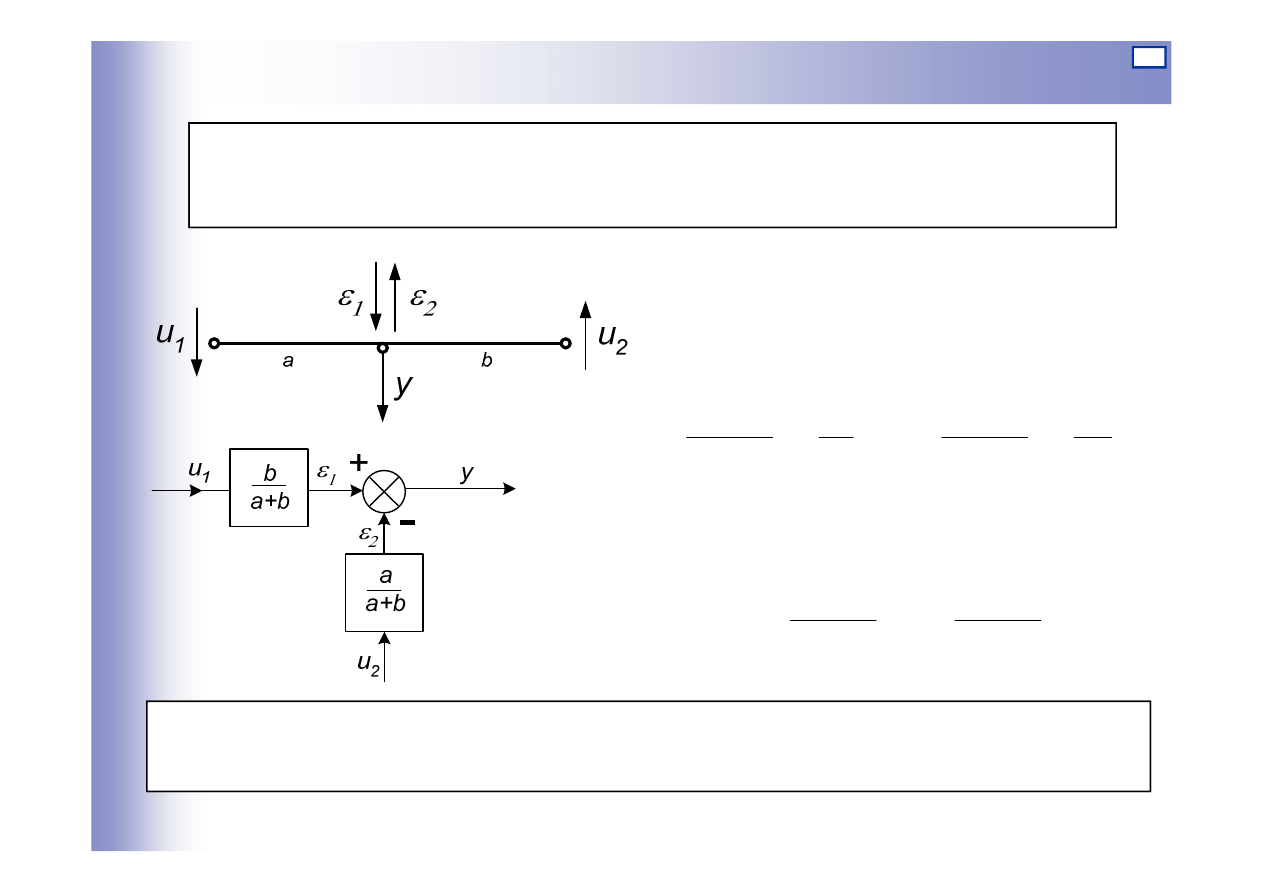
Węzły sumacyjne – przykład 1
)
(
)
(
2
1
2
1
p
p
c
A
y
cy
A
p
p
−
=
=
−
c
Równanie sił działających na mieszek sprężysty:
Gdzie:
p1,p2 – sygnały wejściowe (ciśnienia); y – sygnał wyjściowy (przesunięcie);
A – powierzchnia efektywna mieszka sprężystego; C - sztywność mieszka;
6
Węzły sumacyjne – przykład 2
2
2
1
1
2
1
a
b
a
u
b
b
a
u
y
=
+
=
+
−
=
c
ε
ε
ε
ε
Dźwignia: przy małych przemieszczeniach u
1
i u
2
zgodnie z zasadą
superpozycji można zapisać:
2
1
u
b
a
a
u
b
a
b
y
a
b
a
b
b
a
+
−
+
=
=
+
=
+
c
Gdzie: u
1
, u
2
–
sygnały wejściowe (przesunięcia); y – sygnał wyjściowy
(przesunięcia);
ε
1
,
ε
2
– składowe przesunięcia y; a, b – ramiona dźwigni
7
Przekształcenia schematów blokowych
Aby wyznaczyć transmitancję całego obiektu na podstawie
schematu blokowego, należy dany schemat strukturalny
przekształcić do najprostszej postaci:
G(s)
y
u
W przypadku dość uwikłanych postaci schematów blokowych
należy w pierwszej kolejności dokonać takich uproszczeń, aby
występowały tylko schematy połączeń:
•
szeregowych
•
równoległych
•
ze sprzężeniem zwrotnym
8
Przekształcenia schematów blokowych
Połączenia szeregowe:
G
1
(s)
G
2
(s)
y
1
u
y
)
(
)
(
)
(
)
(
)
(
)
(
1
2
1
1
s
y
s
G
s
y
s
u
s
G
s
y
=
=
c
G(s)
y
u
)
(
)
(
)
(
)
(
1
2
s
u
s
G
s
G
s
y
=
c
∏
=
=
n
i
i
s
G
s
G
1
)
(
)
(
Uwaga:
Dla elementów wielowymiarowych G(s) i G
i
(s) są macierzami
transmitancjami i nie wolno zmieniać kolejności w iloczynie macierzy
9
Przekształcenia schematów blokowych
Połączenia równoległe:
G(s)
y
u
G
1
(s)
G
2
(s)
u
y
1
y
2
y
+
-
G(s)
)
(
))
(
)
(
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
1
2
2
1
1
s
u
s
G
s
G
s
y
s
y
s
y
s
u
s
G
s
y
s
u
s
G
s
y
−
=
−
=
=
=
c
∑
=
=
n
i
i
s
G
s
G
1
)
(
)
(
10
Przekształcenia schematów blokowych
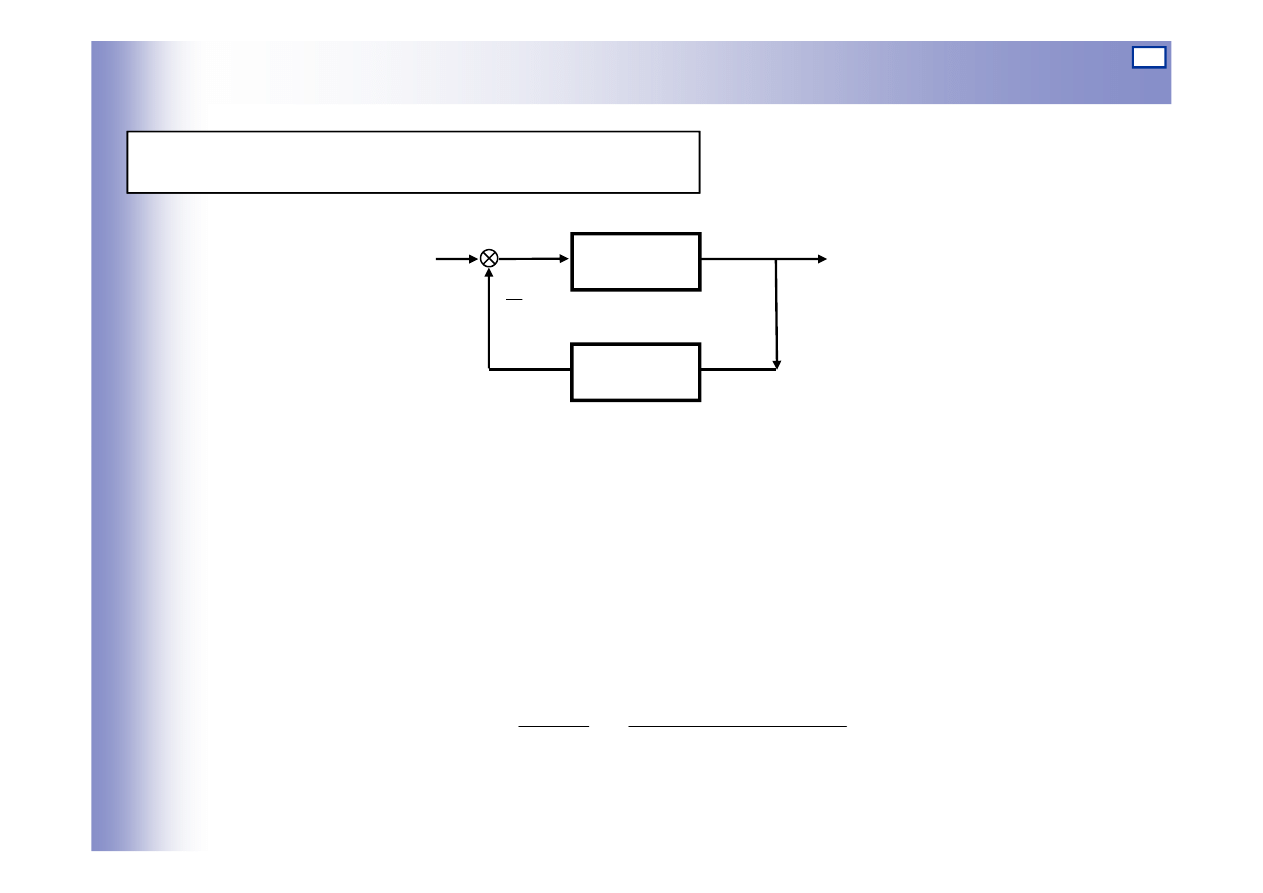
Połączenia ze sprzężeniem zwrotnym:
)
(
)
(
)
(
)
(
)
(
)
(
±
=
=
G
1
(s)
G
2
(s)
u
y
1
y
+
v
)
(
)
(
1
)
(
)
(
)
(
)
(
)]
(
)
(
)
(
)[
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
1
2
1
2
1
1
1
s
G
s
G
s
G
s
u
s
y
s
G
s
y
s
G
s
u
s
G
s
y
s
y
s
G
s
y
s
y
s
u
s
v
s
v
s
G
s
y
m
c
=
=
±
=
=
±
=
=
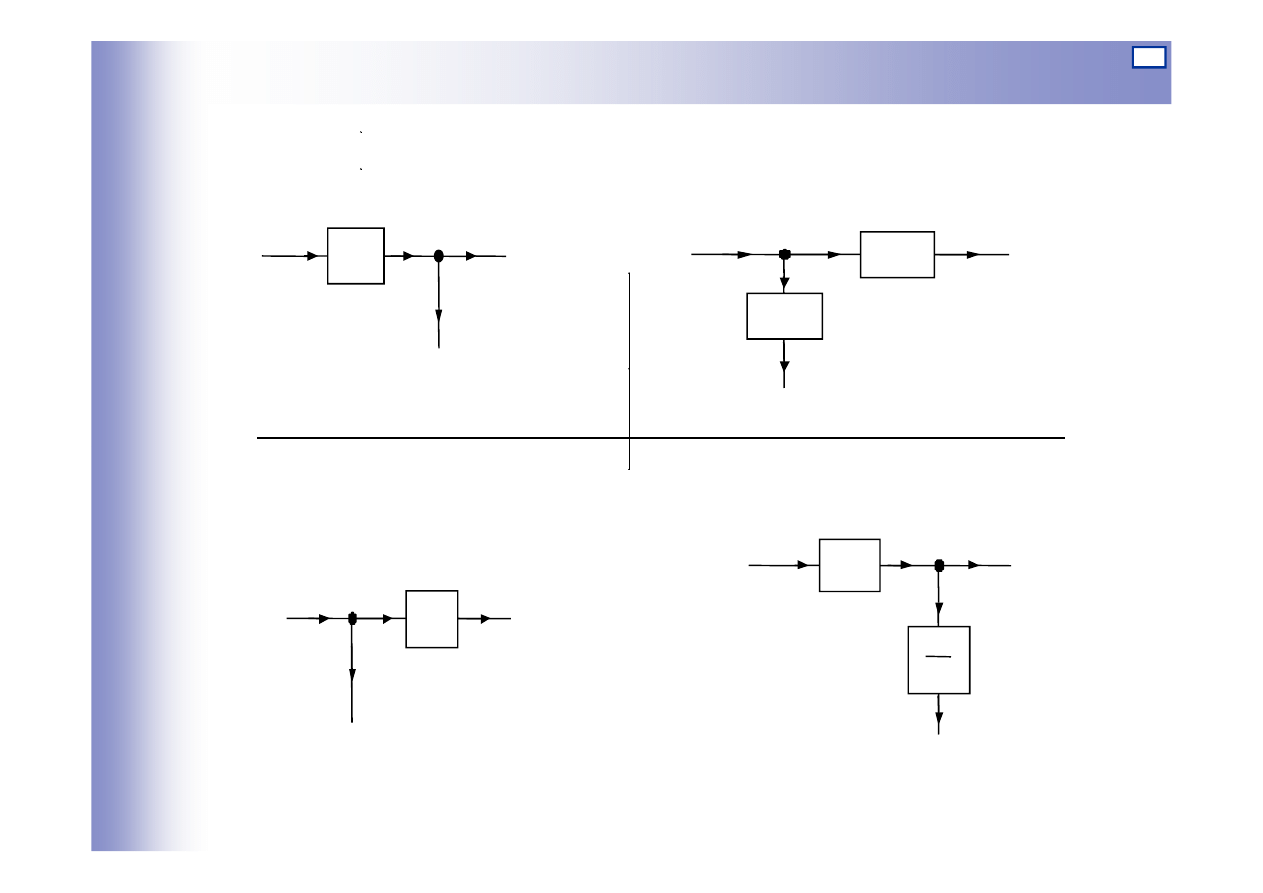
11
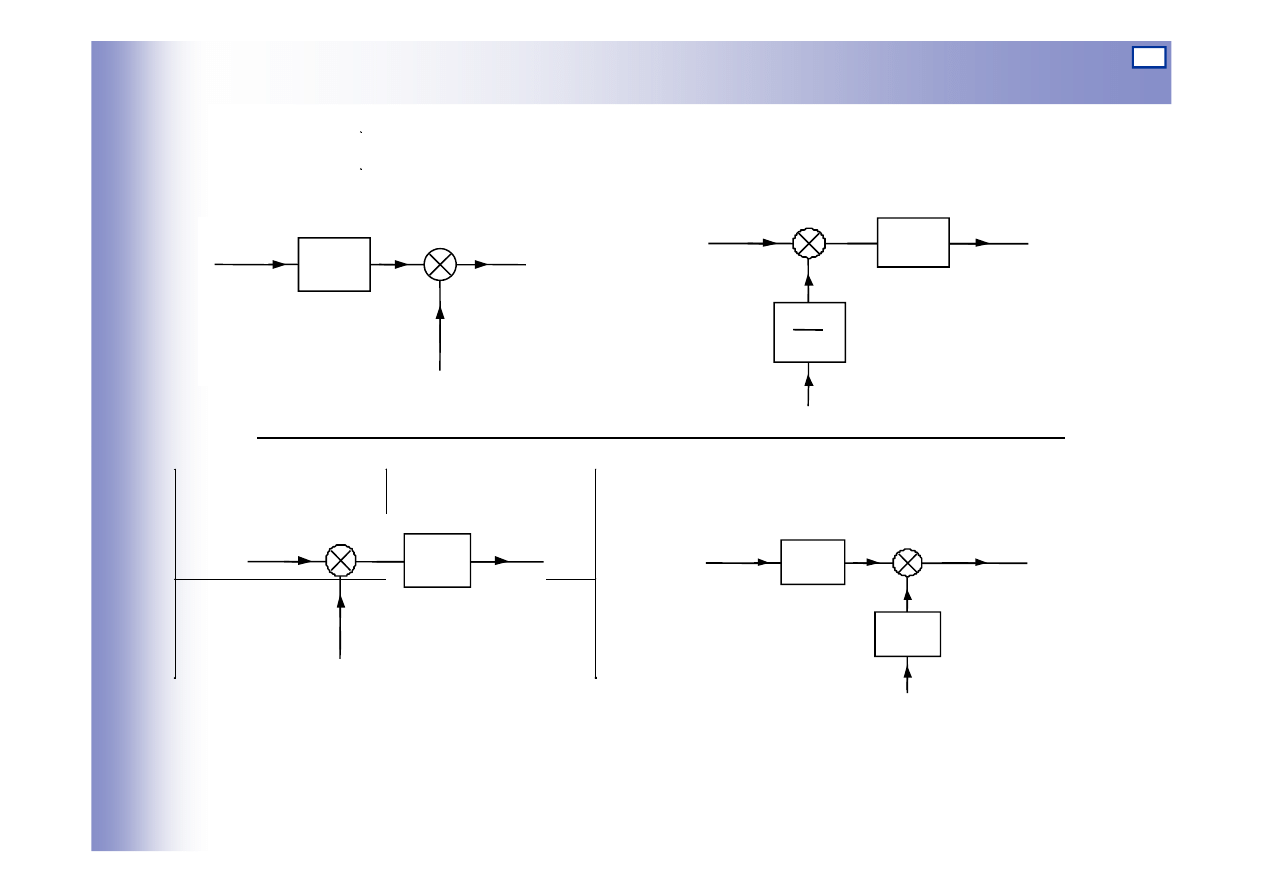
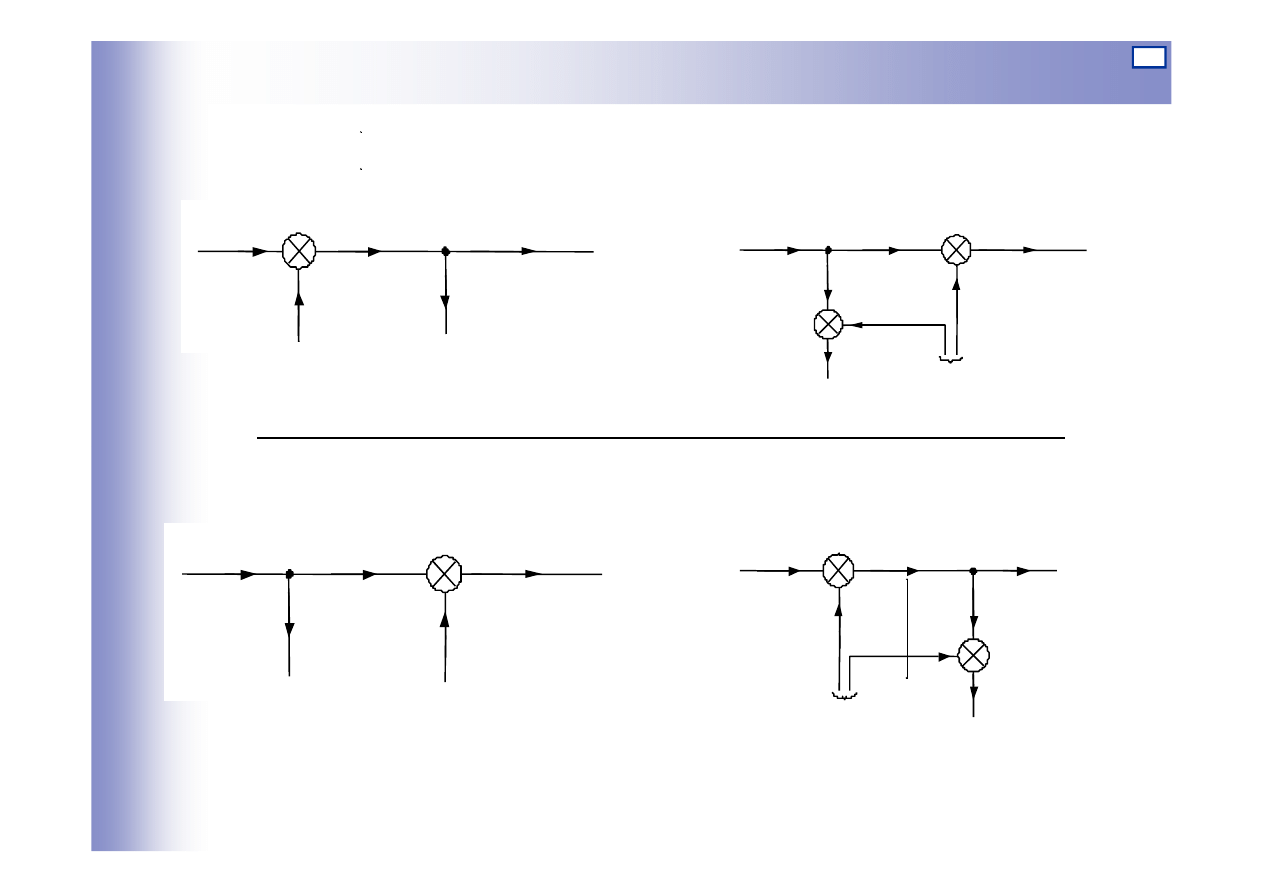
Przesunięcia węzłów informacyjnych i sumacyjnych
u
y
y
G
u
y
y
G
G
Schemat równoważny
Schemat pierwotny
u
y
u
G
u
y
u
G
1
G
12
Przesunięcia węzłów informacyjnych i sumacyjnych
Schemat równoważny
Schemat pierwotny
-
u
1
y
G
+
u
2
-
y
G
+
1
G
u
2
u
1
-
y
G
+
u
1
u
2
-
y
G
+
G
u
1
u
2
13
Przesunięcia węzłów informacyjnych i sumacyjnych
Schemat równoważny
Schemat pierwotny
-
u
1
y
u
2
+
+
+
u
1
- u
2
u
3
y=u
1
- u
2
+u
3
-
u
1
y
u
2
+
+
+
u
1
+ u
3
u
3
y=u
1
+ u
3
-u
2
u
1
y
+
+
u
y
1
y
2
G
1
G
2
y
2
y
1
u
G
1
G
2
y
1
y
2
y
1
y
2
-
u
2
+
u
3
y=u
1
- u
2
+u
3
14
Przesunięcia węzłów informacyjnych i sumacyjnych
Schemat równoważny
Schemat pierwotny
u
1
y
u
2
+
-
y
y=u
1
-u
2
y
+
-
y
+
-
u
1
u
2
y=u
1
-u
2
y
+
-
u
1
u
1
u
2
y=u
1
-u
2
y
+
-
+
+
y=u
1
-u
2
u
1
u
1
u
2
-
15
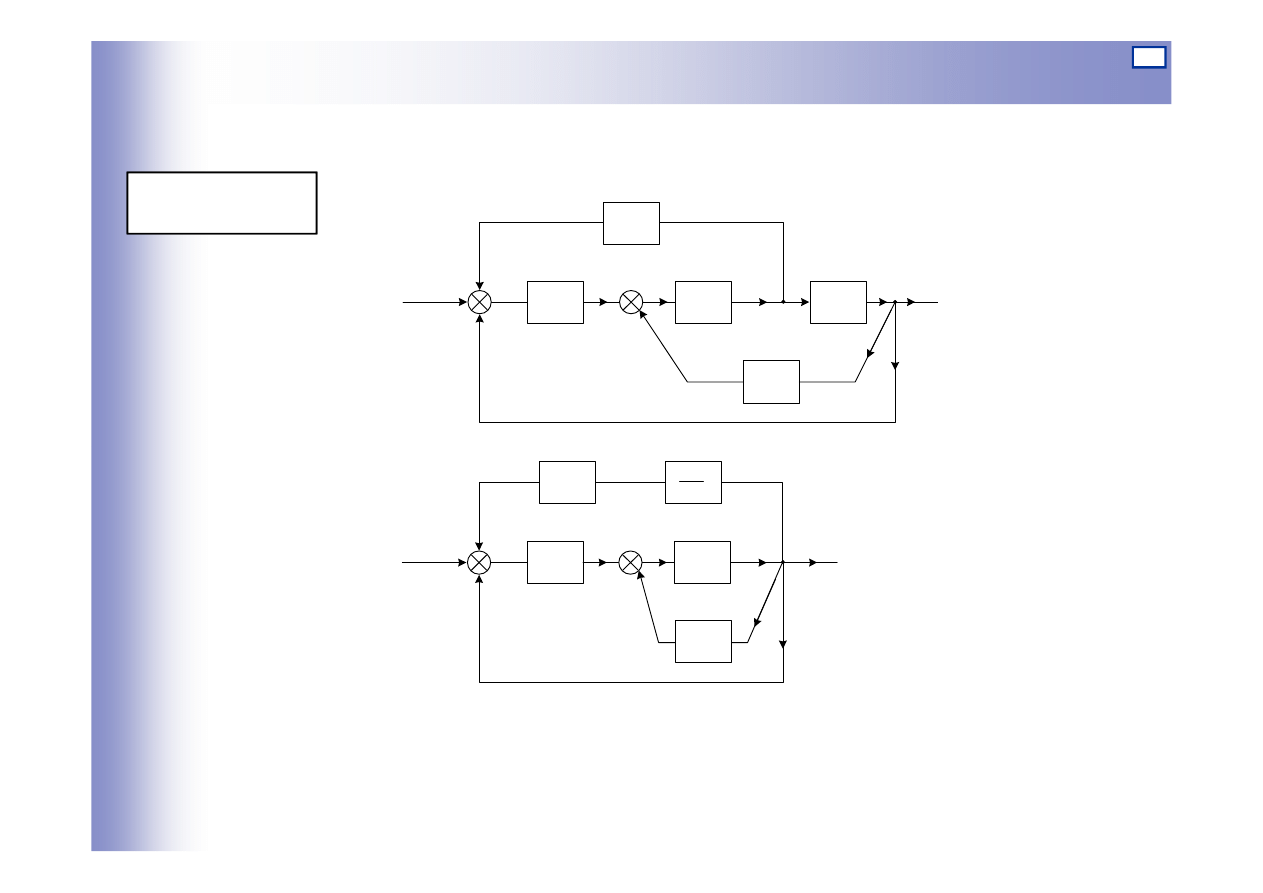
Przekształcenia schematów blokowych – przykład 1
Przykład 1:
+
-
u
G
1
y
G
4
G
2
G
3
G
2
-
+
a)
5
G
+
-
u
G
1
y
G
4
G
2
G
3
G
5
-
+
1
G
3
b)
16
Przekształcenia schematów blokowych – przykład 1
)
(
1
)
(
4
3
2
1
5
3
2
3
2
1
G
G
G
G
G
G
G
G
G
G
s
G
−
+
+
=
17
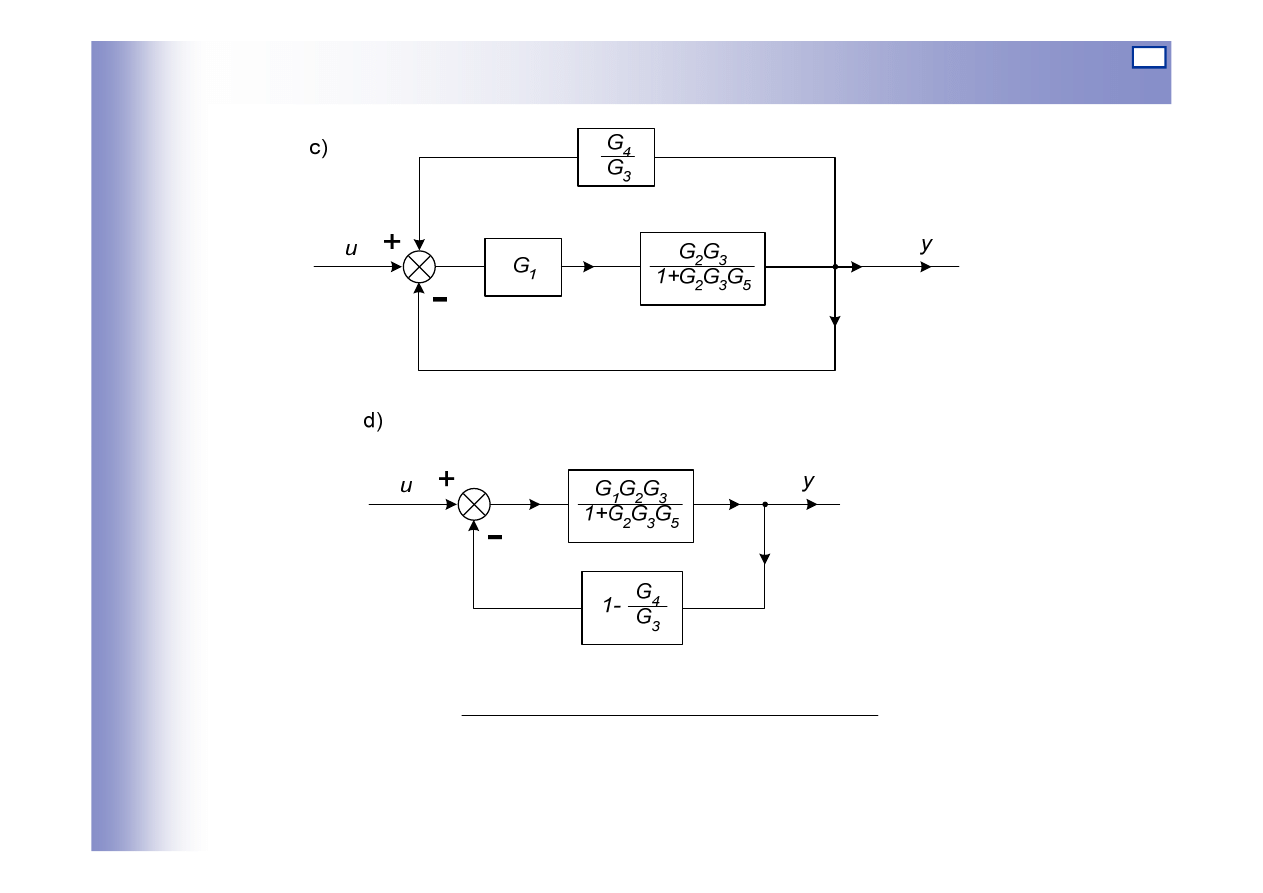
Przekształcenia schematów blokowych – przykład 2
Przykład 2:
G
1
G
2
G
3
G
4
G
5
1/G
2
-
+
+
+
-
b)
-
y
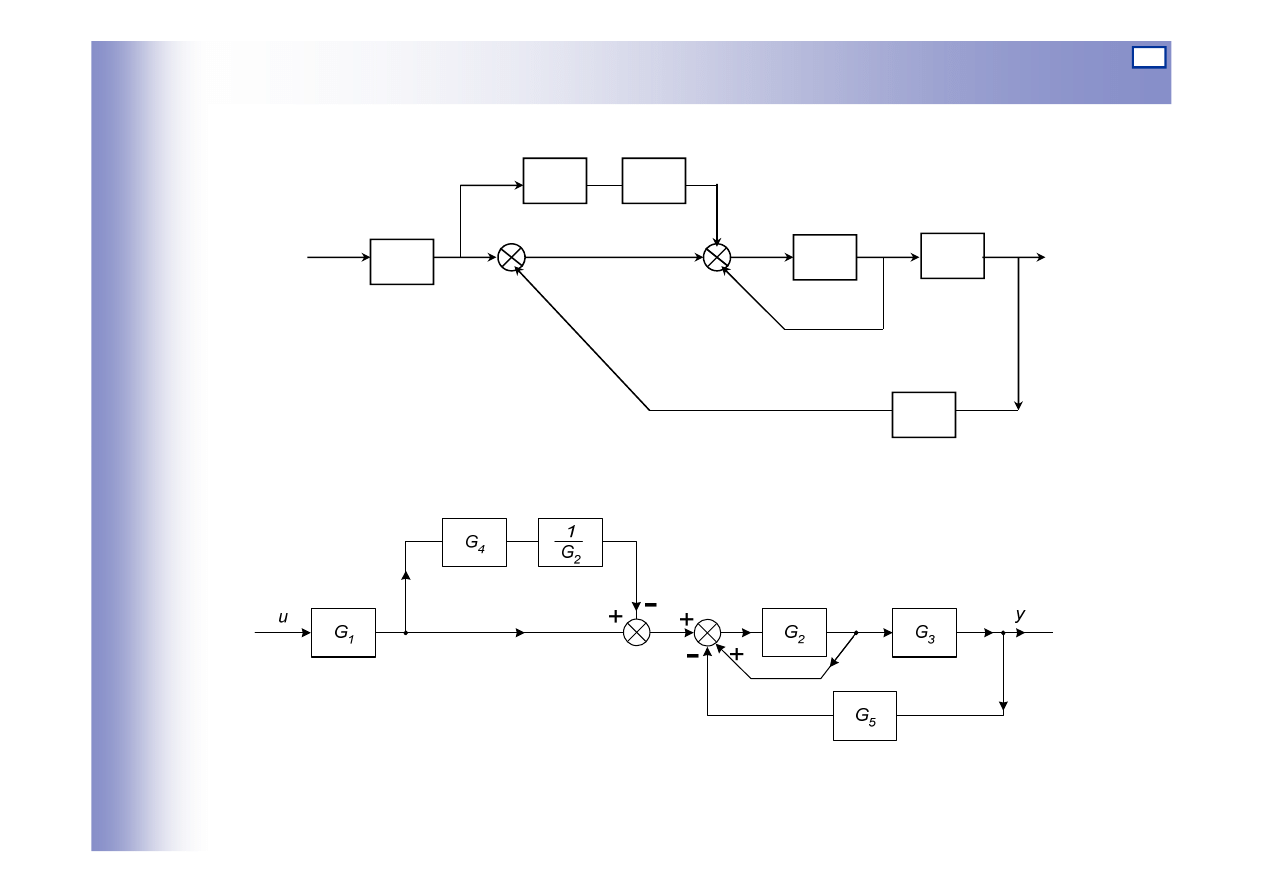
18
Przekształcenia schematów blokowych – przykład 2
G
1
G
2
G
3
G
4
G
5
1/G
2
-
+
+
+
-
c)
u
y
d)
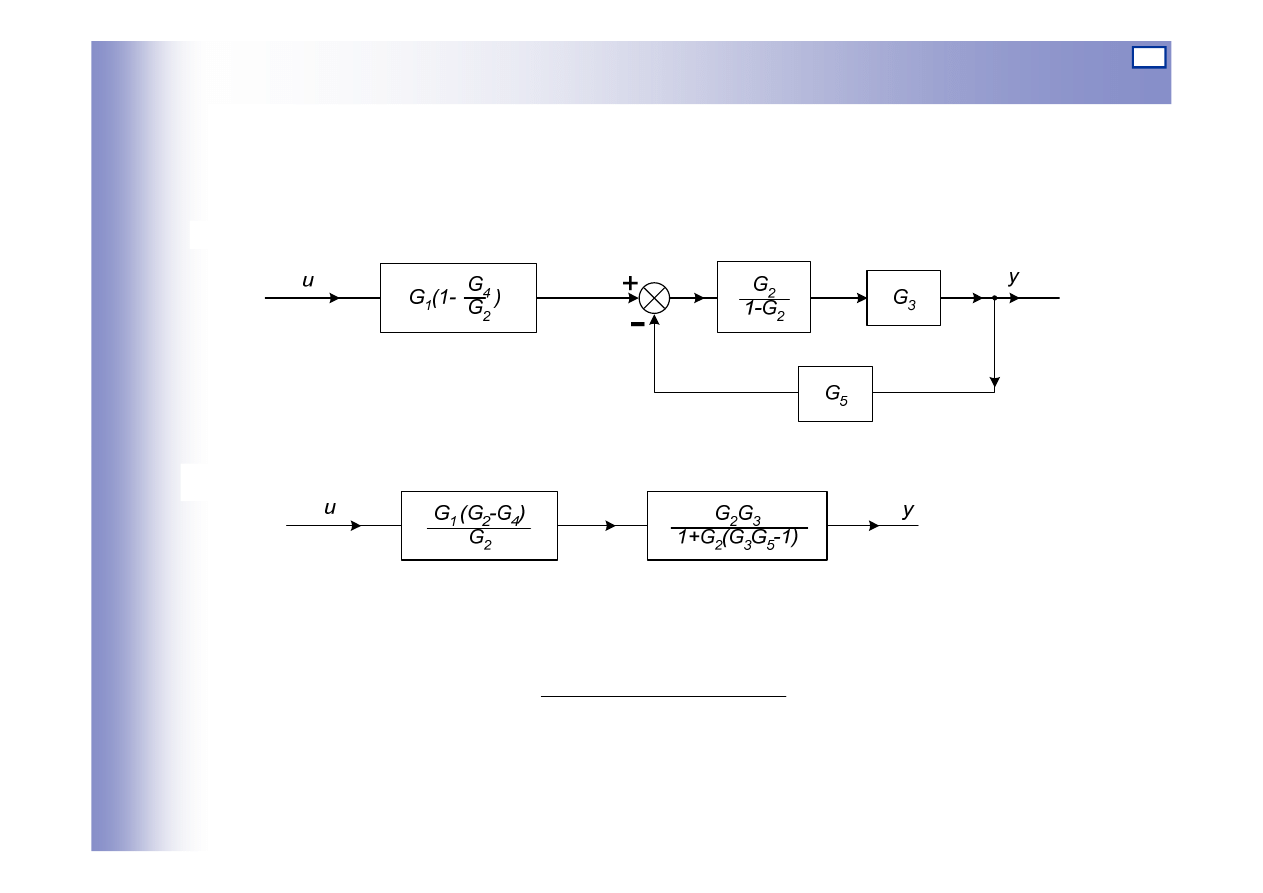
19
Przekształcenia schematów blokowych – przykład 2
e)
)
1
(
1
)
(
)
(
5
3
2
4
2
3
1
−
+
−
=
G
G
G
G
G
G
G
s
G
f)
20
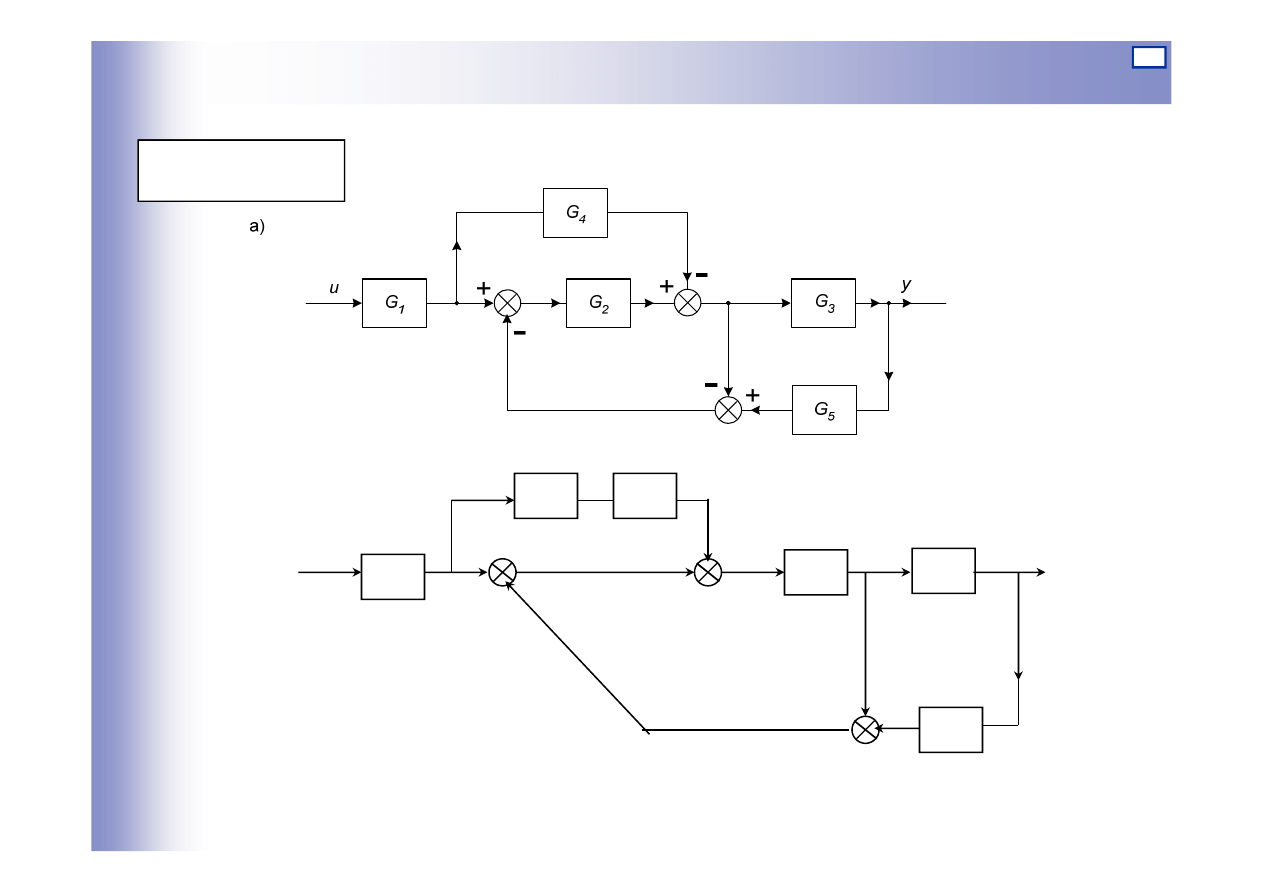
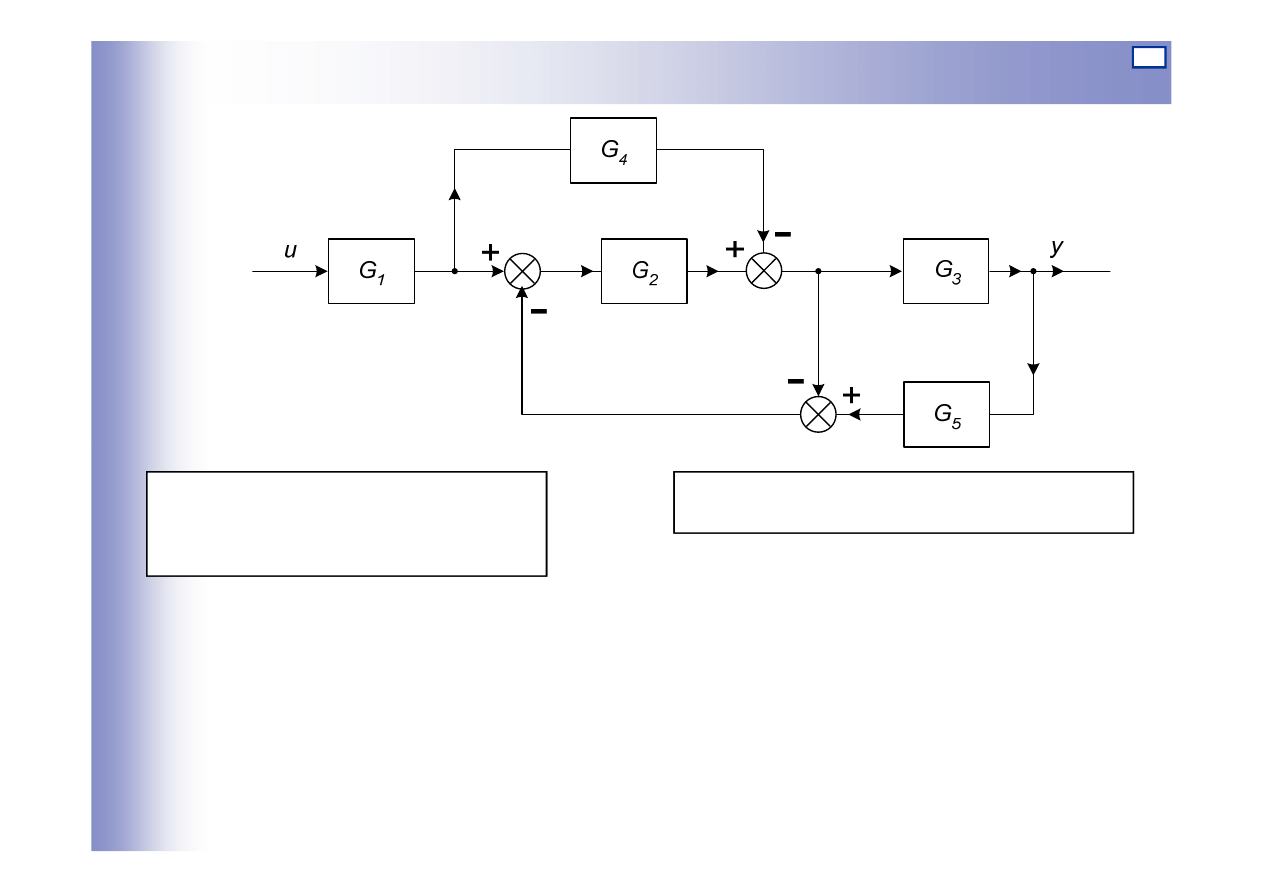
Przekształcenia schematów blokowych – przykład II
α
γ
χ
δ
ε
φ
γ
η
α
y
G
G
y
G
G
u
G
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
5
3
2
4
1
α
γ
ε
φ
δ
η
δ
γ
α
χ
η
φ
γ
χ
δ
ε
−
=
−
=
−
=
Równania węzłów sumacyjnych
:
Równania poszczególnych
bloków
:

21
Przekształcenia schematów blokowych – przykład 2
)
(
)
(
)
1
(
)
(
)
(
)
(
)
(
)
(
5
2
4
2
1
5
2
4
2
1
2
5
2
4
2
1
2
4
2
1
2
4
2
4
2
4
3
3
⋅
⋅
−
−
⋅
⋅
⋅
=
⋅
⋅
−
−
⋅
⋅
=
−
⋅
−
⋅
⋅
−
−
⋅
⋅
=
⋅
−
−
⋅
⋅
=
⋅
−
−
⋅
=
⋅
−
−
⋅
=
⋅
−
⋅
=
−
=
⋅
=
y
G
G
G
G
G
u
G
y
y
G
G
G
G
G
u
G
y
G
G
G
G
G
u
G
G
G
G
u
G
G
G
G
G
G
G
G
y
4
4
4
4
4
4
4
4
4
4
3
4
4
4
4
4
4
4
4
4
4
2
1
c
γ
γ
γ
χ
χ
δ
γ
δ
χ
δ
δ
ε
γ
η
φ
γ
γ
)
1
(
1
)
(
)
(
)
)
1
((
)
(
)
(
)
(
)
(
)
(
)
)
1
((
)
1
(
)
(
3
5
2
4
2
3
1
3
5
2
2
4
2
3
1
4
2
3
1
3
5
2
2
2
5
2
4
2
1
3
−
⋅
⋅
+
−
⋅
⋅
=
⋅
⋅
+
−
−
⋅
⋅
=
=
−
⋅
⋅
⋅
=
⋅
⋅
+
−
⋅
−
⋅
⋅
−
−
⋅
⋅
⋅
=
G
G
G
G
G
G
G
s
G
G
G
G
G
G
G
G
G
s
u
s
y
s
G
G
G
G
G
u
G
G
G
G
y
G
y
G
G
G
G
G
u
G
y
22
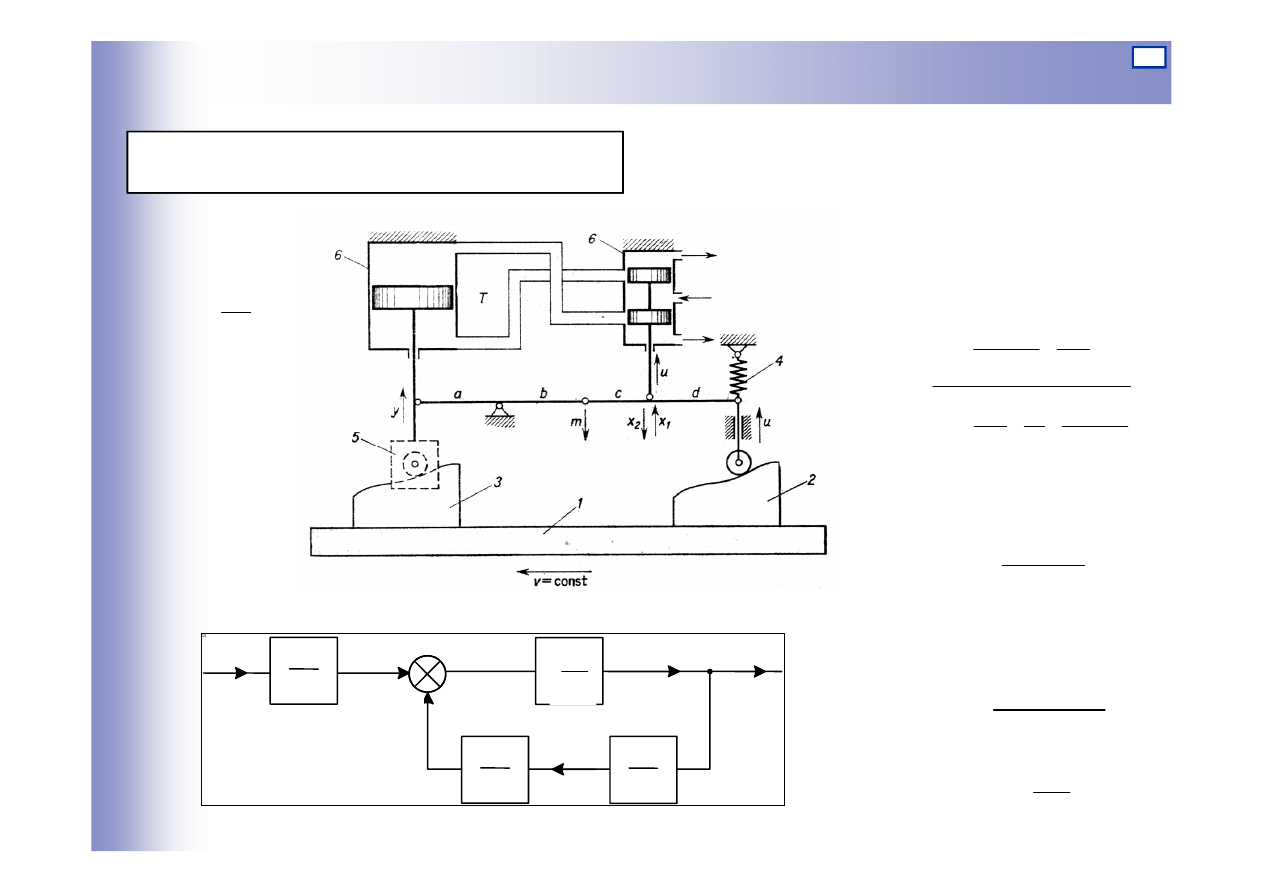
Przykład układania schematów blokowych
1
)
(
1
+
=
s
T
k
s
G
Schemat kopiału hydraulicznego:
Ts
s
G
1
)
(
1
=
d
c
d
a
b
Ts
Ts
d
c
c
s
G
+
⋅
⋅
+
⋅
+
=
1
1
1
)
(
bd
ac
k
=
bd
d
c
Ta
T
)
(
1
+
=
1
)
(
1
+
=
s
T
k
s
G
d
c
a
Ts
+
u
+
-
u
2
x
c
c+d
x
1
d
c+d
b
a
1
T
s
m
y
Nie można wy świetlić obrazu. Na k omputerze może brak ować pamięci do otwarcia obrazu lub obraz może by ć uszk odzony . Uruchom ponownie k omputer, a następnie otwórz plik ponownie. Jeśli czerwony znak x nadal będzie wy świetlany , k onieczne może by ć usunięcie obrazu, a następnie ponowne wstawienie go.
2
x
Ts
1
23
Przykład układania schematów blokowych
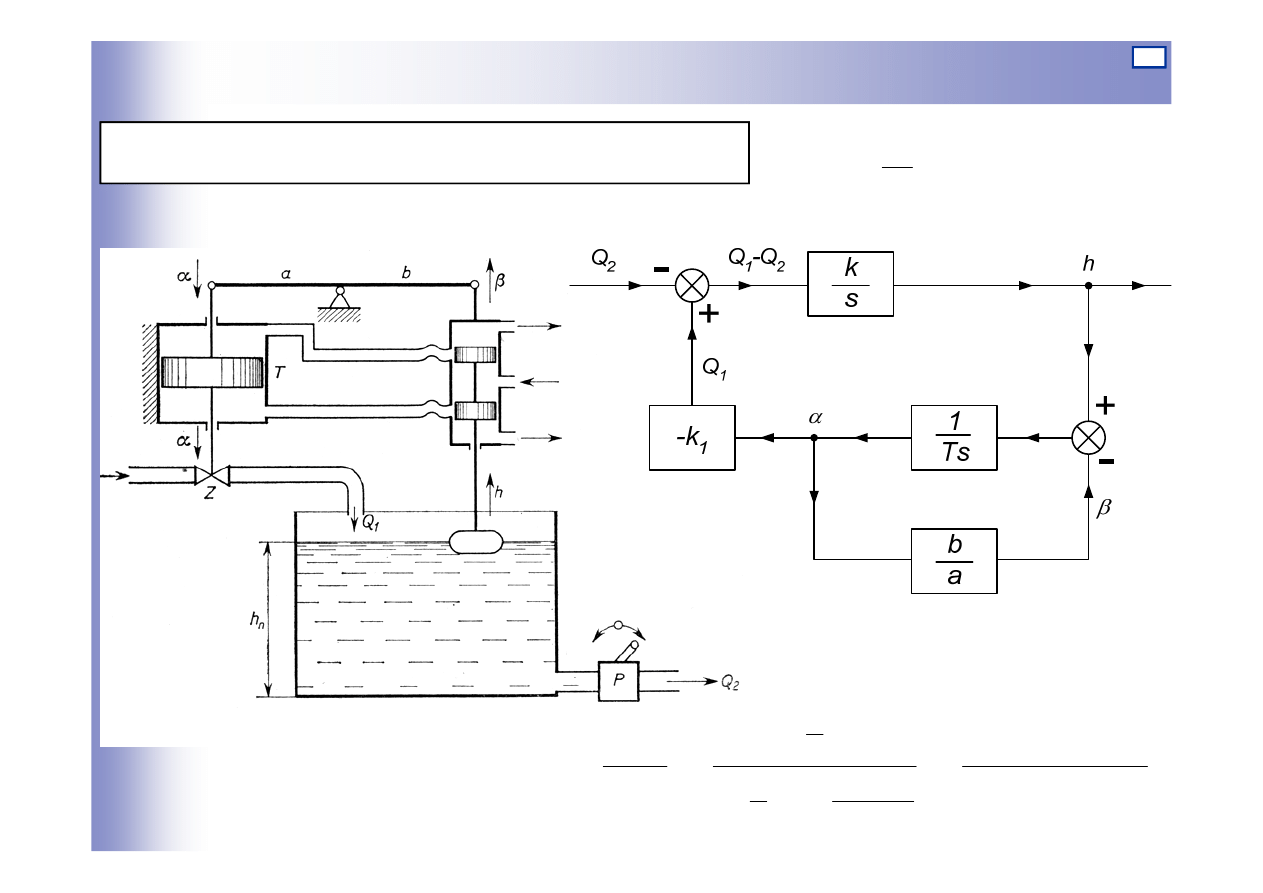
Układ regulacji poziomu cieczy w zbiorniku:
)
(
2
1
Q
Q
k
dt
dh
−
=
a
kk
b
aTs
s
b
aTs
k
b
aTs
a
k
s
k
s
k
s
Q
s
h
s
G
1
1
2
)
(
)
(
)
(
1
)
(
)
(
)
(
+
+
+
−
=
+
−
−
−
=
=
24
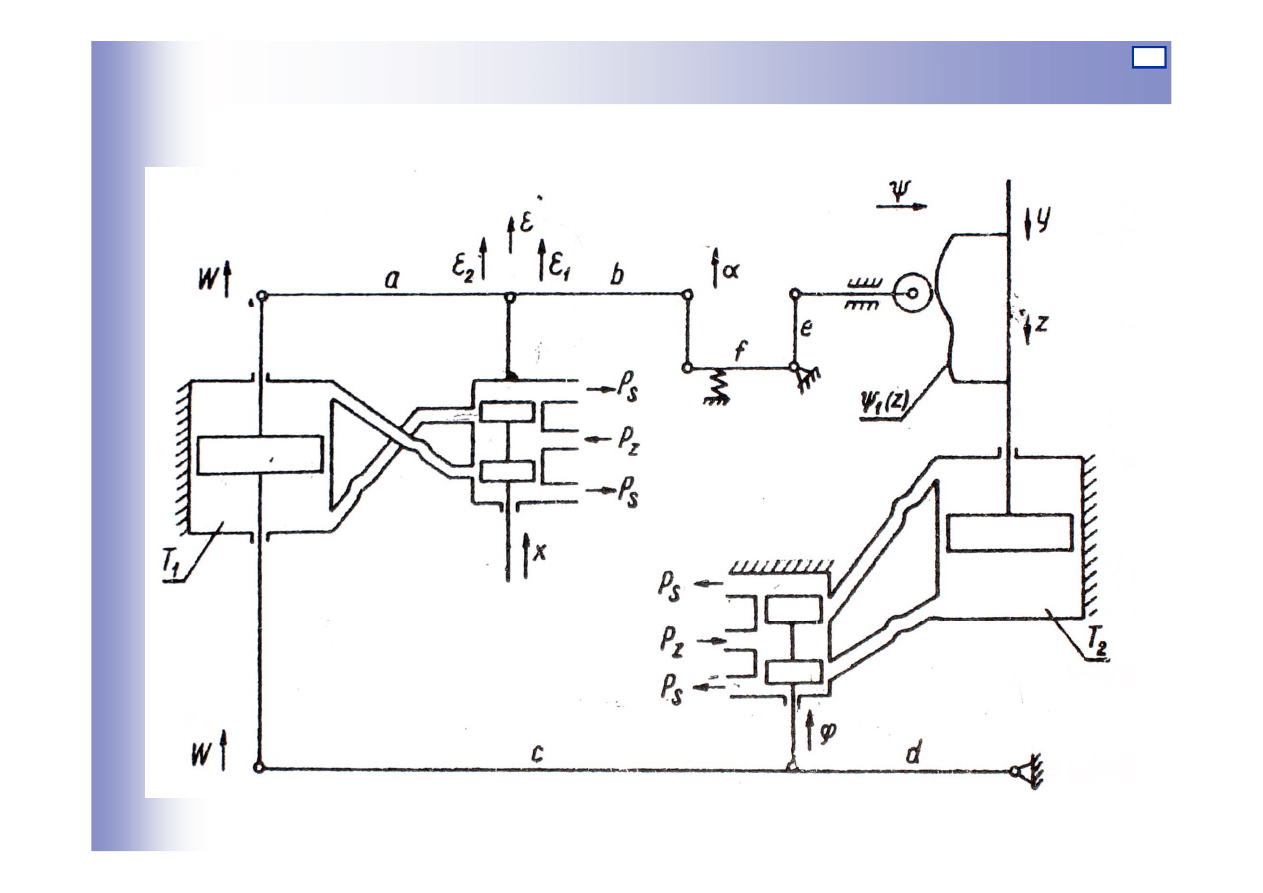
Przykład
25
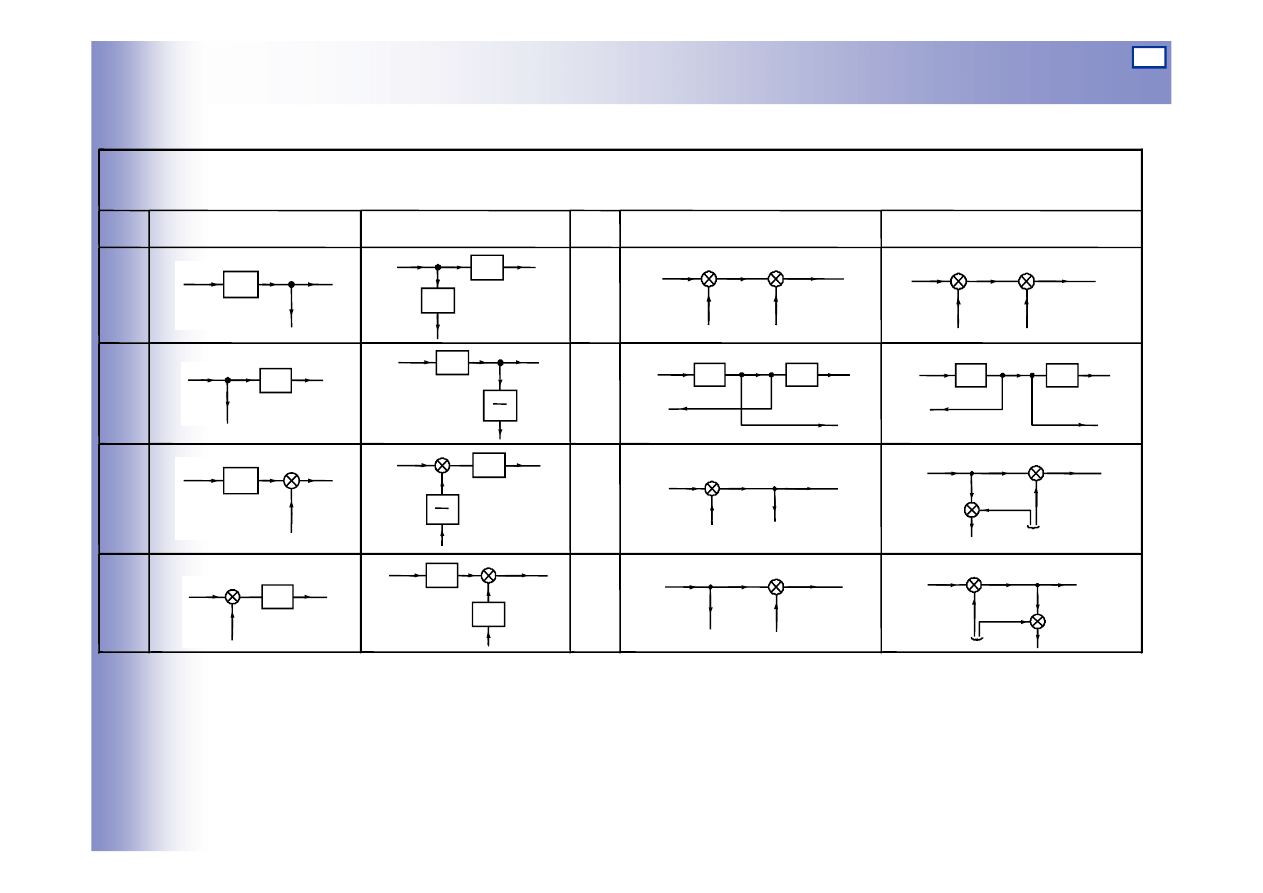
Przesunięcia węzłów informacyjnych i sumacyjnych
Przesunięcia węzłów informacyjnych i sumacyjnych
L.p.
Schemat pierwotny
Schemat równoważny
L.p.
Schemat pierwotny
Schemat równoważny
1
u
y
y
G
u
y
y
G
G
5
-
u
1
y
u
2
+
+
+
u
3
u
1
-u
2
y=u
1
-u
2
+u
3
-
u
1
y
u
2
+
+
+
u
3
u
1
+u
2
y=u
1
+u
2
-u
3
2
u
y
u
G
u
y
u
G
1
G
6
u
y
1
y
2
G
1
G
2
y
1
y
1
u
y
1
y
2
G
1
G
2
y
1
y
1
3
-
u
1
y
u
2
G
+
-
u
1
y
u
2
G
+
1
G
7
u
1
y
u
2
+
-
y
y=u
1
-u
2
u
1
y
+
-
u
2
y=u
1
-u
2
y
+
-
4
-
u
1
y
u
2
G
+
-
u
1
y
u
2
G
+
G
8
u
1
y
u
1
+
-
u
2
y=u
1
-u
2
y
u
1
+
-
u
2
u
1
+
+
y=u
1
-u
2
Wyszukiwarka
Podobne podstrony:
04 Schematy blokoweid 4893
04 schematy blokowe
04 tworzenie schematow blokowych
5 Algorytmy i schematy blokowe
3 Projektowanie układów automatyki (schematy blokowe, charakterystyki)
10 schematy blokowe i grafy (jako zobrazowanie modeli matematycznych)
Schemat blokowy For 1
Schemat blokowy Do While 2
SCHEMAT BLOKOWY
SCHEMAT BLOKOWY RADARU
Algebra schematów blokowych c d
Schemat blokowy If 1
Schemat blokowy For 3
SCHEMATY BLOKOWE ODBIORNIKÓW
06-10, schematy-blokowe
Schemat blokowy While 3
kl 2, folie1, ZAPIS PROGRAMU ZA POMOCĄ SCHEMATÓW BLOKOWYCH
Schematy , Schemat blokowy produkcji sadzonek So 1/0; 2/0
więcej podobnych podstron