Badanie stabilności numerycznej

Ćwiczenie to miało na celu porównaniu metod analitycznych z numerycznymi przy

rozwiązywania całki oznaczonej danej wzorem:

Gdzie: n – parametr naturalny z przedziału [1,8]

Za pomocą metod symbolicznych w programie matlab obliczyłem dokładne wartości

ośmiu całek:

>>%n=1
>> pretty(int(x/(x + 5),x,0,1))

/ 6 \
1 - 5 log| - |
\ 5 /

>>%n=2
>> pretty(int(x^2/(x + 5),x,0,1))

9
25 log(6) - 25 log(5) - -
2

>>%n=3
>> pretty(int(x^3/(x + 5),x,0,1))

/ 5 \ 137
125 log| - | + ---
\ 6 / 6

>>%n=4
>> pretty(int(x^4/(x + 5),x,0,1))

/ 5 \ 1367
- 625 log| - | - ----
\ 6 / 12

>>%n=5
>> pretty(int(x^5/(x + 5),x,0,1))

/ 5 \ 34187
3125 log| - | + -----
\ 6 / 60

>>%n=6
>> pretty(int(x^6/(x + 5),x,0,1))

/ 5 \ 11395
- 15625 log| - | - -----
\ 6 / 4

>>%n=7
>> pretty(int(x^7/(x + 5),x,0,1))

/ 5 \ 398829
78125 log| - | + ------
\ 6 / 28

>>%n=8
>> pretty(int(x^8/(x + 5),x,0,1))

/ 5 \ 3988283
- 390625 log| - | - -------
\ 6 / 56

W tabeli 1.2 są umieszczone wartości całek w zależności od parametru n, tabela zawiera
również wartości wyliczone za pomocą m-pliku

1.Błąd! W dokumencie nie ma tekstu o podanym stylu..1 - Wyniki

Parametr n:

n=1

n=2

n=3

n=4

n=5

n=6

n=7

n=8

Wartość

całki:

0.0884

0.0580

0.0431

0.0343

0.0285

0.0243

0.0212

0.0188

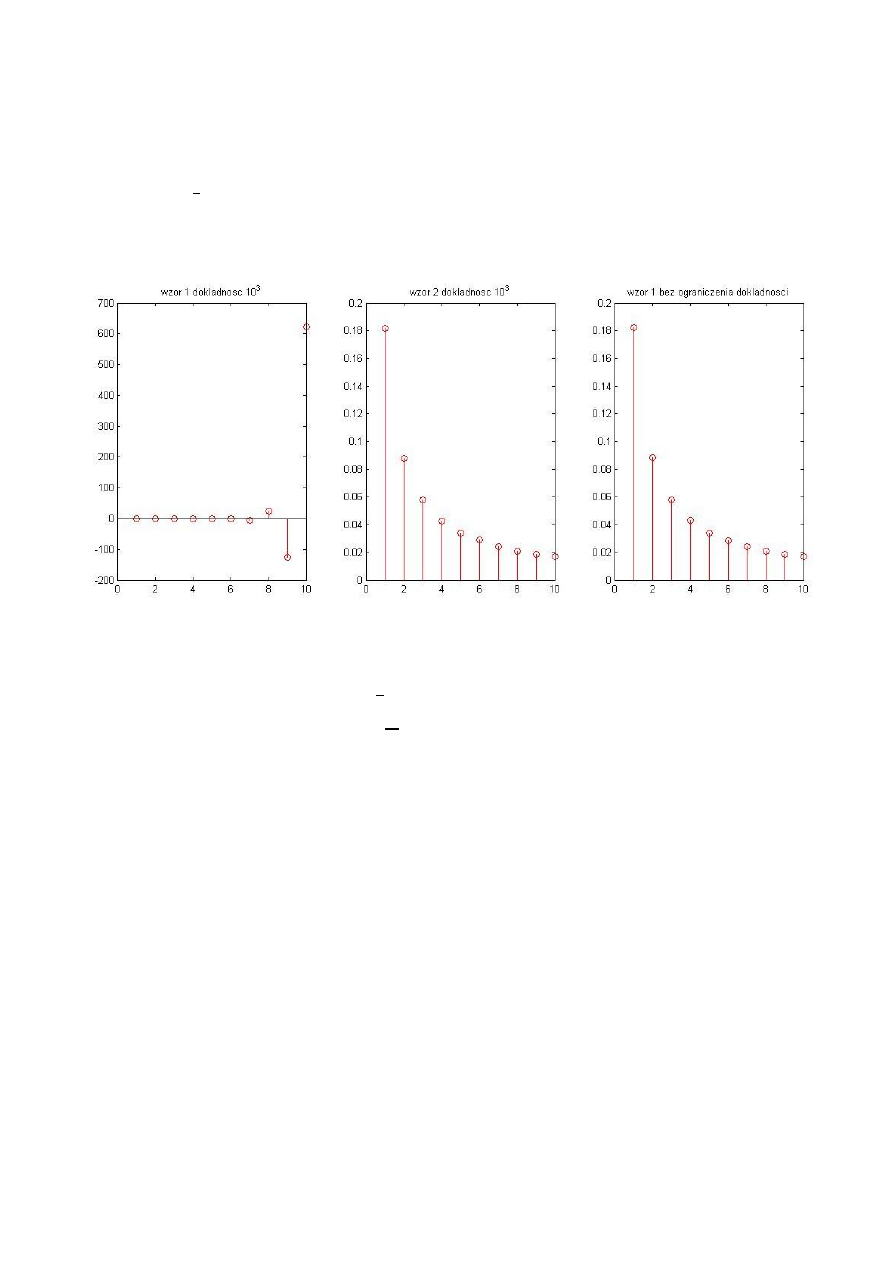
Za pomocą m-pliku otrzymałem diagramy słupkowe(wykresy 1.3) przedstawiające

wartości obliczonych całek, m-plik został przeze mnie zmodyfikowany tak by dla każdej z
metod liczyć przypadki dla n od 1 do 8, należy pamiętać że pierwszy słupek przedstawia

wartość

, kolejne przedstawiają już odpowiednie wartości w zależności od parametru n:

Wartości całek w przypadku pierwszego wzoru liczone były rekurencyjnie zaczynając

od wartości dla n=1 czyli:

. Wzór drugi liczył rekurencyjnie w dół zaczynając od

uproszczonej wartości dla n=8, czyli:

. Łatwo zauważyć, że ograniczenie dokładności do 3

cyfr znaczących nie wpłynęło znacznie na poprawność wyników (odnosząc się do „wzór 1
bez ograniczeń” gdzie wartości są liczone z dużą precyzją) w przypadku wzoru nr.2,
natomiast dla pierwszego wzoru wyniki są przekłamane prawie sześciokrotnie. Jest to
spowodowane propagacją błędu zaokrąglenia jaki pojawia się na początku procedury
rekurencyjnej. Ta niedokładność wraz z każdym krokiem staje się coraz większa, w ósmym
kroku wynik różni się o cztery rzędy wielkości! Niemożna jednak powiedzieć, że algorytm
jest niestabilny ponieważ istnieje taka dokładność dla której wyniki są bliskie wzorcowym.
Przy dziewięciu cyfrach znaczących nie widać już różnicy w wynikach otrzymanych za
pomocą wzoru nr.1 i nr.2 (wykresy 1.4)

1.Błąd! W dokumencie nie ma tekstu o podanym stylu..2 - Wyniki dla dokładności 10^3

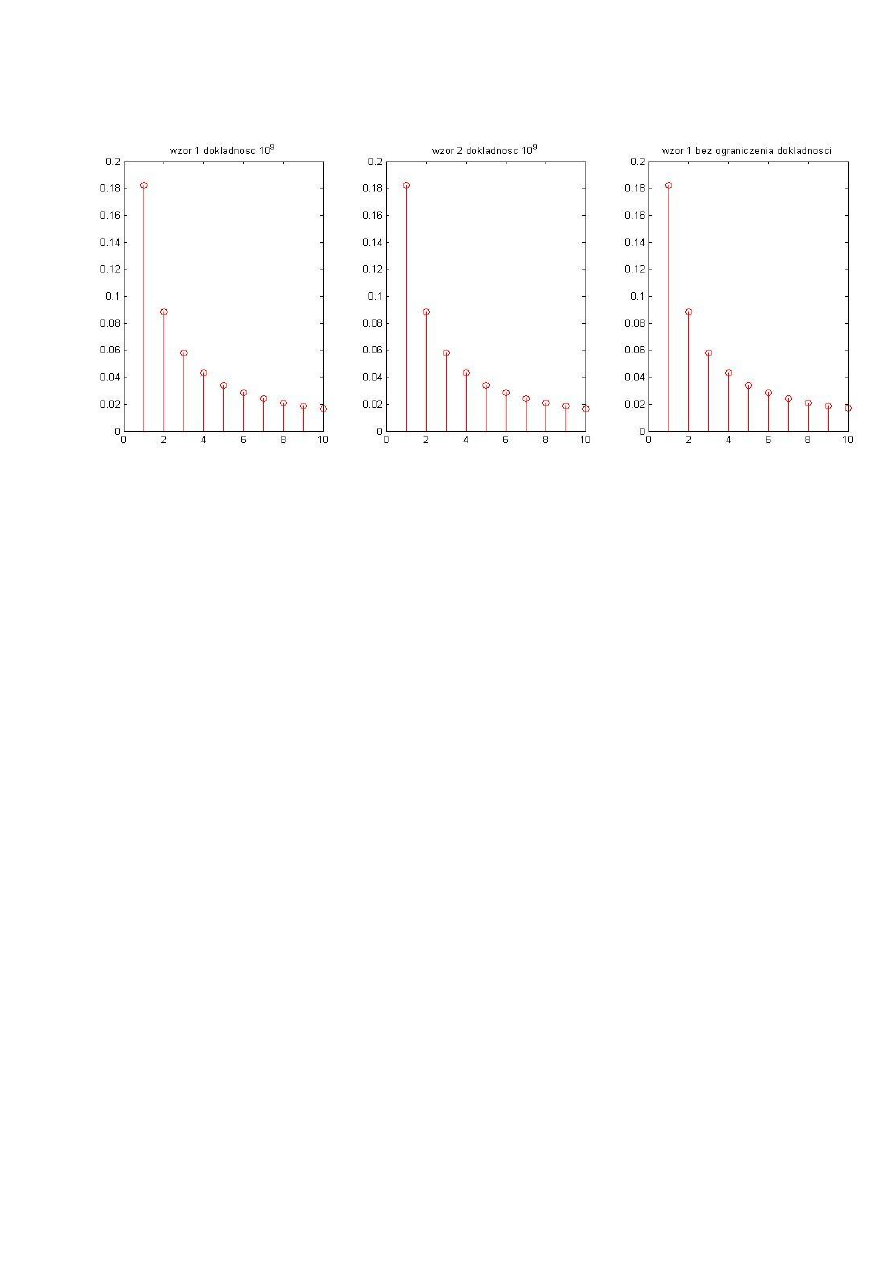
1.3 - Wykresy dla dokładności 10^9