Z. Kąkol-Notatki do Wykładu z Fizyki
Wykład 21
21. Prąd elektryczny i pole magnetyczne
21.1 Prąd elektryczny
Natężenie prądu elektrycznego
t
Q
I
=
(21.1)
Jednostka: 1 amper, 1A.
Gęstość prądu elektrycznego
S
I
j
= (21.2)
W nieobecności zewnętrznego pola elektrycznego elektrony poruszają się chaotycz-
nie we wszystkich kierunkach. W zewnętrznym polu E uzyskują wypadkową (stałą z
założenia)
prędkość unoszenia
v
u
.
Jeżeli n jest koncentracją elektronów to ilość ładunku Q jaka przepływa przez przewod-
nik o długości l w czasie t = l/v
u
wynosi
Q = nSle
l
S
Tak więc natężenie prądu wynosi
u
u
nSe
l
nSle
t
Q
I
v
v
=
=
=
(21.3)
a gęstość prądu
u
u
ne
S
I
j
v
v
ρ
=
=
=
(21.4)
gdzie
ρ jest gęstością ładunku.
UMOWA: kierunek prądu = kierunek ruchu ładunków dodatnich.
21-1

Z. Kąkol-Notatki do Wykładu z Fizyki
Przykład 1
Prąd o natężeniu 1A płynie w drucie miedzianym o przekroju 1 mm
2
. Jaka jest średnia
prędkość unoszenia elektronów przewodnictwa ? Masa atomowa miedzi
µ = 63.8
g/mol, a gęstość
ρ = 8.9 g/cm
3
.
Z równania na natężenie prądu otrzymujemy
nSe
I
u
=
v
Zakładamy, że na jeden atom przypada 1 elektron przewodnictwa (Cu
+1
). Możemy więc
obliczyć koncentrację nośników
µ
ρ
Av
N
n
=
n = 8.4·10
28
atom/m
3
Wstawiając do równania na prędkość otrzymujemy
v
u
= 7.4·10
-5
m/s = 0.074 mm/s
Prądy mogą też płynąć w gazach i cieczach. Lampy jarzeniowe są przykładem wyko-
rzystania przepływu prądu w gazach. W gazach prąd jest wynikiem ruchu nie tylko
elektronów ale i jonów dodatnich. Jednak lżejsze elektrony są znacznie szybsze i ich
wkład do prądu jest dominujący. W zderzeniu elektronu z jonem lub atomem gazu
energia może zostać zaabsorbowana przez atom, a następnie wypromieniowana w po-
staci promieniowania elektromagnetycznego w tym również widzialnego.
21.2 Prawo Ohma
Jeżeli do przewodnika przyłożymy różnicę potencjałów V, to przez przewodnik płynie
prąd I. Na początku XIX wieku Ohm zdefiniował
opór przewodnika
jako napięcie po-
dzielone przez natężenie prądu
I
U
I
V
R
=
∆
=
(21.5)
Jest to definicja oporu. Ten stosunek jest stały pod warunkiem, że utrzymuje się stałą
temperaturę.
Jednostką oporu (SI) jest 1 (Ohm) 1
Ω.
21.2.1 Wyprowadzenie prawa Ohma
Bez pola elektrycznego prędkość ruchu chaotycznego u (nie powoduje przepływu
prądu). Prędkość u jest związana ze średnią drogą swobodną
λ i średnim czasem po-
między zderzeniami
∆t zależnością: u =
λ/∆t.
21-2

Z. Kąkol-Notatki do Wykładu z Fizyki
Jeżeli przyłożymy napięcie to na każdy elektron będzie działała siła F = eE i po czasie
∆t każdy elektron osiągnie prędkość unoszenia v
u
=
∆u daną II zasadą Newtona
eE
t
u
m
=
∆
∆
Stąd
m
t
eE
u
u
∆
=
=
∆
v
Podstawiając
∆t =
λ/u otrzymujemy
mu
E
e
u
λ
=
v
(21.6)
Prędkość unoszenia ma ten sam kierunek (przeciwny do E) dla wszystkich elektronów.
Przy każdym zderzeniu elektron traci prędkość unoszenia.
Średnia droga swobodna
λ jest tak mała, że v
u
jest zawsze mniejsza od u.
Obliczamy teraz natężenie prądu wstawiając wyrażenie na v
u
do wyrażenia (21.3) na
natężenie I.
mu
SE
ne
nSe
I
u
λ
2
=
=
v
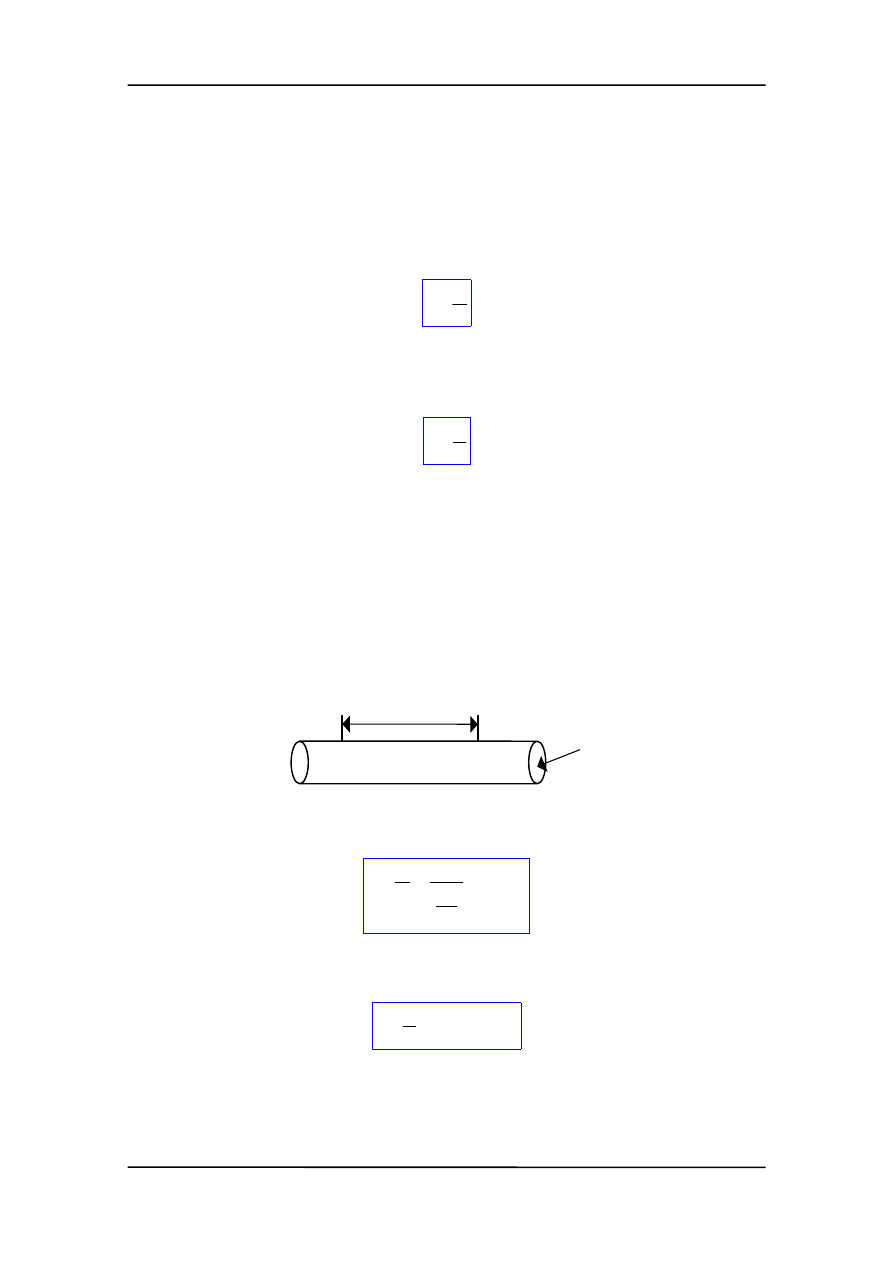
Dla elementu przewodnika o długości l (rysunek) obliczymy opór korzystając z faktu,
że napięcie U = El.
Z prawa Ohma
S
ne
mul
I
El
I
U
R
λ
2
=
=
=
(21.7)
R jest proporcjonalny do długości przewodnika i odwrotnie proporcjonalny do przekro-
ju. Zauważmy, że R pozostaje stały tak długo jak długo u jest stałe, a u zależy tylko od
temperatury (patrz wykład 15).
Równanie (21.7) przepiszmy w postaci
S
l
R
ρ
=
(21.8)
Stałą
ρ nazywamy
oporem właściwym
.
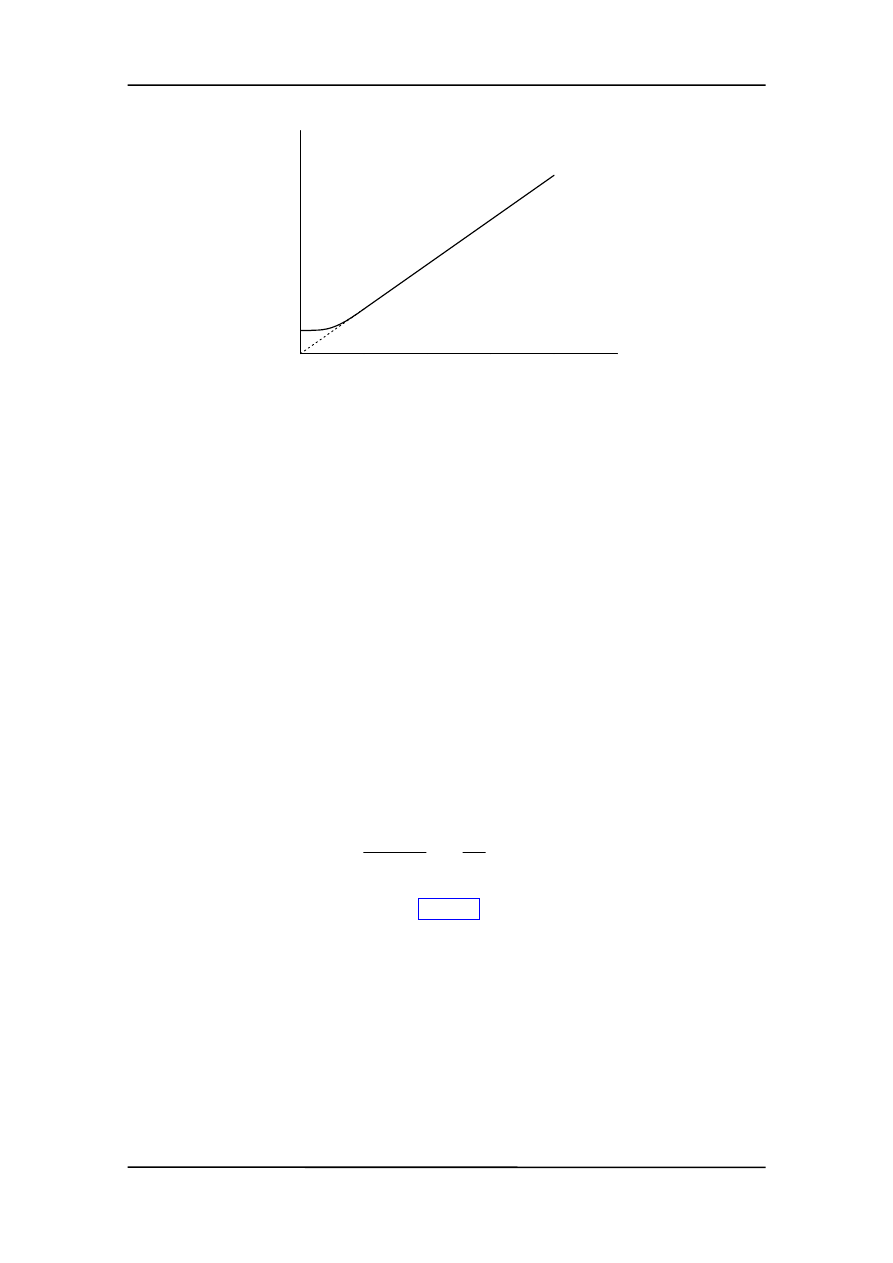
Typowa zależność oporu od temperatury dla przewodników metalicznych jest poka-
zana na rysunku na następnej stronie.
Z dobrym przybliżeniem jest to zależność liniowa
ρ ~ T za wyjątkiem temperatur bli-
skich zera bezwzględnego. Wtedy zaczyna odgrywać rolę tzw. opór resztkowy
ρ
0
za-
leżny w dużym stopniu od czystości metalu. Istnieją jednak metale i stopy, dla których
obserwujemy w dostatecznie niskich temperaturach całkowity zanik oporu. Zjawisko to
nosi nazwę
nadprzewodnictwa
.
21-3
Z. Kąkol-Notatki do Wykładu z Fizyki
ρ
0
0
T
ρ
Prądy wzbudzone w stanie nadprzewodzącym utrzymują się w obwodzie bez zasilania
zewnętrznego. Ta możliwość utrzymania stale płynącego prądu rokuje duże nadzieje na
zastosowania techniczne, które znacznie wzrosły po odkryciu w 1987 r materiałów
przechodzących w stan nadprzewodzący w stosunkowo wysokich temperaturach, około
100 K. Materiały te noszą nazwę wysokotemperaturowych nadprzewodników a ich od-
krywcy Bednorz i Müller zostali wyróżnieni Nagrodą Nobla.
21.3 Straty cieplne
Gdy elektron zderza się z atomem traci nadwyżkę energii, którą uzyskał w polu
elektrycznym. Ponieważ energia kinetyczna nie wzrasta, cała energia stracona przez
elektrony daje
dE
cieplna
= Udq
gdzie dq jest ładunkiem przepływającym(elektronów przewodnictwa).
Dzieląc obie strony przez dt otrzymujemy
UI
t
q
U
t
E
a
ciep
=
=
d
d
d
d
ln
P = UI
(21.8)
przedstawia
straty mocy elektrycznej
.
21.3.1 Siła elektromotoryczna
Aby utrzymać prąd potrzeba źródła energii elektrycznej. Np. baterie, generatory.
Nazywamy je źródłami
siły elektromotorycznej SEM
. W takich źródłach jeden rodzaj
energii jest zamieniany na drugi. SEM oznaczamy
ε i definiujemy
21-4
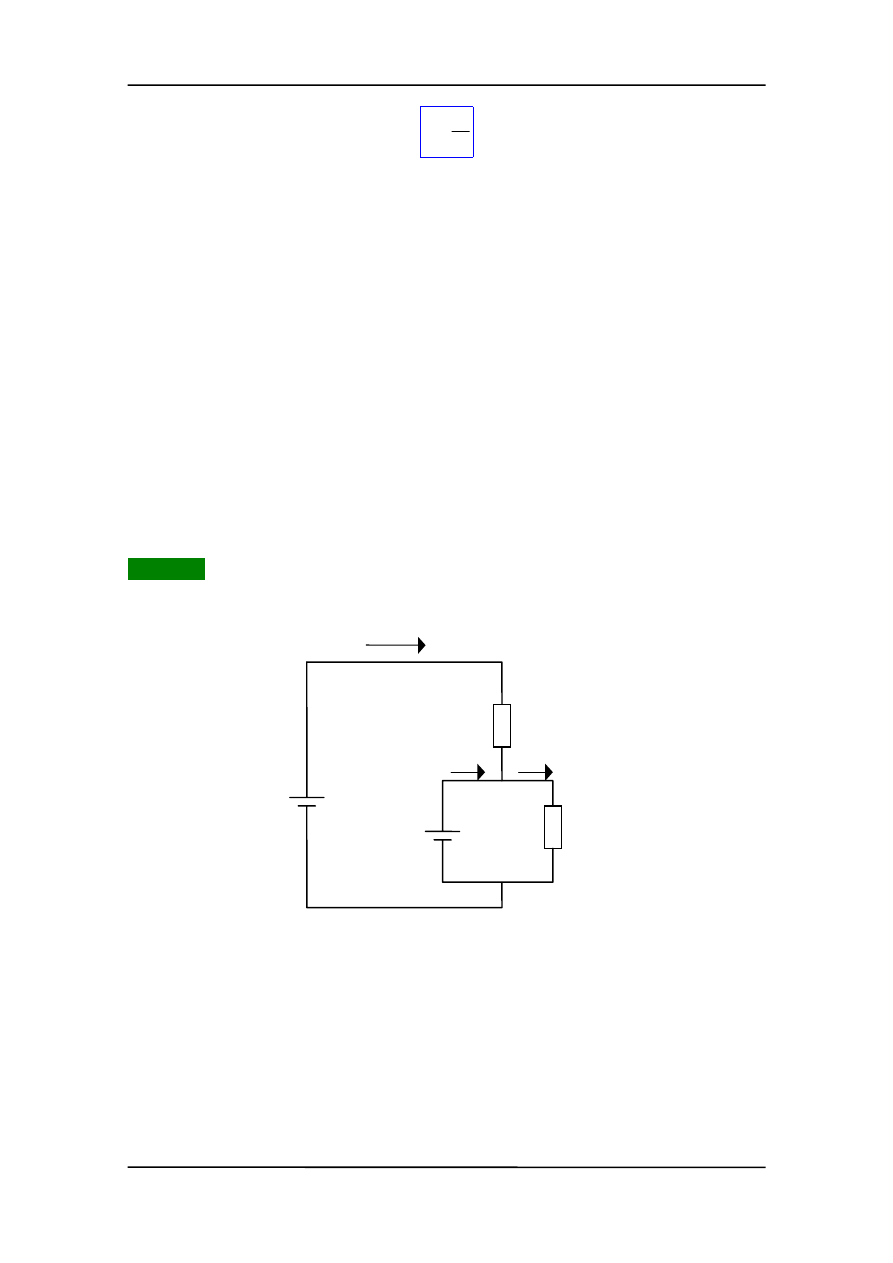
Z. Kąkol-Notatki do Wykładu z Fizyki
q
W
=
ε
(21.9)
gdzie W jest energią elektryczną przekazywaną ładunkowi q, gdy przechodzi on przez
źródło SEM.
21.4 Obwody prądu stałego
Łączenie oporów:
• szeregowe (ten sam prąd przez oporniki) R
z
= R
1
+ R
2
+ .....
• równoległe (to samo napięcie na opornikach) 1/R
z
= 1/R
1
+ 1/R
2
+ .....
21.4.1 Prawa Kirchoffa
• Twierdzenie o obwodzie zamkniętym:
algebraiczna suma przyrostów napięć w do-
wolnym obwodzie zamkniętym jest równa zeru
. (Spadek napięcia jest przyrostem
ujemnym napięcia).
• Twierdzenie o punkcie rozgałęzienia:
algebraiczna suma natężeń prądów przepły-
wających przez punkt rozgałęzienia jest równa zeru
.
Twierdzenie o obwodzie zamkniętym jest wynikiem prawa zachowania energii, a twier-
dzenie o punkcie rozgałęzienia wynika z prawa zachowania ładunku.
Przykład 2
Regulator napięcia (rysunek).
I
2
R
2
ε
2
ε
1
R
1
I
1
I
3
Opornik R
1
ma napięcie określone przez
ε
1
a prąd pobiera z
ε
2
.
W każdej gałęzi obwodu trzeba z osobna przyjąć kierunek prądu i jego natężenie.
Prawdziwy kierunek rozpoznamy po znaku obliczonego natężenia. Spadek napięcia po-
jawia się przy przejściu przez każdy opornik w kierunku zgodnym z prądem. Przyrost
napięcia pojawia się przy przejściu przez źródło od "
−" do "+".
Zastosowanie I prawa Kirhoffa do "dużej" pętli daje
ε
2
– I
2
R
2
– I
3
R
1
= 0
21-5
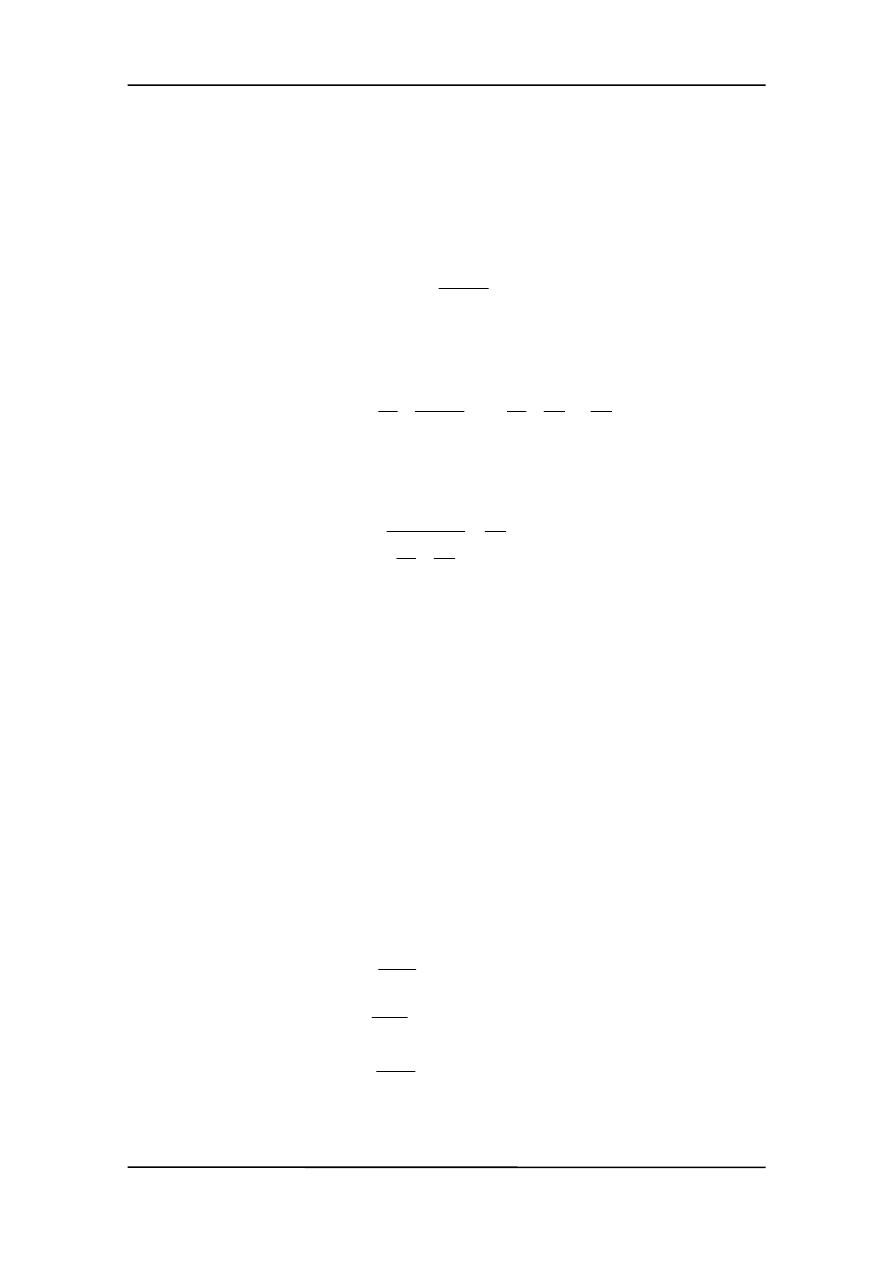
Z. Kąkol-Notatki do Wykładu z Fizyki
a dla "małej" pętli
ε
1
– I
3
R
1
= 0
Po odjęciu stronami otrzymamy
ε
2
–
ε
1
– I
2
R
2
= 0
2
1
2
2
R
I
ε
ε −
=
Dla węzła
I
1
+ I
2
– I
3
= 0
skąd
2
2
2
1
1
2
1
2
1
1
2
3
1
1
1
R
R
R
R
R
I
I
I
ε
ε
ε
ε
ε
−
+
=
−
−
=
−
=
Zauważmy, że gdy dobrać warunki tak aby
2
2
2
1
1
1
1
R
R
R
ε
ε
=
+
to I
1
= 0 i
ε
1
nie daje żadnego prądu. Taki układ ma ważne zastosowanie praktyczne.
Napięcie
1
ε może być niskoprądowym ogniwem wzorcowym, mimo że R
1
może pobie-
rać duży prąd (głównie z
ε
2
).
21.5 Pole magnetyczne
Doświadczalnie stwierdzamy, że występuje oddziaływanie:
• magnesów naturalnych (Fe
3
O
4
)
• oddziaływanie przewodników z prądem na ładunki w ruchu (kineskop)
• oddziaływanie przewodników z prądem na siebie
• magnesem jest sama Ziemia. Jej działanie na igłę kompasu jest znane od Starożytno-
ści.
Te oddziaływania opisujemy wprowadzając pojęcie
pola magnetycznego
.
21.5.1 Siła magnetyczna
Pole grawitacyjne (natężenie)
m
F
g
graw
=
Pole elektryczne (natężenie)
q
F
E
elekt
=
Pole magnetyczne (indukcja)
v
q
F
B
magn
=
(Siła działa na ładunki w ruchu i jest proporcjonalna do q
v
).
Jednostką B jest tesla; 1T = N/(Am)
21-6

Z. Kąkol-Notatki do Wykładu z Fizyki
Powyższy wzór jest prawdziwy dla ruchu ładunku prostopadle do B ale siła F
magn
(
siła Lorentza
) zależy od kierunku v. Ta zależność od kierunku jest zapisana poprzez
równanie wektorowe
B
F
×
= v
q
magn
(21.10)
gdzie kierunek definiuje się z reguły śruby prawoskrętnej (iloczyn wektorowy).
Zauważmy, że
F
magn
jest zawsze prostopadłe do v
. Zatem, zgodnie z twierdzeniem
o pracy i energii F
magn
nie może zmienić energii kinetycznej poruszającego się ładunku
i ładunek krąży po okręgu. Stąd
B
q
R
m
v
v =
2
qB
m
R
v
=
jest promieniem okręgu.
Siła działa na ładunki w ruchu więc działa na cały przewodnik z prądem.
F = e
v
u
B
B
nSe
I
e
F
=
W przewodniku o długości l znajduje się nSl elektronów, więc całkowita siła
lB
I
B
nS
I
l
nS
F
=
=
Równanie w ogólnym przypadku ma postać
B
l
F
×
= I
(21.11)
21.5.2 Działanie pola magnetycznego na obwód z prądem
Rozważymy teraz działanie pola magnetycznego na zamknięty obwód z prądem.
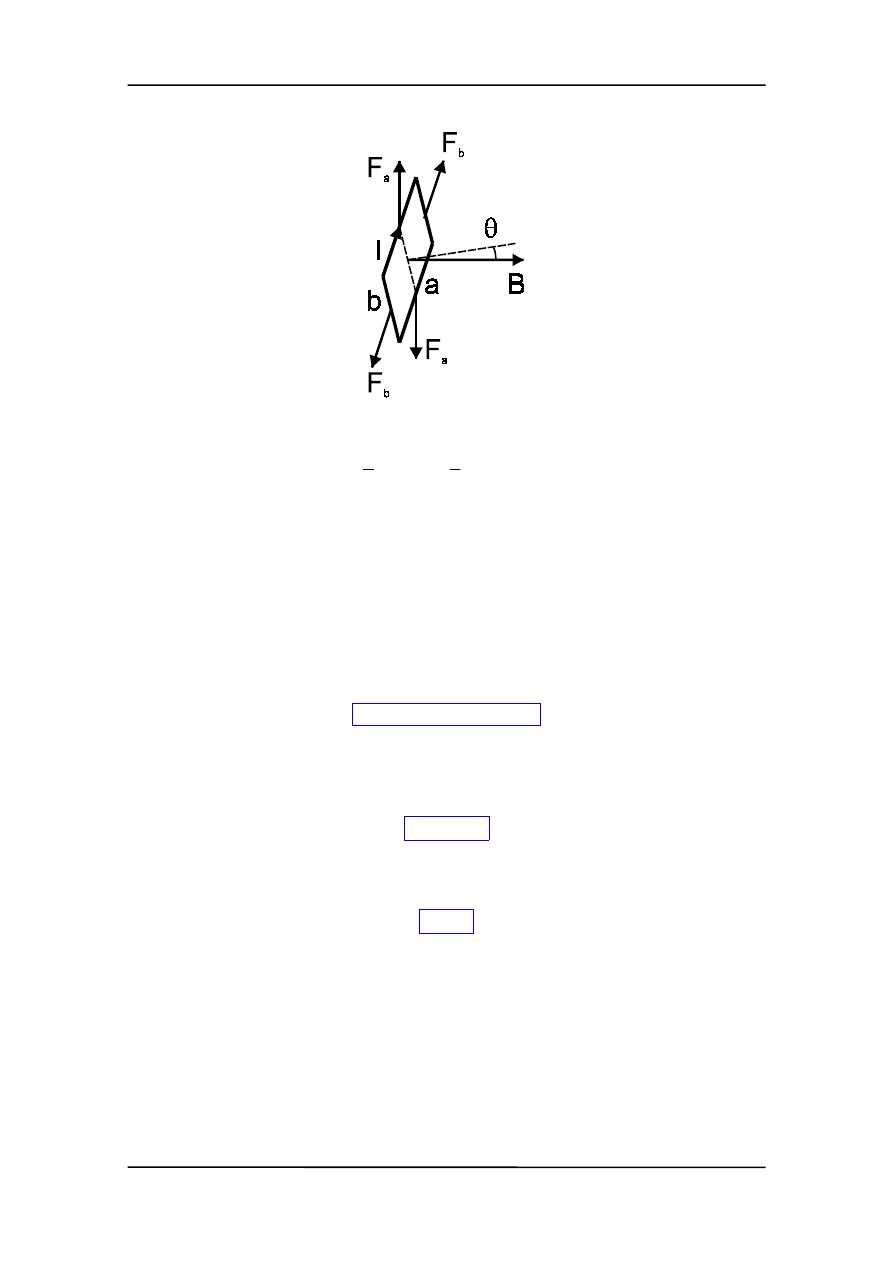
Prostokątną ramkę o bokach a i b umieszczamy w jednorodnym polu magnetycznym
o indukcji B. Przez ramkę płynie prąd o natężeniu I, a normalna do płaszczyzny ramki
tworzy kąt
θ z polem B (rysunek).
Rozpatrujemy siłę działającą na każdy z boków. Siły F
b
działające na odcinki b zno-
szą się wzajemnie. Siły F
a
działające na odcinki a też się znoszą ale tworzą parę sił da-
jącą wypadkowy moment siły
21-7
Z. Kąkol-Notatki do Wykładu z Fizyki
θ
θ
θ
τ
sin
sin
sin
b
F
b
F
b
F
a
a
a
=
+
=
2
2
lub wektorowo (na podstawie definicji iloczynu wektorowego)
b
F
ô
×
=
a
Siła F
a
wynosi
IaB
F
a
=
więc
θ
θ
τ
sin
sin
ISB
IabB
=
=
(21.12)
gdzie S = ab jest powierzchnią ramki. Równanie (21.12) możemy zapisać w postaci
wektorowej
B
S
τ
×
= I
(21.13)
gdzie S jest wektorem powierzchni.
Wielkość
S
ì
I
=
(21.14)
nazywamy
magnetycznym momentem dipolowym
. Pole magnetyczne działa więc na
ramkę z prądem (dipol magnetyczny) momentem skręcającym obracając ją. Położenie
równowagi ramki (dipola magnetycznego) występuje dla
θ = 0 tj. gdy ramka jest usta-
wiona prostopadle do pola B. Przykładem dipola magnetycznego jest igła kompasu, któ-
ra umieszczona w polu magnetycznym obraca się ustawiając zgodnie z polem.
Taką "kołową ramką z prądem" jest również elektron krążący po orbicie w atomie.
Moment dipolowy elektronu krążącego po orbicie o promieniu r wynosi
21-8
Z. Kąkol-Notatki do Wykładu z Fizyki
)
(
2
r
I
e
π
µ =
Natężenie prądu wytwarzanego przez elektron o ładunku e przebiegający orbitę w cza-
sie T (okres obiegu) wynosi
r
e
T
e
t
q
I
π
2
v
=
=
=
gdzie
v jest prędkością elektronu. Stąd
L
m
e
r
m
m
e
r
e
r
r
e
e
2
)
(
2
2
)
(
2
2
=
=
=
=
v
v
v π
π
µ
gdzie L = m
v
r jest momentem pędu elektronu. Elektron, krążący po orbicie jest więc
elementarnym dipolem magnetycznym. Własności magnetyczne ciał są właśnie okre-
ślone przez zachowanie się tych elementarnych dipoli w polu magnetycznym. Własno-
ści te omówimy na dalszych wykładach.
Z momentem siły działającym na dipol związana jest tzw.
energia magnetyczna
di-
pola Można również pokazać, że ta energia wyraża się wzorem
E
m
= -
µB = - µBcosθ
(21.15)
Zauważmy, że minimum energii odpowiada ustawieniu dipola w kierunku równoległym
do pola magnetycznego B (
θ = 0).
21.5.3 Efekt Halla
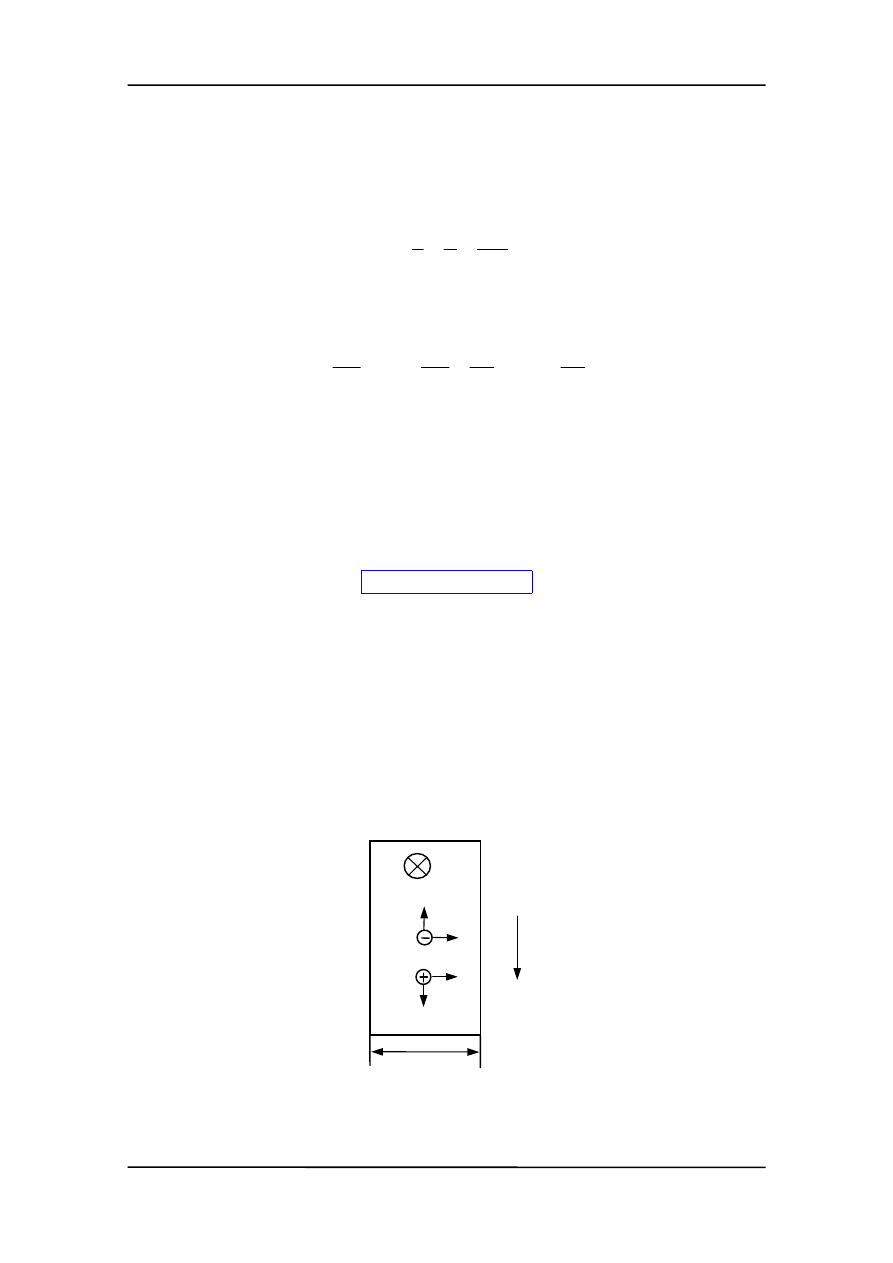
Jeżeli płytkę metalu (lub półprzewodnika) umieścimy w polu magnetycznym, pro-
stopadłym do kierunku przepływu prądu, to na ładunki będzie działała siła odchylająca
powodująca zakrzywienie torów ładunków w kierunku jednej ze ścianek bocznych
płytki. Niezależnie czy prąd jest związany z ruchem ładunków dodatnich czy ujemnych
mamy do czynienia z odchylaniem ładunków w kierunku jednej krawędzi.
I
y
x
B
v
u
v
u
F
F
d
Przesunięcie ładunków powoduje powstanie poprzecznego pola elektrycznego Halla E
H
.
To pole przeciwdziała dalszemu przesuwaniu ładunków. Pole Halla jest dane wzorem
21-9

Z. Kąkol-Notatki do Wykładu z Fizyki
d
U
E
xy
H
=
W stanie równowagi odchylające pole magnetyczne jest równoważone przez pole elek-
tryczne
qE
H
+ q(
v
u
× B) = 0
Stąd
E
H
= –
v
u
× B
Wynika stąd, że jeżeli zmierzymy E
H
i B to możemy znaleźć
v
u
.
Gdy
v
u
i B są prostopadłe to
E
H
=
v
u
B
Ponieważ:
v
u
= j/ne
więc
E
H
= (jB)/(ne)
lub
n = (jB)/(eE
H
)
Możemy wyznaczyć n.
Można też wykorzystać ten efekt do pomiaru pola magnetycznego.
21-10
Wyszukiwarka
Podobne podstrony:
Fizyka Kakol wyklad 17 id 176833
Fizyka Kakol wyklad 13 id 176831
Fizyka Kakol wyklad 14 id 176832
Fizyka Kakol wyklad 30 id 176839
Fizyka Kakol wyklad 24 id 176836
Fizyka Kakol wyklad 37 id 176843
Fizyka Kakol wyklad 22 id 176835
Fizyka Kąkol wykład 25
więcej podobnych podstron