
fale elektromagnetyczne
/
1
FALE ELEKTROMAGNETYCZNE
teoria: J.C. Maxwell
(1831 – 1879)
doświadczenie: H. Hertz
(1857 – 1894)

fale elektromagnetyczne
/
2
RÓWNANIA MAXWELLA
rot
rot
div
div
0
B
D
E
H
j
t
t
D
B
ρ
∂
∂
= −
=
+
∂
∂
=
=
r
r
r
r
r
r
r
m
H
H
B
m
F
E
D
/
10
4
/
10
85
,
8
7
0
0
12
0
0
−
−
⋅
π
=
µ
µµ
=
⋅
=
ε
εε
=
r
r
r
r
V
m
F
/
=
A
Vs
H
/
=

fale elektromagnetyczne
/
3
JEDNORODNE RÓWNANIA MAXWELLA
Dla ośrodka nie zawierającego ładunków swobodnych
(
ρ
= 0 i j = 0) jednorodne równania Maxwella
rot
rot
div
0 div
0
B
D
E
H
t
t
D
B
∂
∂
= −
=
∂
∂
=
=
r
r
r
r
r
r
fale elektromagnetyczne
/
4
RÓWNANIA MAXWELLA
t
H
y
E
x
E
t
H
x
E
z
E
t
H
z
E
y
E
t
H
rotE
z
x
y
y
o
z
x
x
y
z
∂
∂
−
=
∂
∂
−
∂
∂
∂
∂
−
=
∂
∂
−
∂
∂
∂
∂
−
=
∂
∂
−
∂
∂
∂
∂
−
=
0
0
0
µµ
µµ
µµ
µµ
t
E
y
H
x
H
t
E
x
H
z
H
t
E
z
H
y
H
t
E
rotH
z
x
y
y
z
x
x
y
z
∂
∂
=
∂
∂
−
∂
∂
∂
∂
=
∂
∂
−
∂
∂
∂
∂
=
∂
∂
−
∂
∂
∂
∂
=
0
0
0
0
εε
εε
εε
εε
z
y
x
A
A
A
z
y
x
k
j
i
A
rot
∂
∂
∂
∂
∂
∂
=
r

fale elektromagnetyczne
/
5
RÓWNANIA FALOWE
Dla
ε
= const. z jednorodnych równań Maxwella wynikają równania falowe:
2
0
0
2
0
E
E
t
εε µµ
∂
∆ −
=
∂
r
r
2
0
0
2
0
H
H
t
εε µµ
∂
∆ −
=
∂
r
r
2
∆ = ∇ ⋅∇ = ∇
r
r
We współrzędnych kartezjańskich
∂
∂
+
∂
∂
+
∂
∂
=
∆
2
2
2
2
2
2
z
y
x
fale elektromagnetyczne
/
6
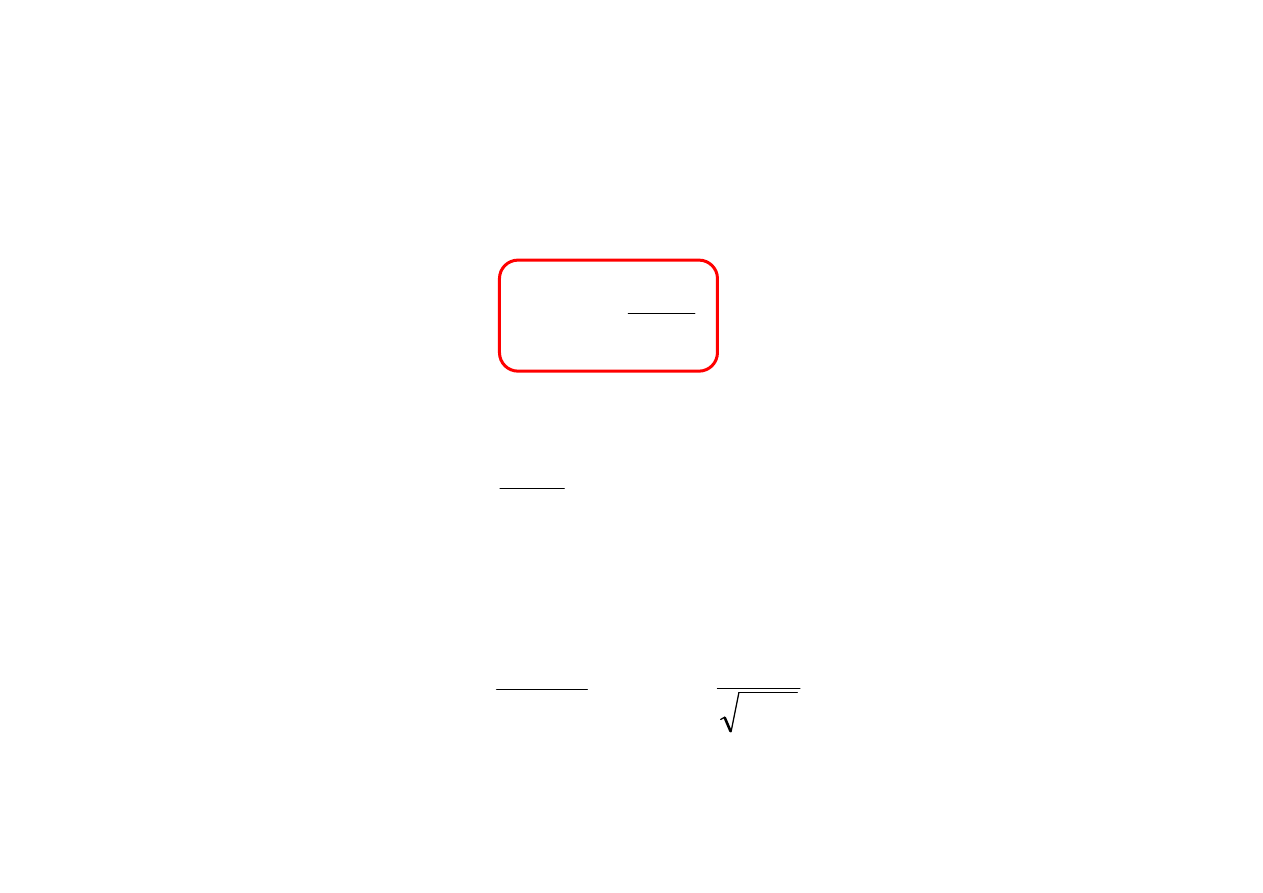
FALE ELEKTROMAGNETYCZNE
Dipol Hertza:
H
H
H
H
E
E
E
fale elektromagnetyczne
/
7
FALE ELEKTROMAGNETYCZNE
Rozwiązaniem równania falowego jest dowolna funkcja argumentu
r n
t
v
τ
⋅
= −
r r
,
która ma ciągłe drugie pochodne.
x
y
z
r n
E
f t
n r
n x
n y
n z
v
⋅
=
−
⋅ =
+
+
r r
r r
gdzie n określa kierunek, a v wartość prędkości z jaką porusza się punkt o stałej
wartości
τ
o
v
µµ
εε
=
0
2
1
0
0
1
µ
ε
=
c
.
fale elektromagnetyczne
/
8
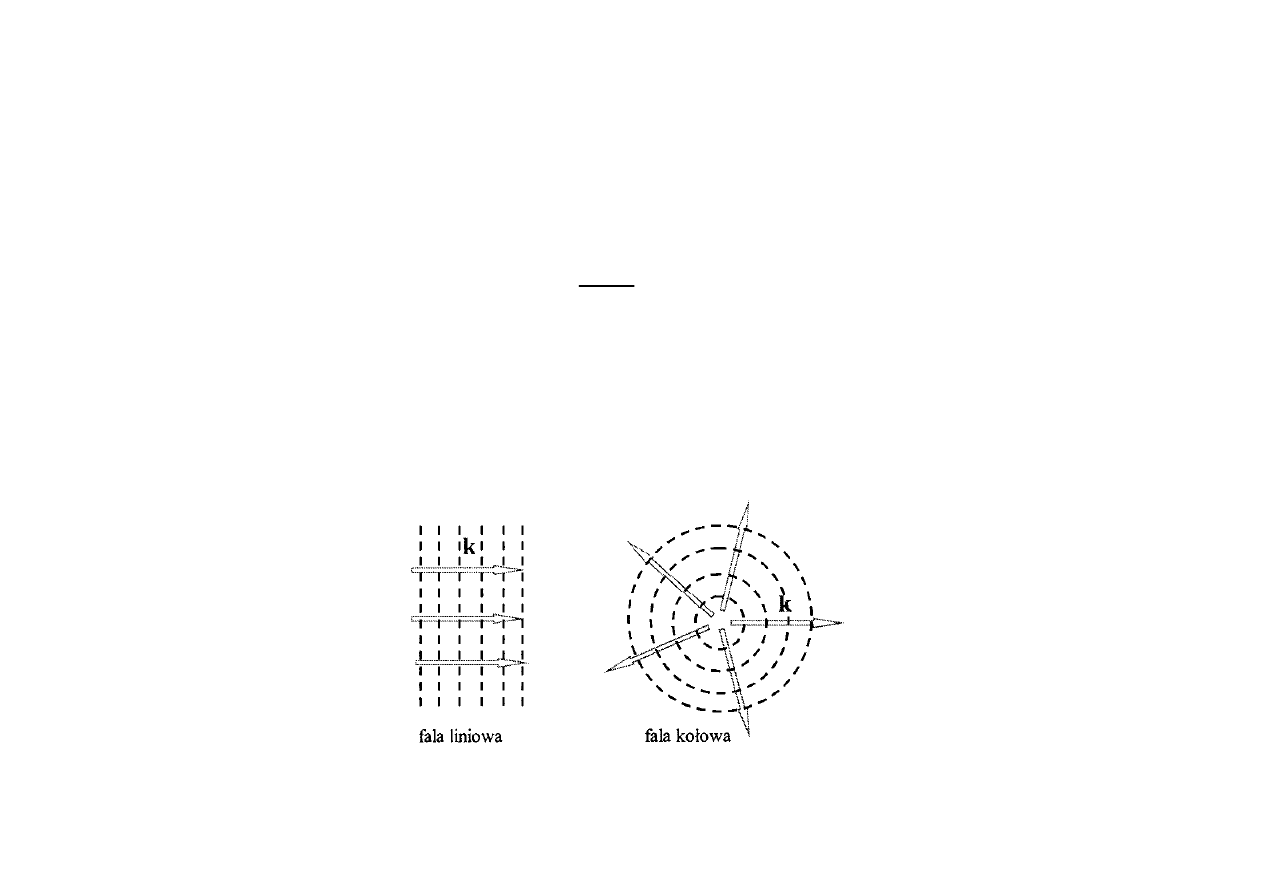
FRONT FALOWY
Punkty o stałej wartości argumentu
τ
const.
r n
t
v
τ
⋅
= −
=
r r
tworzą powierzchnie stałej fazy (fronty falowe). Dla określonej chwili czasu
(t = const.) oznacza to, że
const.
r n
⋅ =
r r
fale elektromagnetyczne
/
9
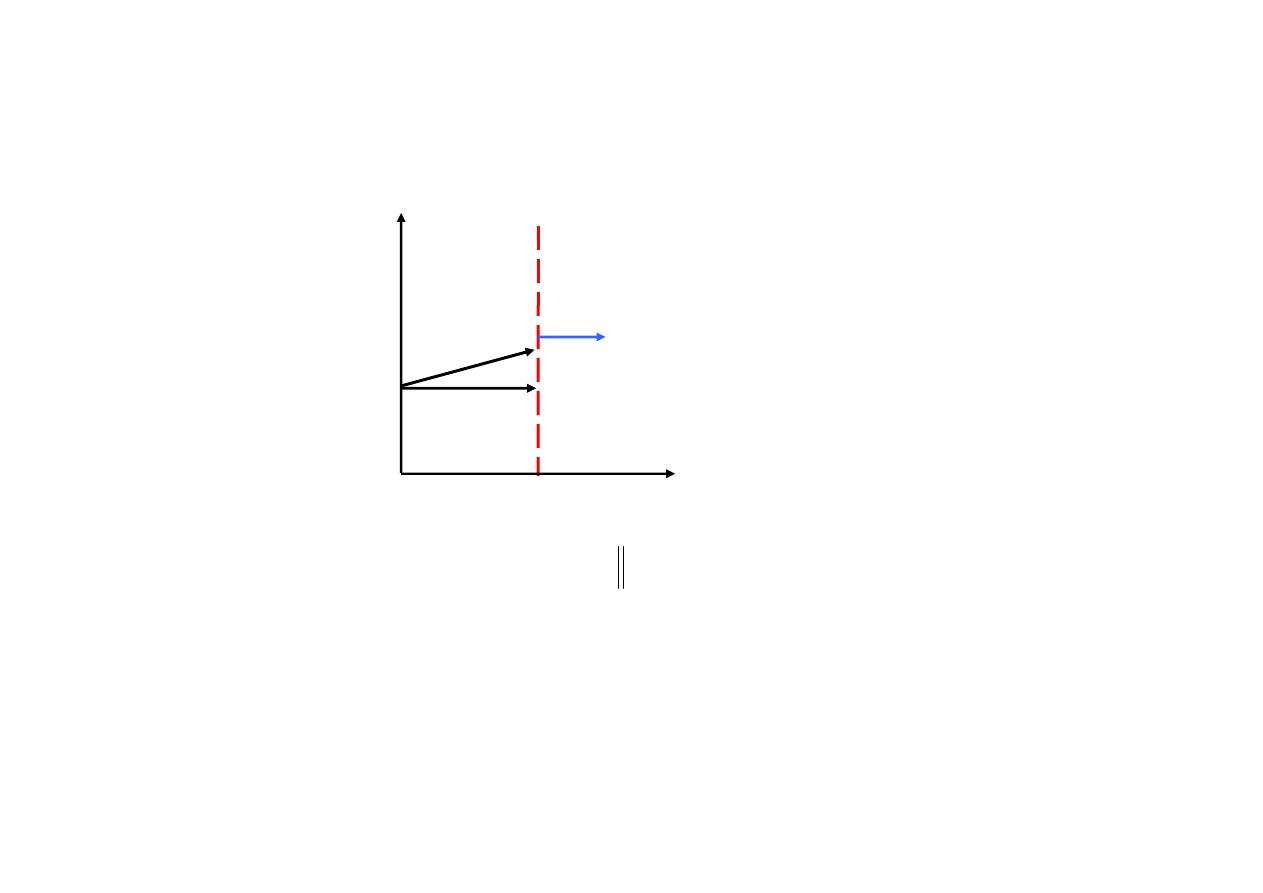
FALA PŁASKA
z
front falowy
r
r
x
r
r
x
ˆ
n
x
r
Jeżeli powierzchnie stałej fazy tworzą płaszczyzny prostopadłe do kierunku propagacji
(
x
= const.) to falę nazywa się falą płaską.
r n
x
⋅ =
r r
n
r
fale elektromagnetyczne
/
10
FALE MONOCHROMATYCZNE
Jednym z rozwiązań równania falowego jest funkcja okresowa
E
∼
cos (
ωτ
)
ω
= 2
π
/T
czyli
0
cos
E
E
t
n r
v
ω
ω
=
−
⋅
r
r
r r
(
)
0
cos
E
E
t
k r
ω
=
− ⋅
r
r
r
r
gdzie oznacza wektor falowy
k
r
k
n
v
ω
=
r
r
0
0
µµ
εε
ω
=
k
ε
=
ε
(
ω
)
- dyspersja ośrodka.

fale elektromagnetyczne
/
11
FALE MONOCHROMATYCZNE
(
)
0
cos
E
E
t
k r
ω
=
− ⋅
r
r
r
r
W postaci zespolonej
(
)
(
)
*
0
0
i
t k r
i
t k r
E
E e
E e
ω
ω
− ⋅
−
− ⋅
=
+
r
r
r
r
r
r
r
lub w skrócie:
(
)
0
. .
i
t k r
E
E e
c c
ω
− ⋅
=
+
r r
r
r
fale elektromagnetyczne
/
12
KIERUNKI PÓL E i H
Dla fali płaskiej propagującej się w kierunku x - pochodne po y i po z są równe 0
0
0
y
z
y
z
o
x
H
E
x
t
E
H
x
t
H
µµ
µµ
∂
∂
=
∂
∂
∂
∂
= −
∂
∂
=
0
0
0
y
z
y
z
x
H
E
x
t
E
H
x
t
E
εε
εε
∂
∂
=
∂
∂
∂
∂
= −
∂
∂
=
Układ równań Maxwella rozdziela się na dwa niezależne podukłady:
0
y
z
y
z
o
H
E
x
t
E
H
x
t
µµ
µµ
∂
∂
=
∂
∂
∂
∂
= −
∂
∂
0
0
y
z
y
z
H
E
x
t
E
H
x
t
εε
εε
∂
∂
=
∂
∂
∂
∂
= −
∂
∂
dwie pary składowych
(E
z
, H
y
)
lub
(E
y,
H
z
)
fale elektromagnetyczne
/
13
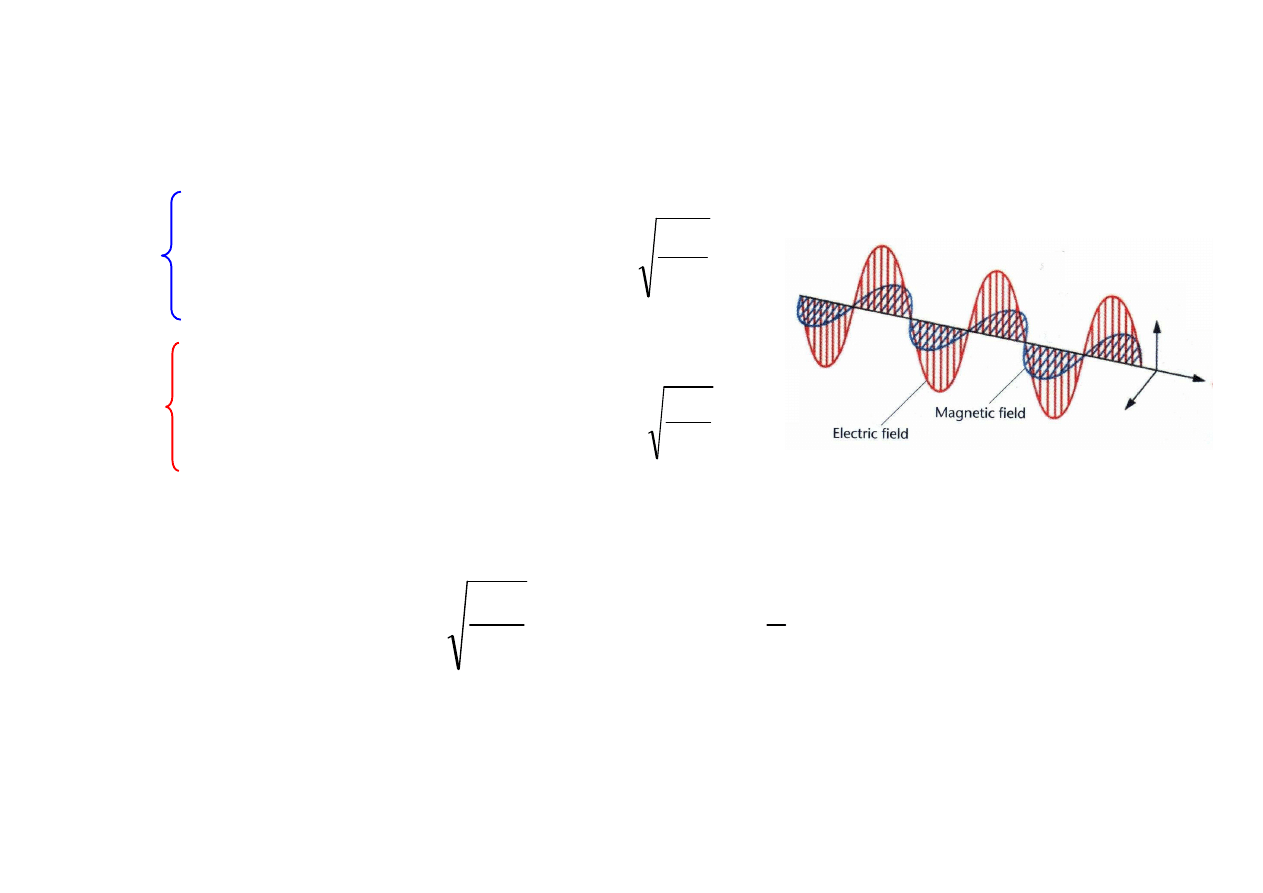
MONOCHROMATYCZNE FALE PŁASKIE
(
)
(
)
cos
cos
0
0
kx
t
H
H
kx
t
E
E
z
y
−
ω
=
−
ω
=
r
r
r
r
0
0
0
0
y
z
E
H
µµ
εε
=
(
)
(
)
cos
cos
0
0
kx
t
H
H
kx
t
E
E
y
z
−
ω
=
−
ω
=
r
r
r
r
0
0
0
0
z
y
E
H
µµ
εε
−
=
Ogólnie
E
n
v
B
E
n
H
r
r
r
r
r
r
×
=
×
µµ
εε
=
1
lub
0
0
Znając pole elektryczne można wyznaczyć pole magnetyczne
fale elektromagnetyczne
/
14
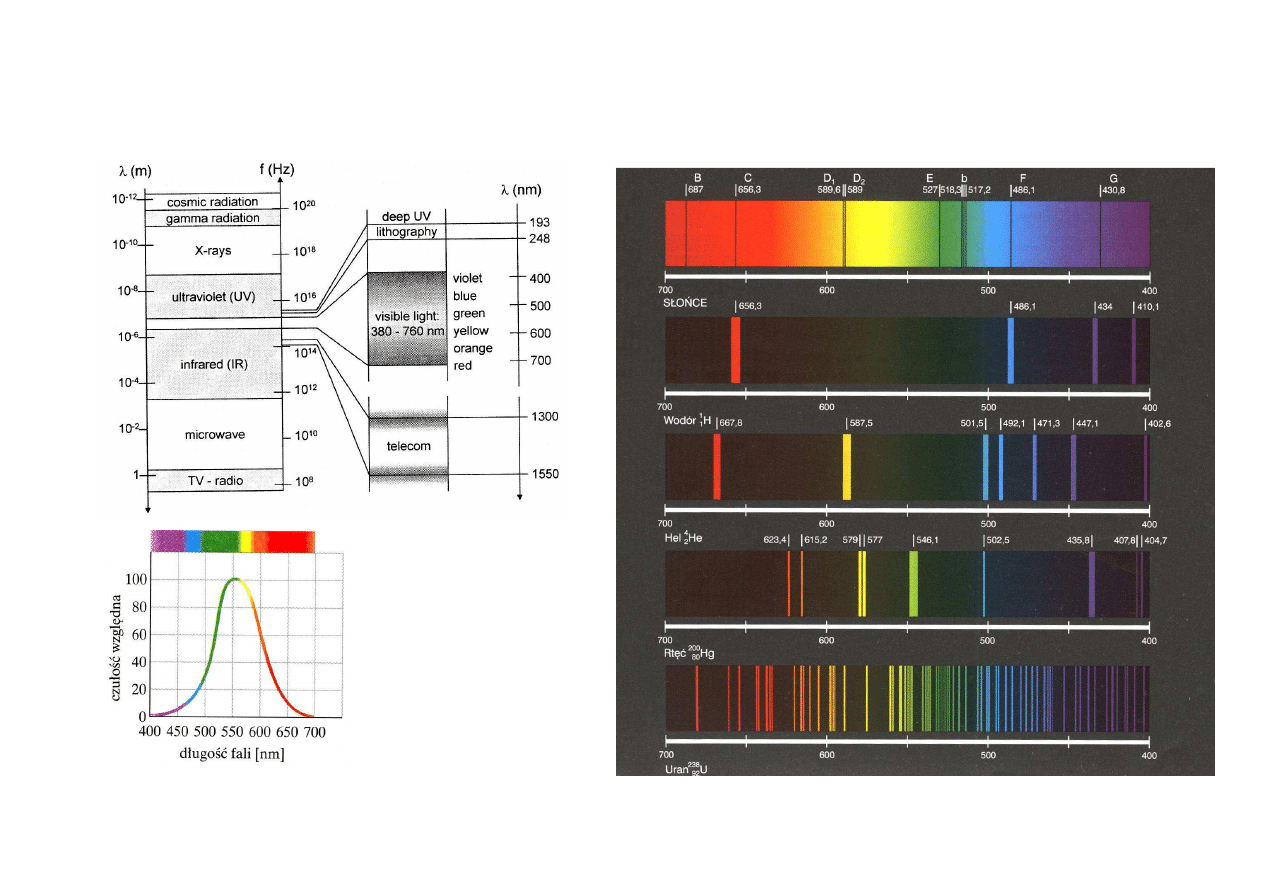
WIDMO FAL ELEKTROMAGNETYCZNYCH
Czułość oka ludzkiego
fale elektromagnetyczne
/
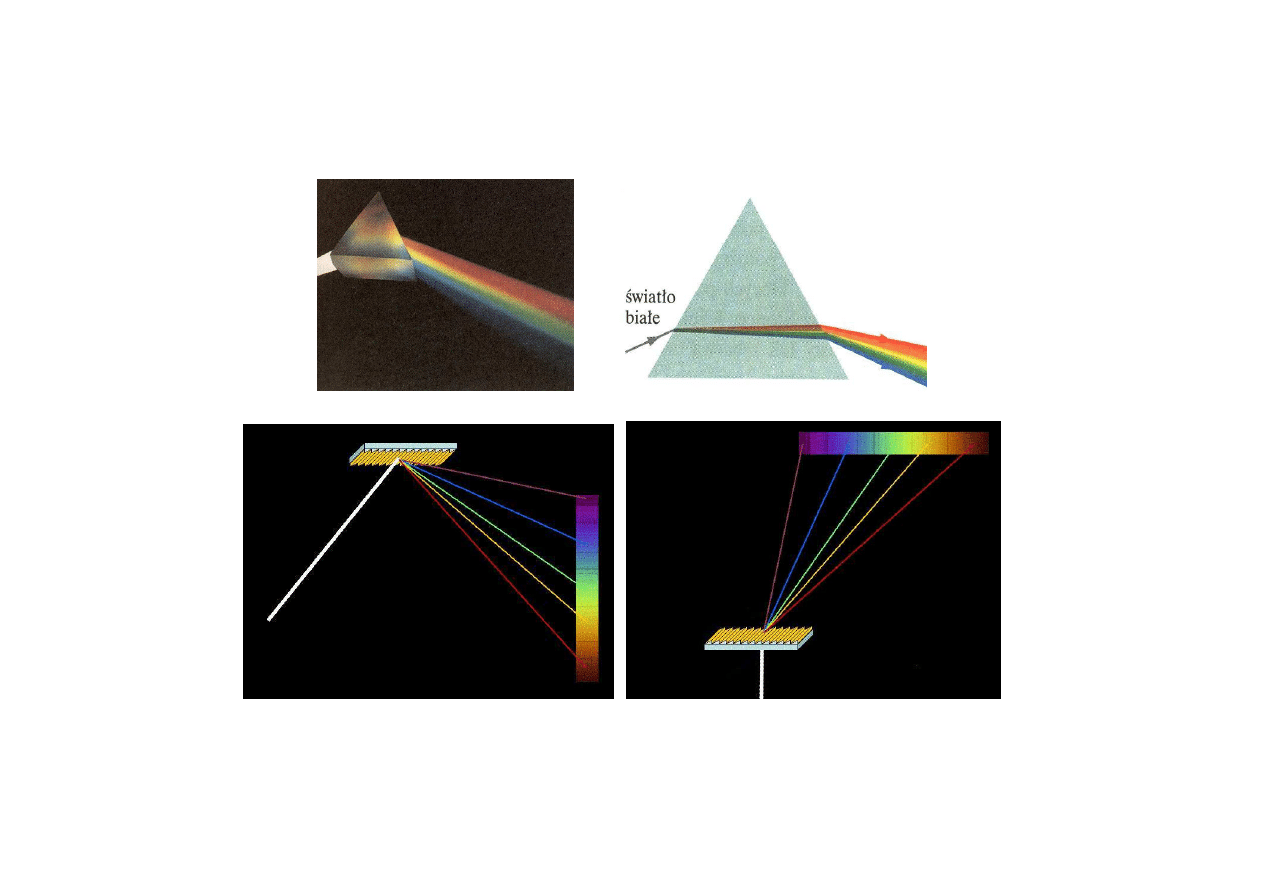
15
ROZSZCZEPIENIE ŚWIATŁA
Siatka odbiciowa i transmisyjna
fale elektromagnetyczne
/
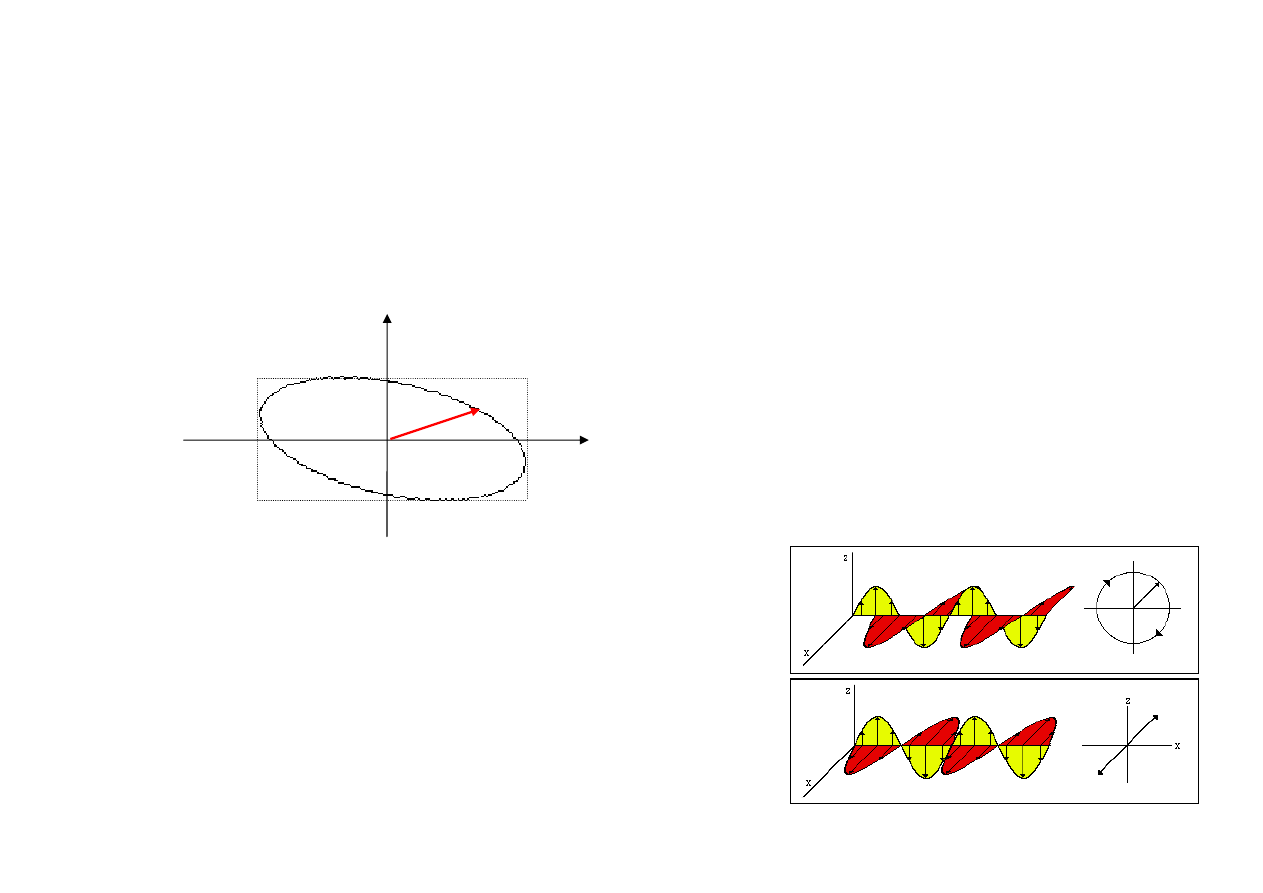
16
POLARYZACJA FAL
(
)
(
)
2
2
1
1
cos
ˆ
cos
ˆ
δ
+
−
ω
=
δ
+
−
ω
=
kx
t
A
z
E
kx
t
A
y
E
z
y
r
r
δ
1
-
δ
2
przesunięcie fazowe
fala spolaryzowana kołowo
A
1
= A
2
i
δ
1
-
δ
2
= (2m + 1)
π
/2 m = 0,
±
1, ...
fala spolaryzowana liniowo
A
1
= 0 lub A
2
= 0 lub
δ
1
-
δ
2
= m
π
fale elektromagnetyczne
/
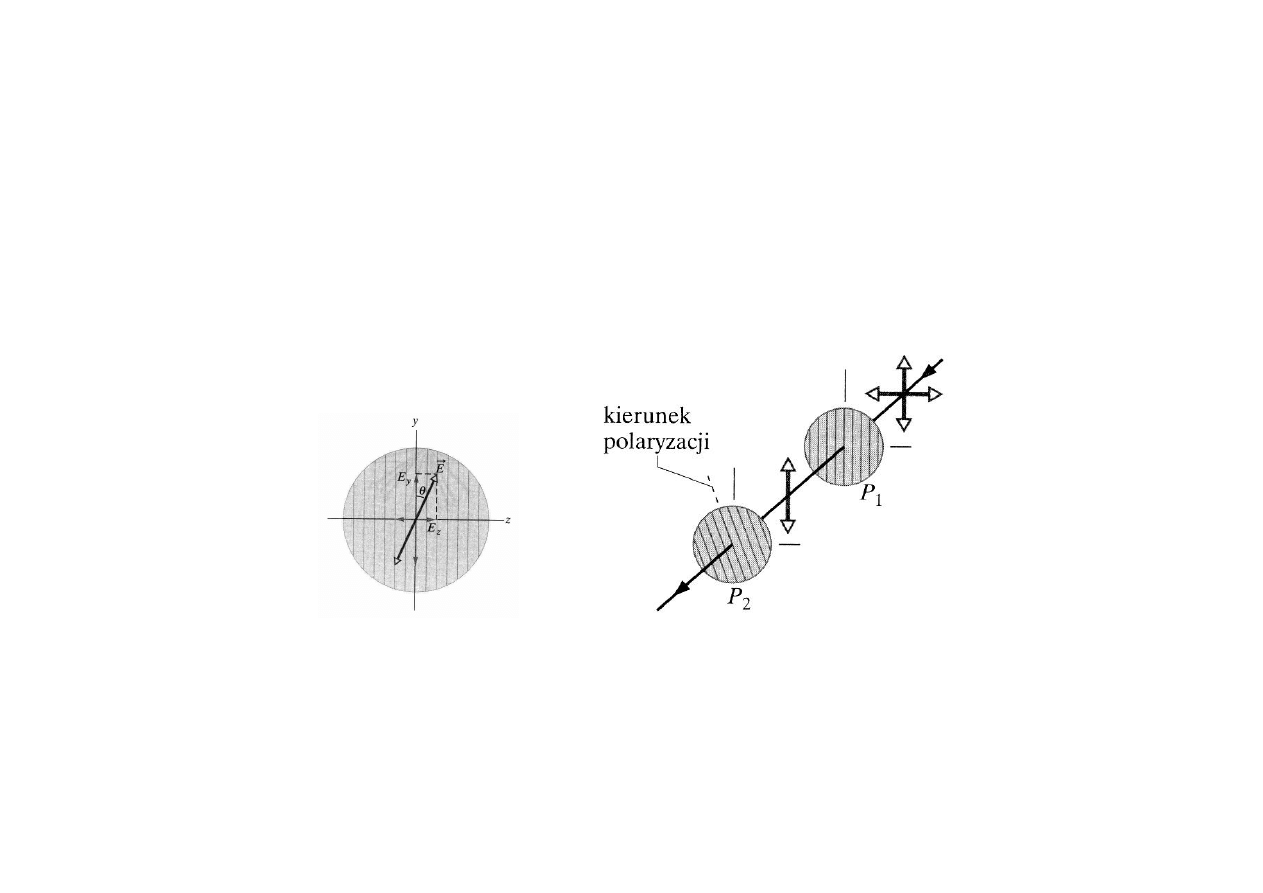
17
POLARYZOWANIE ŚWIATŁA
metody uzyskania fal spolaryzowanych np. liniowo
•
emisja selektywna
•
absorpcja selektywna
•
selektywne odbicie
•
dwójłomność
Po przejściu przez polaryzator P
E = E
0
cos
θ
θ
- kąt między osią łatwego przepuszczania polaryzatora, a kierunkiem natężenia pola
elektrycznego fali świetlnej.
POLARYZATOR
fale elektromagnetyczne
/
18
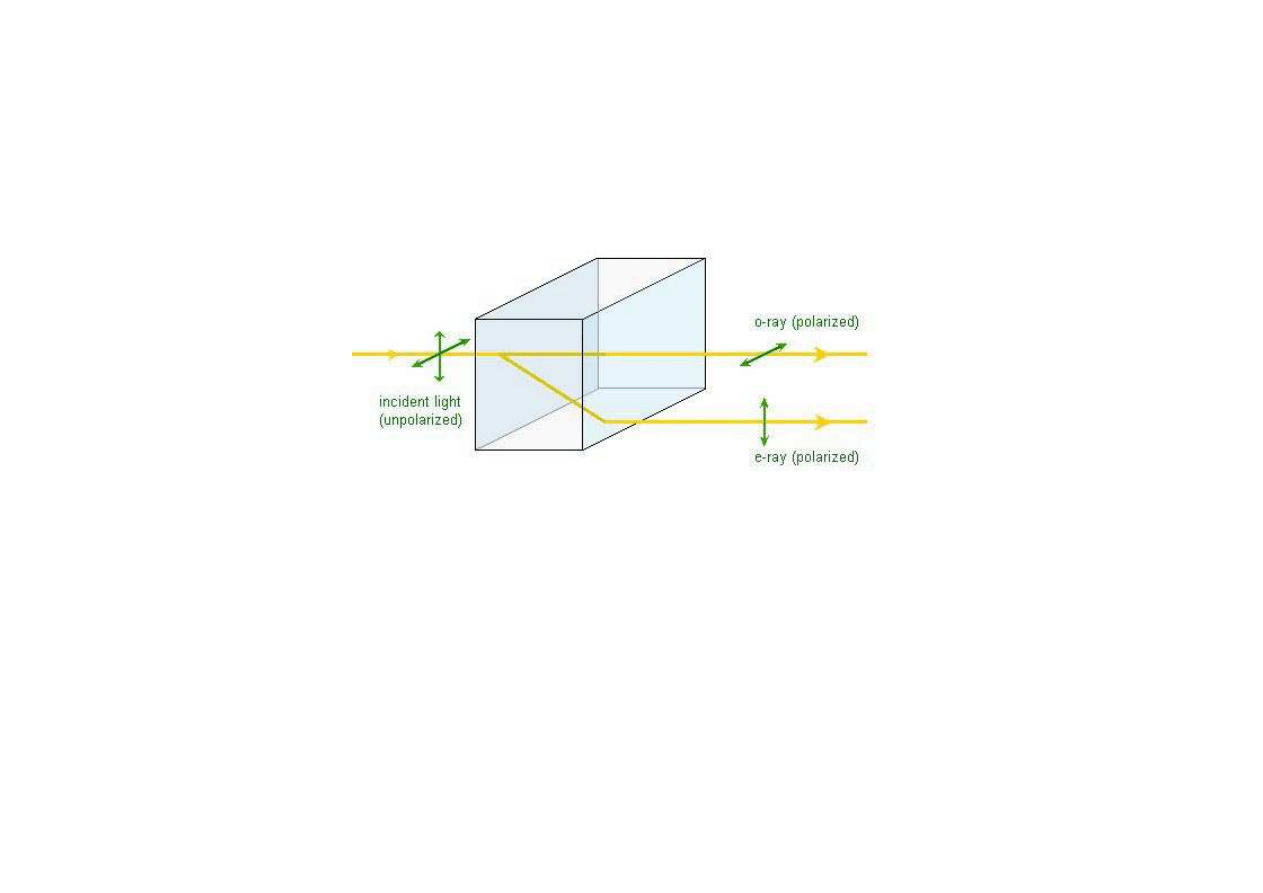
KRYSZTAŁ DWÓJŁOMNY

fale elektromagnetyczne
/
19
ENERGIA FALI ELEKTROMAGNETYCZNEJ
•
Gęstość energii
2
0
.
2
1
2
1
E
D
E
e
el
εε
=
⋅
=
r
r
2
0
2
1
2
1
H
B
H
e
m
µµ
=
⋅
=
r
r
e
e
e
E
H
m
el
=
+
=
+
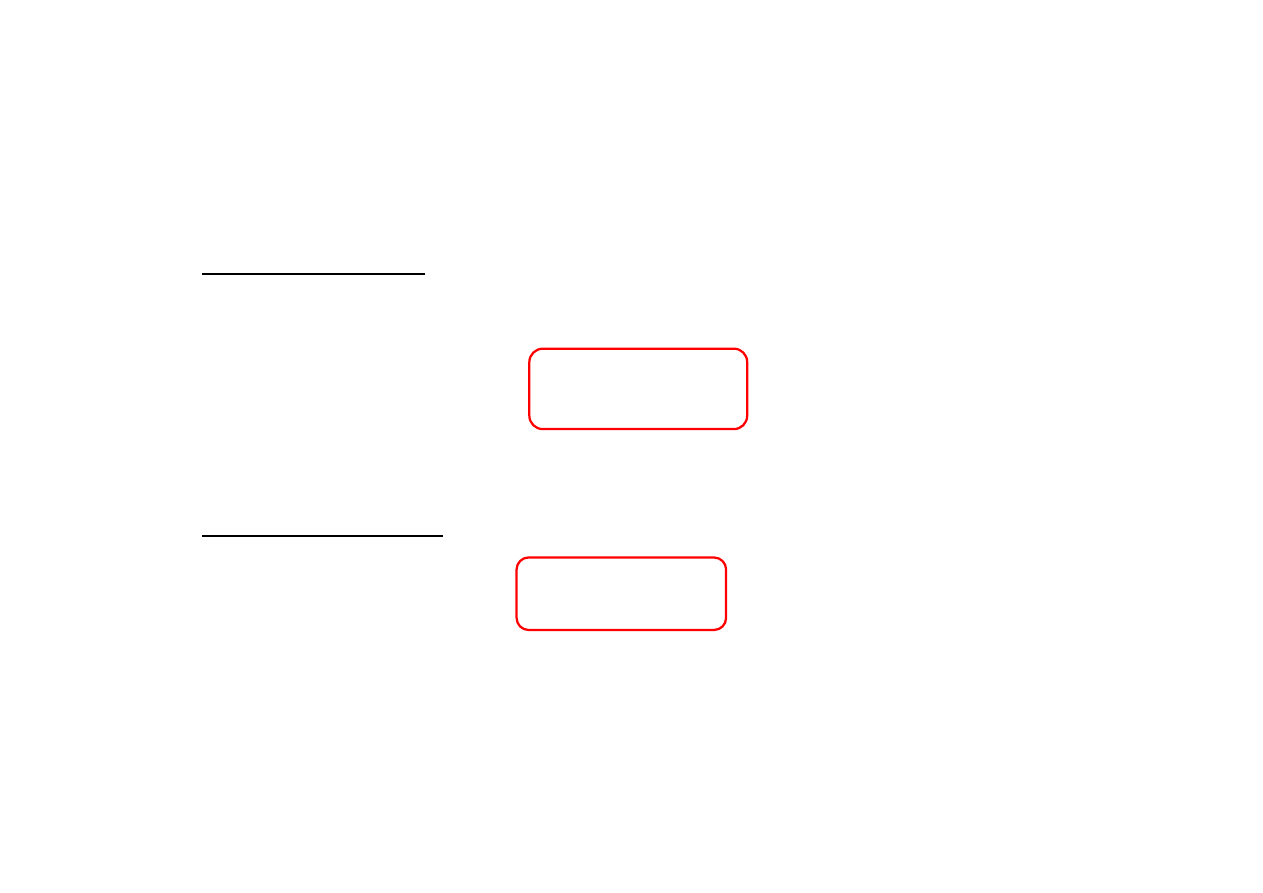
1
2
0
2
0
2
(
)
εε
µµ
2
0
E
e
εε
=
fale elektromagnetyczne
/
20
ENERGIA FALI ELEKTROMAGNETYCZNEJ
•
Gęstość energii
2
0
E
e
εε
=
•
Strumień energii
S
E H
= ×
r
r
r
wektor Poyntinga
:
fale elektromagnetyczne
/
21
NATĘŻENIE FALI
0
1
T
sr
I
S
Sdt
T
=
=
∫
r
Dla fali płaskiej spolaryzowanej liniowo
H
E
=
εε
µµ
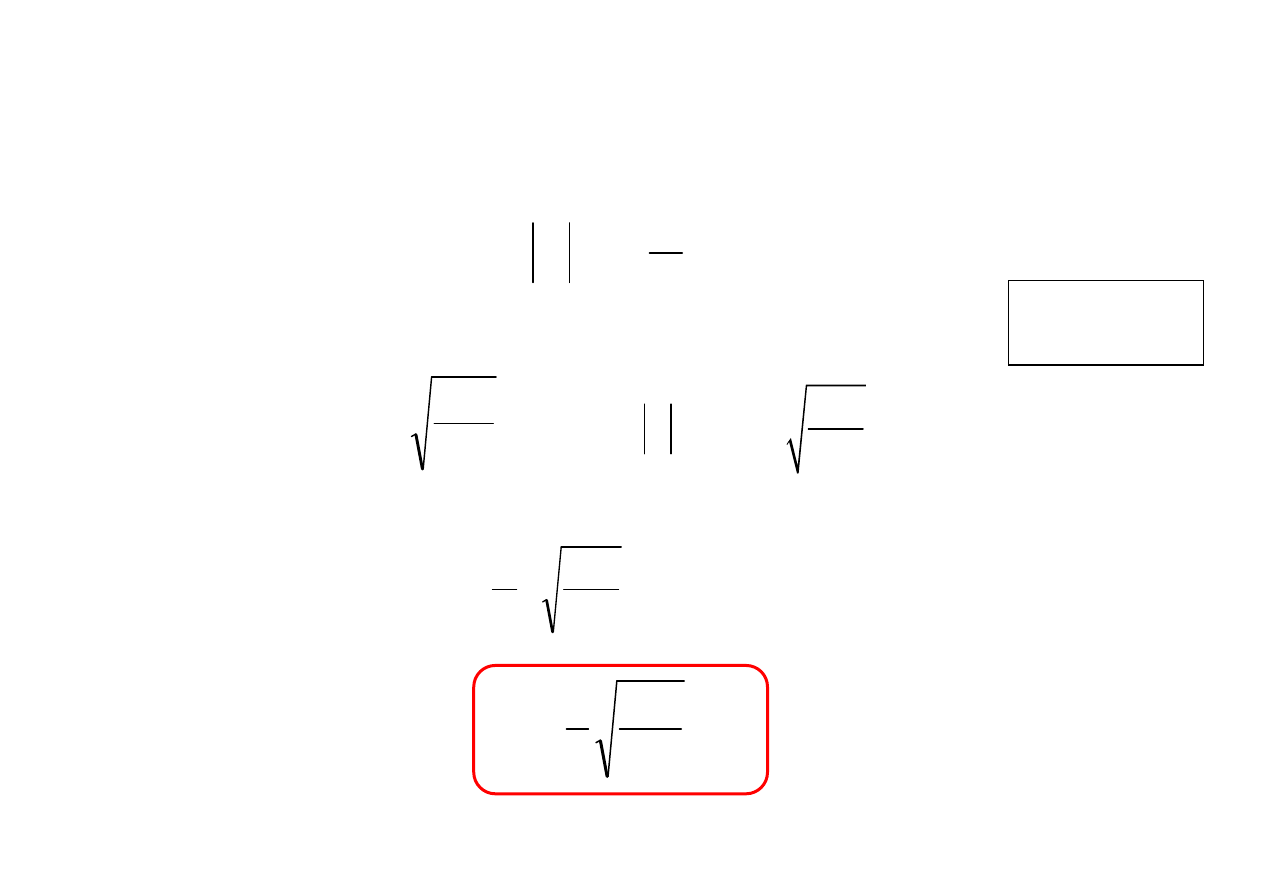
0
0
2
0
0
S
EH
E
εε
µµ
=
=
r
dla
t
T
>>
dt
kx
t
E
T
I
T
)
(
cos
1
2
2
0
0
0
0
−
=
∫
ω
µµ
εε
2
0
0
0
2
1
E
I
µµ
εε
=
S
E
H
= ×
r
r
r
Wyszukiwarka
Podobne podstrony:
16 Fale elektromagnetyczne
Fizyka 1 23 fale elektromagnetyczne 2013 r
fale elektromagnetyczna fizyka sprawdzian klasa 2
fale elektromagnetyczne fizyka
Fale elektromagnetyczne(1), nauka, fizyka, FIZYKA-ZBIÓR MATERIAŁÓW
Fale elektromagnetyczne ll(1), nauka, fizyka, FIZYKA-ZBIÓR MATERIAŁÓW
Fale Elektromagnetyczne, Sprawozdania - Fizyka
Fale elektromagnetyczne- fizyka, Gimnazjum
Fale elektromagnetyczne, fizyka
,fizyka2,Fale elektromagnetyczne
fizyka drgania i fale pr klucz
Fale Elektromagnetyczne
Fizyka 1 15 fale sprężyste
Drgania i fale elektromagnetyczne
35 Fale elektromagnetyczne i ich polaryzacja
Fale elektromagnetyczne czyli czym naprawdę jest światło
Fizyka Uzupelniajaca Prad elektryczny I id 177229
więcej podobnych podstron