1

Wiktor Wysocki
AiR III Mechanika

Nierównomierność biegu maszyny, dobór koła zamachowego

Nierównomierność biegu maszyny

W ruchu ustalonym maszyny, to znaczy kiedy pracuje ona w swoich warunkach

znamionowych, praca sił napędów równoważy pracę sił oporów (maszyna kręci się ze stałą
prędkością obrotową). Jeśli jednak rozpatrzymy ten ruch szczegółowo to okazuje się, że w
obrębie jednego cyklu pracy maszyny występują pewne wahania prędkości jej elementów.
Wahania te powtarzają się okresowo w każdym cyklu i powodowane są okresowymi
zmianami uogólnionych sił napędzających oraz sił oporu, a także zmianą zredukowanego
momentu bezwładności maszyny. Mogą być nieznaczne, dla maszyn wirnikowych, albo dość
duże jak w przypadku jednocylindrowych maszyn tłokowych. Do określenia parametrów
wspomnianego ruchu okresowego wystarczy obserwować zmianę prędkości (kątowej lub
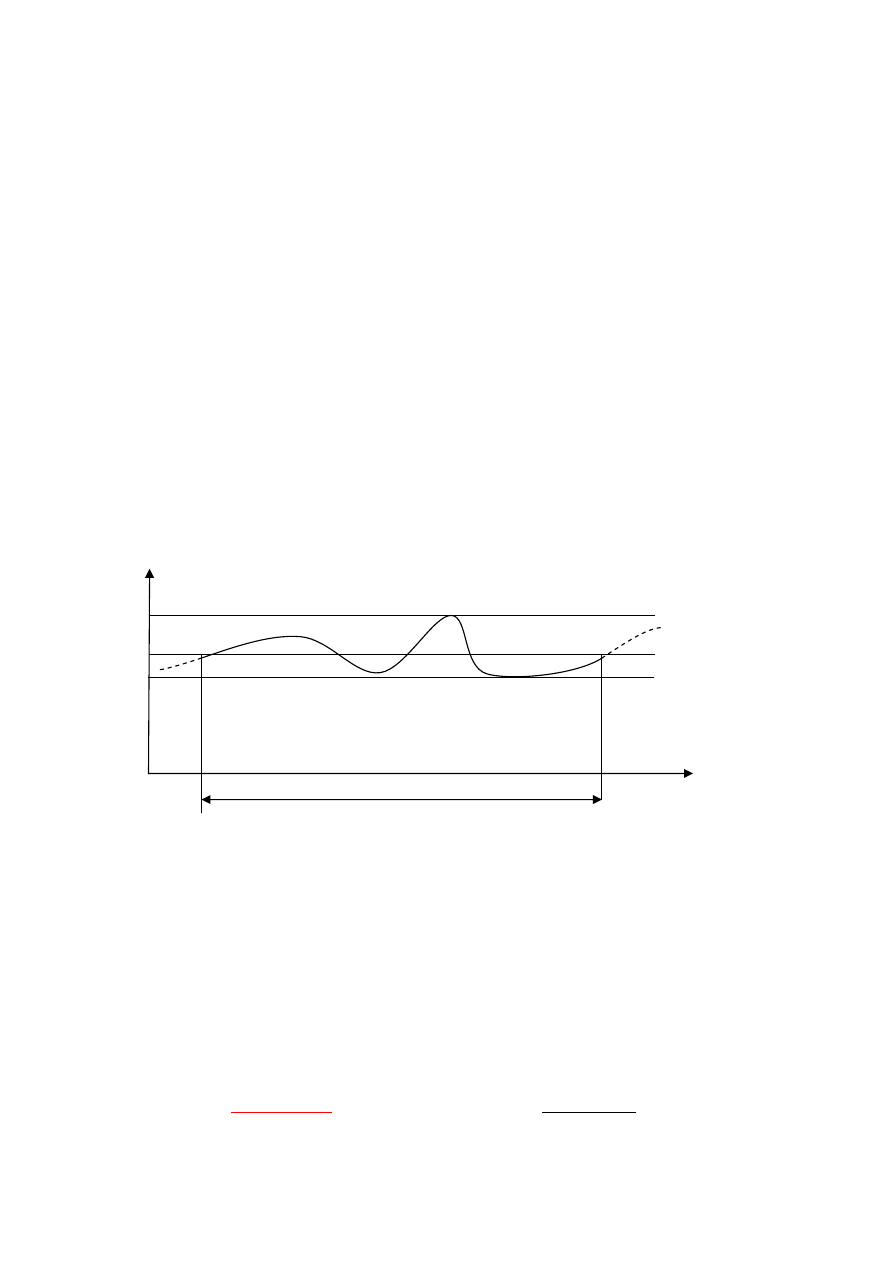
liniowej) wybranego członu maszyny (obracającego się względem osi redukcji). Na wykresie
pokazano przykładowy przebieg prędkości kątowej jednego z elementów ruchomych pewnej
maszyny.

ω(φ)

ω

max

ω

śr

ω(0)

ω(φ

c

)

ω

min

φ

φ

c

Wykres 1

Dla jednego cyklu pracy musi zachodzić

ܮ

௖

= ܮ

௕

oraz

߱ሺ0ሻ = ߱ሺ߮

௖

ሻ

(1)

gdzie:
L

c

– praca sił czynnych (napędowych)

L

b

– praca sił biernych (oporu)

Miarą zmienności prędkości w ruchu okresowym ustalonym jest stopień (współczynnik)
nierównomierności biegu δ maszyny

ߜ =

߱

௠௔௫

− ߱

௠௜௡

߱

ś௥

lub

ߜ =

ݒ

௠௔௫

− ݒ

௠௜௡

ݒ

ś௥

(2)

2

gdzie:
ω

max

, v

max

– prędkość maksymalna kątowa i liniowa

ω

min

, v

min

– prędkość minimalna kątowa i liniowa

ω

ś

r

, v

ś

r

– prędkość średnia kątowa i liniowa

Jeżeli znamy przebieg prędkości członu w cyklu ruchu ustalonego (jak na wykresie 1) to ω

ś

r

możemy obliczyć ze wzoru

߱

ś௥

=

1

ܶ

௖

න ߱ሺ߮ሻ݀ݐ

்

೎

଴

lub

߱

ś௥

=

1

߮

௖

න ߱ሺ߮ሻ݀߮

ఝ

೎

଴

(3)

gdzie:
T

c

– okres cyklu ruchu ustalonego

φ

c

– przemieszczenie kątowe członu podczas trwania cyklu

najczęściej przyjmuje się jednak

߱

ś௥

=

߱

௠௔௫

+ ߱

௠௜௡

2

(4)

wtedy po odpowiednich przekształceniach otrzymujemy

߱

௠௔௫

= ߱

ś௥

ሺ1 +

ߜ

2ሻ

lub

߱

௠௜௡

= ߱

ś௥

ሺ1 −

ߜ

2ሻ

(5)

a także po pomnożeniu stronami (4) przez

ሺ߱

௠௔௫

+ ߱

௠௜௡

ሻ i wykorzystaniu (5) otrzymujemy

równoważny wzór na współczynnik nierównomierności biegu

ߜ =

߱

௠௔௫

ଶ

− ߱

௠௜௡

ଶ

2߱

ś௥

ଶ

(6)

który będzie przydatny przy następnym wyprowadzeniu

Korzystając ze wzoru na energię kinetyczną w ruchu obrotowym, zapisujemy równanie ruchu
maszyny w postaci energii kinetycznej dla części cyklu zawartego miedzy ω

max

a

ω

min

przy

założeniu, że zredukowany moment bezwładności całej maszyny J

zr

nie ulega zmianie

ܧ

௞

=

ܫ߱

ଶ

2

(7)

ܧ

௞

=

1

2 ܬ

௭௥

ሺ߱

௠௔௫

ଶ

− ߱

୫୧୬

ଶ

ሻ = ܹ = ܮ

௖

− ܮ

௕

= ܮ

௠௔௫

(8)

gdzie:
L

max

– największa nadwyżka pomiędzy pracą sił czynnych a pracą sił biernych w cyklu pracy

ustalonej

3

dzielimy obie strony równania (8) przez

߱

ś௥

ଶ

i otrzymujemy

ܬ

௭௥

ሺ߱

௠௔௫

ଶ

− ߱

୫୧୬

ଶ

ሻ

2߱

ś௥

ଶ

=

ܮ

௠௔௫

߱

ś௥

ଶ

(9)

czyli

ߜ =

ܮ

௠௔௫

ܬ

௭௥

߱

ś௥

ଶ

(10)

Pamiętajmy że powyższy wzór służy do wyznaczania współczynnika δ tylko wtedy gdy
moment J

zr

jest stały.

Z wzoru (10) wynika także bardzo ważny wniosek, otóż aby ograniczyć

nierównomierność biegu maszyny należy zwiększyć jej zredukowany moment bezwładności.
Czyni się to poprzez łączenie maszyn w odpowiednie układy (np. silniki spalinowe są
kojarzone w układy wielotłokowe) oraz poprzez dodanie odpowiedniej masy do maszyny
zwiększającej jej moment bezwładności. Tym elementem jest właśnie koło zamachowe.
Dzięki zwiększeniu zredukowanego momentu bezwładności maszyny, wpływa ono
wyrównująco na prędkość maszyny w czasie każdego cyklu ruchu. Kumuluje energię w
okresie przewagi sił napędowych i oddaje w okresie przewagi sił oporów. To pozwala np.
obniżyć znacznie konieczny moment napędowy i moc silnika w maszynach w których opór
użyteczny działa tylko przez część cyklu, niestety jednak kosztem zwiększenia współczynnika
δ. Przykładem takiej maszyny są nożyce mechaniczne. Energia jest akumulowana w kole
zamachowym gdy nożyce są rozwierane i nie występuj opór ciętego materiału.

Nadmierne wahania prędkości są oczywiście niekorzystne dla procesów

technologicznych, a ponadto powodują wzrost obciążeń dynamicznych oraz oporów ruchu. W
związku z tym wartość δ powinna być dostosowana do potrzeb danego procesu
technologicznego. Dla przykładu współczynnik nierównomierności biegu może się wahać

od

1 5

ൗ dla wspomnianych nożyc mechanicznych oraz pomp do 1 300

ൗ

dla generatorów

elektrycznych.

Dobór koła zamachowego

Pojawia się problem doboru oraz umiejscowienia odpowiedniego koła zamachowego,

tak aby uzyskać żądaną wartość współczynnika δ. Co do umiejscowienia koła to może się
ono znaleźć na różnych członach układu napędowego
- na wale silnika
- na jednym z członów przekładni
-na wale maszyny roboczej

Najlepiej jest umieszczać koło zamachowe na tym zespole układu napędowego, który

jest źródłem nierównomierności biegu. Czasem jednak w przypadku gdy powodem
nierównomierności biegu jest maszyna robocza, osadzenie na jej wolnoobrotowym wale, koła
zamachowego będzie skutkowało dużymi jego rozmiarami. Wtedy należy jednak umieścić
koło zamachowe na szybkoobrotowym wale silnika i liczyć się z dodatkowymi drganiami
mechanicznymi.

Gdy mamy już umiejscowione koło zamachowe w zespole napędowym należy dobrać

jego wielkość, a w zasadzie jego moment bezwładności. Służą do tego różne metody.

4

- metody dokładne, oparte na znajomości przebiegu momentu zredukowanego sił napędowych
oraz sił oporu w czasie cyklu ruchu ustalonego
- metody pośrednie, oparte wyłącznie na wykresach momentu sił napędowych i sił oporu
- metody numeryczne, oparte na numerycznych algorytmach rozwiązujących równania
różniczkowe opisujące momenty sił

Zajmiemy się przypadkiem drugim. Po wprowadzeniu do układu koła zamachowego mamy
nowy wzór na moment zredukowany układu

ܬ

௭௥

= ܬ

௭௥ெ

+ ܬ

௄

(11)

gdzie:
J

zr

– całkowity zredukowany moment bezwładności układu wraz z kołem zamachowym

J

zrM

– zredukowany moment bezwładności układu bez koła zamachowego

J

K

– moment bezwładności koła zamachowego

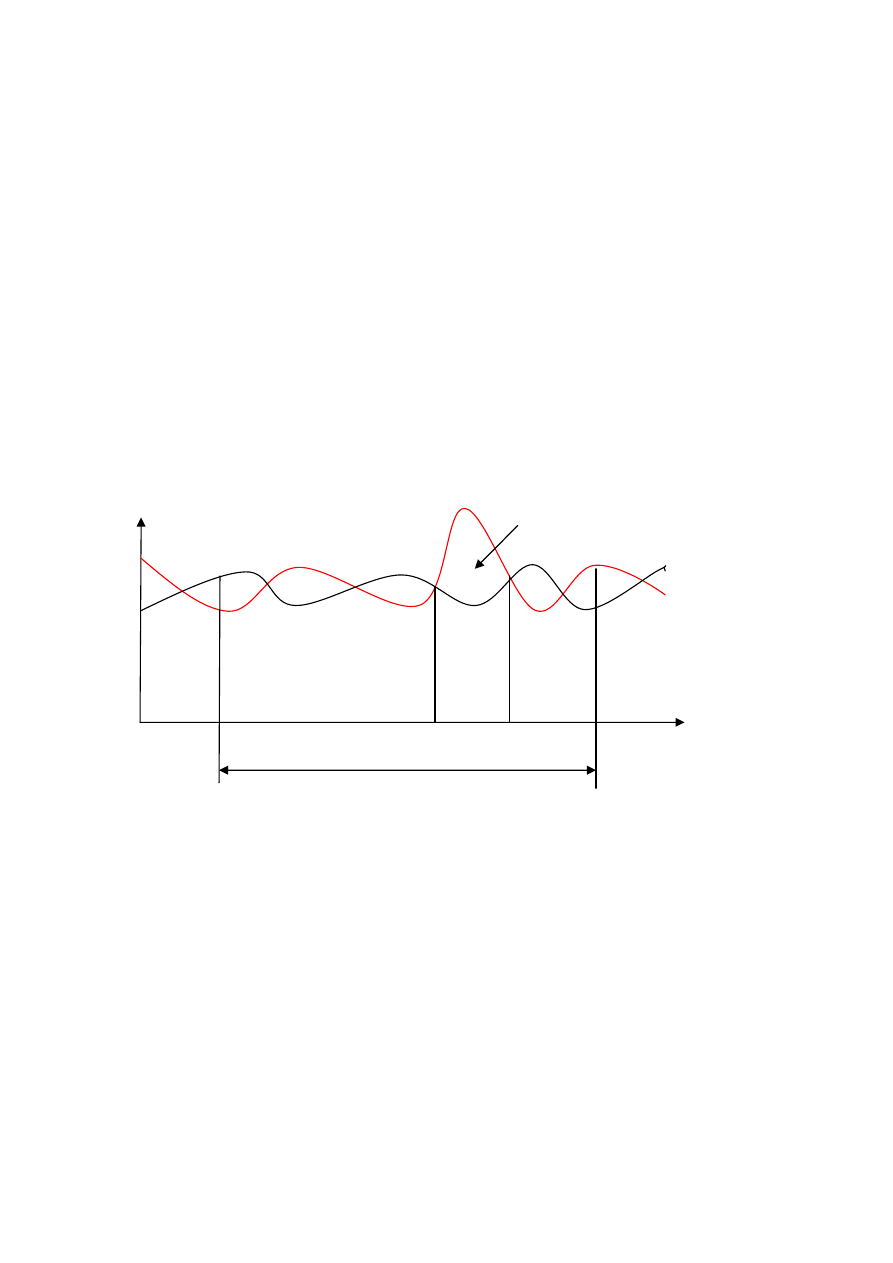
Mamy także dany wykres momentów sił napędowych i sił oporu

L

max

M

c

⊕

⊖ ⊕ ⊖ ⊖ ⊕

M

b

ω

min

= ω(φ

1

)

ω

max

= ω(φ

2

)

φ

1

φ

2

φ

φ

c

Wykres 2

Na wykresie zaznaczono pewne obszary w których występują nadwyżki pracy jednego

z momentów sił. W polach oznaczonych

⊕ praca momentów sił napędowych jest większa niż

praca momentów sił oporu (człon zwiększa swoją energie kinetyczna - prędkość obrotową)
natomiast w obszarach oznaczonych

⊖ odwrotnie (człon zmniejsza swoja energie kinetyczną

– prędkość obrotową). W przedziale cyklu którego pole jest największe, następuję największa
zmiana prędkości obrotowej członu. O nierównomierności biegu decyduje zatem największe
pole na wykresie (niezależnie od znaku) które zostało oznaczone przez L

max

. Przystępujemy

do obliczeń.

ܮ

௠௔௫

= න [ܯ

௖

ሺ߮ሻ

ఝ

మ

ఝ

భ

− ܯ

௕

ሺ߮ሻ]݀߮

(12)

natomiast z równowartości energii możemy zapisać

5

1

2 ሺܬ

௭௥ଶ

߱

௠௔௫

ଶ

− ܬ

௭௥ଵ

߱

௠௜௡

ଶ

ሻ = ܮ

௖

− ܮ

௕

= ܮ

௠௔௫

(13)

Równanie to jest podobne do zapisanego uprzednio (8) lecz tym razem mamy

ܬ

௭௥ଵ

= ܬ

௭௥ெଵ

+ ܬ

௄

oraz

ܬ

௭௥ଶ

= ܬ

௭௥ெଶ

+ ܬ

௄

(14)

gdzie:

ܬ

௭௥ெଵ

- zredukowany moment bezwładności maszyny w położeniu φ

1

ܬ

௭௥ெଶ

- zredukowany moment bezwładności maszyny w położeniu φ

2

mamy

ܮ

௠௔௫

=

ܬ

௞

ሺ߱

௠௔௫

ଶ

− ߱

୫୧୬

ଶ

ሻ

2

+

ܬ

௭௥ெଶ

߱

௠௔௫

ଶ

− ܬ

௭௥ெଵ

߱

௠௜௡

ଶ

2

(15)

dzieląc (15) stronami przez

߱

ś௥

ଶ

oraz wykorzystując (5) otrzymujemy

ܮ

௠௔௫

߱

ś௥

ଶ

= ܬ

௄

ߜ +

ܬ

௭௥ெଶ

൬1 + ߜ + ߜ

ଶ

4 ൰ − ܬ

௭௥ெଵ

൬1 − ߜ + ߜ

ଶ

4 ൰

2

(16)

δ jest ułamkiem więc możemy pominąć element

ఋ

మ

ସ

ze względu na małą wartość i wyznaczyć

J

K

ze wzoru (16)

ܬ

௄

=

ܮ

௠௔௫

߱

ś௥

ଶ

ߜ −

ܬ

௭௥ெଶ

ሺ1 + ߜሻ − ܬ

௭௥ெଵ

ሺ1 − ߜሻ

2

(17)

W przypadku gdy moment bezwładności maszyny bez koła zamachowego zmienia się w
małym zakresie można przyjąć

ܬ

௭௥ெଵ

= ܬ

௭௥ெଶ

= ܬ

௭௥ெ௠௜௡

(18)

wtedy wzór (17) uprości się do postaci

ܬ

௄

=

ܮ

௠௔௫

߱

ś௥

ଶ

ߜ − ܬ

௭௥ெ௠௜௡

(19)

Jeśli

ܬ

௭௥ெ௠௜௡

jest mały to można go pominąć w obliczeniach i uzyskać najbardziej

uproszczony wzór

ܬ

௄

=

ܮ

௠௔௫

߱

ś௥

ଶ

ߜ

(20)

Wzory (19) i (20) służą do obliczania momentu bezwładności koła zamachowego w sposób
przybliżony.

Zauważmy ze wzór (20) jest analogiczny do (10) z tym, że zamiast momentu

bezwładności całej maszyny wpisujemy moment bezwładności koła zamachowego. Oznacza

6

to ze moment maszyny jest pomijalnie mały w stosunku do zredukowanego momentu
bezwładności koła zamachowego, w przypadku użycia wzoru (20).

Mając dany moment bezwładności koła zamachowego należy wyznaczyć jego

wymiary rzeczywiste. Koło takie powinno mieć jak najwięcej masy skupionej na obrzeżach,
co spowoduje obniżenie masy całkowitej a zarazem zachowanie wymaganego momentu
bezwładności. Nie trzeba dodawać, iż niższa masa koła powoduje mniejsze straty energii na
jego obrót.



Literatura

- J. Felis, H. Jaworski, J. Cieślik „Teoria maszyn i mechanizmów. Część I analiza
mechanizmów”

- Z. Parszewski „Teoria maszyn i mechanizmów”