METODA ELEMENTÓW SKOŃCZONYCH
Przykład 1. Kratownica płaska – formalizm MES. Dane: A=15
× 10
-4
m
2
, E = 2.0
× 10
11
Pa
P=12 kN
1
3
2
4 m
3
m
4 m
4
1
5
2
4
3
2
4
6
7
8
1
3
5
V
A
V
B
H
A
Y
X
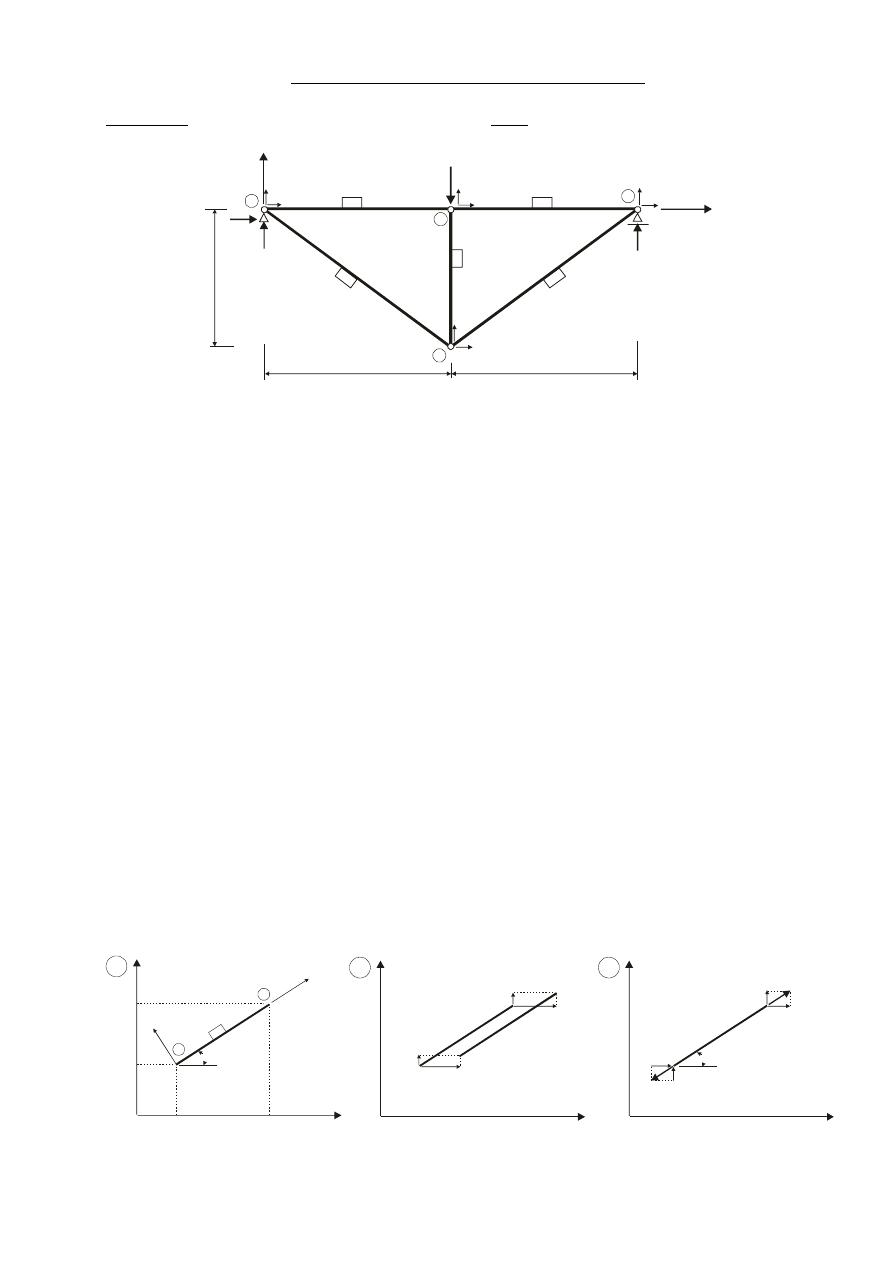
Rys.1.
1. Dyskretyzacja. W kratownicy podział jest oczywisty – pręt jest elementem, węzeł kratowy
węzłem w rozumieniu MES. Przy podziale na węzły i elementy w układzie globalnym X,Y
numery elementów oznaczono przez e (e=1,2,...5), numery węzłów przez i (i=1,...4);
5 elementów, 4 węzły. Węzły ponumerowano tak, aby znane stopnie swobody (nieruchome
równe 0) były na końcu wektora r. Jest to wygodne w obliczeniach ręcznych, niekoniecznie
przy analizie komputerowej. Dla dalszych potrzeb rozróżniamy prawoskrętny układ globalny
X,Y,Z oraz prawoskrętny lokalny x,y,z związany z elementem. Początek układu lokalnego
umieszczamy w węźle o niższym numerze, a zwroty osi z i Z powinny być zgodne.
Wektory węzłowych stopni swobody r i sił węzłowych R mają następującą postać:
−
=
=
=
=
=
=
A
A
B
4
4
3
3
2
2
1
1
8
7
6
5
4
3
2
1
V
H
V
0
0
0
12
0
0
v
0
u
0
v
u
v
u
v
u
r
r
r
r
r
r
r
r
R
r
2. Macierz sztywności elementu kratownicy płaskiej k
e
w globalnym układzie
współrzędnych z równania Q
e
= k
e
⋅q
e
V =-Ns
a
b
b
a
V =Ns
H =-Nc
H =Nc
N
N
Y
Y
Y
X
X
X
X
Y
u
u
v
v
Y
X
x
y
a
e
l
l
a
a
a
a
b
a
b
b
b
α
l
l
+∆
α
b
b
c
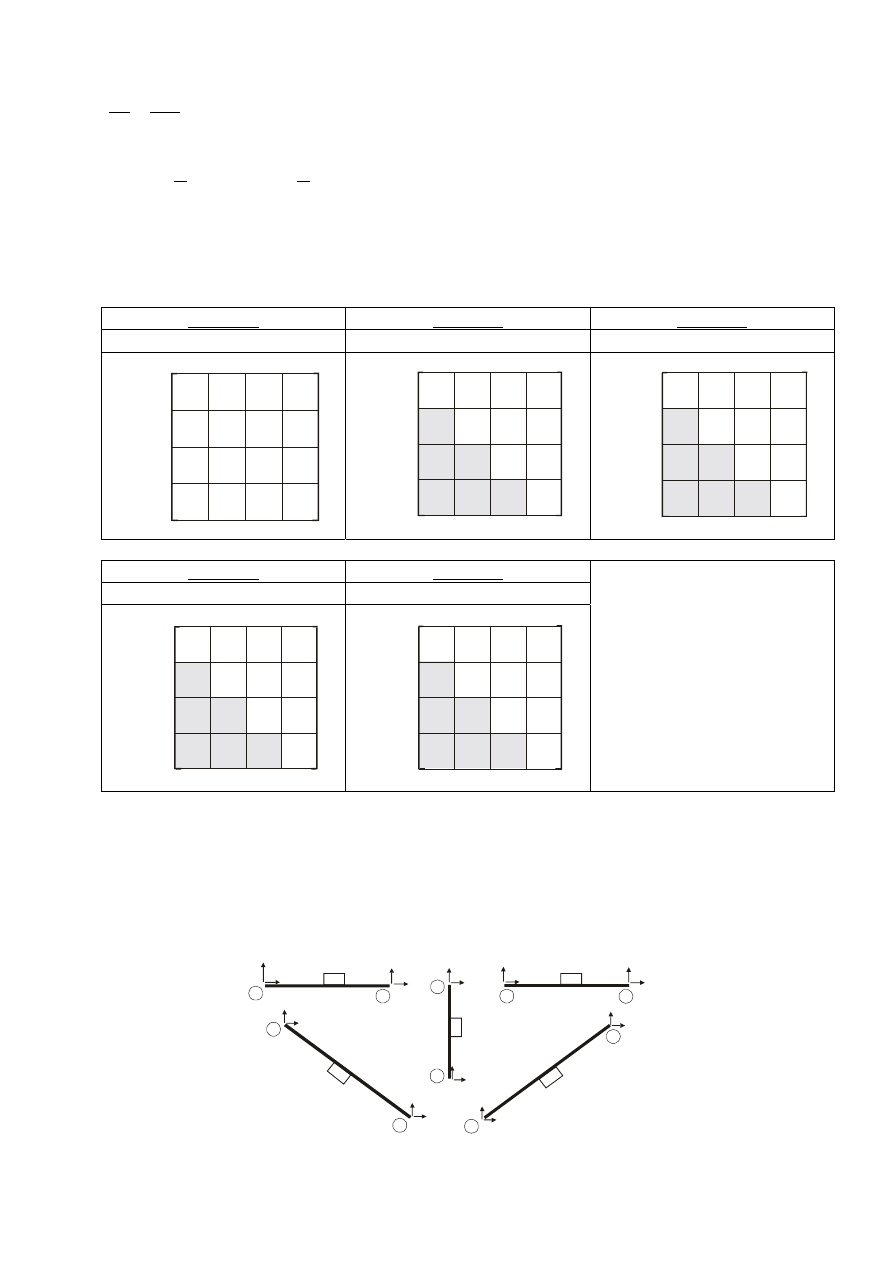
Rys.2.
1

Na rysunku 2.a przedstawiono typowy element o numerze e i dwóch węzłach. Węzeł o numerze
niższym oznaczono literą a , a o wyższym literą b .
Długość pręta
(
) (
)
2
2
a
b
a
b
X
X
Y
Y
−
+
−
=
l
(
)
(
)
.
1
sin
1
cos
a
b
a
b
Y
Y
l
s
X
X
l
c
−
=
=
−
=
=
α
α
Na rysunku 2.b pokazano przemieszczenia pręta określone przez przesuniecia końców mierzone w
globalnym układzie współrzędnych, tzn. wektor przemieszczeń węzłowych elementu e jest
postaci
=
b
b
a
a
e
v
u
v
u
q
Wydłużenie pręta obliczamy jako różnicę rzutów przesunięć końców na jego kierunek
(
) (
)
[
]
⋅
−
−
=
∆
−
+
−
=
∆
b
b
a
a
a
b
a
b
v
u
v
u
s
c
s
c
l
,
s
v
v
c
u
u
l
.
W elemencie jest stała siła podłużna N , której rzuty H
i
i V
i
, (i=a,b), w węzłach podano na
rysunku 2.c . Wektor sił węzłowych Q
e
odpowiadający wektorowi q
e
ma postać:
−
−
=
−
−
=
=
s
c
s
c
N
s
N
c
N
s
N
c
N
V
H
V
H
b
b
a
a
e
Q
Z prawa Hooke’a
l
l
EA
N
∆
=
zatem
[
]
e
e
s
c
s
c
s
c
s
c
l
EA
q
Q
⋅
−
−
⋅
−
−
=
z tego zapisu ostatecznie otrzymamy
c c
EA
l
k
e
=
c s
-c c -c s
s c
s s
-s c -s s
-c c -c s c c
c s
-s c -s s
s c
s s
2
Należy zauważyć, że w elemencie przyjęto stałą siłę N. Ponieważ N=A
⋅E⋅ε to ε=const i
0
dx
u
d
dx
d
2
2
=
=
ε
. Zatem u(x) = A
o
+A
1
x. Oznacza to, że w elemencie dokonano liniowej aproksymacji
pola przemieszczeń, które może być zapisane w postaci u(x)=N
1
(x)
∆
a
+N
2
(x)
∆
b
, gdzie
l
x
1
)
x
(
N
,
l
x
)
x
(
N
1
2
−
=
=
, a
∆
a
i
∆
b
są przesunięciami końców elementu wzdłuż osi pręta.
Macierze sztywności poszczególnych elementów są następujące:
element 1 element
3 element
4
cos
α=-1 ; sinα=0 ; l = 4 m ,
cos
α=-0,8 ; sinα=0,6 ; l = 5 m , cosα=0,8 ; sinα=0,6 ; l = 5 m ,
0,25
r
r
r
r
r
r
r
r
1
1
2
7
8
2
7
8
-0,25
0
0
0
0
-0,25
0,25
EA
k
1
=
0
0
0
0
0
0
0
0
r
r
r
r
r
r
r
r
3
3
4
7
8
4
7
8
0,128
s y
m
etr
i a
0,072
0,128 -0,096
-0,096 -0,128 0,096
EA
k
3
=
0,072 0,096 -0,072
r
r
r
r
r
r
r
r
3
3
4
5
6
4
5
6
0,128
s y
m
e tr
i a
0,072
0,128 0,096
0,096 -0,128 -0,096
EA
k
4
=
0,072 -0,096 -0,072
element 5 element
2
cos
α=0 ; sinα=-1 ; l = 3 m ,
cos
α=1 ; sinα=0 ; l = 4 m ,
Na bokach macierzy
szczególnych elementów
zapisano globalne stopnie
swobody odpowiadające
numerom kolumn i wierszy.
po
r
r
r
r
r
r
r
r
1
1
2
3
2
3
4
0
0
0
0
s y
m
e tr
i a
0,333
0
0
EA
k
5
=
0,333
0
-0,333
4
r
r
r
r
r
r
r
r
1
1
2
5
6
2
5
6
0,25
s y
m
e tr
i a
0
0
0
-0,25
0,25
EA
k
2
=
0
0
0
0
3. Macierz sztywności konstrukcji – „zszywanie” elementów: połączenia i równowaga.
Wykorzystujemy równania równowagi poszczególnych węzłów oraz zgodność przemieszczeń
w węzłach. Zgodność przemieszczeń zapewnia się przez przyjęcie globalnej numeracji stopni
swobody w każdym elemencie (np. dla elementu 5 u
1
=r
1
, v
1
=r
2
, u
2
=r
3
, v
2
=r
4
– patrz rysunek).
1
1
1
3
3
2
2
2
4
1
5
2
4
3
4
v = r
u = r
u = r
u = r
u = r
u = r
u = r
v = r
v = r
v = r
v = r
v = r
3
3
1
1
1
2
4
1
1
1
2
4
6
5
1
1
1
3
7
2
2
2
4
8
Rys.3.
3
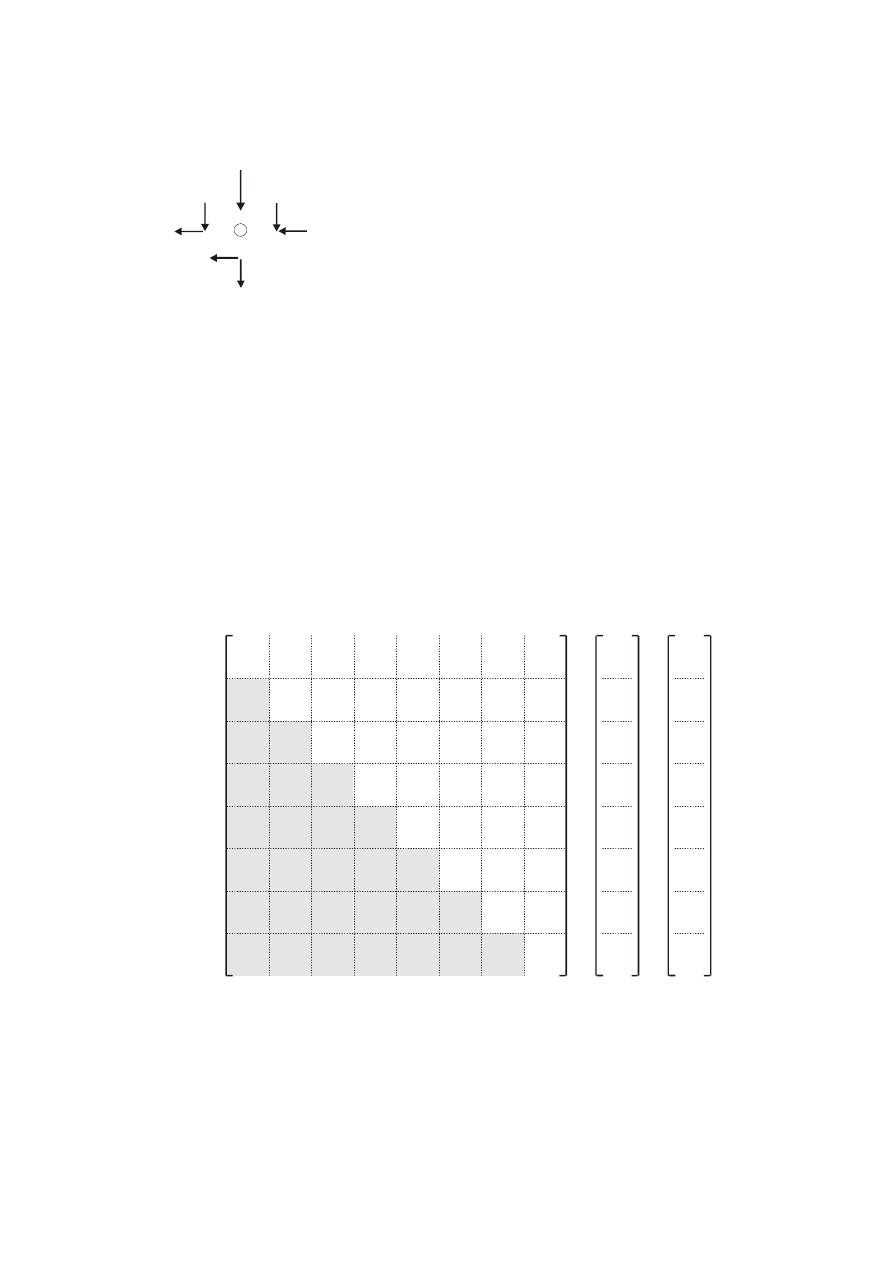
Przykładowo równowaga węzła 1 (dwa pierwsze równania równowagi, węzeł wspólny dla
elementów nr 1, 2 i 5):
12 kN
Q
Q
Q
Q
Q
Q
e=1
e=1
e=2
e=2
e=5
e=5
2
1
2
1
1
2
1
kN
12
Q
Q
Q
0
Y
0
Q
Q
Q
0
X
2
5
e
2
2
e
2
1
e
1
5
e
1
2
e
1
1
e
−
=
+
+
⇒
=
=
+
+
⇒
=
=
=
=
=
=
=
∑
∑
Występujące w równaniach siły węzłowe elementów wyrażamy za pomocą zależności Q
e
= k
e
⋅
q
e
wykorzystując warunki połączenia (zgodności przemieszczeń):
12
)
r
333
,
0
r
333
,
0
(
EA
:
2
równanie
)
r
333
,
0
r
333
,
0
(
EA
Q
,
0
Q
,
0
Q
0
)
r
25
,
0
r
25
,
0
r
5
,
0
(
EA
:
1
równanie
0
Q
,
)
r
25
,
0
r
25
,
0
(
EA
Q
,
)
r
25
,
0
r
25
,
0
(
EA
Q
4
2
4
2
2
5
e
2
2
e
2
1
e
7
5
1
1
5
e
5
1
1
2
e
7
1
1
1
e
−
=
−
−
=
=
=
=
−
−
=
−
=
−
=
=
=
=
=
=
=
W podobny sposób można uzyskać pozostałe równania. Po zbudowaniu układu równań tj.
macierzy sztywności konstrukcji oprócz macierzy sztywności poszczególnych elementów w
układzie globalnym potrzebne są także globalne numery wierszy i kolumn wynikające ze sposobu
połączeń. Budowa (agregacja) macierzy sztywności konstrukcji polega na sumowaniu wyrazów o
tych samych numerach globalnych wierszy i kolumn – jest to tzw. dodawanie z alokacją.
r
0
-12
0
0
0
V
A
H
A
V
B
r
r
r
r
r
r
r
=
1
2
3
4
5
6
7
8
k
k
k
k
k
k
k
1
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
+
+
+
+
+
+
+
11
22
24
13
31
31
13
11
12
13
23
34
44
34
44
24
23
24
14
13
14
22
33
33
11
11
12
44
22
33
33
1
5
5
2
1
2
1
3
3
4
4
4
3
3
4
4
3
3
4
3
3
3
2
1
2
4
4
5
4
4
3
s y
m
e tr
i a
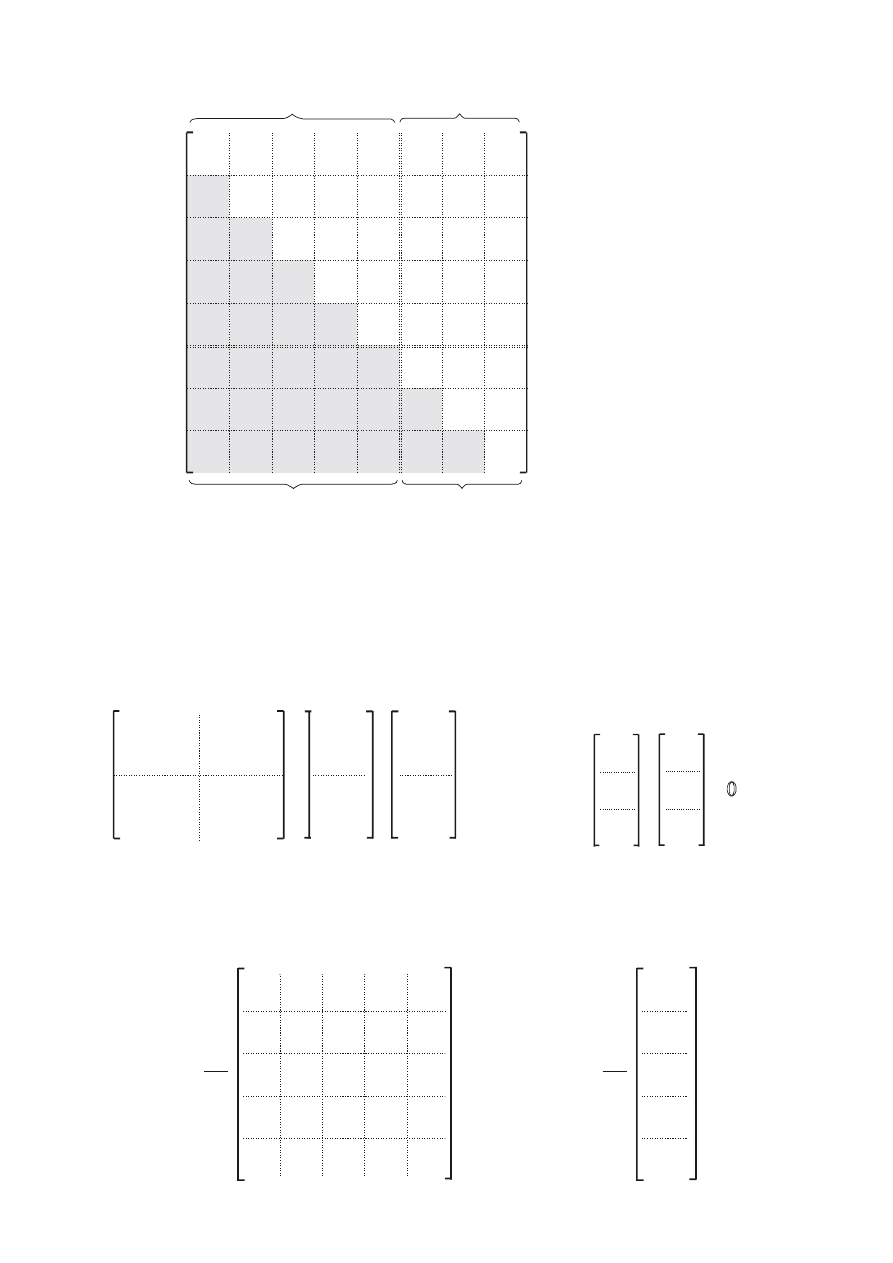
Zatem macierz sztywności konstrukcji ma postać ( w macierzy elementy zerowe opuszczono):
4
sy
m
e tr
i a
K=
K
K
K
EA
0,5
0,333
-0,333
0,256
-0,128 -0,096
0,096
-0,096 -0,072 0,096 -0,072
-0,128
0,477
0,378 0,096
0,072
0,378 -0,096
0,072
-0,25
-0,25
K
11
21
22
12
K
⋅ r = R
4. Rozwiązanie równań równowagi – uwzględnianie warunków brzegowych.
Rozwiązanie jest możliwe po uwzględnieniu sposobu podparcia konstrukcji. Równanie (1)
zapiszemy w postaci blokowej rozróżniając stałe (nieruchome) stopnie swobody (r
6
= r
7
= r
8
) oraz
ruchome, nieznane stopnie swobody (pozostałe).
K
K
K
K
r
R
r
R
11
(5 x 5)
(3 x 5)
(3 x 3)
x
=
(3 x 1)
(5 x 3)
(5 x 3)
21
22
12
1
1
0
0
, gdzie
r
0
nieruchome stopnie swobody:
r
r
r
0
0
0
r =
=
=
6
7
8
0
=
+
=
⇒
=
⇒
=
+
−
−
.
reakcje
obliczamy
swobody
stopni
ych
hom
ruc
obliczeniu
po
.
tzn
R
r
K
r
K
)
R
K
(
K
R
R
K
r
0
0
22
1
21
1
1
11
21
0
1
1
11
1
1
0
12
1
11
R
r
K
r
K
=
4
4
4
4
4
2.667
2.667
2.667 10.5
10.5
10.5
5.333
5.333
5.333
5.333
8
13.503
2.667
2
2
2.667
2.667
2.667
2.667
5.906
K
EA
1
11
-1
=
=
-32
-64
-162.036
-32
-126
r
r
r
r
r
r
K R
EA
1
1
1
2
3
4
5
1
-1
5
=
=
=
−
6
10
6
V
H
V
r
K
R
:
akcje
Re
15
A
A
B
1
21
0
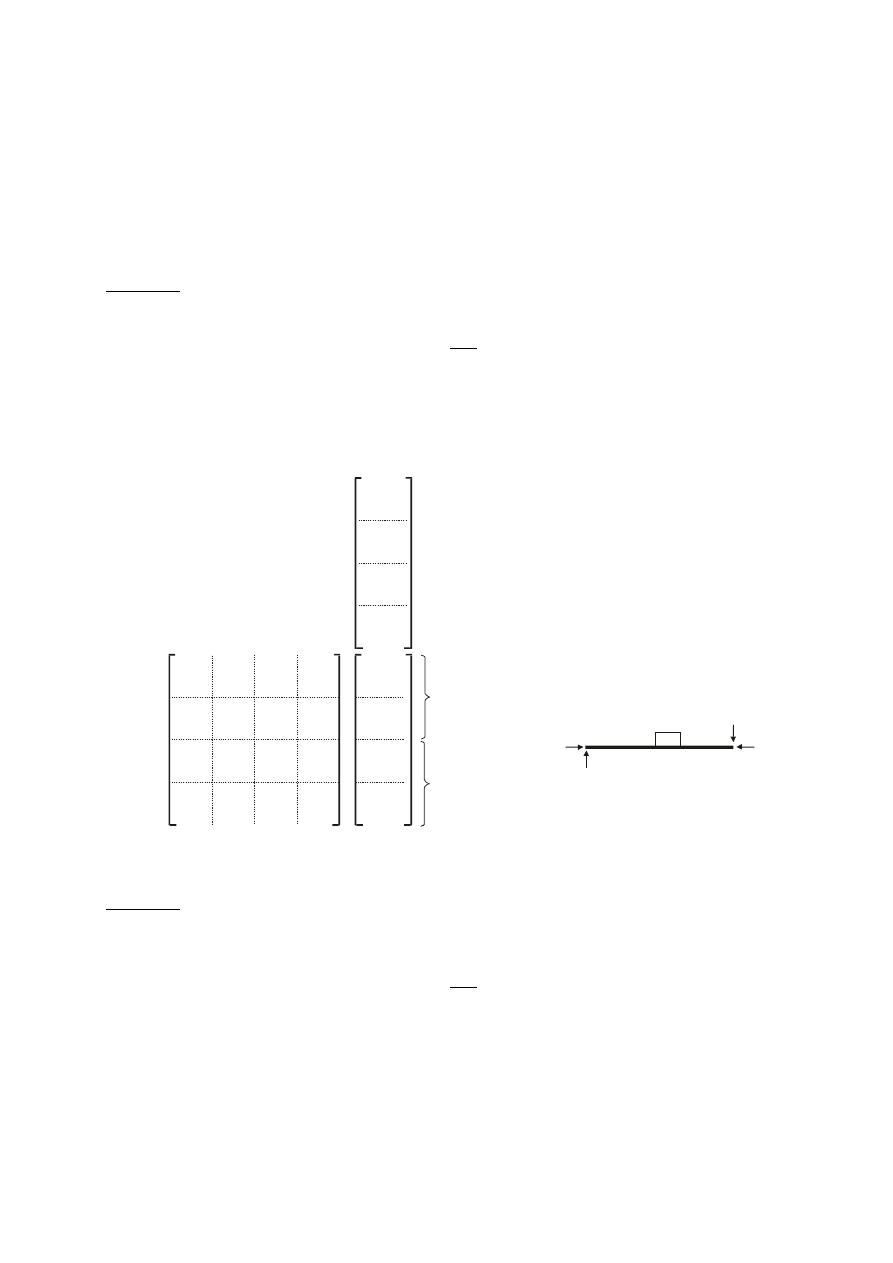
5. Obliczanie sił przekrojowych.
Obliczamy je z zależności Q
e
= k
e
q
e .
Element 1
−
−
=
=
0
0
036
.
162
32
EA
1
r
r
r
r
8
7
2
1
1
q
Ponieważ Q
1
= k
1
q
1
, możemy zapisać i wyliczyć
0,25
-0,25
0
0
0
0
-0,25
0,25
0
0
0
0
0
0
0
0
-8
-8
-32
0
węzeł
początkowy
węzeł
końcowy
-162,036
0
0
0
1
0
8
8
początk.
końcowy
0
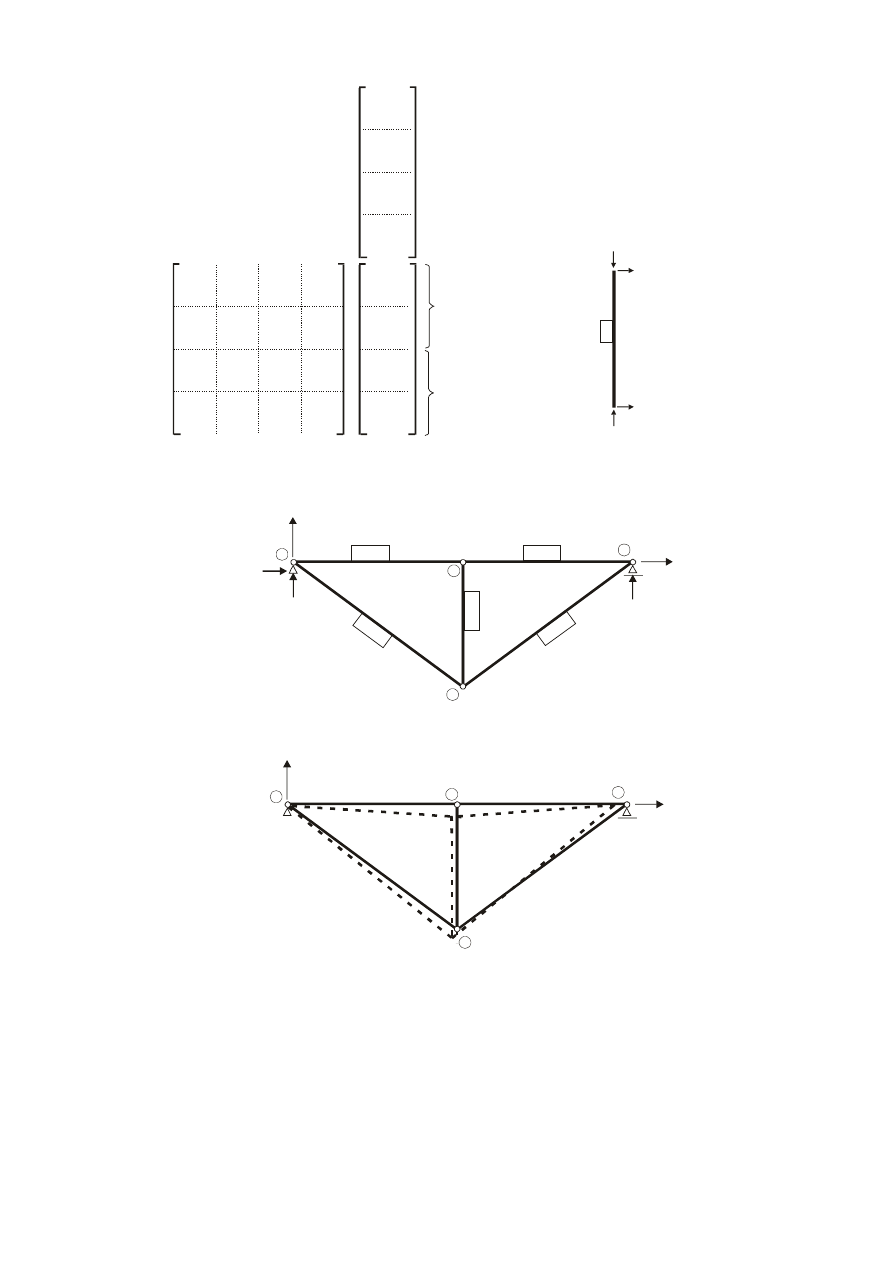
Element 5
Ponieważ Q
5
= k
5
q
5
, możemy zapisać i wyliczyć
−
−
−
−
=
=
126
32
036
.
162
32
EA
1
r
r
r
r
4
3
2
1
5
q
6
0
0
0
0
0
0
0
0
0
0
0.333
-0.333
-0.333
0.333
0
0
0
-32
-12.013
węzeł
początkowy
węzeł
końcowy
-162,036
0
12.013
-126
-32
5
0
12,0
12,0
początk.
końcowy
0
Ostatecznie wykres sił przekrojowych (rys. 4a) oraz przemieszczeń (rys. 4b) są następujące:
1
3
2
4
V = 6 kN
A
-8 kN
-8 kN
V = 6 kN
B
H = 0
A
Y
X
10
kN
-1
2 k
N
10 k
N
Rys.4a.
1
3
2
4
Y
X
Rys. 4b.
7
Wyszukiwarka
Podobne podstrony:
Sprawozdanie MES 4 kratownica
KRATOW1, Sprawozdanie z mexhaniki (MES)
Lab 8 Kratownica MES
Robimy elementy belkowe, Studia Politechnika Poznańska, Semestr VI, Systemy MES, Lab-Projekt Wojtek,
Autodesk Robot Structural Analysis Professional 2010 Projekt maszt kratownica przestrzenna Wyniki
Kratownica trzykrotnie statycznie niewyznaczalna
MES 02
mes rama
K8 kratownice K4
program zad1
kratownica belka 57
MES, Polibuda MBM PWR 2012-2016, Sem. V, MES, koło
zad1, Informatyka i Ekonometria 3 rok, Ekonometria, sliwka
1 M2 StepnowskaA StepnowskaM ZAD1
Sprawozdanie MES
Cegła kratówka i?ny 09
więcej podobnych podstron