
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
Z
ESTAW PRZYGOTOWANY PRZEZ SERWIS
WWW
.
ZADANIA
.
INFO
POZIOM PODSTAWOWY
15
MARCA
2014
C
ZAS PRACY
: 170
MINUT
1

✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Zadania zamkni˛ete
Z
ADANIE
1
(1
PKT
)
Liczba 43256232a2 jest podzielna przez 4 je ˙zeli
A) a
=
0
B) a
=
2
C) a
=
3
D) a
=
4
Z
ADANIE
2
(1
PKT
)
Dodatnia liczba x stanowi 30% liczby y. Wówczas
A) y
=
17
10
x
B) y
=
10
3
x
C) y
=
7
10
x
D) y
=
13
10
x
Z
ADANIE
3
(1
PKT
)
Liczba
8
3
·
16
√
8
jest równa
A) 2
11
√
2
B) 2
12
√
2
C) 2
8
√
2
D) 8
5
√
2
Z
ADANIE
4
(1
PKT
)
Rozwi ˛azaniem układu równa ´n
(21x
−
14y
= −
28
6y
+
9x
=
48
jest para liczb
A) x
= −
3 i y
=
5
B) x
= −
3 i y
=
6
C) x
=
5 i y
=
2
D) x
=
2 i y
=
5
Z
ADANIE
5
(1
PKT
)
Liczba
(−
2
)
jest pierwiastkiem równania 3mx
=
4
−
x
. Wtedy
A) m
= −
1
B) m
=
1
C) m
=
2
D) m
= −
2
Z
ADANIE
6
(1
PKT
)
Wyra ˙zenie W
=
√
x
2
−
4x
+
4
−
√
4x
2
dla x > 2 przyjmuje posta´c
A) x
+
2
B)
−
3x
+
2
C)
−
x
−
2
D) x
−
2
Z
ADANIE
7
(1
PKT
)
Prosta y
=
ax
−
2 jest równoległa do prostej y
=
2x
−
ax
. Wtedy
A) a
= −
1
B) a
=
1
3
C) a
=
1
D) a
=
1
2
2
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
8
(1
PKT
)
Do zbioru rozwi ˛aza ´n nierówno´sci
(
x
+
√
5
−
1
)(
x
+
√
5
+
1
) <
0 nale ˙zy liczba
A) 0
B)
−
3
C)
−
1
D) 3
Z
ADANIE
9
(1
PKT
)
K ˛at α jest k ˛atem ostrym oraz tg α
=
1
4
. Zatem
A) cos α
=
4
√
17
B) sin α
=
4
√
17
C) sin α
=
1
17
D) cos α
=
1
√
17
Z
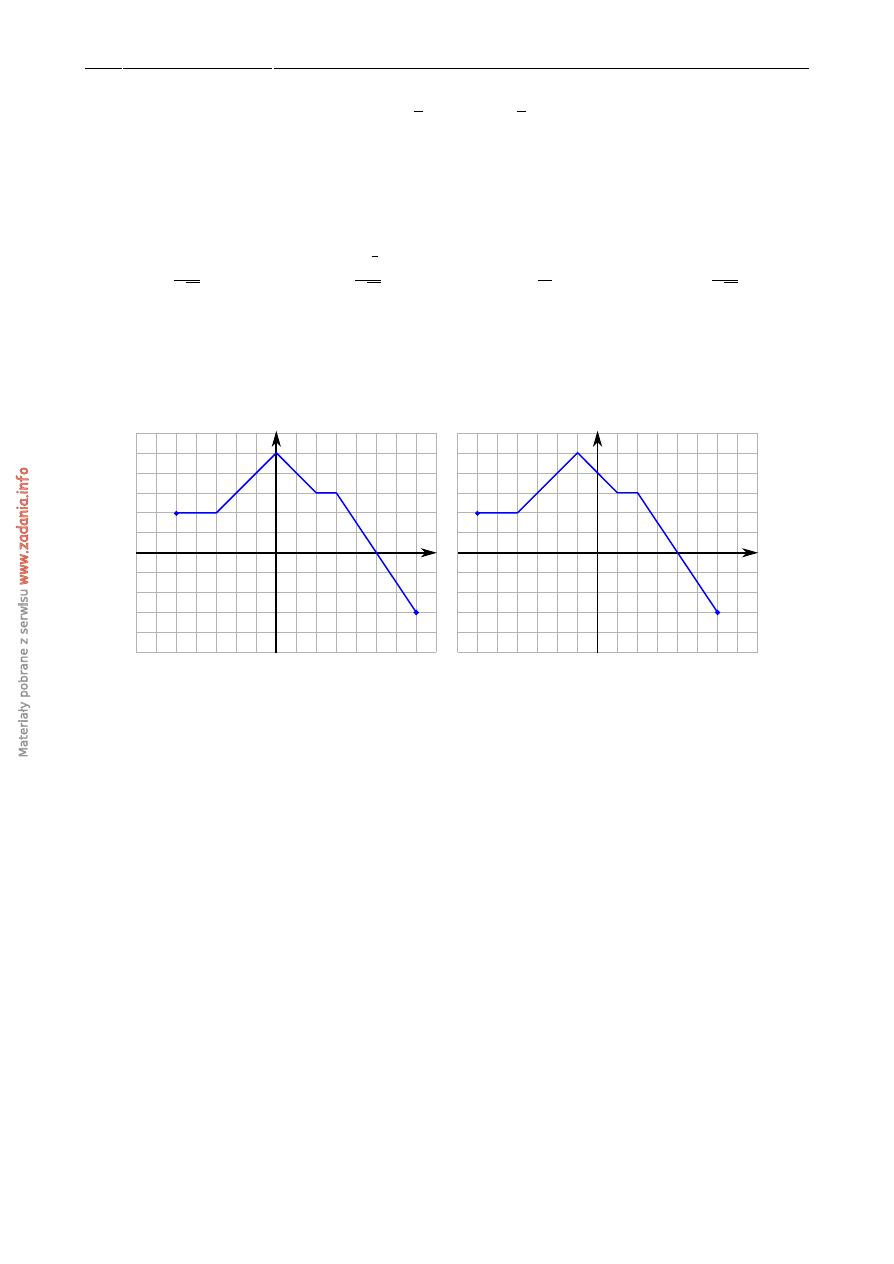
ADANIE
10
(1
PKT
)
Na poni ˙zszych rysunkach przedstawiono wykresy funkcji f i g.
x
y
1
2
3
4
5
6
1
2
3
4
5
-1
-1
-2
-2
-3
-4
-5
-6
-3
-4
7
f(x)
x
y
1
2
3
4
5
6
1
2
3
4
5
-1
-1
-2
-2
-3
-4
-5
-6
-3
-4
7
g(x)
Funkcja g jest okre´slona wzorem
A) g
(
x
) =
f
(
x
−
1
)
B) g
(
x
) =
f
(
x
) −
1
C) g
(
x
) =
f
(
x
+
1
)
D) g
(
x
) =
f
(
x
) +
1
Z
ADANIE
11
(1
PKT
)
Wielomian W
(
x
) = (
x
2
−
3
)
3
jest równy wielomianowi
A) x
6
−
3x
4
+
9x
2
−
27
B) x
6
+
9x
4
−
27x
2
−
27
C) x
6
−
27
D) x
6
−
9x
4
+
27x
2
−
27
Z
ADANIE
12
(1
PKT
)
Dany jest ci ˛ag
(
a
n
)
o wyrazie ogólnym a
n
=
n
−
n
2
, gdzie n > 1. Wówczas
A) a
n
+
1
=
n
2
−
n
B) a
n
+
1
=
n
+
1
−
n
2
C) a
n
+
1
=
n
−
n
2
D) a
n
+
1
= −
n
2
−
n
3

✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
13
(1
PKT
)
Prostok ˛at ABCD o przek ˛atnej długo´sci
√
2 jest podobny do prostok ˛ata o bokach długo´sci 1
i 7. Obwód prostok ˛ata ABCD jest równy
A)
16
5
B)
16
25
C) 80
D) 16
Z
ADANIE
14
(1
PKT
)
Ci ˛agiem geometrycznym jest ci ˛ag okre´slony wzorem
A) a
n
=
n
4
−
1
B) a
n
= (−
1
)
n
C) a
n
=
1
n
D) a
n
=
1
−
3n
Z
ADANIE
15
(1
PKT
)
Ile jest wszystkich liczb naturalnych czterocyfrowych podzielnych przez 5 ?
A) 2000
B) 1800
C) 1000
D) 900
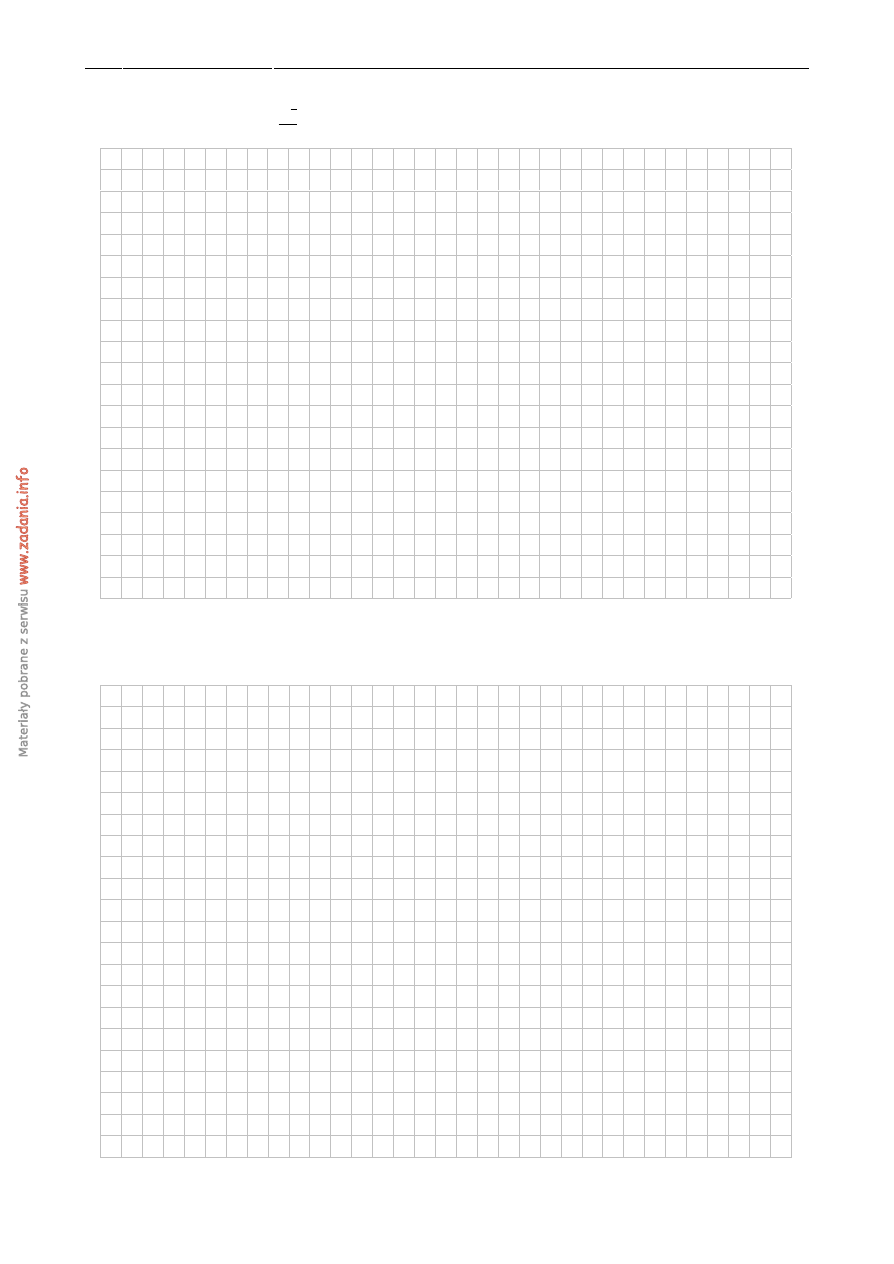
Z
ADANIE
16
(1
PKT
)
Dany jest okr ˛ag o ´srodku w punkcie O. Prosta k jest styczna do okr˛egu w punkcie A.
O
α
k
20
o
120
o
A
Miara k ˛ata α jest równa
A) 40
◦
B) 30
◦
C) 25
◦
D) 20
◦
Z
ADANIE
17
(1
PKT
)
Funkcja f
(
x
) =
3x
(
x
3
+
5
)(
2
−
x
)(
x
+
1
)
ma dokładnie
A) 1 pierwiastek
B) 2 pierwiastki
C) 3 pierwiastki
D) 4 pierwiastki
Z
ADANIE
18
(1
PKT
)
Obwód równoległoboku ABCD o wierzchołkach A
= (
1,
−
1
)
, B
= (
7, 3
)
, C
= (
9, 6
)
, D
= (
3,
2
)
jest równy
A) 3
√
13
B) 6
√
13
C) 8
√
13
D) 4
√
13
4

✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
19
(1
PKT
)
Liczba kraw˛edzi graniastosłupa jest o 8 wi˛eksza od liczby jego ´scian. Ile wierzchołków ma
ten graniastosłup?
A) 5
B) 15
C) 10
D) 16
Z
ADANIE
20
(1
PKT
)
Pi ˛aty wyraz ci ˛agu arytmetycznego jest równy
−
12, a ró ˙znica tego ci ˛agu jest równa
(−
5
)
.
Drugi wyraz tego ci ˛agu jest równy
A) 8
B)
−
7
C)
−
2
D) 3
Z
ADANIE
21
(1
PKT
)
Pole koła ograniczonego okr˛egiem x
2
+
y
2
+
2x
−
6y
+
5
=
0 jest równe
A)
√
5
B)
√
5π
C) 25π
D) 5π
Z
ADANIE
22
(1
PKT
)
Mediana uporz ˛adkowanego niemalej ˛aco zestawu sze´sciu liczb: 1, 2, 4, x, 7, 8 jest równa 5.
Wtedy
A) x
=
4
B) x
=
5
C) x
=
6
D) x
=
7
Z
ADANIE
23
(1
PKT
)
Rzucamy dwa razy symetryczn ˛a sze´scienn ˛a kostk ˛a do gry. Prawdopodobie ´nstwo dwukrot-
nego otrzymania liczby oczek ró ˙znej od 5 jest równe
A)
1
6
B)
5
18
C)
35
36
D)
25
36
Z
ADANIE
24
(1
PKT
)
Obj˛eto´s´c sto ˙zka o wysoko´sci h i promieniu podstawy cztery razy mniejszym od wysoko´sci
jest równa
A)
1
24
π
h
3
B)
1
48
π
h
3
C)
1
12
π
h
3
D)
1
64
π
h
3
Z
ADANIE
25
(1
PKT
)
Liczba log
3
6
1
2
−
log
3
√
8
+
log
3
2 jest równa
A)
√
3
B)
1
2
C) log
3
2
D) log
3
6
5
Z
ADANIE
26
(2
PKT
)
K ˛at α jest ostry i sin α
=
√
2
2
. Oblicz warto´s´c wyra ˙zenia 3 cos
2
α
−
2 sin
2
α
.
Z
ADANIE
27
(2
PKT
)
Rozwi ˛a˙z równanie x
5
−
7x
4
+
3x
−
21
=
0.
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
6
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
28
(2
PKT
)
Udowodnij, ˙ze je ˙zeli liczby niezerowe a, b, c spełniaj ˛a warunek a
+
b
+
c
=
0 to
a
2bc
+
b
2ca
+
c
2ab
+
1
c
+
1
b
+
1
a
=
0.
7

✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
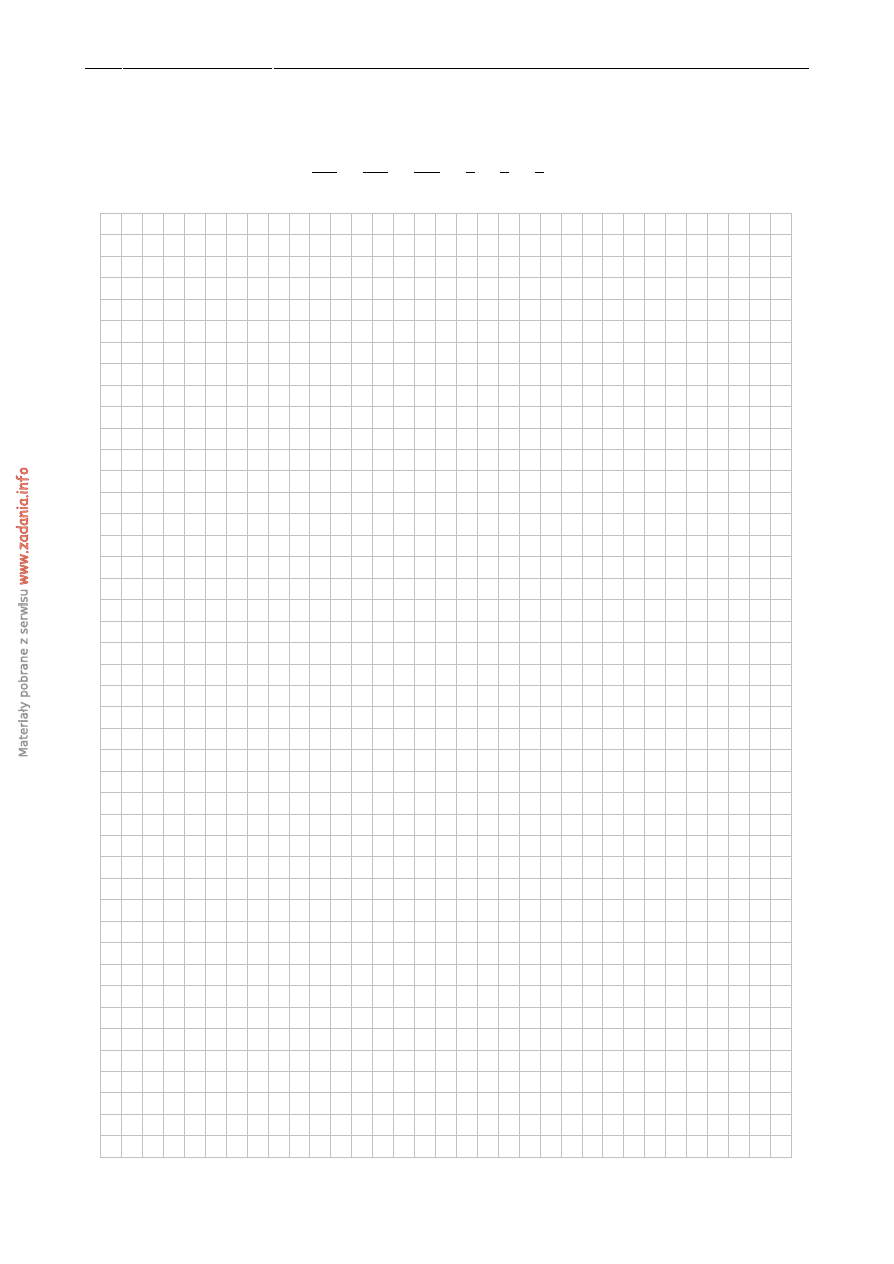
ADANIE
29
(2
PKT
)
Trójk ˛aty ABC i CDE s ˛a równoramienne i prostok ˛atne. Punkty A, C i E le ˙z ˛a na jednej prostej,
a punkty K, L i M s ˛a ´srodkami odcinków AC, CE i BD (zobacz rysunek). Wyka ˙z, ˙ze
|
MK
| =
|
ML
|
.
A
E
D
M
B
K
C
L
8
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
30
(2
PKT
)
Odcinek EF ł ˛acz ˛acy ´srodki dwóch dłu ˙zszych boków prostok ˛ata ABCD dzieli go na dwa
kwadraty, przy czym przek ˛atna prostok ˛ata jest o 3 dłu ˙zsza od przek ˛atnej kwadratu. Oblicz
pole prostok ˛ata ABCD.
A
B
C
D
E
F
9
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
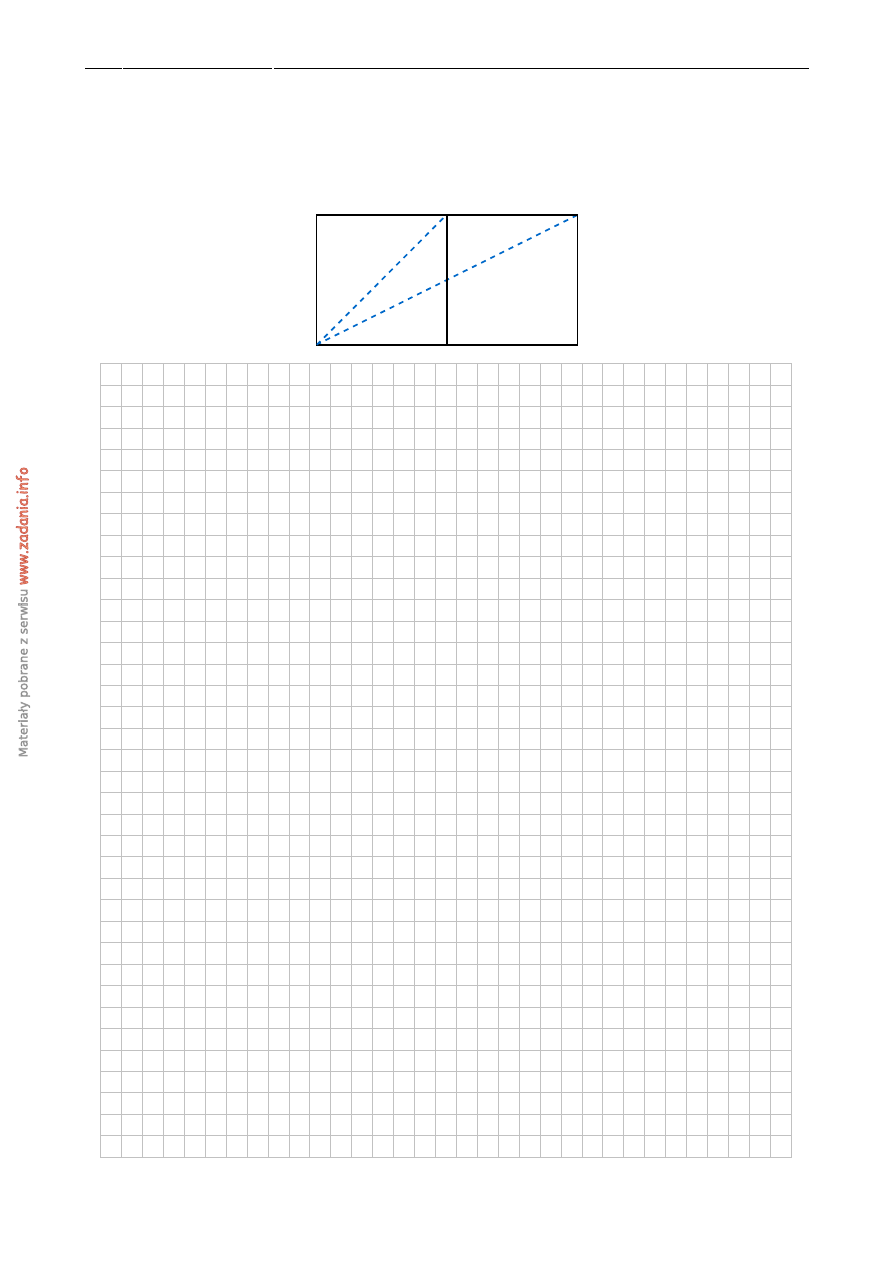
ADANIE
31
(2
PKT
)
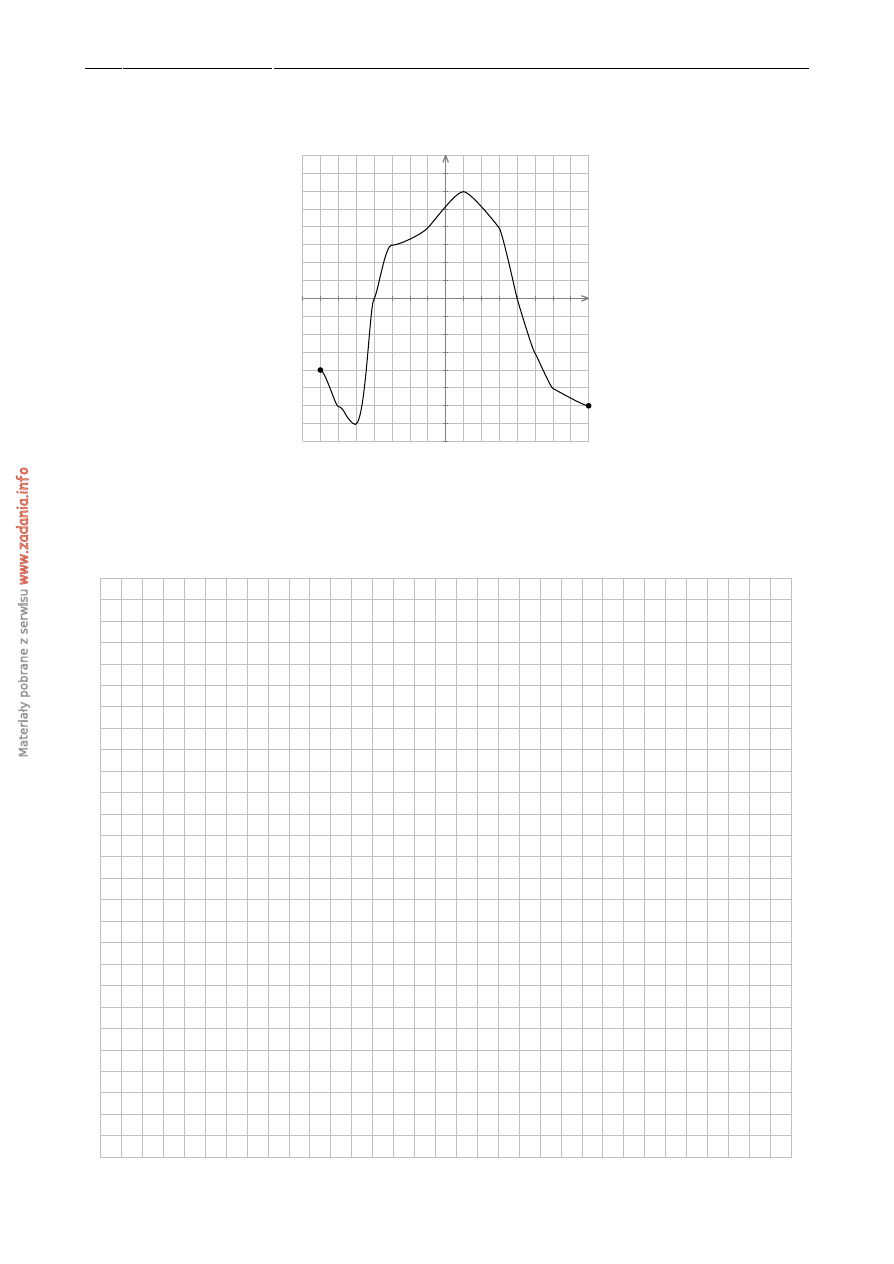
Na rysunku przedstawiony jest wykres funkcji f
(
x
)
okre´slonej dla x
∈ h−
7, 8
i
.
-5
-1
+3
+5
x
-5
-1
+1
+5
y
-6
-7
-4 -3
-2
+1 +2
+4
+6 +7 +8
+2
+3
+4
+6
+7
-2
-3
-4
-6
-7
Odczytaj z wykresu i zapisz:
a) najmniejsz ˛a warto´s´c funkcji f ,
b) zbiór rozwi ˛aza ´n nierówno´sci f
(
x
) <
0.
10
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
32
(4
PKT
)
Oblicz obj˛eto´s´c i pole powierzchni bocznej ostrosłupa prawidłowego sze´sciok ˛atnego o kra-
w˛edzi podstawy 2 cm i kraw˛edzi bocznej 6 cm.
11
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
33
(4
PKT
)
W pewnej szkole 47% uczniów ucz˛eszcza na kółko plastyczne, a 65% uczniów ucz˛eszcza na
kółko muzyczne. Wiadomo ponadto, ˙ze 30% uczniów ucz˛eszcza na obydwa kółka. Oblicz
prawdopodobie ´nstwo, ˙ze losowy wybrany ucze ´n tej szkoły nie ucz˛eszcza na ˙zadne z tych
kółek.
12
✇✇✇✳③❛❞❛♥✐❛✳✐♥❢♦ – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´N Z
M
ATEMATYKI
Z
ADANIE
34
(5
PKT
)
Wierzchołki trapezu ABCD maj ˛a współrz˛edne: A
= (−
1, 7
)
, B
= (−
9,
−
1
)
, C
= (−
1,
−
2
)
,
D
= (
3, 2
)
. Napisz równanie okr˛egu, który jest styczny do podstawy AB tego trapezu, a jego
´srodek jest punktem przeci˛ecia si˛e przek ˛atnych trapezu ABCD.
13
Wyszukiwarka
Podobne podstrony:
matura probna 2014 3 id 288983 Nieznany
arkusz i odpowiedzi matura probna biologia rozszerzona operon 2013 2014
Lubelska Matura próbna Luty 2014
Lubelska Matura probna Luty 2014 odp id 273537
Lubelska Matura próbna Luty 2014 odp
matura probna biologia 2014 oke
arkusz i odpowiedzi matura probna biologia rozszerzona operon 2013 2014
MATURA PRÓBNA Z MATEMATYKI 13
2015 matura probna JEZYK POLSKI Nieznany (2)
2015 matura próbna JĘZYK POLSKI poziom rozszerzony ARKUSZ
matura probna oke poznan styczen 2011 rozszerzony R id 7
matura próbna 05
matura probna oke poznan styczen 2011 podstawowy R id 77
Powtórka przed maturą próbną, WOS - matura, Matura 2015
matura próbna 2006, dokumenty, chemia
2015 matura próbna JĘZYK POLSKI poziom rozszerzony ODPOWIEDZI
matura zamkor 2014 odpowiedzi
więcej podobnych podstron