Logika Dla Prawników

Rozdział I: Zagadnienia wstępne

Starożytność
Zenon z Elei:

-

Twórca dialektyki(poszukiwał prawdy, wykorzystując argumenty
słowne).

Sokrates

-

Model tworzenia definicji

Platon:

-

Twórca rozumowania dedukcyjnego

Arystoteles:

-

Zasada sprzec

zności: „dwa zdania względem siebie sprzeczne

nie mogą być równocześnie prawdziwe”

-

Zasada wyłączonego środka: „ Z dwóch zdań sprzecznych
jedno musi być prawdziwe”

Porfejusz

-

Tzw. Drzewo porfejusza

Logika stoicka

(prekursorem był Chryzypem z Soloi) zajmowała się wartością logiczną zdań oraz

spójnikami.
Megarejczycy

zajmowali się paradoksami, czyli zdaniami wewnętrznie sprzecznymi(„czy prawdę mówi, kto

mówi, że to, co mówi, jest fałszem”).

Średniowiecze
Duns Szkot:

-

Prawo „Dunsa Szkota” (właściwości implikacji)

William kocham:

-

Początki twierdzeń o rachunku zdań

-

Problemy wynikania logicznego

Nowożytność

Piotr Ramus:

-

Krytyka Arystotelesa

-

Wprowadza nazwy jednostkowe

-

Podział logiki (na kategorie odnoszące się min. do definicji,
klasyfikacji, metody, sądów )

Kartezjusz:

-

Rozprawa o metodzie:

-

Unikanie

pochopności w wnioskowaniu, że coś jest prawdą lub nie

-

Dzielić każde zagadnienie na N podgrup, żeby rozwiązać trudność

-

Przechodzić stopniowo od rzeczy najłatwiejszych do trudniejszych

-

Wszystko

dokładnie sprawdzać.

Gottfried Wilhelm Leibniz:

-

Postawy

rachunku zdań

-

Definicja

relacji tożsamości

August de Morgen:

-

Prawo negacji i koniunkcji oraz prawo negacji alternatywy

-

Wkład w rozwój relacji

Georgie Bbole:

-

Logika jako

działem matematyki generalizacja specjalizacja i

ne

gacja = dodawanie, mnożenie i odejmowanie logiczne.

William Stanley Jevens:

-

Logika

– nauka o myśleniu

-

Podział logiki na dział o terminach, zdaniach sylogizmach i
metodzie

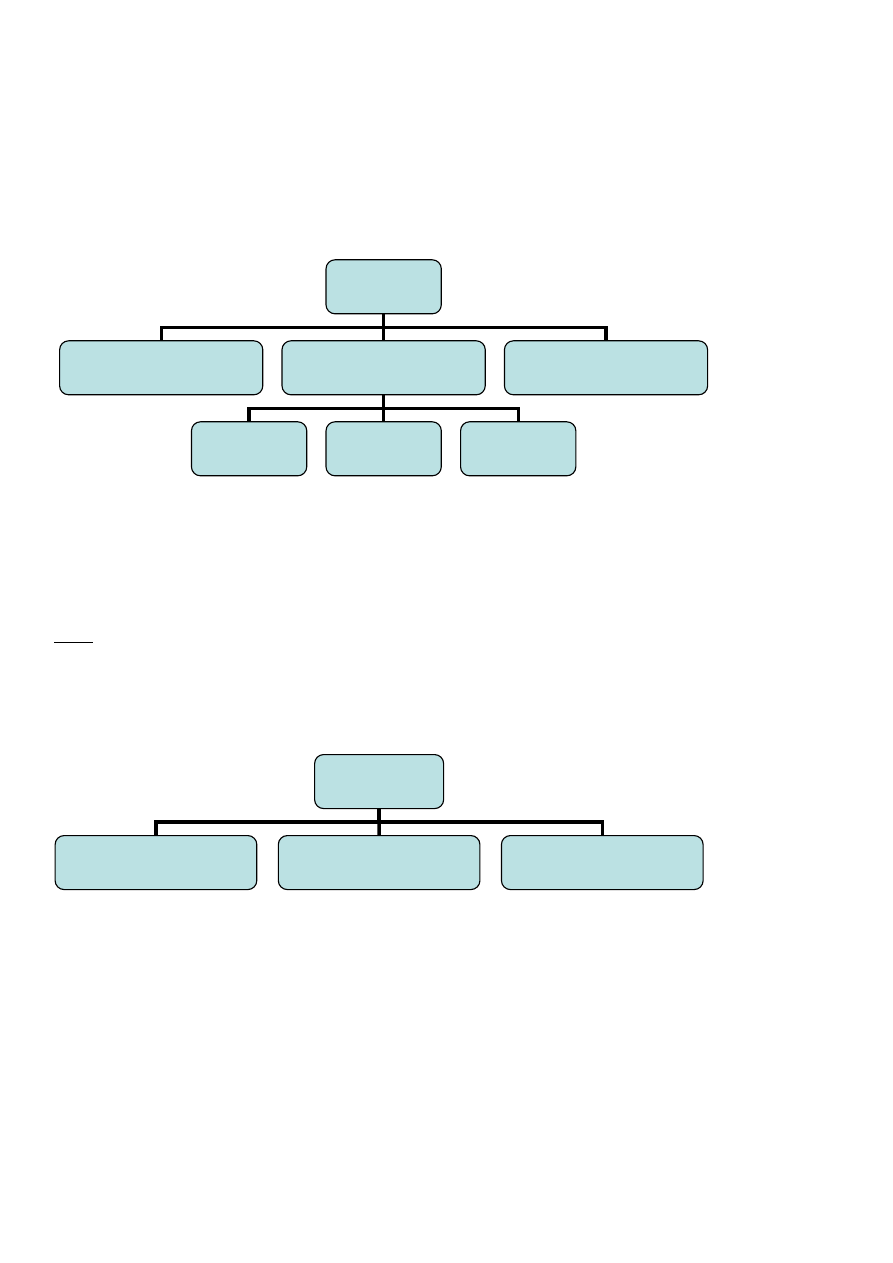
2

Gottlob Frege:

-

Funkcja

prawdziwościowa

-

System aksjomatyczny

-

Reguła odrywania

-

Twórca kwantyfikatorów

Jan Łukasiewicz:

-

Logika

trójwartościowa („0”, „1/2”, „1”)

Rozdział II: Znak, Język, Kategorie Syntaktyczne


Znak

Znak

– stan rzeczy spowodowany przez człowieka, który w danej sytuacji przekazuje jakąś treść(np.

podczas wojny biała szmata na kiju oznacza poddanie się, a podczas pokoju nic)

Znakami są np.

-

Znaki drogowe

-

Słowa (parasolka, umbrella, Schirm itd.)

-

Itp.

Znakami nie są:
Oznaka (symptom) -

powstaje samoistnie i też kieruje człowieka do określonych wniosków(woda na

ulicy = padał deszcz, spaliny = jechał samochód itp.)
Znaki ikoniczne

– przypominające obiekt opisywany (np. fotografia).

Logika

Logika formalna

Ogólna metodologia nauk

Semiotyka

Syntetyka

Semantyka

Pragmatyka

Znak

Element oznaczający(flaga)

Element

oznaczany(poddanie)

Funkcja znakotwórcza

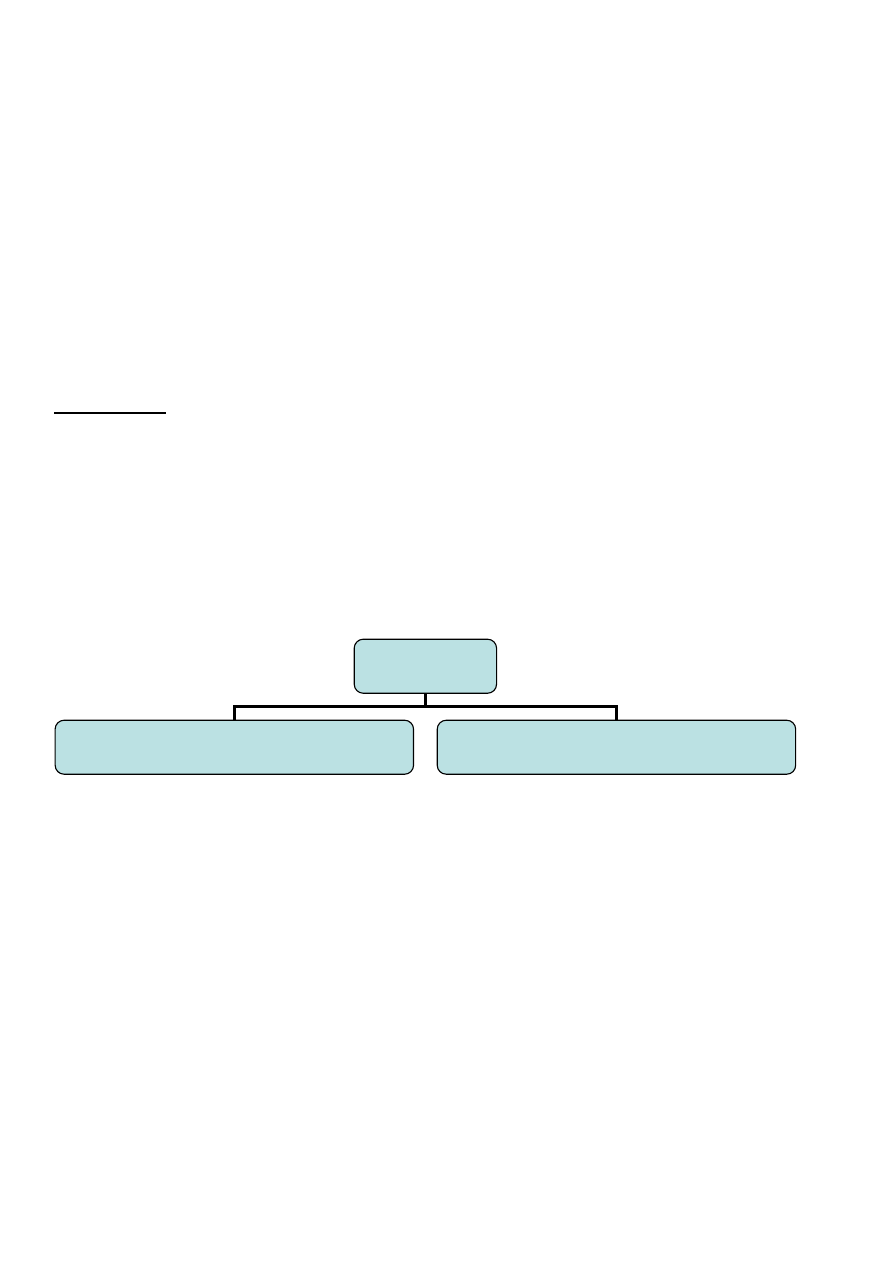
3

Wyraz

– Znak słowny stanowiący całość(np. logika długopis)

Wyrażenie – Sensowne zestawienie wyrazów( np. Uniwersytet Warszawski, piotr pije sok jabłkowy).

Wypowiedź może pełnić różne funkcje:

-

Funkcje opisową – gdy opisujemy rzeczywistość(np. UW mieści się
w Warszawie)

-

Funkcje ekspresywna

– gdy wyrażamy przeżycia uczucia(np.

Cholera! Kurwa

! O Boże! Itp.)

-

Funkcja sugestywna

– gdy zwrot stanowi bodziec do zachowania

się (np. Obierz ziemniaki! W tył zwrot! Itp.)

-

Funkcja performatywna

– Gdy wyrażenie niesie treść czysto

umowną wybiegającą poza zwykłe znaczenie czyt. Tylko w ściśle
określonych okolicznościach(np. ustanowienie wyroku przez sąd,
gdyby zwykły człowiek powiedział „jest winny” nie miałoby to
większego znaczenia lecz gdy orzeka to sąd wiąże się z pewnymi
konsekwencjami)nie jest ona prawdziwa albo fałszywa tylko ważna i
nieważna.

Pojęcia języka
Idiom

– specyficzne dla danego języka wyrażenie(np. płacić z góry)

Homonim

– wyraz mający wiele znaczeń (zamek)

Synonim

– wyrażenie lub wyraz którym w danym języku przypisano jednakowe znaczenia(bogacz =

krezus)

Semantyka

– powiązania między rzeczywistością wyrażeniem

Syntaktyka

– powiązania między wyrażeniami

Pragmatyka

– funkcja wypowiedzi w procesie porozumiewania się (nadawca → wyrażenie→

odbiorca)

Poziomy Języka:

I.

Język 1 stopnia – to taka która nie odnosi się do innych
wypowiedzi, opisuje rzeczywistość (np. Łomianki leżą koło
Warszawy).

II.

Język 2 stopnia – to taki który orzeka o wypowiedzi w stopniu 1
(np

. „las” to rzeczownik; Kasia powiedziała „pupa”)

III. Itd.

IV.

Język Prawny – język w który sformułowane są Teksty prawa(język 1 stopnia).

Język prawniczy – wszelkie komentarze i interpretacje do języka prawnego(język 2 stopnia)
Glos

– komentarze do wyroków sądowych (przykład języka 3 stopnia)

Język

Naturalny(np. etniczny)

Sztuczny(nutowy zapis melodii, znaki drogowe itp.

)

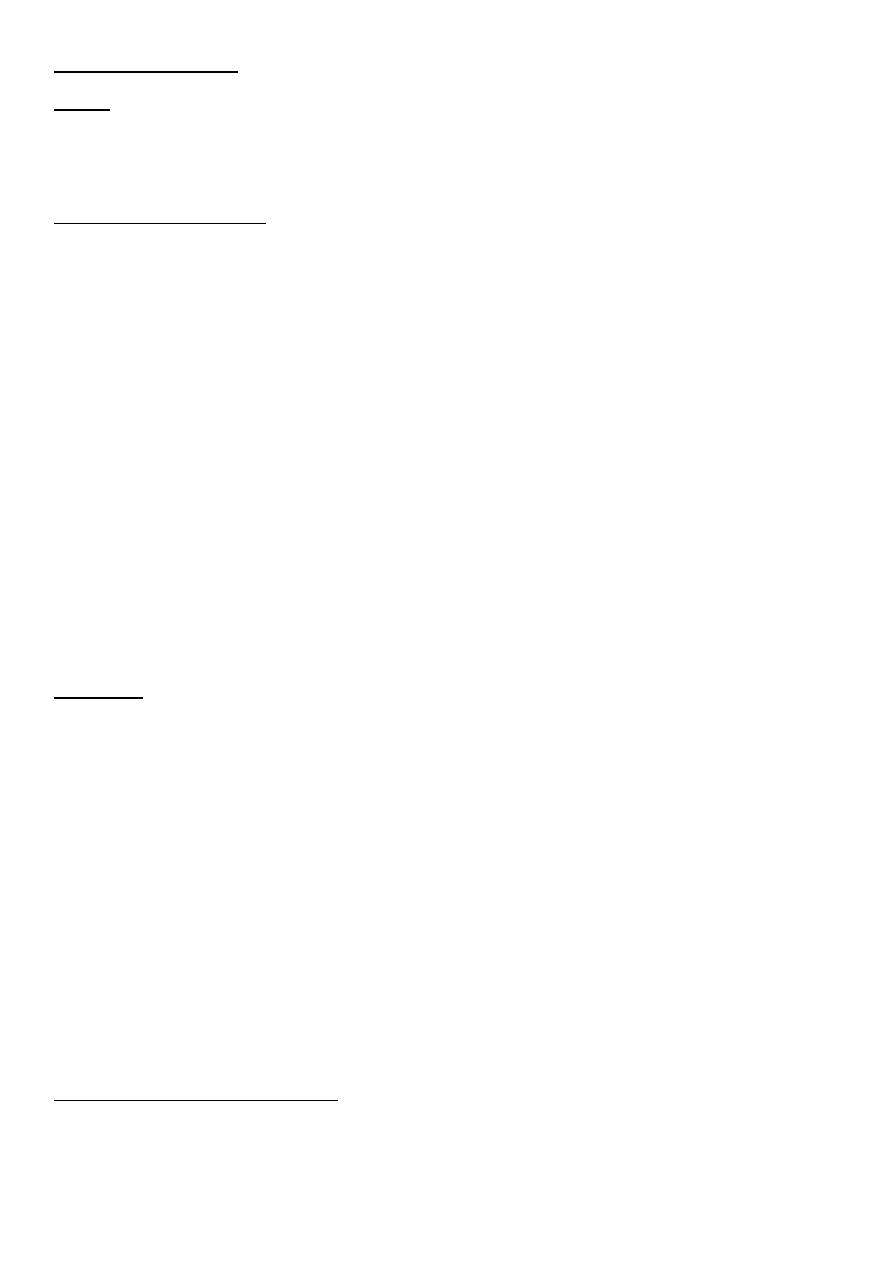
4

Kategorie syntaktyczne

Nazwa

– to podmiot „A” lub orzecznik „B” w zdaniu „A jest B” (np. Jan Kowalski, kot, 2 stycznia

2004 roku, nieruchomość, student itp.)

-

Desygnat

– przedmiot określany przez nazwę.

-

Zakres nazwy (zbiór desygnatów) – zbiór oznaczanych przez
nazwę przedmiotów

Zdanie w sensie logicznym

– wyrażenie prawdziwe bądź fałszywe (pełni funkcje stwierdzenia)

UWAGA!

– Zdaniem w sensie logicznym nie jest zdanie pytające, rozkazujące, w czasie przyszłym.

Wartość logiczna zdania –prawdziwość bądź fałszywość „0” lub „1”.

Zdania dzielimy na:

-

Zdania analityczne

– zdanie do określenia prawdziwości bądź

fałszywości którego używamy tylko jego treści (np.tydzień składa się
z siedmiu dni)

-

Zdanie syntetyczne

– wszystkie te które nie są analityczne.

Prawdziwość bądź fałszywość określamy w wyniku doświadczenia
empirycznego(np. tego

że padał deszcz możemy dowiedzieć się na

podstawie mokrej ulicy)

-

Zdania egzystencjalne

– szczególny przypadek zdań, zdania te

określają pełność bądź pustość zbioru (np. w Zakopanem jest
dworzec kolejowy)

-

Zdania subsumcyjne

– to takie które określają zależności zbiorów

(np. każdy sędzia jest prawnikiem)

-

Wypowiedzi skrótowe – są to wypowiedzi, których możemy
określić prawdziwość pewnych ściśle określonych sytuacjach,
sytuacjach nie są zdaniami w sensie normalnym.

Funktory

– to wyraz bądź wyrażenie, które nie jest nazwą ani zdaniem. Każdy z funktorów służy do

tworzenia wyrażenia złożonego.

Funktory dzielimy na:

-

Nazwotwórcze – tworzące nazwę.

-

Zdaniotwórcze – tworzące zdanie.

-

Funktorotwórcze – tworzące funktor.

Funktory zdaniotwórcze dzielimy na:

-

Ekstensjonalne

– kiedy możemy określić prawdziwość zdania na

podstawie wartości argumentów jego funktora zdaniotwórczego. Do
takich funktorów należą i; lub; albo; jeżeli… to…(i w zdaniu
jednoargumentowym) nie jest tak, że.

-

Intensjonalne

– kiedy nie możemy określić prawdziwość zdania na

podstawie wartości argumentów jego funktora zdaniotwórczego. Do
takich funktorów należą np.: jest możliwe, że; jest zakazane, aby itp.

Funktory dzielimy też ze względu na ilość ilość i jakość argumentów
N

– nazwa

Z

– zdanie

– funktor

(ble ble)

– podkreślony funktor nazywa się …

Oznaczenie tego, co tworzy funktor

Argument funktora

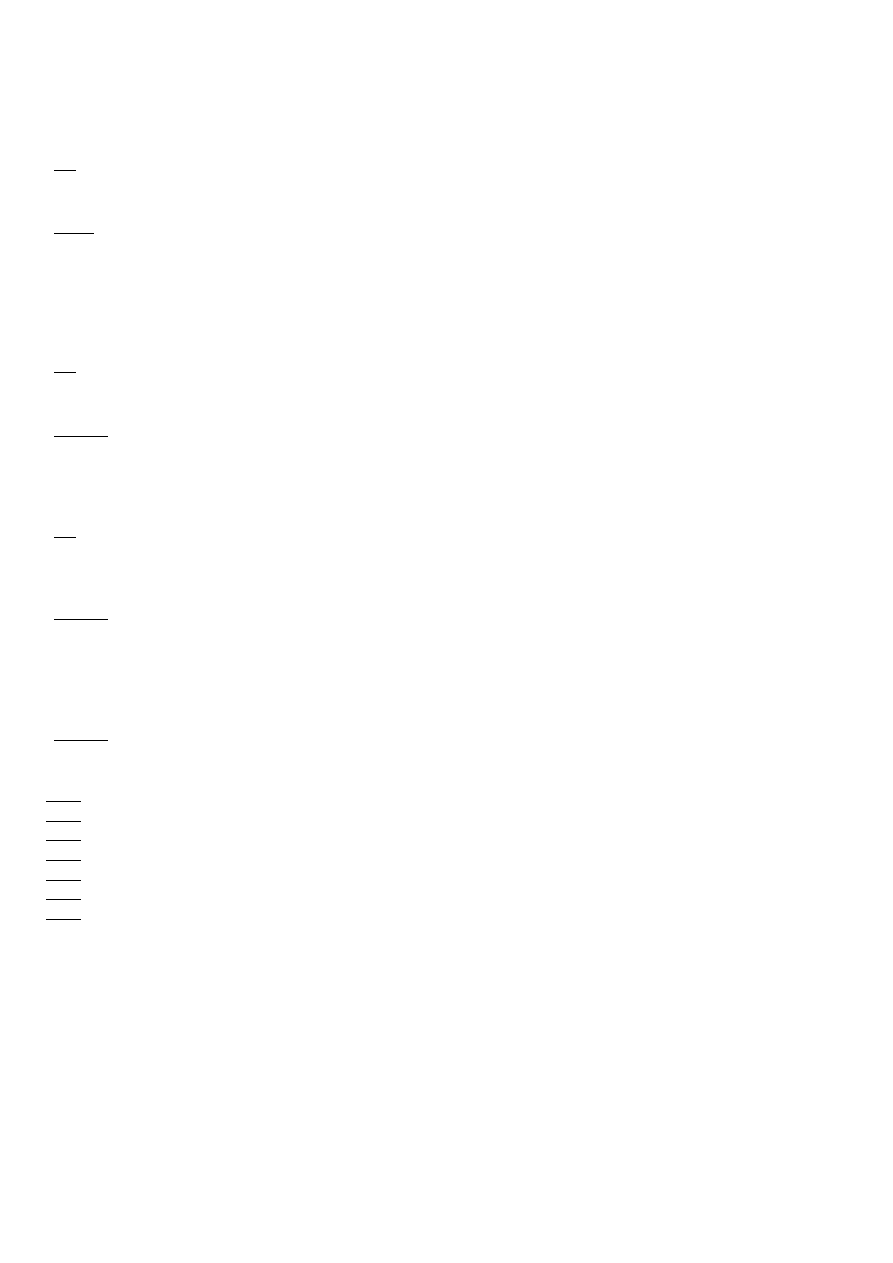
5

Przykłady
A)

Nazwotwórczy(kolor zielony = funktor)

Mądry student (funktor nazwotwórczy od jednego argumentu nazwowego)

N
N

Dziura w jezdni (funk

tor nazwotwórczy od dwóch argumentów nazwowych)

N

NN

UWAGA!

– Argumentów nazwowych może być nieskończenie wiele

UWAGA!

– Imiona i nazwiska, daty itp. nie są dwiema oddzielnymi nazwami

B) Zdaniotwórczy nazwowy

Piotr idzie

(funktor zdaniotwórczy od jednego argumentu nazwowego)

Z
N

Jan bije

Pawła (funktor zdaniotwórczy od dwóch argumentów nazwowych)

Z

NN

C) Zdaniotwórczy zdaniotwórczy
Nie jest tak, że Jan jest studentem. (Funktor zdaniotwórczy od jednego argumentu zdaniowego)

Z
Z

Chociaż Jan jest studentem, to Jan lubi chlać wódkę. (Funktor zdaniotwórczy od dwóch argumentów
zdaniowych)

Z

ZZ

D) funktory funktorotwórcze

Szybko

biegnie (funktor funktorotwórczy od jednego argumentu funktorowego)

Z

N

Bardzo szybko biegnie. (???)
Z
N
Z
N
Z
N
Z
N
„I”, „ORAZ”, „ A TAKŻE”, PRZECINEK

-

Użycie koniunkcyjne – kiedy wymieniamy czym jest dana rzecz „A
jest B i C”. W takim przypadku funktor tworzy Nawę.[Jan to student i
sportowiec]

-

Użycie Enumeracyjne – kiedy zbiór n rzeczy jest częścią innego (A
i B jest C => A jest C i B jest C)

[Jan i Romek są studentami => Jan

jest studentem i Romek jest studentem]. W takim przypadku funktor
tworzy zdanie.

-

Użycie syntetyzujące – kiedy zbiór n rzeczy należy do innego
(A+B< bądź =C)[kobiety i mężczyźni mające polskie obywatelstwo
są „polakami”].

6

Rozdział III: Nazwa, podziały nazw i stosunki zakresowe
Podziały nazw

PROSTE I ZŁOŻONE:

-

Proste

– jednowyrazowe

-

Złożone – wielowyrazowe

INDYWIDUALNE I GENERALNE:

-

Indywidualne

– przysługuje nazwie na zasadzie przyjętej konwencji

znaczeniowej, niezależnie od właściwości jakie posiada desygnat.

-

Generalna

– przypisana jest przedmiotowi ze względu na

wyodrębnioną cechę. (np. największe miasto w polsce)

NAZWY OGÓLNE, JEDNOSTKOWE JEDNOSTKOWE I PUSTE

-

Ogólna – więcej niż jeden desygnat

-

Jednostkowa

– ma jeden desygnat

-

Pusta

– nie ma desygnatów(np. obecny król Francji)

KONKRETNE I ABSTRAKCYJNE

-

Konkretna

– odnosi się do osób, rzeczy, lub ich wyobrażenia.

-

Abstrakcyjna

– wskazuje na cechy wspólne

przedmiotów(zieloność), stan rzeczy(spokój), oraz stosunek między
przedmiotami (bliskość).

ZBIOROWE I NIEZBIOROWE

-

Zbiorowe

– nazwa, która jest zbiorem złożonym z różnego rodzaju

elementów elementów wszystkie desygnaty tej nazwy tworzą zbiór w
sensie kolektywnym(tzn. element elementu zbioru jest elementem
zbioru) np. kodeks cywilny sąd okręgowy.

-

Niezbiorowe

– ma desygnaty którymi są pojedyncze przedmioty np.

student.

O ZNACZENIU STAŁYM I ZMIENNYM

-

O znaczeniu stałym – ich znaczenie nie zależy od miejsca
czasu(kot, liczby podzielne przez 2, itp.)

-

O znaczeniu zmiennym

– zależą od tego kto i kiedy posłużył się t

nazwą (ja, mój ojciec, itp.)

OSTRE I NIEOSTRE

-

Ostre

– to taka, której możemy jednoznacznie określić, że dany

przedmiot należy do jej zakresu.

-

Nieostre -

to taka, której nie możemy jednoznacznie określić, że

dany przedmiot należy do jej zakresu.

Supozycje
Supozycje

– role znaczeniowe

-

Prosta

– odnosi się do poszczególnego(konkretnego) desygnatu

nazwy

[pies zjadł kurczaka]

-

Formalna

– odnosi się do gatunku a nie poszczególnego

reprezentanta gatunku[

psy są ssakami]

-

Materialna

– odnosimy się do będącego nazwą lub wyrażeniem

wyrazu (lub grupy wyrazów)[Wyraz pies składa się z czterech liter]

Treść nazwy
Treść nazwy(konotacja)= znaczenie nazwy, na treść nazwy składa się zespół cech, które posiada każdy
jej desygnat.
Treść pełna nazwy jest rozdanie, w którym wymieniliśmy wszystkie cechy na podstawie, których możemy
zakwalifikować dany przedmiot do desygnatu danej nazwy
Cechy konstytutywne

cechy, które w sposób wystarczający określają desygnat nazwy.

Cechy konsekutywne

cechy, uzupełniające

7

Dwie nazwy są RÓWNOZNACZNE wtedy gdy mają taką samą treść.
Nazwy niewyraźne nazwy których nie możemy dokładnie określić treści.
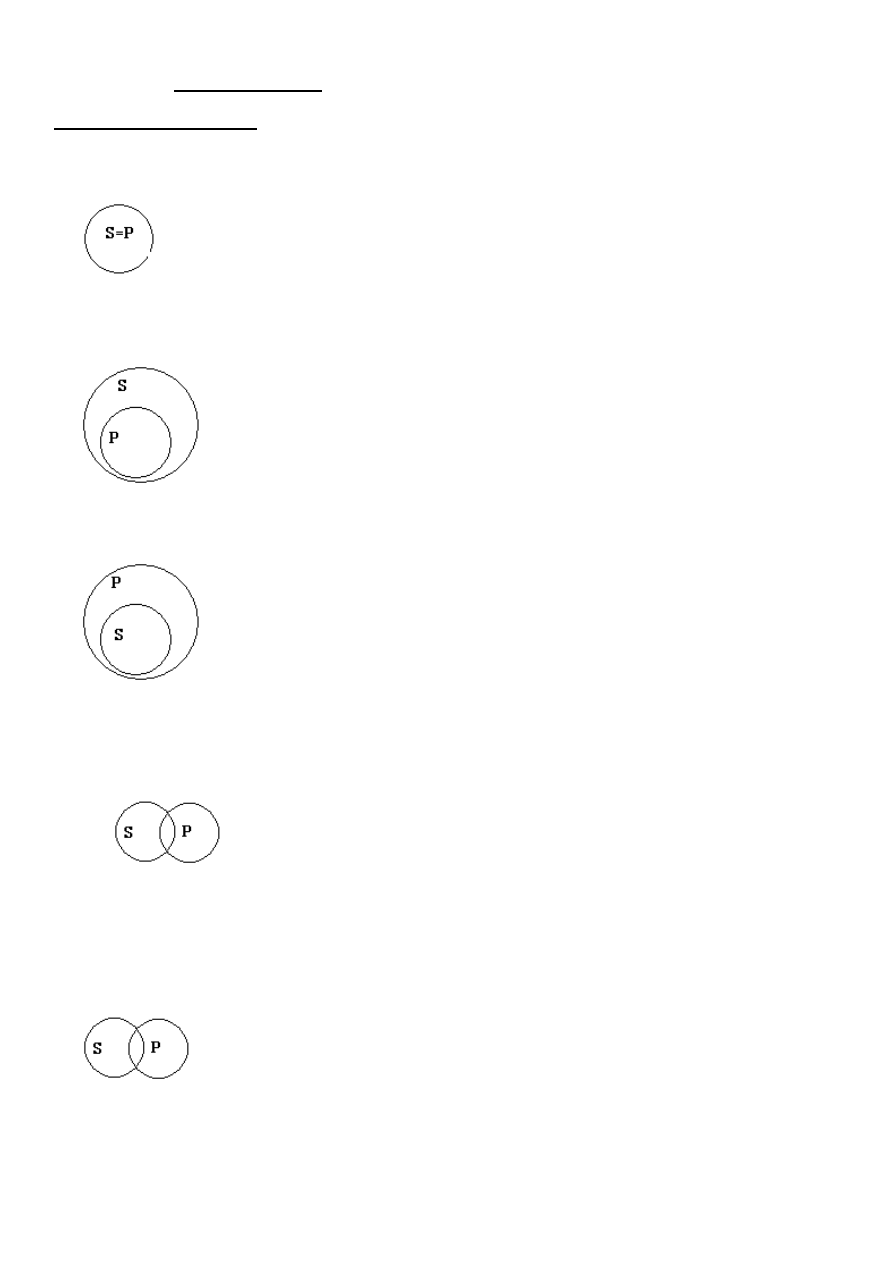
Stosunki zakresowe nazw

1.

stosunek zamienności

desygnaty „S” są zarazem desygnatami „P” i odwrotnie

S

– flaga

P

– chorągiew

2.

Stosunek nadrzędności

Każde P jest S, lecz nie każde S jest P; istnieją bowiem S, które nie są P.

S

– lekarz

P

– chirurg

3. stosunek podrz

ędności

Każde S jest P, lecz nie każde P jest S; istnieją bowiem P, które nie są S.

S

– pies

P - ssak

4.

Stosunek krzyżowania się

A)

Niezależności

B)

Niektóre S są P i niektóre P są S; istnieją bowiem S, które nie są P i istnieją P

które nie są S.
S

– prawnik

P - polityk

C)

Podprzeciwieństwa (klasa uniwersalna została wyczerpana[obejmuje wszystkie obiekty])

Niektóre S są P i niektóre P są S i poza P i S nie ma żadnych innych przedmiotów.

S

– Prawnik

P

– nie notariusz

5. Stosunek wykluczania się

8

A) Przeciwieństwa (klasa uniwersalna niewyczerpalna)

nie istnieją S, które byłyby P i nie istnieją P, które byłyby S. Oprócz S i P istnieją

inne Przedmioty.
S

– prokurator

P

– sędzia

B) sprzeczności (klasa uniwersalna wyczerpana)

n

ie istnieją S, które byłyby P i nie istnieją P, które byłyby S. Oprócz S i P nie

istnieją inne Przedmioty.
S

– sędzia

P

– nie sędzia

Rozdział V: Elementy teorii relacji

Elementy relacji
Relacje zachodzić mogą między różną ilością obiektów.
Obiekty, między którymi zachodzi określona relacja, nazywają się jej członkami.
R

(0-

∞)

– relacje

x, y, z

– członkowie relacji

Gdy istnieje

y, do którego x pozostaje w określonej relacji to x jest: Poprzednikiem relacji

Gdy istnieje y, do którego x pozostaje w określonej relacji to y jest: Następnikiem relacji
Zbiór elementów uniwersum, które są następnikami poprzednikami nazywamy: Dziedziną relacji

Zbiór elementów uniwersum, które są następnikami następnikami nazywamy: Przeciw dziedziną relacji

Dziedziną relacji jako zbiór wszystkich obiektów pozostających pozostających w relacji
R do innych obiektów oznaczamy jako D(R) i określamy:

/\

x[x є D(x)≡\/y(xRy)].

Przeciwdziedziną relacji jako zbiór wszystkich obiektów do których pewne obiekt pozostają w relacji R
oznaczamy jako i

określamy:

Stosunki między dziedziną a przeciwdziedzinąrelacji
Przeciwieństwa np. x jest mężem y
Zamienności np. x jest małżonkiem y
Krzyżowania się : x jest pozwany przez y
Nadrzędnym np. x jest postrzegany przez y
Podrzędnym np. x jest matką y
Przyporządkowania w relacjach
Gdy zachodzi między x i y relacja R to mówimy, że R przyporządkowuje x – owi y.
Relacja jednoznaczna(1

– n) – charakteryzuje się tym, że dowolny element przeciwdziedziny

przyporządkowany jest przez relacje tylko jednemu elementowi dziedziny np. x jest ojcem y

Rє n-1≡ /\x, y, z(xRy n xRz→y =z)

Relacja wzajemnie jednoznaczna(1-1) = odwrotnie jednoznaczna(1-n)

charakteryzuje się tym, że

dowolnemu elementowi dziedziny przyporządkowany jest tylko jeden element przeciwdziedziny i
wzajemnie np. x jest mężem y

Rє 1-1 ≡ R n-1 /\(małe)Rє 1-n

Wzajemnie wieloznaczna(n-n)

charakteryzuje się tym, że istnieje w jej dziedzinie przynajmniej jeden

element pozostający w tej relacji do więcej niż jednego elementu Przeciwdziedziny Przeciwdziedziną

D (R)

9

istnieje przynajmniej jeden element Przeciwdziedziną przeciwdziedzinie element, do którego pozostają w
tej relacj

i przynajmniej dwa różne elementy dziedziny.np. x został oszukany przez y.

Cechy relacji
Symetryczność
Badając symetryczność relacji, szukamy odpowiedzi na pytanie, czy ta relacja zachodzi pomiędzy x a y,
jeżeli zachodzi ona między y i x. Możliwe są tu trzy sytuacje:

-

Jeżeli zachodzi między y i x to zawsze zachodzi między x i y(relacja
symetryczna

)np. bycie rówieśnikiem. RєSym≡/\x, y(xRy→yRx)

-

Jeżeli zachodzi między y i x to nigdy nie zachodzi między x i
y(relacja asymetryczna

)np. bycie wyższym. RєAsym≡/\x,

y(xRy→~yRx)

-

Jeżeli zachodzi między y i x to czasami zachodzi między x i
y(relacja nonsymetryczna

)np. bycie lubianym. RєNonsym≡\/x,

y(Ury n yRx) n \/x,y(xRy n~yRx)

W sytuacji kiedy między x i y zachodzi R to zawsze między y i x zachodzi R

1

taką sytuacje nazywamy

konwersem relacji

np. bycie wyższym vs. Bycie niższym

R

2

=

R

1

≡/\x,y(xR

1

y≡yR

2

x)

Zwrotność

Badając zwrotność relacji, szukamy odpowiedzi na pytanie, czy x pozostaje w stosunku R do samego
siebie. Możliwe są tu trzy sytuacje:

-

X pozostaje w relacji R do samego siebie (xRx)(relacja zwrotna)np.
bycie rówieśnikiem RєZwr≡/\x(xRx)

-

X nigdy nie pozostaje w relacji R do samego siebie (relacja
zwrotna

) np. bycie poddanym RєAzwr≡/\x(~xRx)

-

X czasami pozostaje w relacji R do samego siebie (relacja
nonzwrotna)n

p. x broni y przed napadem na sklep RєZwr≡/\x(xRx)

Przechodniość
Badając przechodniość relacji R, szukamy odpowiedzi na pytanie czy relacja R zachodzi między x a z jeśli
zachodzi między x a y i y a z. Możliwe są trzy sytuacje:

-

Zawsze zachodzi relacja między x a z jeśli zachodzi między x a y i y
a z(Tranzytywna

)np. bycie starszym R єTranz≡/\x,y,z(xRy n yRz

→xRy).

-

Nigdy nie zachodzi relacja między x a z jeśli zachodzi między x a y i
y a z(Atranzytywna

)np. bycie ojcem R єAtranz≡/\x,y,z(xRy n yRz

→~xRy).

-

Czasami

zachodzi relacja między x a z jeśli zachodzi między x a y i

y a z(Nontranzytywna

)np. bycie starszym R єNontranz≡/\x,y,z(xRy

n yRz →xRy) n /\x,y,z(xRy n yRz →~xRy).

Spójność
Badanie zagadnienia spójności relacji R polega na ustaleniu polega na ustaleniu czy dwa dowolne
niejednakowe elementy z określonego zbioru pozostają w relacji R

-

Zawsze zachodzi relacja R między dwoma różnymi elementami
określonego zbioru np. bycie większą liczbą.
RєSpój(Z)≡/\x,y(xєZ n yєZ n x≠y →xRy v yRx)

-

Nigdy nie zachodzi relacja R między dwoma różnymi elementami
określonego zbioru np. bycie równą liczbą.
RєAspój(Z)≡/\x,y(xєZ n yєZ n x≠y →~[xRy v yRx])

-

Czasami zachodzi relacja R między dwoma różnymi elementami
określonego zbioru np. bycie wyższym. RєNonspój(Z)≡\/x,y(xєZ n
yєZ n x≠y →xRy v yRx) n\/x,y(xєZ n yєZ n x≠y →~[xRy v yRx])

10

Relacje szczególnego typu: porządkująca, równościowa
Porządkująca
Relacja mocno porządkująca
Niektóre z rozpatrywanych stosunków charakteryzują się tym, że za ich pomocą da się wyznaczyć w
ramach pewnego zbioru określony porządek(Relacje porządkowe)ustawiają one elementy pola relacji w
szereg, w którym każdemu elementowi wyznaczone zostaje właściwe miejsce. Musi być:

-

Spójna – musi ustalić porządek poprzedzania i następowania w
ramach każdej możliwej do stworzenia pary.

-

Asymetryczna

– musi określić, który jest porządkujący a, który

następujący

-

Przechodnia

–

Np. bycie wyższym w klasie Jan od Bolka, Bolek od Marysi a Marysia od Żelaznego golem.
Relacja słabo porządkująca

-

Asymetryczna

-

Przechodnia

Bycie wyższym w zbiorze osób gdzie przynajmniej dwie osoby są tego samego wzrostu.
Równościowa

-

Zwrotna

-

Przechodnia

-

Symetryczna

Np. równość wobec prawa
Szczególnym przypadkiem jest identyczność

Relacje jako zbiory
Relacja = zbiór par uporządkowanych
A więc między relacjami mogą zachodzić takie same związki jak między zbiorami patrz stosunki
zakresowe nazw [naciśnij prawym klawiszem myszki napis a później „otwórz hiperłącze”!!]


Stosunek zakresów Symetryczność

Przechodniość

Zwrotność

Zamienność

Symetryczny

Przechodni

Zwrotny

Nadrzędność

Asymetryczny

Przechodni

Azwrotny

Podrzędność

Asymetryczny

Przechodni

Azwrotny

Niezależność

Symetryczny

Nonprzechodni

Azwrotny

Podprzeciwieństwo Symetryczny

Nonprzechodni

Azwrotny

Przeciwieństwo

Symetryczny

Nonprzechodni

Azwrotny

Sp

rzeczność

Symetryczny

Aprzechodni

Azwrotny

Ponieważ relacje definiowane są jako zbiory uporządkowanych par liczb:
Suma <=> zachodzi jedna z relacji[R=R

1

uR

2

≡/\x, y (xRy≡xR

1

y v xR

2

y)]

Iloczyn relacji

<=>równocześnie zachodzą obie relacje[R=R

1

∩R

2

≡/\x, y(xRy≡xR

1

yn xR

2

y)]

Iloczyn względny relacji<=> inny przedmiot, który równocześnie spełnia obie
relacje[R=R

1

×R

2

≡/\x,y(xRy≡\/z(xR

1

z n zR

2

y))]

Potęga <=> R zachodzi dwukrotnie pomiędzy trzema elementami[R=(R

1

)

2

≡/\x, y(xRy≡\/z(xR

1

z n zR

1

y))]

Podział logiczny
Klasę abstrakcji „[x]

R

” relacji R wyznaczaną przez element x określamy jako zbiór wszystkich wszystkich i

tylko tych przedmiotów y, które do x pozostają w relacji R.

Yє[x]

R

≡yRx

Zasada abstrakcji

zbiór klasy relacji równościowej R jest podziałem relacji pola R.

C

ałość dzielona zakres nazwy ulegającej podziałowi

Człony podziału wydzielone w wyniku podziału zakresy

Warunki podziału:

-

Zupełność podziału – każdy desygnat nazwy dzielonej musi
należeć do zakresu któregoś z wyodrębnionych członów.

11

-

Rozłączność – każdy z desygnatów musi należeć tylko do jednej
wyodrębnionej grupy członków.

-

Treściowy – podział musi spełniać cel ze wzgl.,Na który został
przeprowadzony.

Podziały dzielą się na:
Naturalne i sztuczne:

-

Naturalne

– w którego członach znajdują się człony bardziej do

siebie podobne niż w innych członach

-

Sztuczne

– w którego członach znajdują się człony mniej do siebie

podobne niż w innych członach

Dwuczłonowe, Według zasady specyfikacji

-

Dwuczłonowe – podział przedmiotów ze wzgl. Na posiadanie jakieś
cechy( na te które ją mają i nie mają)

-

Według zasady specyfikacji(różnych odmian tej samej
cechy)Cecha według, której dokonujemy podziału determinada a jej
odmiany determinanty

Klasyfikacja
Często po przeprowadzeniu podziału jakieś nazwy dzieli się następnie wszystkie lub niektóre człony na
kolejne (2, 3, 4, … i kolejne stopnie.). Poprawny podział jest uwarunkowany wieloma zasadami:

-

Podział musi być istotny.

-

Kolejne poziomy klasyfikacji powinny być powiązane stosunkiem
bezpośredniego następstwa.

-

Inne techniczne

Typologia
Od podziałów logicznych należy odróżnić wyróżnienie typów przedmiotów.
Podział typologiczny:
Jest to podział ze wzgl. na odbieganie od typu wzorcowego, nie jest to podział logiczny bo nie spełnia
zasady rozłączności i czasami zupełności podziału.
Partycja
W przeciwieństwie do podziału logicznego(dystrybutywnego) jest podziałem zbioru kolektywnego, jest więc
wyróżnikiem pewnych części przedmiotu.

Rozdział VI: Rachunek zdań
Funkcja zdaniowa
Funkcje zdaniowe

– to wyrażenia opisowe reprezentujące strukturę (np. Każde P jest Q)wypowiedzi same

niemające wartości logicznej.
Konkretyzacją funkcji – Działanie podstawiania pod P i Q wyrazu bądź wyrażenia dzięki, któremu
możemy określić wartość logiczną.
Kwantyfikowanie

– jest to operacja polegająca na objęciu kwantyfikatorem każdej ze zmiennych

występujących w schemacie, co powoduje ich przemianę w zdania.

Funktory prawdziwościowe i nieprawdziwościowe

FUNKTORY:

-

Nieprawdziwościowe – charakteryzują się tym, że łącząc ze sobą
zdania o określonej wartości logicznej nie wyznaczają w
jednoznaczny sposób wartości logicznej zdania złożonego. Gdyż
jest on też uzależniony od treści zdania. Np. „Paryż jest stolicą
Francji” – zdanie prawdziwe. „koniecznym jest, że Paryż jest stolicą
Francji” – zdanie nie prawdziwe(np. możliwe, z tego wynika, że itp.).

-

Prawdziwościowe – charakteryzują się tym, że łącząc ze sobą
zdania o określonej wartości logicznej wyznaczają w jednoznaczny
sposób wartość logiczną zdania złożonego(np. lub, albo, bądź).

12

Funktory prawdziwościowe jednoargumentowe

-

Asercja

– jest funktorem potwierdzającym prawdziwość (np. Prawdą jest, że; zaiste;

naprawdę). A oznaczany jest przez: „≈” „─│”. NIE ZMIENIA WARTOŚCI LOGICZNEJ
ZDANIA.

-

Negacja

– zmienia wartość logiczną zdania (np. nie jest tak, że; nieprawdą jest, że).

A oznaczany jest przez „~”.

-

Sprzeczność jest wtedy gdy dwa zdani mówią o tej samej rzeczy, przy
czym jedno z nich mówi, że tak jest, a drugie, że tak nie jest.

-

Zdania przeciwne

– nie mówią o tym samym a fałszywość jednego nie

przesądza o prawdzie drugiego, choć prawdziwość jednego przesądza o
fałszywości drugiego

Funktory Prawdziwościowe dwuargumentowe

-

Koniunkcja

– związek współprawdziwości dwóch zdań(spójnikami są: np. i; przecinak).

Koniunkcje oznaczamy (P n Q)

. Jest prawdziwa <=> oba jaj człony (zdań łączonych przez

funktor użyty w znaczeniu koniunkcji) są prawdziwe

P

Q

P n Q

1

1

1

1

0

0

0

1

0

0

0

0

-

Alternatywa Zwykła – związek niewspółfałszywości dwóch zdań(lub). Alternatywę

zwykłą oznaczamy (P v Q).Jest fałszywa tylko wtedy kiedy oba (człony zdań łączonych
przez funktor użyty w znaczeniu alternatywy) są fałszywe.

P

Q

P v Q

1

1

1

1

0

1

0

1

1

0

0

0

-

Alternatywa rozłączna – związek niezgodności dwóch zdań pod wzgl. prawdy i

fałszu(albo; [albo…, albo]).Jest prawdziwa jeżeli łącz one przez nią zdania mają różną
wartość logiczną. Alternatywę rozłączną oznaczamy „_|_”

P

Q

P _|_ Q

1

1

0

1

0

1

0

1

1

0

0

0

-

Dysjunkcja

– związek niewspółprawdziwości dwóch zdań(bądź;

[bądź, … Bądź]). Jest prawdziwa <=> co najmniej jedno zdanie składowe jest fałszywe.
Dyskusje oznaczamy (P / Q).

P

Q

P / Q

1

1

0

1

0

1

0

1

1

0

0

1

-

Binegacja

– związek współfałszywości dwóch zdań(ani;[ani,…ani]). Jest prawdziwa

tylko wtedy gdy oba zdania składowe są fałszywe. A oznaczana jest (P↓Q)

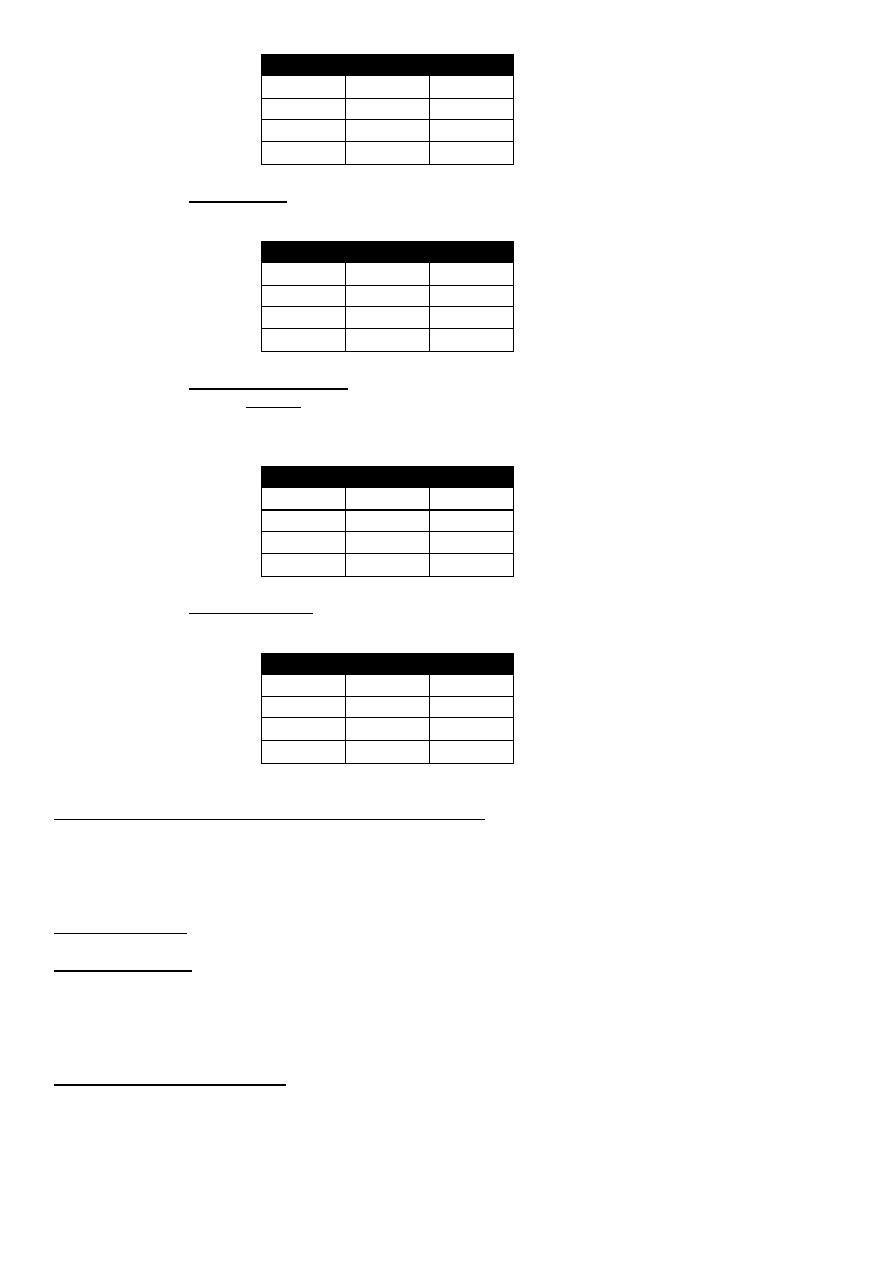
13

P

Q

P

↓ Q

1

1

0

1

0

0

0

1

0

0

0

1

-

Implikacja

– związek strukturalnoprawdziwościowy (jeżeli …,to…). Jest prawdziwa gdy

oba zdania składowe są prawdziwe, kiedy oba zdania składowe są fałszywe lub kiedy
poprzednik jest fałszywy a następnik prawdziwy. Implikacja jest oznaczana(P → Q).

P

Q

P

→ Q

1

1

1

1

0

0

0

1

1

0

0

1

-

Implikacja odwrotna

– występuje tylko w przypadkach kiedy jeżeli to zostanie użyty w

znaczeniu „zawsze gdy jakiś warunek zostanie spełniony to coś się stanie”(tylko jeżeli to).
Jest prawdziwa, gdy oba zdani

a składowe są prawdziwe, kiedy oba zdania składowe są

fałszywe lub, kiedy poprzednik jest prawdziwy a następnik fałszywy. Implikacja jest
oznaczana (P ← Q).

P

Q

P

← Q

1

1

1

1

0

1

0

1

0

0

0

1

-

Równoważność – związek prawdziwościowy (wtedy i tylko wtedy gdy może zostać

użyty spójnik jeżeli to ale tylko w przypadku [Jeżeli P to Q]=[Jeżeli Q to P] ). Jest prawdziwa
gdy oba człony są fałszywe i kiedy oba są prawdziwe. A oznaczana jest (P ≡ Q)

P

Q

P

≡ Q

1

1

1

1

0

0

0

1

0

0

0

1

Funktory prawdziwościowe, trój- i więcej argumentowe
Koniunkcja

– jeśli wszystkie człony są prawdziwe

Alternatywa zwykła trójczłonowa – fałszywa tylko wtedy gdy wszystkie człony fałszywe
Dysjunkcja

– fałszywa jeśli wszystkie zdania składowe są prawdziwe

Alternatywa trójczłonowa rozłączna – wtedy gdy prawdziwy jest tylko jeden z jej członów

Funkcje logiczne

Funkcja logiczna

w rachunku zdań to funkcja zdaniowa, która zbudowana jest jedynie ze stałych

logicznych i zmiennych(zdaniowych lub nazwowych).

Stałe logicznie = omówione wyżej funktory

prawdziwościowe. Zmienne zdaniowe oznaczone symbolami p, q, r, s, …reprezentujące dowolne zdania w
sensie logicznym np. [(p→ r)n(q→ r)n(p v q)] →r {i określamy wartość logiczną poszczególnych
nawiasów ????}.

Funkcje logiczne dzielimy na:

- Funkcje tautologiczne

– to jest takie, które dla każdego podstawienia wartości

zmiennych zawsze dają zdanie prawdziwe.

- Funkcje kontrtautologiczne -

to jest takie, które dla każdego podstawienia wartości

zmiennych zawsze dają zdanie fałszywe.

14

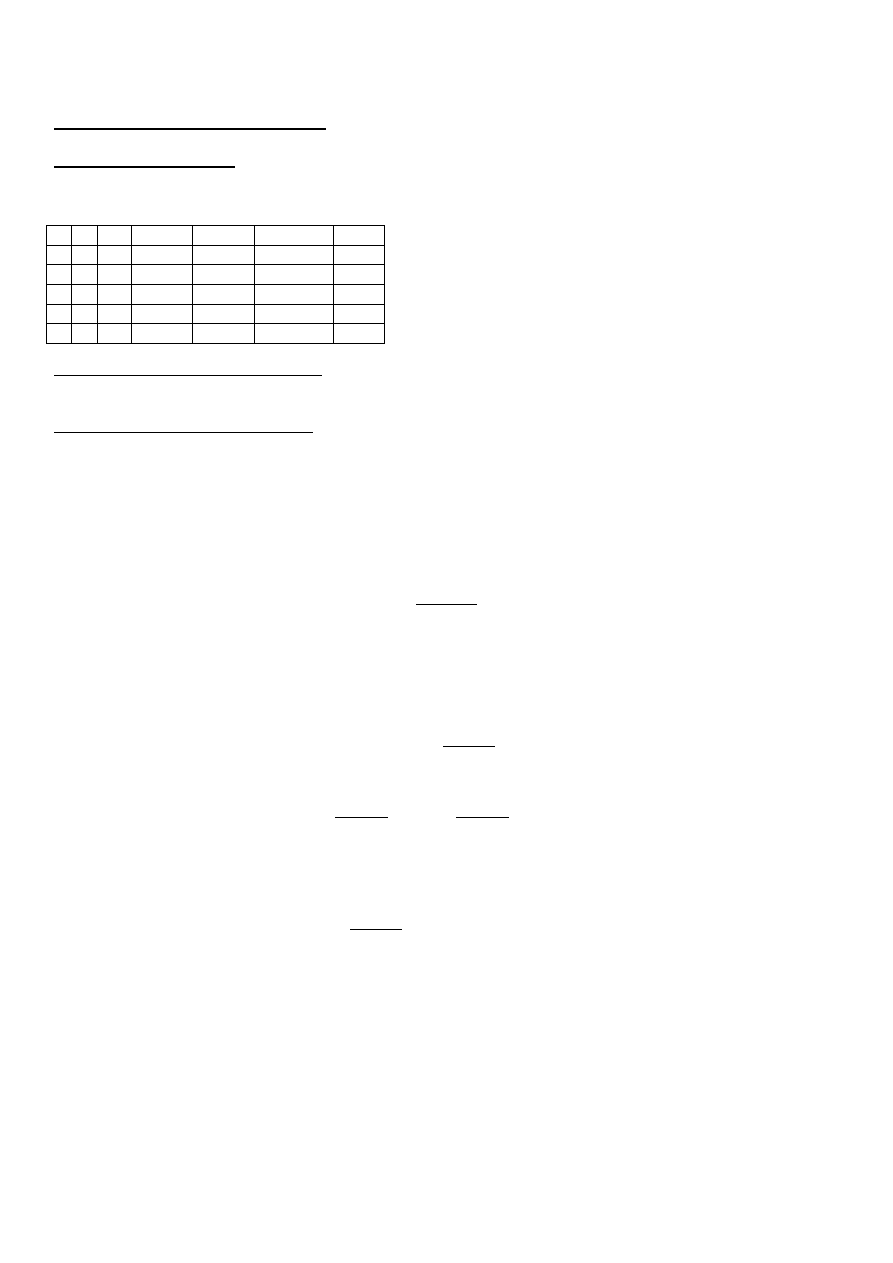
- Funkcje specjalne

– które przy niektórych zmiennych dają zdanie prawdziwe a przy

niektórych fałszywe.

Metody badania funkcji logicznych

Metoda zerojedynkowa

– polega na kolejnym podstawianiu pod zmienne zer lub jedynek(funkcja jest

tautologiczna,

jeśli wszystkie możliwe przypadki dają prawdę)

Przykład 1.
(p → q) →~(p n ~q)

Ta funkcja jest tautologią ponieważ w ostatniej kolumnie są
same jedynki.

Metoda na dowodzenie nie wprost

polega na przyjęciu założenia, że ta funkcja nie jest

tautologią(zaczynamy odwrotnie niż poprzednio tj. na początku zakładamy, że jest nieprawdziwe a później
sprawdzamy na kolejnych szczeblach w jakim przypadku jest to możliwe)
Meto

da dowodów założeniowych – Metoda ta polega na tym, że przyjmujemy określone schematy

formalne bez dowodu, uznając, że są niezawodne. Schematy te nazywamy schematami pierwotnymi, a
zdania stwierdzające ich niezawodność – regułami pierwotnymi. Opierając się na niezawodności
schematów pierwotnych, dowodzimy niezawodności innych schematów formalnych, które nazywamy
schematami wtórnymi.
Regułami pierwotnymi są:

-

Reguła odrywania(RO) – prawdziwość implikacji i jej poprzednika przesądza o
prawdziwości następnika.

p → q
P
q

-

Reguła dołączenia koniunkcji (DK) – reguła ta stwierdza, że z dwóch prawdziwych
wyrażeń zdaniowych wynika prawdziwość ich koniunkcji

p
q

p n q

-

Reguła opuszczenia koniunkcji (OK) – Z prawdziwości koniunkcji wynika prawdziwość
każdego z jej czynników.

-

Reguła dołączenia alternatywy (DA) – reguła ta stwierdza, że z prawdziwości jednego ze
członków alternatywy wynika prawdziwość alternatywy

1 2 3

4

5

6

7

p q ~q

p → q p n ~q ~(p n~q) 4→6

1 1

0

1

0

1

1

1 0

1

0

1

0

1

0 1

0

1

0

1

1

0 0

1

1

0

1

1

q n p

q

p n q

p

p

p v q

q

p v q

15

-

Reguła opuszczania alternatywy (OA) – reguła ta stwierdza, że z prawdziwości
alternatywy i negacji jednego z jej składników wynika prawdziwość drugiego

-

Reguła dołączenia równoważności (DE) – reguła ta stwierdza, że z implikacji i implikacji
jej odwrotnej wynika

równoważność

-

Reguła opuszczania równoważności (OE) - reguła ta stwierdza, że z równoważności

wynika implikacja i implikacja do niej odwrotna

Przykład 1.

[(p → q) n (q → r) ] →(p → r)

1.

p → q (założenie)

2.

q → r (założenie) [p (założenie)

3. q (RO 1, 3)

[z założenia RO punktu 1 i 3 wynika, że q jest prawdziwe]

4. r (RO 2,4)

[dzięki poprzedniemu założeniowi wiemy, że q jest prawdą, koleinie z założenia RO

punktu 2 i 4 r jest prawdziwe]

Przykład 2.

~(p n ~q)

1.

p n ~q (założenie dowodu niewprost)

2.

p (OK 1)[z założenia OK punktu 1 wynika, że p jest prawdziwe]

3. ~p (OK 1)

[z założenia OK punktu 1 wynika, że p jest prawdziwe, po zaprzeczeniu fałszywe]

4.

sprzeczność 2, 3 [funkcja w nawiasie jest nieprawdziwa ,

Przed nawiasem jest zaprzeczenie

a więc ta funkcja jest tautologią

Reguły przekształcania rachunku



Podstawianie

– polega na tym, że w miejsce pewnych zmiennych w danym wzorze

umieszczamy wybrane dowolnie funkcje lub zmienne.



Zastępowanie – polega na tym, że zamiast określonej funkcji logicznej będącej

częścią przekształconego wyrażenia, wstawiamy inną funkcję, która jest równoważna
logicznie funkcji zastępowanej(czyli takie, które przyjmują jednakową wartość logiczną przy
tym samym podstawieniu np.



(p → q) i (~p v q)



(p n q) i ~(~p v ~q),



(p v q) i (~p → q)



(p/q) i ~(p n q)



(p v q) i (~p/~q)



Reguła odrywania – polega na tym, że w określonej funkcji należącej już do

systemu aksjologicznego a mającej postać implikacji lub równoważności opuszczamy
poprzednik o ile

przyjęliśmy go poprzednio do systemu. (?????)

Prawa logiczne



Zasada tożsamości(principimum identitalis) (p → p)



Zasada niesprzeczności(principium non contradicitonis) ~(p n ~p)



Zasada wyłączonego środka(principium terii exclusi) (p v ~p)



Zasada podwójnego przeczenia ~(~p)≡p



Prawo redukcji do absurdu

(p→ ~p) →~p

p v q

~p

q

p v q

~q

p

p → q
q

→ p

p ≡ q

p ≡ q
q → p

p ≡ q
p → q

16



Sylogizm konstrukcyjny(modus ponendo pones)

[(p → q) n q] →q



Sylogizm destrukcyjny(modus tollendotollens

) [(p→q) n ~q] →~p



Sylogizm alternatywny(modus tollendo ponens)

1.

[(p v q) n ~p] → q

2.

[(p v q ) n ~q] →p



Sylogizm dysjunkcyjny (modus ponendo tollens)
1.

[(p/q) n p] →~q

2.

[(p/q) n q] → ~p



Sylogizm alternatywno rozłączny
1.

[(p _|_ q) n p] → ~q

2.

[( p_|_ q) n q] → ~p

3.

[( p_|_ q) n ~p] → q

4.

[(q _|_ p) n ~q] → p



Sylogizm równościowy
1.

[(p ≡ q) n q] → p

2.

[(p ≡ q) n p] → q

3.

[(p ≡ q) n ~q] →~p

4. [

(p ≡ q) n ~p] →~q



Prawo transpozycji prostej

(p → q) → (~q → ~p)



Pierwsze prawo de Morgana

~(p n q) → (~p v ~q)



Drugie prawo de Morgana ~

(p v q) → (~p n ~q)



Charakterystyka prawdy

q →(p → q)



Charakterystyka fałszu ~p → (p → q)



Prawo Dunsa Szkota

(p n ~q) → q



Prawo negowania implikacji

~(p → q) → (q → p)



Prawo sylogizmu hipotetycznego koniunkcyjnego

[(p → q) n (q → r)] → (p → r)



Prawo sylogizmu hipotetycznego bezkoniunkcyjnego

(p → q) → [(q → r) → (p → r)]



Prawo transpozycji złożonej
1.

[(p n q) → r] → [(p n ~r) → ~q]

2.

[(p n q) → r] → [(~r n q) → ~p]



Prawo impostacji i eksportacji(uwaga koniecznie zajrzeć do książki) składa się z

[(p n q) → r] → [p → (q → r)] oraz [p → (q → r)] → [(p n q) → r]



Prawo dylematu destrukcyjnego prostego

[(r → p) n (r → q) n (~p~ v q)] → ~r



Prawo dylematu prostego

[(p → r) n (q → r) n (p v q)] → r



Prawo mnożenia implikacji [(p → q) n (r → s)] → [(p n r) → (q n s)]



Prawo dodawania implikacji

[(p → q) n (r → s)] → [(p v r) →(q v s)]



Prawo dylematu konstrukcyjnego złożonego [(p → q) n (r → s) n (p v r)] → (q v s)



Prawo dylematu destrukcyjnego złożonego [(p → q) n (r → s) n (~q v ~s)] → (~p v ~r)

Rozdział VII: Elementy rachunku Predykatów
Podstawowe pojęcia
Nazwa jednostkowa

– to taka, która ma tylko jeden desygnat

Nazwy indywidualne - prz

ysługuje nazwie na zasadzie przyjętej konwencji znaczeniowej, niezależnie od

właściwości, jakie posiada desygnat.
Nazwy generalne

– desygnat takiej nazwy jest wyróżniony ze wzgl. na cechy

Deskrypcje

– niektóre z nazw generalnych mające tylko jeden desygnat, będące jednocześnie nazwami

indywidualnymi.(Najwyższy budynek w Warszawie, granica między RP i Litwą). Jest zbudowana z
Argumentu/Argumentów tzn. jest złożona z jednej lub więcej jednostkowej nazw indywidualnych oraz
wyróżnienia. Wyróżnienie jest funktorem nazwotwórczym od tylu nazw ile jest nazw indywidualnych, nazwy
generalne stają się częścią funktora=> Deskrypcyjny funktor nazwowy.
Term

– jednostkowe nazwy indywidualne i deskrypcje

Predykat

– wyrażenie, które w połączeniu z jednym lub więcej termów tworzy zdanie

- Predykat jednoargumentowy

– czyli taki, który tworzy zdanie tylko z jednym

termem(np. Piotr uczy się)

- Predykat dwuargumentowy

– czyli taki, który tworzy zdanie z dwoma termami(np. Jan

jest wyższy od Pawła)

- Predykat trzyargumentowy

– czyli taki, który tworzy zdanie z trzema termami(np. .10

podzielone przez 5 daje 2)

- Predykat n

–argumentowy - czyli taki, który tworzy zdanie z n termami

17

Kwantyfikator ogólny – reprezentowany jest wyrażeniem „dla każdego”, „dla wszystkich” a graficznie jest
zapisywa

ny Π,/\ i inne.

Kwantyfikator szczegółowy – reprezentowany jest przez wyrażenie „istnieje”, „dla pewnego”,

„dla niektórych”, niektórych graficznie jest przedstawiany np. \/, ∑

Zasięg kwantyfikatora – wyrażenie, do którego odnosi się kwantyfikator
Zmienna

związana – zmienna kwantyfikatora

Rozdział VIII: Teoria nazw
Zdanie kategoryczne
Wyróżniamy cztery zdania kategoryczne:

Zdanie ogólno-twierdzące – „każde S jest P” = (S a P)

Zdanie ogólne-przeczące – „Żadne S nie jest P” = (S e P)

Zdanie szczegółowo-twierdzące – „Niektóre S są P” = (S i P)

Zdanie szczegółowo-przeczące – „Niektóre S nie są P” = (S o P)

Zdania te dzielimy według:

„ilości” na ogólne(S a P, S e P) i szczególne(S i P, S o P)

„jakości” na twierdzące(S a P, S i P) i przeczące(S e P, S o P)

Interpr

etacja mocna zdań kategorycznych – założenie, że nazwy występujące w zdaniach nie są puste

Interpretacja słaba – dokonujemy przez zamianę wyrażeń każde i żadne na słowo wszelki

Zdanie S a P jest prawdziwe tylko dla dwóch stosunków zakresowych:



Zamienność



Podrzędność

Zdanie S e P prawdziwe tylko dla dwóch stosunków zakresowych:



Przeciwieństwo

 S

przeczność

Zdanie S i P prawdziwe tylko dla 5 stosunków zakresowych



Zamienność



Podrzędność



Nadrzędność



Niezależność



Podprzeciwieństwo

Zdanie S o P prawdziwe tylko dl

a 5 stosunków zakresowych



Przeciwieństwo



Sprzeczność



Nadrzędność



Niezależność



Podprzeciwieństwo

Zdania kategoryczne poprzedzone słowem „tylko”
Np.



Tylko S a P prawdziwy jest tylko stosunek nadrzędności i zamienności

 Tylko S e P

Ten podział pozwala wprowadzić dwie zawsze prawdziwe zależności:



Tylko S e P ≡ nie-S a P



Tylko S e P ≡ nie-P a S

2

 Tylko S i P

(nadrzędność, niezależność, Podprzeciwieństwo)

Ten podział pozwala wprowadzić prawdziwą zależność:



Tylko S i P ≡ (S i P n S o P)

 Tylko S o P

(nadrzędność, niezależność, Podprzeciwieństwo)

Ten podział pozwala wprowadzić prawdziwą zależność:



Tylko S o P ≡ (S o P n S i P)

Tylko S i P ≡ Tylko S o P
Kwadrat logiczny



Strzałki oznaczają wynikanie



Linia przerywana łączy zdania pozostające w stosunku przeciwieństwa



Linia przerywana z kropkami zdania podprzeciwne

S a P

S e P

S o P

S i P

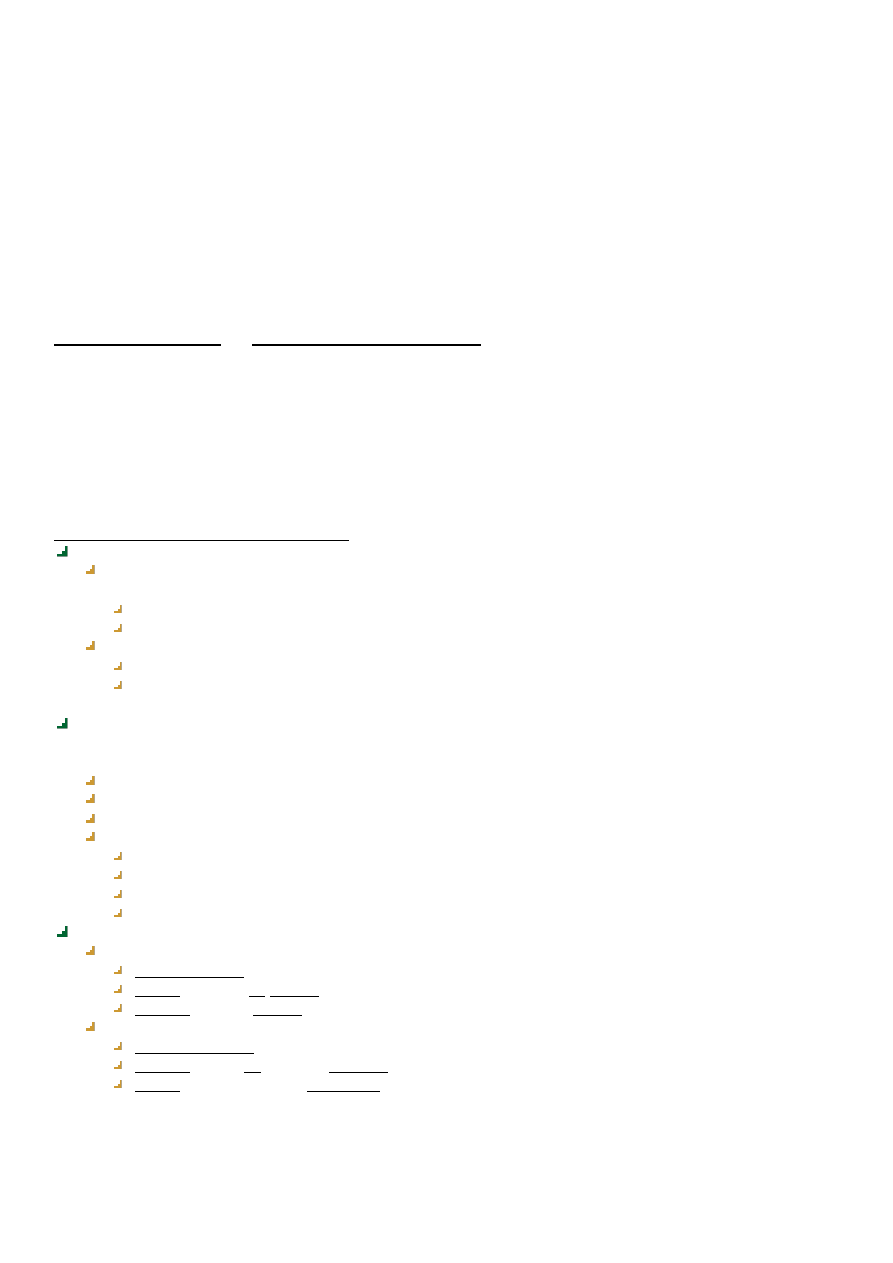
18



Ciągła sprzeczne



Para zdań S a P – S o P jest przykładem zdań sprzecznych oznacza to, że jedno ze
zdań jest negacją drugiego tzn. Jeżeli S a P jest prawdziwe to S o P fałszywe, a
kiedy S a P jest fałszywe to S o P jest prawdziwe i odwrotnie. {tak samo jest z S i P ,
S e P}.



Między zdaniami ogólnymi S a P oraz S e P zachodzi stosunek przeciwieństwa
oznacza to, że są niewspółprawdziwe (Zdania przeciwne) tzn., że zachodzą tylko
przypadki (0,0)(0,1)(1,0).



Podprz

eciwieństwo zachodzi między zdaniami S i P oraz S o P, jako zdania

Niewspółfałszywe zachodzą tylko trzy relacje: (1,1)(0,1)(1,0)



Zdanie S i P jest

Podporządkowane zdaniu S a P inaczej mówiąc ze zdania S a P

wynika zdanie S i P (0,0)(0,1)(1,1){tak samo S e P oraz S o P}

„PRAWA OPOZYCJI” lub „KWADRATU LOGICZNEGO”



S a P _|_ S o P



S e P _|_ S i P



S a P / S e P



S i P v S o P



S a P → S i P



S e P → S o P

Przekształcanie zdań kategorycznych

Konwersja zdań kategorycznych

Konwersja Prosta

– Polega na zmianie miejscami podmiotu z orzecznikiem(możliwe tylko w

zdaniach typu S e P oraz S i P)np.

S e P ≡ P e S

S i P ≡ P i S

Konwersja ograniczona

– dotyczy zdań typu S a P a jej ograniczoność polega na;

Zdanie ogólne zostaje przekształcone na zdanie szczegółowe

Funktorem

głównym tego prawa logicznego nie jest równoważność lecz implikacja



S a P → P i S

Obwersja

– sprowadzają się do zmiany jakości zdania kategorycznego kategorycznego jednoczesnym

zanegowaniem orzecznika. Co istotne, zasada ta sprawdza się w przypadku wszystkich czterech zdań
kategorycznych. Składa się z czterech elementów;

Nie ma zmiany ilości zdania

Następuje zmian jakości zdania

Podmiot pozostaje podmiotem a orzecznik orzecznikiem
Orzecznik pozostaje zanegowany

S a P ≡ S e ~P

S e P ≡ S a ~P

S i P ≡ S o ~P

S

o P ≡ S i ~P

Kontrapozycja

Kontrapozycja częściowa – polega na przeprowadzeniu Obwersja a później konwersji

S a P ≡ ~P e S

S e P

≡ S a ~P → ~P i S (kontrapozycja ograniczona)

S o P ≡ S i ~P ≡ ~P i S

Kontrapozycja zupełna – polega na kolejny przeprowadzeniu Obwersja, konwersji i Obwersja

S a P ≡ ~P a ~S

S e P ≡S a ~P → ~P i S ≡ ~P o ~S(kontrapozycja ograniczona)

S o P

≡ S i ~P ≡ ~P i S ≡ ~P o ~S

19

Sylogizm kategoryczny
Sylogizm kategoryczny

– jest to taki sylogizm, w którym zarówno przesłanki jak i wnioski są zdaniami

kategorycznymi. Składa się:

-

Terminu średniego – tego który powtarza się w przesłankach

-

Terminu większego – termin będący orzecznikiem koniunkcji sylogizmu

-

Terminu mniejszy

– termin będący podmiotem koniunkcji sylogizmu

Przesłanka większa – ta, w której występuje termin większy
Przesłanka mniejsza – ta, w której występuje przesłanka mniejsza

-

Przesłanka większa

-

Przesłanka mniejsza

M

– termin średnia

P

– Termin większy

S

– Termin mniejszy

Można też to zapisać: (M a P n S a M) → S a P

Figury sylogistyczne
Figury sylogistyczne rozróżnia się ze względu na położenie terminu średniego:
Figura 1:

Figura 2:

Figura 3:

Figura IV:

Po podstawieniu zdań ogólnych, szczegółowych, przeczących i twierdzących możemy zbudować 256
schematów, czyli trybów sylogistycznych. Tylko po 6 schematów na każdą figurę jest poprawnych, czyli
słuszne czyli takich w których których przesłanek wynika logicznie wniosek.

Zasady poprawności trybu sylogistycznego
Metoda 1:



W poprawnym trybie co najmniej jedna

przesłanka musi być twierdząca i co najmniej jedna

musi być ogólna



Jeśli dwie przesłanki są twierdzące, wniosek musi być twierdzący. Jeśli jedna przesłanka jest
przecząca wniosek musi być przeczący



Termin średni M musi być rozłożony przynajmniej w jednej przesłance(rozłożone są te czesi
zdania kategorycznego,

które są zielone)

Każdy występek jest przestępstwem
Każda bigamia jest występkiem
Każda bigamia jest przestępstwem

M a P
S a M
S a P

M P
S M
S P

P M
S M
S P

M P
M S
S P

P M
M S
S P

S

a P

S

e

P

S o

P

S i P

20



Jeśli termin jest rozłożony we wniosku musu być rozłożony w przesłance



Termin średni musi być użyty w obu przesłankach w tym samym znaczeniu(jeśli nie jest mamy
błąd czterech terminów)

Metoda 2:
Zasady:
Zdanie S a P

Zdanie S e P

Zdanie S i P

Zdanie S o P

rozwiązywanie:

-

Zaznaczamy na układzie trzech kół przesłanki

- Odczytujemy konkluzje

Błąd formalny i materialny
Błąd formalny - gdy wniosek nie wynika z przesłanek
Błąd materialny – powstaje, gdy traktujemy przesłankę jako prawdziwą a jest fałszywa

Rozdział IX: Uzasadnianie twierdzeń
Uzasadnianie bezpośrednie i pośrednie
Uzasadnianie bezpośrednie polega na wykorzystaniu w procesie uzasadniania zdań wyłącznie naszych
doznań zmysłowych.
Uzasadnianie pośrednie uzasadnianie na podstawie uznania prawdziwości pewnego zdania

Bezpośrednie

Spostrzeżenie – operacja polegająca na zarejestrowaniu postrzeżenia łączącego się z jednoczesnym
wykorzystaniem zasobów naszej wiedzy.
Obserwacja

– uporządkowany ciąg spostrzeżeń.

Eksperyment

– Obserwacja w sztucznie wytworzonych warunkach

 Pozytywny

– że zachodzi zależność pomiędzy czynnikami A i B(nigdy do końca nie potwierdza)

 Negatywny

– że nie zachodzi zależność pomiędzy czynnikami A i B

21

Pośrednie

Implikacja

– jest funktorem prawdziwościowym łączącym zmienne zdaniowe lub zdania a zdanie w ten

sposób jest fałszywe tylko wówczas kiedy pierwsze zdanie składowe jest prawdziwe a drugie fałszywe.
Wynikanie

– (Gdy ze zdania Z

1

zdanie Z

2

mówimy, że zdanie Z

1

jest racj

ą zdania Z

2

, zdanie Z

2

zaś jest

następnikiem zdania Z

1

)

Ze zdania Z

1

wynika zdanie Z

2

gdy spełnione są łącznie dwa warunki:



Implikacja zbudowana ze zdania Z

1

jako poprzednika i zdania Z

2

jako

następnika jest prawdziwa.



Pomiędzy zdaniem Z

1

i zdaniem Z

2

zachodzi pewie

n związek o

charakterze treściowym

lub strukturalnym gwarantujący to, że prawdziwość

zdania Z

1

pociąga za sobą prawdziwość zdania Z

2.

Ze zdania Z

1

wynika logicznie zdanie Z

2

wtedy i tylko wtedy, gdy implikacja Z

1

→ Z

2

jest konkretyzacją

tautologii. Innymi s

łowy, implikacja Z

1

→ Z

2

powstaje z tautologii

przez zastąpienie stałymi wszystkich

zmiennych.

Związki:



O charakterze analitycznym

– racja i następstwo są złożone jedynie ze

wzgl. na sens użytych w tym zdaniu słów (Jeżeli Piotr jest wyższy od Pawła,
to P

aweł jest niższy od Piotra)



O charakterze przyczyno-skutkowym

– wiąże się on ze związkami

empirycznymi, jakie zachodzą między zjawiskami opisywanymi w zdaniach
złączonych wynikaniem (Jeżeli temperatura spadnie poniżej zera to woda w
stawie zamarznie)



O charakterze strukturalnym

– jest on związany z rozmieszczeniem

zdarzeń lub przedmiotów w czasie lub przestrzeni. („jeżeli dziś jest 7 maja to
za tydzień będzie 14 maja” „Jeżeli polecę na N samolotem to dolecę do
bieguna N.”)



O charakterze tetycznym

– wynika z ustanowień określonych norm

prawnych[lub innych](

„Jeżeli ktoś jest ojcem, to powinien zapewnić

małoletnim dzieciom środków utrzymania”).

Wnioskowanie:



Niezawodne

–na podstawie prawdziwości pewnego zdania lub kilku zdań będących

przesłankami stwierdzamy prawdziwość innego zdania będącego wnioskiem.
Wnioskowania tego typu są oparte o niezawodne schematy inferencyjne o postaci
implikacji. (prawdziwość przesłanek potwierdza prawdziwości wniosku)



Zawodne

– polega na stwierdzeniu na podstawie uznanego za prawdziwe zdania lub zdań

innego zdania(wniosku) z określonym stopniem prawdopodobieństwa. (prawdziwość
przesłanek nie potwierdza prawdziwości wniosku)

WNIOSKOWANIA DZIELIM TEŻ NA:



Wnioskowanie dedukcyjne

– to takie które opierają się na wynikaniu logicznym, gdzie uznana za

prawdziwą jest racja(oparte o niezawodne schematy inferencyjne)[NIEZAWODNE!!]



Sensu stricte

– kiedy mamy uznaną rację i badamy jakie jest jej następstwo



Dowodzenie

– gdy poszukujemy uznanej racji dla określonego nieznanego jeszcze następstwa



Wprost

– Polega na wskazaniu przesłanek będących uznanymi racjami z, których wynika

udowodnione zdanie



Niewprost

– polega na tym, że dokonuje się zanegowania zdania dowodzonego, a następnie

dochodzi się poprzez reguł dowodzenia do zaprzeczenia jakiegoś już uprzednio udowodnionego
zdania



Wnioskowanie niededukcyjne

– to takie, które opierają się na związkach innych niż wynikanie

logiczne[ZAWODNE!!]

(związek między przesłanką a wnioskiem nie opiera się na implikacji lecz na

związkach o innym charakterze).



Tłumaczenie – dla pewnego następstwa uznanego za prawdziwe(w tym rozumieniu będącego
przesłanką) szuka się prawdziwej racji (w tym rozumieniu będącej wnioskiem)



Sprawdzenie

– jest to rozumowanie polegające na tym, że uważając jakieś zdanie za prawdziwe,

szukamy

jego następstw, aby z ich prawdziwości bądź fałszywości wnosić o wartość logiczną

zdania sprawdzanego.



Sprawdzanie pozytywne

– dla zdania znajdujemy następstwa prawdziwe i wtedy choć jedynie z

pewnym prawdopodobieństwem, wnioskujemy o jego prawdziwości

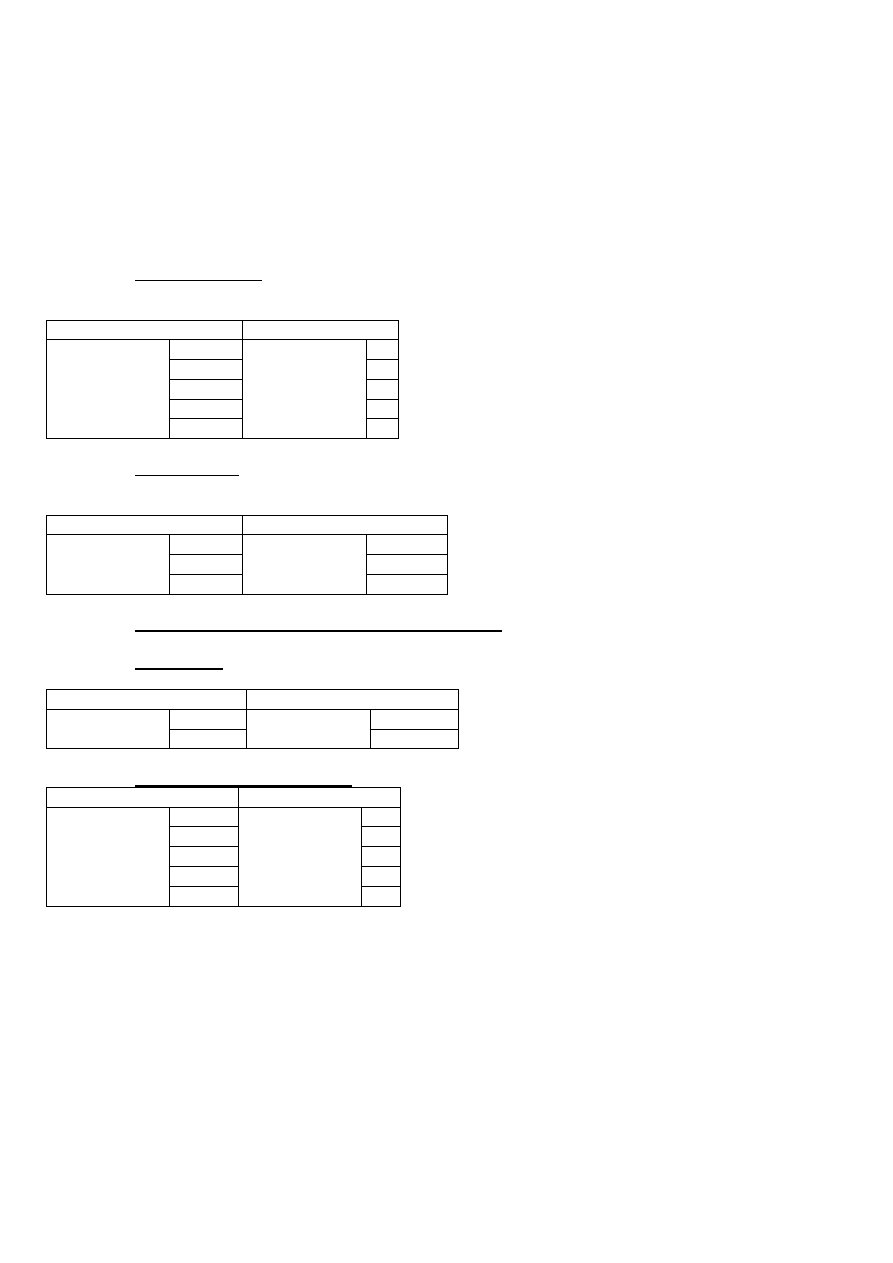
22



Sprawdzanie negatywne

– dla zdania znajdujemy następstwa fałszywe i wtedy choć jedynie z

pewnym prawdopodobieństwem, wnioskujemy o jego fałszywości jako racji.[NIEZAWODNE!!]



Wnioskowanie indukcyjne

– polega na tym, że na podstawie wielu przesłanek jednostkowych

stwierdzających, iż poszczególne zbadane przedmioty pewnego rodzaju mają określoną cechę,
dochodzi się do wniosku ogólnego stwierdzającego, że każdy przedmiot tego rodzaju taką cechę
posiada.



Indukcja enumeracyjna niezupełna – zbiór przesłanek jednostkowych( stwierdzających o
poszczególnych badanych przedmiotach, że posiadają pewną cechę) nie jest pełny[ZAWODNE!!]



Indukcja enumeracyjna zupełna - zbiór przesłanek jednostkowych (stwierdzających o
poszczególnych badanych przedmiotach, że posiadają pewną cechę) jest pełny[NIEZAWODNE!!]



Indukcja eliminacyjna

– rozwiązanie tą metodą odbywa się za pomocą kanonów.



Kanon zgodności – we wszystkich przesłankach powtarza się jeden element, a wnioski są takie
same(czyt. Przyczyną wniosków jest element powtarzający się)

Sfera przyczynowa

Sfera skutkowa

Występowanie
Zjawisk

ABCDE

Występowanie
Zjawiska

Z

1

BCDE

Z

1

ABDE

Z

1

ABCE

Z

1

ABCD

Z

1



Kanon różnicy – Wszystkie wnioski oprócz tego w, którego przesłankach nie ma jakiegoś
elementu, są takie same(czyt. Przyczyną wniosku jest element powtarzający się, którego nie ma
we wniosku który się nie powtarza)

Strefa przyczynowa

Strefa skutkowa

Występowanie
Zjawisk

ABCDE

Występowanie
Zjawiska

Z

1

ABDE

Z

1

ACDE

BRAK Z

1



Połączony kanon jednej różnicy i jednej zgodności – najpierw kanon jednej zgodności, później
jednej różnicy



Kanon reszt

– kanon ten formułuje myśl, że to, co pozostaje niewyjaśnione w sferze skutkowej,

jest wynikiem oddziaływania tego, co pozostaje niewyjaśnione w sferze przyczynowej

Strefa przyczynowa

Strefa skutkowa

Występowanie
Zjawisk

ABC

Występowanie
Zjawiska

Z

1

,Z

2

AB

Z

2

Wniosek: C jest przyczyną zjawiska Z

1



Kanon zmian towarzyszących

Sfera przyczynowa

Sfera skutkowa

Występowanie
Zjawisk

ABCD

Występowanie
Zjawiska

Z

1

A*BCD

Z

1

AB*CD

Z

1

*

ABC*D

Z

1

ABCD*

Z

1

Wniosek: B jest przyczyną Z

1

Występująca w schemacie gwiazdka oznacza zmianę stopnia oddziaływania określonego zjawiska
w sferze przyczynowej bądź zachodzenie zmian w zjawisku w sferze skutkowej



Wnioskowanie pr

zez analogię – jest rozumowaniem o charakterze nie dedukcyjnym. Od

szczegółowej przesłanki przechodzimy do szczegółowego wniosku



Z faktu, że przesłanki stwierdzają, iż każdy kolejny przedmiot określonego rodzaju posiada pewną
cechę wysnuwa się wniosek, że dalszy kolejny też będzie ją posiadać



Na podstawie szeregu przesłanek stwierdzających, że określony przedmiot posiada wiele cech,
które powodują, że należy on do szeregu klas przedmiotów wśród, których znajduje się klasa
poszukiwana

, wysnuwamy wniosek, że inny przedmiot, u którego stwierdzamy, że też posiada te

same cechy, które powodują, że należy do tych samych klas przedmiotów, wyjątkiem cechy
przesądzającej o przynależności do klasy poszukiwanej tę samą cechę również posiada(również
należy do klasy poszukiwanej)

23

Inne podziały wnioskowań
ZAWODNE i NIEZAWODNE

 Zawodne

(tłumaczenie, sprawdzanie, indukcję enumeracyjną niezupełną, indukcję statystyczną,

indukcję eliminacyjną, wnioskowanie z analogii)

 Niezawodne

(wnioskowanie sensu stricte, dowodzenie, indukcję enumeracyjną zupełną)

ZWYKŁE i Z PRZESŁANKAMI ENTYMEMATYCZNYMI



Zwykłe



Z przesłankami entymematycznymi – przesłanka, która nie jest przedstawiona we wnioskowaniu
bo uważa się ją za oczywistą.

Błędy we wnioskowaniach



Błąd materialny – polega na przyjęciu we wnioskowaniu fałszywej przesłanki



Błąd formalny – dotyczy tylko wnioskowań o charakterze dedukcyjnym i polega na oparciu się na
schemacie nie będącym prawem logicznym



Błąd stwierdzenia poprzednika w oparciu o następnik



Błąd zanegowania poprzednika – popełnia ten kto w oparciu o przesłankę(p→ q) i przesłankę ~p
błędnie wnioskuje, że prawdziwe jest zdanie ~q



Błąd fałszywego połączenia – na podstawie przesłanki stwierdzającej, że każda część przedmiotu
X ma własność W, wnioskujemy, że cały przedmiot X ma własność W

 B

łąd fałszywego podziału – na podstawie przesłanki stwierdzającej, że pewien zbiór ma określoną

własność, wnioskuje, że każdy element tego zbioru też ma tą własność



Błąd następstwa – polega na tym, że z faktu, że wydarzenie A poprzedza wydarzenie B
wysnuwam

y wniosek, że wydarzenie A jest przyczyną wydarzenia B.



Błąd wnioskowania z reguły na wyjątek



Błąd wnioskowania z wyjątku na regułę – popełnia ten kto nie rozpoznając, że chodzi o pewien
wyjątek, uznaje, że chodzi o regułę.



Błąd nieznajomości dowodzonej tezy – uzasadniający dowodzi nie tę tezę, którą miał
udowadniać



Błąd nieuzasadnienia przesłanki – polega na przyjęciu jakiś przesłanek bez wystarczającego
uzasadnienia



Błędne koło w dowodzeniu – polega na przyjęciu na przesłankę tego co ma być dowodzone



Błąd fałszywej analogi – polega na przyjęciu fałszywego założenia o związku między cechami
podobnych przedmiotów.

Rozdział X: Wnioskowanie statystyczne
Ogólna charakterystyka indukcji statystycznej
Indukcja statystyczna

jest odmianą wnioskowania niededukcyjnego zawodnego, lecz w przeciwieństwie

do pozostałych metod wnioskowania indukcja statystyczna umożliwia określenie prawdopodobieństwa
wniosku.(

badamy występowanie cech w zbiorowości dostępnej empirycznie).

-

Indukcja zupełna – czyli ta w której zbadaliśmy wszystkie przypadki jest szczególnym przypadkiem
wnioskowania dedukcyjnego

- Indukcja statystyczna

– czyli ta w której badamy losowo wybraną część zbiorowości

Badanie losowe

– istnieje wtedy gdy nie ma żadnej zależności pomiędzy cechą będącą podstawą poboru

j

ednostki do próby a cechą, która jest przedmiotem badania.



Każda jednostka zbiorowości generalnej musi mieć dodatnie prawdopodobieństwo dostania się do
próby.



Dla każdego zespołu jednostek zbiorowości można obliczyć prawdopodobieństwo dostania się do
próby

Badania dzielimy na badania jednoetapowe i wieloetapowe ze wzgl.

na to czy próbę pobieramy od razu czy

w kolejnych losowaniach.
Indukcja statystyczna musi zawierać:

1.

Przesłanka = koniunkcja twierdzeń szczegółowych

2.

Wniosek = twierdzenie uogólniające

3.

Wymóg losowości

4.

Prawdopodobieństwo prawdziwości uogólnienia

BADANIE SKŁADA SIĘ Z CZTERECH CZĘŚCI:

Badanie

Określenie badanej cechy

Zidentyfikowanie tego co jest jednostką badanej zbiorowości

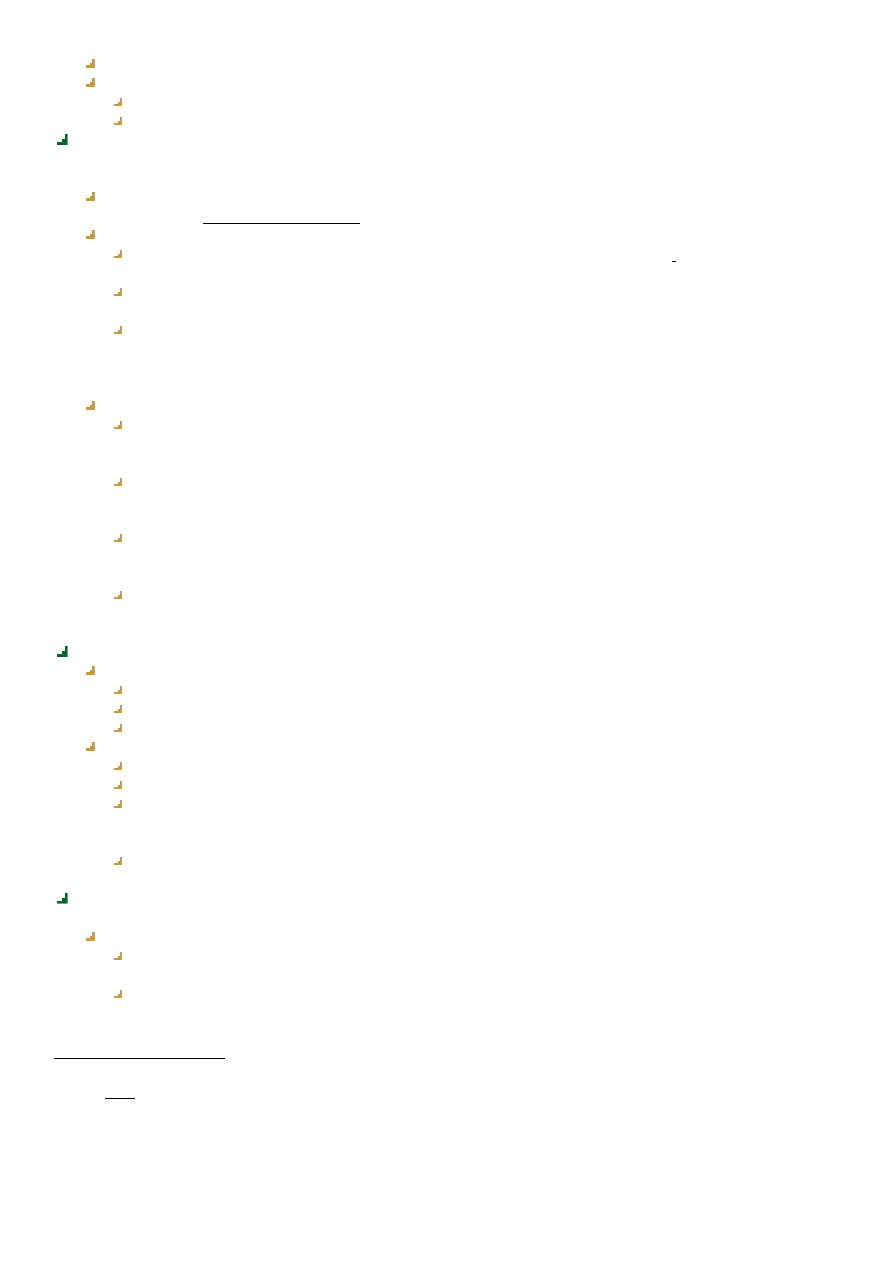
24

Określenie zbiorowości

Przyjęcie pewnej konwencji co do badanej cechy

C

echy ilościowe – czyli takie które się zlicza

Cechy jakościowe – czyli takie które się mierzy

Pomiar

– przyporządkowanie jednostkom zbiorowości statystycznej wielkości liczbowych dokonane z

uwzględnieniem poziomu badanej cechy u tej zbiorowości. Cechą wspólną pomiarów jest to, że ich
efektem jest wyznaczenie liczb

Przeprowadzamy obserwację badanej zbiorowości pod kątem badanej cechy. Wynikiem tego
pomiaru jest

materiał statystyczny.[dokładny opis str. 207 dół].

Warunki

, które powinien spełnić pomiar statystyczny

Warunek równości – wtedy i tylko wtedy, gdy jednostkom zbiorowości, u których badana cecha
występuje w równym natężeniu, przypisujemy równe wielkości liczbowe.(„równy – różny”)

Warunek porządku – zakłada utrzymanie pomiędzy wynikami pomiaru relacji „większy –
mniejszy” zachodzącej pod wzgl. badanej cechy pomiędzy jednostkami zbiorowości

Warunek dodawania

– wtedy, gdy jesteśmy w stanie niearbitralnie określić naturalny stan

zerowy występowania badanej cechy oraz potrafimy uporządkować zbiorowość ze wzgl. na tę
cechę w taki sposób by znalazła odbicie w tym uporządkowaniu odległość elementów od siebie
oraz odległość od naturalnego początku układu

Skale pomiarowe

Skala nominalna

– sprowadza się do przeprowadzenia podziału jednostek zbiorowości ze

względu na mierzoną cechę i następnie na przypisaniu wszystkim jednostkom włączonym do
jednego członu podziału takiej samej liczby(„równy – różny”)

Skala porządkowa – polega na przypisaniu elementom zbiorowości określonych rang ze wzgl.
na posiadaną przez nie cechę w ten sposób aby zachowana została relacja „większy –
mniejszy”

Skala podziałowa – polega na przyjęciu celów pomiaru określonych jednostek pozwalających
na określenie dystansu pomiędzy jednostkami zbiorowości pod wzgl. mierzonej cechy.(brak
punktu zer

owego => możliwe działania tylko dodawanie i odejmowanie).

Skala stosunkowa

– posiada wszystkie własności omówionych skal a ponadto dysponuje

określeniem bezwzględnej wartości zera(tzn. nieumownej) mierzonej cechy(wszystkie pomiary
centymetr

– gram - sekunda).

Opis statystyczny

Opis polega na:

Pogrupowanie i zliczenie jednostek
Przeprowadzenie klasyfikacji

Budowie tablic, wykresów oraz policzeniu miar statystycznych

Metodami opisu są

Przedstawienie wyników pomiarów w postaci szeregów statystycznych uporządkowanych

Przedstawienie zbiorowości statystycznej w postaci tablic i wykresów

Obliczenie miar statystycznych „przeciętności”, takich jak średnie, miary pozycyjne, różnego
typu wskaźniki dla cech jakościowych, różnego typu wskaźniki i miary tendencji występujących
w tendencjach czasowych

Obliczenie miar zróżnicowania jednostek badanej zbiorowości pod względem badanych cech,
takich jak odchylenie standardowe, współczynniki zmienności, skośności pułapu i inne.

Wnioskowanie

– tu zostaje określone prawdopodobieństwo z jakim można odnieść wynik do całej

zbiorowości.

Wnioskowanie statystyczne przebiega według jednego z dwóch podstawowych schematów:

Estymacji

– oszacowania badanego parametru w całej zbiorowości na podstawie badania

pobranej z tej zbiorowości próby

Weryfikacji

– sprawdzenia hipotezy dotyczącej całej zbiorowości na podstawie badania

pobranej z tej zbiorowości próby.

Prawdopodobieństwo

1. definicja klasyczna(aprioryczna)

–

Gdzie m reprezentuje te przypadki które sprzyjają zajściu zdarzenia, a n liczbę wszystkich
możliwych przypadków

2.

Częściowa aposterioryczna definicja prawdopodobieństwa – zakładała że
prawdopodobieństwo można wyznaczyć tylko w wyniku badanych zdarzeń empirycznych

P(A)=

m
n

25

polegających na badaniu częstości ich występowania. X i Y – zdarzenia (X <=> kiedy jest Y) m-
częstość występowania X, n częstość występowania y

P(X)= lim (

m

)

n

n→∞

3.

Prawdopodobieństwo subiektywne – charakteryzuje się tym, że jeśli mamy dwa zdarzenia co do
których nie wiemy, które jest bardziej prawdopodobne to przypisujemy im tę samą wartość

4.

Prawdopodobieństwo logiczne - odnosi się nie do zdarzeń lecz do zdań (str. 216)

Rozdział XI: Przekazywanie myśli
Pytania i odpowiedzi
Pytanie składa się:



Partykuły pytanej(niekoniecznie)



Zdanie w sensie logicznym



Znak zapytania

Logika pytań = Logika erotetyczna
Pytania dzielimy na:
O

twarte i zamknięte:



Pytania zamknięte – to te w których sugerujemy schemat odpowiedzi (np. Ilu jest posłów sejmie
RP? W sejmie RP jest n Posłów)

 Pytania otwarte -

to te, w których nie sugerujemy schematu odpowiedzi.

Pytania rozstrzygnięcia i dopełnienia



Pytania rozstrzygnięcia – to t, na które odpowiadamy tak lub nie(zawierające partykułę „czy” lub
dające się sprowadzić do schematu(„pożyczysz mi 1000 złotych?”)), mogą to być też zdanie
wieloczłonowe(tzn. możliwe jest, że na zadane pytanie jest jedna, dwie lub więcej odpowiedzi)

 D

opełnienia – cała reszta

Osnowa pytania

– schemat odpowiedzi będący funkcją zdaniową(sugerowany w pytaniu?)

Zakres niewiadomej pytania

– zakres możliwych odpowiedzi(prawdziwych lub nie)

Pozytywne założenie pytania – kiedy wśród odpowiedzi znajduje się przynajmniej jedno prawdziwe
zdanie.
Negatywne założenie pytania – zakładamy, że w zbiorze możliwych odpowiedzi znajduje się przynajmniej
jedno zdanie fałszywe.
P

ytanie niewłaściwie postawione – kiedy pozytywne lub negatywne założenie jest źle postawione.

ODPOWIEDZI

WŁAŚCIWE I NIEWŁAŚCIWE



Odpowiedź właściwa – wywodząca się z niewiadomej pytania



Odpowiedź niewłaściwa – wywodząca się z poza niewiadomej pytania

CAŁKOWITE WPROST, CAŁKOWITE NIEWPROST i CZĘŚCIOWE



Odpowiedź całkowita wprost – Odpowiedź właściwa wiernie odzwierciedlająca osnowie
pytania(wywodząca się z zakresu niewiadomej pytania)



Odpowiedź całkowite niewprost – Odpowiedź nie zgodna z schematem osnowy pytania(z której
jednak możemy jednoznacznie wywnioskować prawdziwą odpowiedź)



Odpowiedź częściowa – eliminuje tylko część z możliwych odpowiedzi(nie zgodna z schematem
osnowy pytania)

Metody przesłuchania:

-

Metoda swobodnej relacji

-

Metoda przesłuchiwania wyłącznie przez zadawanie pytań

-

Metoda mieszana

PODZIAŁY PYTAŃ(nie uznawanych na Sali sądowej)



Pytania sugerowane

– , czyli takie, w których jest zawarta proponowana odpowiedź



Pytania podchwytliwe

– , czyli takie, że intencją pytającego jest skłonić pytanego do odpowiedzi

sprzecznej z tym co wcześniej powiedział, lub czegoś co pragnie zataić.



Pytania nieistotne

– Pytania nie dotyczące sprawy.

26

Perswazja i dyskusja:
(Greckie)Zasady retoryki:

Ograniczoność – wypowiedź ma być traktowana jako ograniczona całość(wymagany wewnętrzny
porządek)

Stosowność – niezbędne jest odpowiednie dobranie środków retorycznych

Funkcjonalność – funkcją wypowiedzi jest przekonanie słuchacza

Dyskusja(przekonywanie się dwóch lub więcej stron do swoich racji, w formie wymiany zdań)powinna być:

Klarowna

– dostosowanie „języka wypowiedzi”, tak żeby był zrozumiały dla wszystkich członków

dyskusji.

Merytoryczna

– wymaganie dokładnego określenia przedmiotu dyskusji.

Konkluzywność - wymaganie dokładnego określenia założeń dyskusji

Logomachia

– jałowy spór słowny

Erystetyka

– umiejętność prowadzenia sporów.

CHWYTY ESTETYCZNE:

Argumentum ex concesso

– odznacza się dostosowaniem prezentowanej argumentacji do

człowieka, z którym toczy się spór. Próbuje się wysnuć wnioski dla własnej tezy z przesłanek
przeciwnika.

Argumentum ad personam

– zamiast dyskutować atakuje się personalnie przeciwnika

Argumentum ad baculum

– groźba użycia przemocy

Argumentum ad crumenam

– punktem odniesienia jest tu interes zgromadzonych

Argumentum ad misericodium

– zamiast do racji merytorycznych, następuje odwołanie się do

czynników mających wzbudzić litość.

Argumentum ad verecundiam

– argument odwołujący się do nieścisłości(odwołanie się do

autorytetów)

Argumentum ad venitatem

– odwołuje się do różności słuchaczy. (komplementy)

Argumentum ad populum

– słuchaczom mówi się nie to co odpowiada rzeczywistości lecz to co

odpowiada ich pragnieniom.

Błędy w przekazywaniu myśli:



Błąd ekwiwokacji – użycie słowa wieloznacznego nie wyjaśniając o które znaczenie chodzi



Błąd czterech terminów – k



Błąd figuralnego myślenia – polega na dosłownym rozumowaniu znaczenie wyrazów, użytych
przenośnie

WIELOZNACZNOŚĆ WYRAŻEŃ



Wyrażenia okazjonalnego – czlyli złego zrozumienia wyrażenia niemającego stałego zbioru
desygnatów(np. wyrażenia z „ja” itp.)



Błąd amfibologii – gdzie źródłem wieloznaczności wyrażenia jest jego struktura



Posługiwania się wyrażeniami nieostrymi(np. wysoki człowiek, szczegółowa analiza rozdział III)



Niedopowiedzenie kwantyfikacji

– kiedy w naszej wypowiedzi nie zostanie określone, czy dotyczy

ona niektórych czy wszystkich elementów danej klasy



Niedopowiedzenie relatywizacji

– wiąże się z brakiem wskazania punktu odniesienia

Rozdział XII: Wypowiedzi oceniające, normatywne i modalne
Wypowiedzi oceniające
Wypowiedź oceniająca – polega na określeniu relacji pomiędzy oceniającym stanem rzeczy a kryterium
(formułowanych na podstawie kryteriów uznawanych przez oceniającego za słuszne). Zdarza się również,
że wypowiedź oceniająca ma charakter porównawczy.
Oceny instrumentalne

– wtedy kiedy orzekamy o przydatności czegoś jako środka do osiągnięcia

zamierzonego celu
Wypowiedzi optatywne

– zawierające ocenę stanu rzeczy przyszłego.

Normy postępowania
Norma

– wypowiedź zawierająca wzór postępowania, którego twórca normy żąda w przyszłości, od

osoby/osób gdy znajdą się w określonej sytuacji.
Dyrektywa techniczna

– wskazująca sposób postępowania prowadzący do osiągnięcia danego skutku.

Normodawca

– twórca/y normy

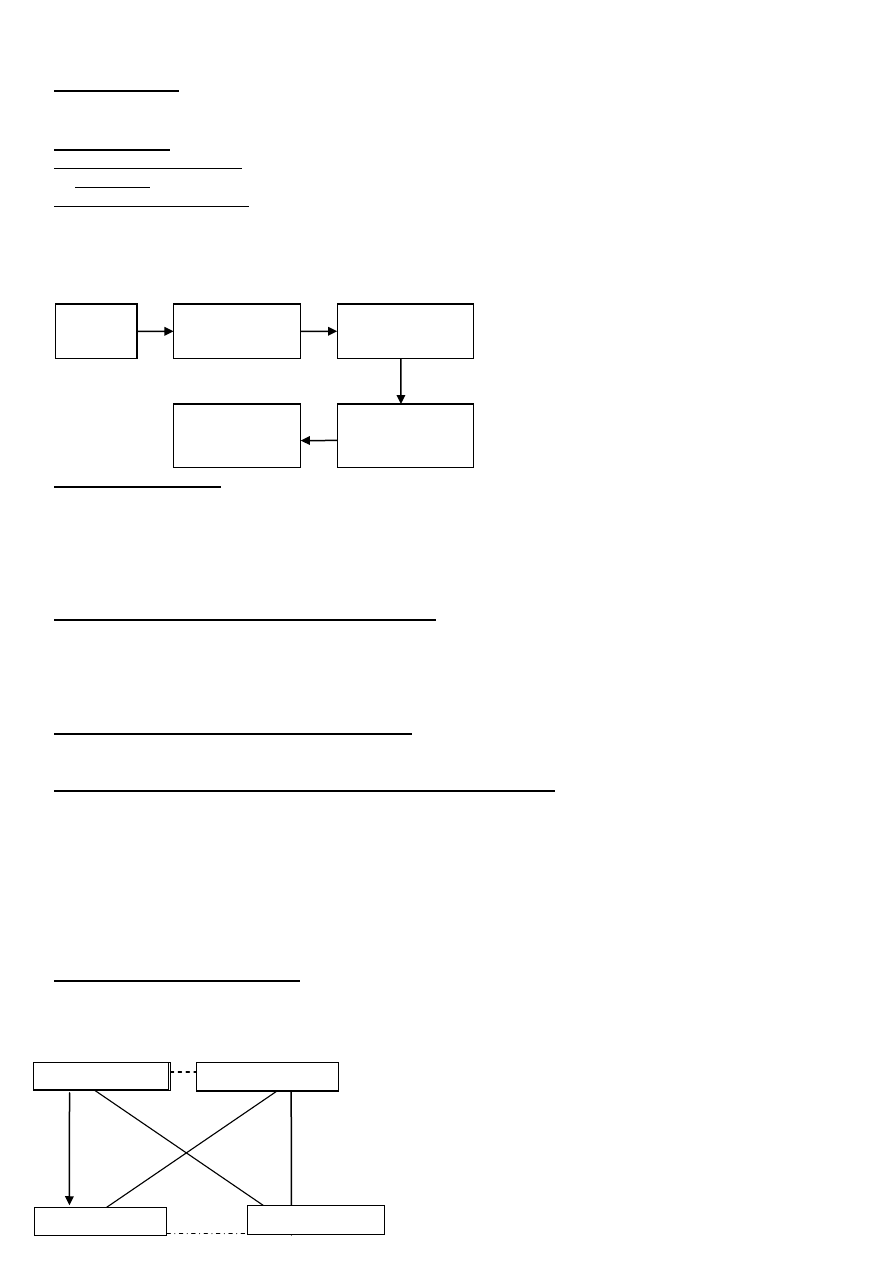
27

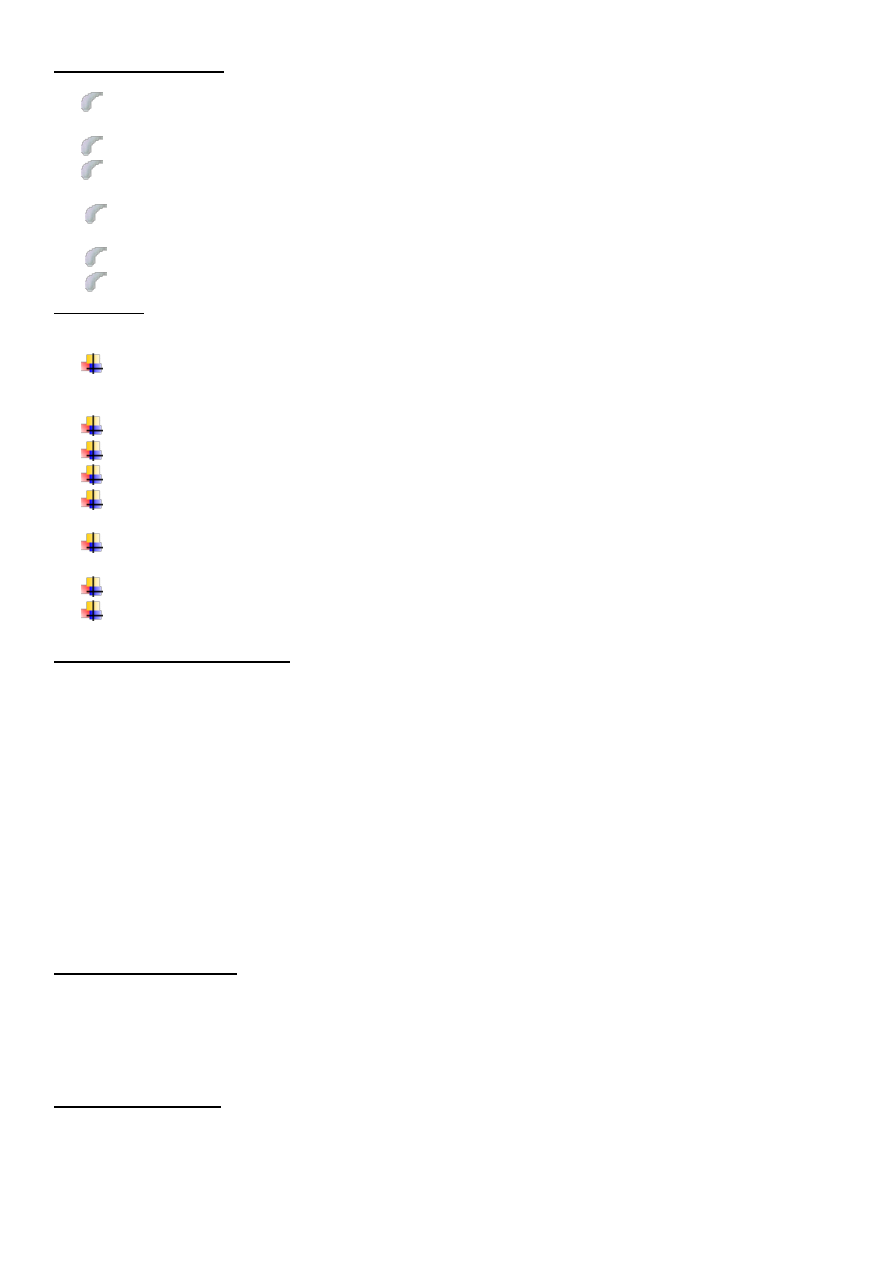
Musi być tak że ~Z

Może być tak, że Z

Musi być tak, że Z

Może być tak, że ~Z

Adresat normy

– osoba do której jest skierowana norma

Budowa normy:



Trójelementowa(hipoteza – dyspozycja – sankcja)



Koncepcja norm sprzężonych(norma sankcjonowana, norma sankcjonująca)

Hipoteza normy

– określa warunki faktyczne w jakich norma może być zastosowana wobec adresata.

Zakres stosowania normy

– zbiór wszystkich sytuacji w których norma może być zastosowana.

W dyspozycji

– określone jest zachowanie powinne wymagane od adresata

Zakres normowania normy

– zbiór zachowań adresatów normy, które ta norma determinuje.

Norma prawna

– to taka norma postępowania, która jest najmniejszym elementem stosowania prawa

Przepis normatywny(prawny)

– to jednostka systematyki tekstu prawnego, Jest on zdaniem w sensie

gramatycznym. W tym sensie przepis prawny jest obiektem empirycznym, który można zobaczyć i
p[przeczytać(informacja o ustanowionych przez prawodawcę normach).
Proces odczytywania normy:

Wypowiedzi modalne
Wypowiedź modalna – to takie zdanie opisowe w sensie gramatycznym w którym występuje funktor
modalny.
Funktory modalne:



„musi” za pomocą, którego budowane są zdania apodyktyczne



„może” za pomocą, którego budowane są zdania problematyczne.

Funktor modalny jest jednoargumentowy(jego argumentem jest zdanie w sensie logicznym)
Wyróżniamy cztery typy wypowiedzi modalnych:

1.

musi być tak, że Z

2.

musi być tak, że ~Z

3.

może być tak, że Z

4.

może być tak że nie Z

gdzie Z jest zdaniem w sensie logicznym i argumentem funktora modalnego
Interpretacja logiczna wypowiedzi modalnych
Interpretacja logiczna wypowiedzi modalnych odwołuje się do – jako do stosowanego kryterium –
całokształtu wiedzy osoby przeprowadzającej interpretację tej wypowiedzi.
Zdanie „Z” w stosunku do wiedzy „W” może pozostawać w stosunku:

1.

Zdanie Z jest elementem zbioru zdań W albo w zbiorze tym znajduje się inne zdani(e/a), z których
wynika zdanie Z. Inte

rpretator wie, że Z jest prawdą.

2.

W zbiorze zdań „W” znajduje się zdanie sprzeczne z „Z” albo w zbiorze tym znajduje się inne
zdani(e/a), z których wynika, że zdanie sprzeczne do Z(tzn. zdanie ~Z). Interpretator wie, że
zdanie Z jest fałszywe.

3. W zbiorze zda

ń W nie ma ani zdania Z ani ~Z, a także nie ma zdań z których wynikałoby zdanie Z

lub ~Z. Interpretator nie wie nic na temat zadnia Z.

Na podstawie wyróżnionych trzech powyższych przypadków, w interpretacji logicznej przyjmuje się
następujące zasady przypisywania wartości logicznej prawdy wypowiedziom modalnym:
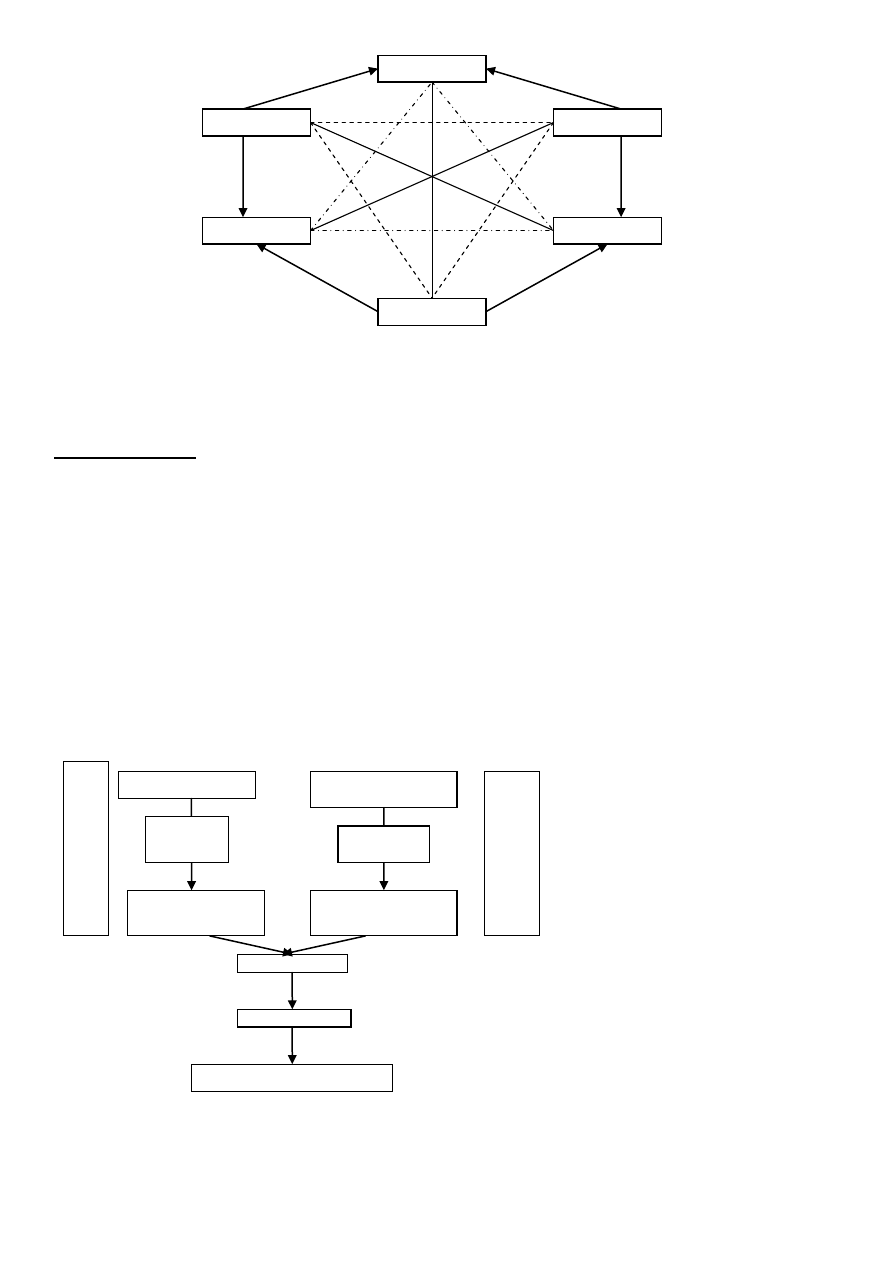
MOŻLIWOŚĆ JEDNOSTRONNA

1.

musi być tak, że Z(prawdziwe w sytuacji 1)

2.

musi być tak, że ~Z(prawdziwe w sytuacji 2)

3.

może być tak, że Z(prawdziwe w sytuacji ~2 tzn. w sytuacjach 1 i 3)

4.

może być tak że ~Z(prawdziwe w sytuacji ~1 tzn. w sytuacjach 2 i 3)

a)

strzałki = wynikanie

b)

linie = sprzeczność

c)

linia przerywana = zdania przeczące

d) linia przerywana z kropkami = zdania podprzeciwne

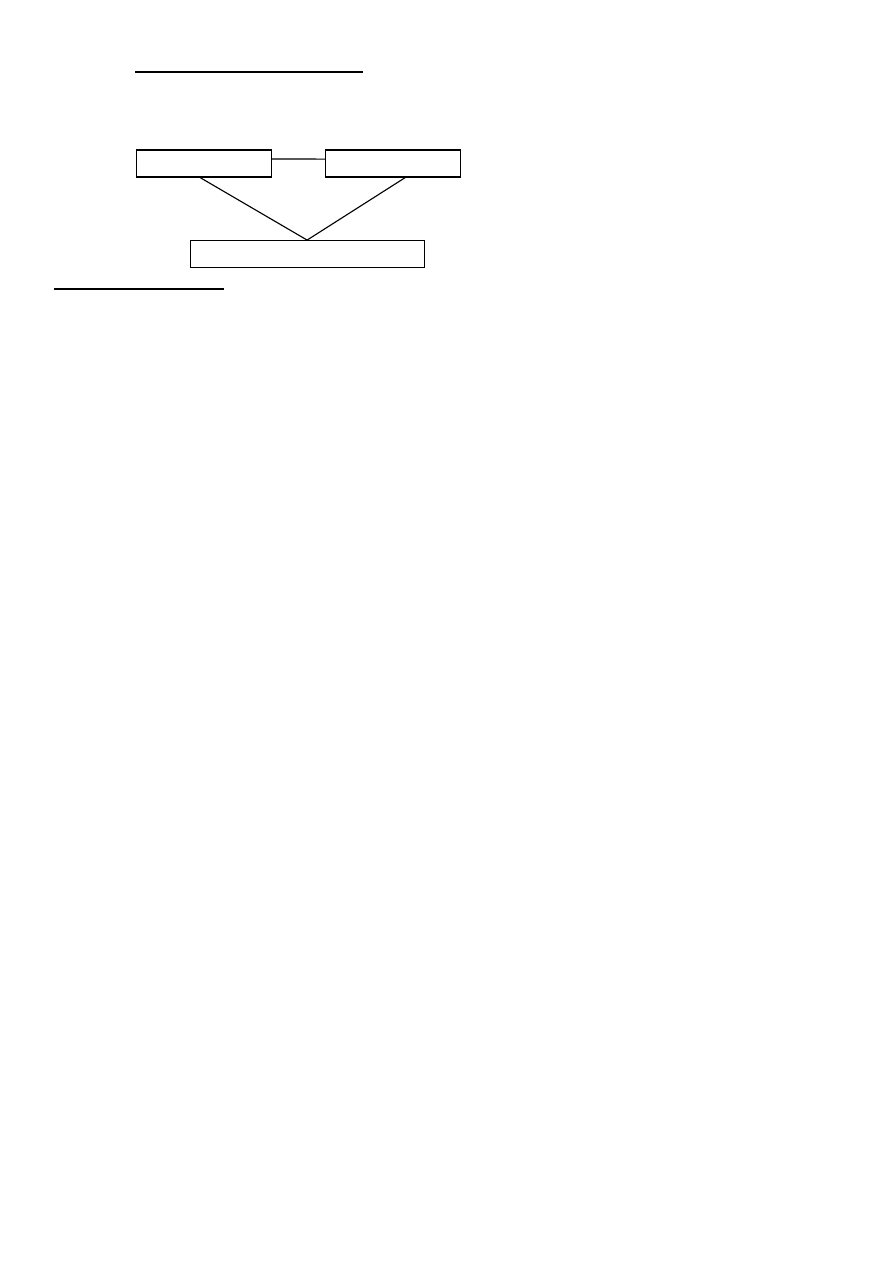
Normodawca

Kodowanie norm w
języku aktów
prawnych(legislacja)

Kanał informacyjny(

Odkodowywanie norm z
przepisów(wykładnia
prawa)

Adresat normy

28

MOŻLIWOŚĆ DWUSTRONNA

1.

musi być tak, że Z(prawdziwe w sytuacji 1)

2.

musi być tak, że ~Z(prawdziwe w sytuacji 2)

3.

może być tak, że Z i może być tak że nie Z(prawdziwe w sytuacji 3)

Linia łączy zdania przeciwne

Interpretacja tetyczna
Interpretacji tetycznej podlegają tylko te wypowiedzi które spełniają warunki;



Orzekają o osobach



Orzekają o czynach osób

W związku z tym wyróżniamy tu cztery sytuacje:



Musi być tak że x czyni c



Musi być tak że x czyni ~c



Może być tak że x czyni c



Może być tak że x czyni ~c

Dokonując interpretacji tetycznej dysponujemy:
1.

Wypowiedzią modalną

2.

Zbiorem N norm postępowania o uzasadnieniu tetycznym

Porównanie tych informacji może doprowadzić do jednej z 5 sytuacji:
1.

Czyn c osoby x jest nakazany przez normę n ze zbioru N

2. Czy

n c osoby x jest zakazany przez normę n ze zbioru N

2.a. Czyn c osoby x je

st objęty wprost zakazem określonym przez normę n.

2.b.

działanie c osoby x jest sprzeczne z nakazem zawartym w normie n

2.c.

działanie c osoby x jest przeciwne do działania nakazanego przez normę n

3.

Norma n ze zbioru N stwierdza, że czyn c osoby x nie jest nakazany(czyn taki nazywamy
fakultatywnym)

4.

Norma n ze zbioru N stwierdza, że czyn c osoby x nie jest zakazany(czyn taki nazywamy
jednostronnie dozwolonym)

5.

Żadna z norm zbioru N nie orzeka o czyni c osoby x.

Posługując się opisaną wyżej typologią czynów, czynów których orzeka norma opracowano konwencję,
stosowanie do której będziemy przypisywali wypowiedziom modalnym wartości logiczne:

I.

„x musi czynić c” – czyn nakazany(Nncx = ze wzgl. na normę n czyn c osoby x jest

nakazany)(prawdziwy w sytuacji 1)

II.

„x musi nie czynić c” – czyn zakazany(Zncx)(prawdziwy w sytuacji 2)

III.

„x może czynić c” – czyn dozwolony(Dncx)(prawdziwy w sytuacjach ~2 czyli 1,4,5)

IV.

„x może czynić nie c ” – czyn fakultatywny(Fncx)(prawdziwy w sytuacjach ~1 czyli 2,3,5)

V.

jeżeli zarazem prawdziwe jest „x może czynić c” i „x może czynić nie c” – czyn

indyferentny(Incx)(prawdziwy tylko sytuacja 5 )

VI.

jeżeli jest „x musi czynić c” albo „x musi nie czynić c” – czyn jest przedmiotem

Obowiązku(Oncx)(Prawdziwy kiedy Oncx ≡ Nncx _|_ Zncx).

musi być tak, że Z

musi być tak, że ~Z

może być tak, że Z i może być tak że ~ Z

29

s

trzałka = wynikanie

linia kreska

– kropka = podprzeciwne

przerywana linia = przeciwne
linia = sprzeczne

Rozdział XIII: Logika w procesie stosowania prawa
Struktura procesu
Przez Stosowanie prawa(I)

określa się czynności kompetentnych organów państwowych, w trakcie

których następuje ustalenie faktów prawnych i przyporządkowanie im odpowiednich konsekwencji na
podstawie obowiązujących norm prawnych.
Stosowanie prawa(II)

– aktywność organów państwa, organów osób prawnych lub innych podmiotów

upoważnionych do stosowania prawa. Aktywność polega na:



Wiążącym ustaleniu praw lub obowiązków osób albo stanu prawnego w decyzji stosowania prawa.



Wykorzystaniu kompetencji do działań nie polegających na wydaniu decyzji stosowania prawa



Wykorzystaniu uprawnień i spełnieniu obowiązków nałożonych przez normy prawne

Proces stosowania prawa

1.

Analiza okoliczności stanu faktycznego

2.

Wybór odpowiedniego przepisu

3. Interpretacja przepisu w celu uzyskania normy prawnej
4.

Ustalenie jej mocy obowiązującej

5.

Podjęcie decyzji

6. Wydanie aktu za

wierającego decyzję

Oncx

Zncx

Nncx

Dncx

Incx

Fncx

Empiria

Stwierdzenie Zaistnienia

określonego faktu

Przepisy prawne

Norm Prawna

Subsumcja

Podjęcie decyzji

Wydanie aktu zawierającego decyzję

Reguły
dowodowe

Dyrektywy

wykładni

U

st

al

en

ia

f

ak

ty

cz

n

e

U

st

al

en

ia

n

o

rma
ty

w

n

e

30

Fakty:



Fakty Wyróżnione opisowo – sprowadza się do wypowiedzi „x istnieje w czasie t i przestrzeni p”



Fakt wyróżniony oceniająco – W pierwszym etapie stwierdza się Istnienie czegoś, co jest
przedmiotem o

ceny, a następnie przedmiot ten jest odpowiednio wartościowany. Ocena ta może

występować bądź jako szacowanie wielkości lub ilości, bądź jako emocjonalne ustosunkowanie się.

Ocena dowodów:



Teoria swobodnej oceny dowodu

– uznanie przedstawionych dowodów za wiarygodne i

pozwalające ustalić prawdziwy obraz faktu należy do organu stosującego prawo



Teoria

związanej oceny dowodów – z mocy samego prawa istnieją dowody bardziej i mniej

wiarygodne

Domniemanie

– jest wnioskowaniem, który występuje następujący schemat rozumowania. Jeżeli

zdarzenie A bardzo często łączy się ze zdarzeniem B to pojawienie się konkretnego „a” należącego do
zbioru zdarzeń A łączy się najprawdopodobniej z zdarzeniem „b”, a służy przerzuceniem ciężaru dowodu
na drugą stronę.
Rozdział XIV: Wykładnia prawa
Pojęcie wykładni prawa
Wykładni prawa – proces ustalania właściwego znaczenia przepisów prawnych.
Zakres wykładni prawa możemy uznać jako:

 Koncepcja klasyfikacyjna -

Wykładni wykonuje się tylko tyle, o ile wymagają to niejasności tekstu.

 Koncepcja derywacyjna

– wykładni dokonuje się w każdym przypadku ustalania normy prawnej

Potrzeba przeprowadzenia wykładni wynika z(koncepcja klasyfikacyjna):

Niejednoznaczności języka naturalnego i prawnego;

Błędów popełnionych przez ustawodawcę;

Świadomie wprowadzonych przez ustawodawcę niejednoznaczności i nieostrości
wypowiedzi normatywnych;

Ze „starzenia” się regulacji normatywnych

Potrzeba przeprowadzenia wykładni wynika z(koncepcja derywacyjna):

Wynika z rozróżnienia normy prawnej i przepisu prawnego=> jest zawsze konieczna

Podpunkty z koncepcji klasyfikacyjnej

Teorie wykładni prawa

a)

Teoria wykładni statystycznej(subiektywna) – wraz z ustanowienie przepisu ustawodawca nadaje

mu określone znaczenie. Tak długo jak przepis formalnie funkcjonuje istnieje wraz z nim jego znaczenie.
Nie powinno się tego znaczenia swobodnie modyfikować. Tj. do ustalenia normy z przepisu potrzebna
nam jest wiedza o celach, wiedzy, przesłanek historycznych ustawodawcy historycznego.

b)

Teoria wykładni statystycznej(obiektywna) – Znaczenie przepisów prawnych nie powinno być

wiązane wyłącznie z wolą ustawodawcy historycznego, ponieważ prowadziłoby to, wbrew naturalnej
dynamice procesów społecznych. Wraz z wszelkimi zmianami w społeczeństwie w języku stare przepisy
powinny mieć nadawaną nową treść dostosowaną do współczesnych potrzeb(a nie ustawodawcy sprzed
wieku, który ustanowił daną ustawę).

c)

Teoria wykładni „aktualnego ustawodawcy” – jest ona pewną modyfikacją teorii wykładni

dynamicznej. Twierdzi ona, że jednoznaczne przyjęcie teorii dynamicznej doprowadziłoby do nadmiernej
dowolności w interpretacji prawa. Należy, więc posłużyć się w interpretacji wiedzą o rzeczywistości,
preferencjami aksjologicznymi oraz celami politycznymi ustawodawcy czynnego w momencie interpretacji

Założenie racjonalności ustawodawcy
Założenie racjonalności jest fundamentalną przesłanką metodologiczną tzw. Interpretacji humanistycznej:



Dzieło kulturowe jest kreacją człowieka, z którym interpretator dzieli podstawowe właściwości
fizyczne i duchowe a zatem jest w sta

nie go zrozumieć.



Twórca dzieła jest istotą racjonalną, tj. dokonuje wyborów celu i adekwatnych do ich osiągnięcia
środków zgodnie z posiadaną przez siebie wiedzą o rzeczywistości, kierują c się przy tym
niesprzecznym systemem wartości.



Rekonstrukcja prze

z interpretatora tej wiedzy i systemu wartości pozwala zrozumieć sens dzieła

kulturowego, będącego przedmiotem dociekań.

31

Rodzaje wykładni prawa
1. Pierwszą typologią jest zróżnicowanie ze względu na podmiot jej dokonujący. Według tego

kryterium występuje, zatem:
a. Wykładnia autentyczna – dokonywana jest ona przez ten podmiot, który przepis

ustanowił.(Zasięg i moc obowiązywanie takiej interpretacji jest równy zasięgowi i mocy wynikającej
z rodzaju interpretowanego aktu).

b. Wykładnia legalna – dokonywana jest przez uprawniony do tego organ państwa. Wykładnia prawa

delegowana

– kiedy uprawnienie do wykładni przepisu jest zawarte w samym przepisie.

c. Wykładnia operatywna – jest to rodzaj wykładni podejmowany przez organy stosowania prawa,

dokonywać jej mogą wszelki organy władzy państwowej. Szczególne znaczenie ma tu jednak
wykładnia sądowa. Np. wykładnia Sądu Najwyższego może przyjmować postać:

I.

Sąd najwyższy może rozpoznawać skargi kasacyjne wnoszone przez strony do orzeczeń sądu
drugiej instancji. W przypadku stwierdze

nia zasadności kasacji SN działający zwykle w składzie

trzyosobowym uchyla orzeczenie sądu drugiej instancji. Po przekazaniu powrotem do
odpowiedniego sądu jest ten sad związany wykładnią SN.

II.

Sąd najwyższy może podejmować uchwały jeżeli uzna, że celowe jest wyjaśnienie przepisów

prawnych budzących wątpliwości w praktyce lub których stosowanie wywołało rozbieżność w
orzecznictwie. Nie są to uchwały dotyczące bezpośrednio konkretnych spraw. Do ich podjęcia
dochodzi na wniosek

określonego organu państwa. Takie uchwały zapadają przy udziale &

sędziów w składzie całej izby sądu najwyższego, połączonych izb lub w pełnym składzie SN.

III.

Drugi typ uchwał SN może podejmować w następstwie przedstawienia mu do rozstrzygnięcia

tzw. Zagadnienia prawnego

budzącego poważne wątpliwości w konkretnej sprawie.

IV.

Uchwały 7-osobowych składów SN zapadających w trybie określonym w punktach II i III mogą

uzyskać moc Zasad prawnych, jeżeli taki 7-osobowy skład tak postanowi. W przypadku uchwał
całej izby dzieje się tak automatycznie. Taka wykładnia wiąże też inne składy orzekające SN.

d. Wykładnia doktrynalna – wykładni może dokonywać każdy na własny użytek, nie ma jednak ona

dla nikogo mocy wiążącej.

2. Ze względu na sposób dokonywania wykładni

a. Wykładnia językowa - Polega na dokonywaniu interpretacji przepisów prawnych przy

wykorzystywaniu reguł znaczeniowych i konstrukcyjnych języka prawnego i naturalnego, reguł
poprawnego myślenia i reguł logiki prawnej.

b. Wykładnia systemowa – Polega na ustaleniu rzeczywistego znaczenia przepisów ze względu na

ich usytuowanie w systematyce wewnętrznej systemu prawa lub zasady danej gałęzi prawa..

c. Wykładnia funkcjonalna – Ustalenie znaczenia przepisu zgodnie z celem, jaki chciał osiągnąć

ustawodawca stanowiąc ten przepis.

d. Wykładnia porównawcza – Polega na ustaleniu znaczenia przepisu przez porównanie go z

innymi podobnymi przepisami o ustalonym znaczeniu

I.

Układ synchroniczny – porównanie z przepisami innych krajów

II.

Układ diachroniczny – porównanie z przepisami niegdyś istniejącymi

3. Ze względu na wyniki wykładni

a. Wykładnia literalna(dosłowna) – ustalona ze względu na użycie reguł znaczeniowych i

konstrukcyjnych języka.

b. Wykładnia rozszerzająca – polega na porównaniu wyniku wykładni językowej i systemowej lub

celowościowej i przyjęciu szerszego znaczenia przepisu niż wynikałoby to z przepisu.

c. Wykładnia zwężająca – polega na porównaniu wy6ników wykładni literalnej i celowościowej lub

systematycznej i przyjęciu węższego znaczenia przepisu niż wynikałoby to z wykładni literalnej.

Zasada niesprzeczności norm i reguły kolizyjne
Rodzaje sprzeczności norm;
1.

Sprzeczności logiczne występuje, gdy:
1.1.

Jedna norma nakazuje podmiotowi w danych warunkach coś uczynić druga zaś zakazuje

1.2.

Jedna norma nakazuje podmiotowi w danych warunkach coś uczynić druga zaś dozwala to
uczynić(problem powstaje gdy adresat nie skorzysta z dozwolenia)

1.3.

Jedna norma zakazuje podmiotowi w danych warunkach coś uczynić druga zaś dozwala to uczynić

2.

Przeciwieństwa logiczne – polegają na tym, że dwie lub więcej norm nakazuje danemu adresatowi
różnego rodzaju zachowania, które są niemożliwe do jednoczesnego zrealizowania.

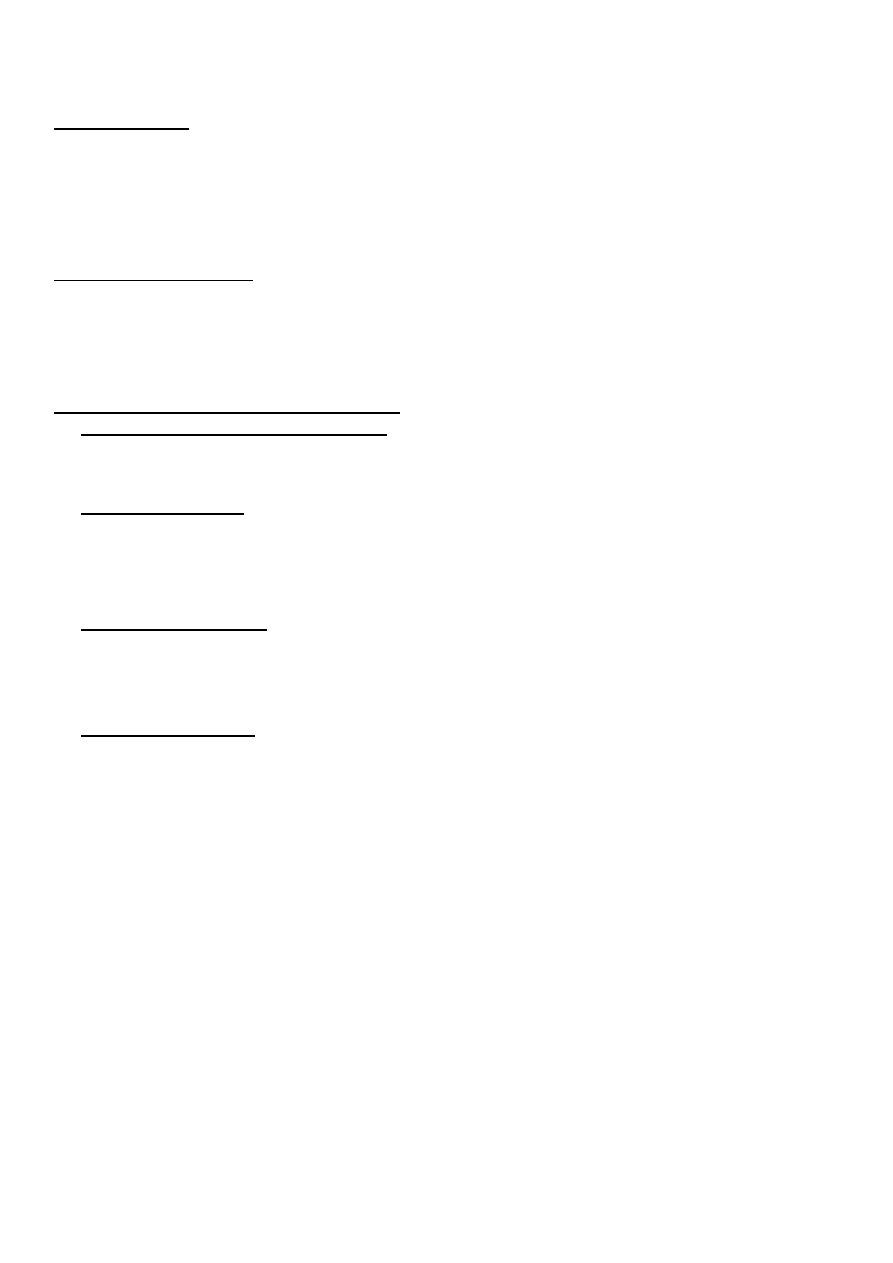
32

3.

Niezgodności prakseologiczne – polegają na tym, że zachowanie zgodne z jedną normą(lub skutek
takiego zachowania) unicestwia całkowicie lub w części skutek zachowania zgodnego z drugą normą

Reguły kolizyjne:
1.

Reguła kolizyjna porządku hierarchicznego – norma wyżej usytuowana w hierarchii norm uchyla
normę niższego rzędu.

2.

Reguła kolizyjna porządku czasowego – norm późniejsza uchyla normę wcześniejszą(pod
warunkiem, że nie jest normą niższego rzędu)

3. Reg

uła porządku treściowego – norma szczególna uchyla normę ogólną (pod warunkiem, że nie jest

normą niższego rzędu), późniejsze wprowadzenie normy ogólnej nie oznacza uchylenia normy
szczególnej.

Wnioskowania prawnicze
Reguły inferencyjne – są to logiczne lub quasi-logiczne reguły wnioskowań akceptowane szeroko i
wykorzystywane w odniesieniu do prawa stanowionego.
Rozumowanie inferencyjne

– Najpierw z przepisów prawnych zostaje z przepisów prawnych zostaje w

procesie wykładni wyinterpretowana norma N

1

a następnie przez zastosowanie reguł inferencyjnych normy

N

2

, N

3

, N

…

Przez Prawidłowo przeprowadzone rozumowania inferencyjnego powoduje, że

wyinterpretowanie normy N

2

, N

3

, N

…

uzyskują taką samą moc obowiązywania jak norma N

1

.

Najbardziej znane wnioskowania prawnicze:
1. Instrumentalne wynikanie norm z norm(wnioskowanie z celu na środki) – Chcąc zrealizować normę

będącą naszym celem, musimy zrealizować szereg innych norm będących środkami prowadzącymi do
celu. Inaczej mówiąc nakazane są wszystkie niezbędne do osiągnięcia celu, a zakazane te, które
uniemożliwiają osiągnięcie celu.

2. Argumentum a simili

I.

Analogia z ustawy(Analogia legis)

– polega na zastosowani do nieuregulowanego stanu

rzeczy, regulacji dotyczącej podobnego stanu rzeczy uregulowanego
(M a P n S a [podobne

do M] →S a P)

II.

Analogia z prawa(analogia iuris)

– polega na sformułowaniu nowej normy, która

regulowałaby stan rzeczy objęty luką w procesie stanowienia prawa.

3. Argumentum a contario – czyli wnioskowanie z przeciwieństwa(dotyczy sytuacji)

a. (p → q) → (~p → ~q) = „jeżeli p to q, a więc jeżeli nieprawda, że p to nieprawda że q”

b. (p ← q) →(~p → ~q) = „Tylko wtedy gdy p to q, a więc jeżeli nieprawda, że p to nieprawda że q”

c. (p ≡ q) → (~p → ~q) = „p zawsze i tylko wtedy, gdy q, a więc jeżeli nieprawda, że p to nieprawda że

q”

4. Argumentum a fortiori

a. A maiori ad minus. – Jeśli komuś nakazano\ dozwolono robić coś więcej to tym bardziej

nakazano\

dozwolono robić coś mniej.

b. Argumentum a minori ad maius. – Jeżeli komuś zakazano czynić coś mniej totem bardziej

zakazano robi

ć mu coś więcej.