6. OBLICZENIA TRAKCYJNE

Przejazd teoretyczny

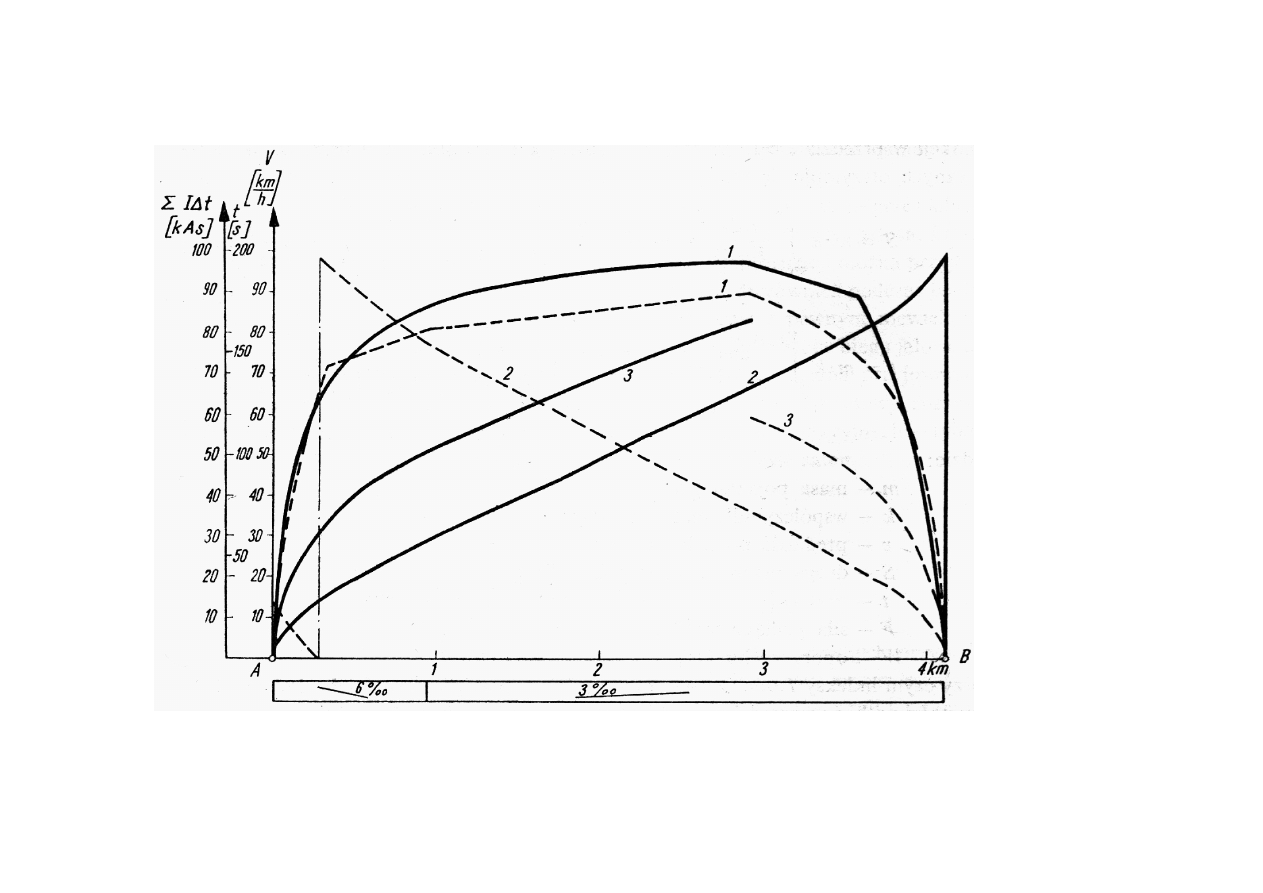
Teoretyczny wykres jazdy zespołu trakcyjnego na odcinku 4,1 km o profilu 6 i 3

0

/

00

1 – v = f(s), 2 – t = f(s), 3 - ∑I∆t = f(s)
linie ciągłe – jazda od A do B, linie przerywane – jazda od B do A

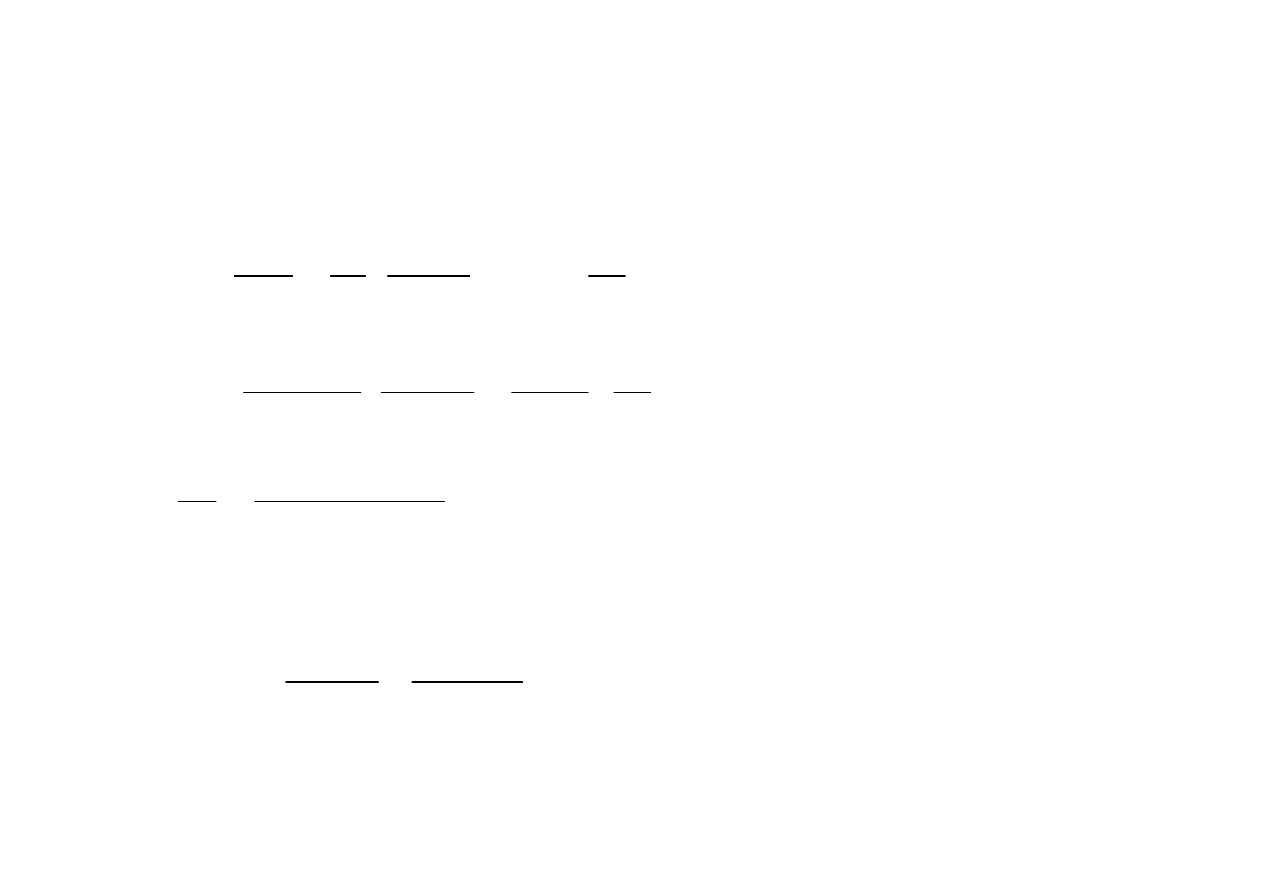
Metody analityczne wykonywania przejazdu opierają się na zasadniczych
równaniach ruchu pociągu.

k

p

dE

ds

F

=

⋅

ds

dv

v

m

v

m

ds

d

ds

dE

F

k

p

α

α

=













=

=

2

2

ds

dv

v

G

ds

vdv

g

G

F

p

127

,

0

6

,

3

1000

2

α

α

=

⋅

=

(

)

v

G

W

F

ds

dv

α

−

=

127

,

0

Rozwiązaniem tego równania jest:

∫

−

=

2

1

127

,

0

v

v

W

F

vdv

G

s

α

Zależność na dv/ds można zapisać w innej postaci, uwzględniającej czas t[sek]:

(

)

α

G

W

F

v

ds

dv

−

=

127

,

0

(

)

α

G

W

F

dt

ds

ds

dv

−

=

⋅

⋅

127

,

0

6

,

3

α

G

W

F

dt

dv

3

,

28

−

=

Rozwiązaniem tego równania jest:

∫

−

=

2

1

3

,

28

v

v

W

F

dv

G

t

α

Trudność w rozwiązaniu obu całek polega na tym, że zależności parametrów
F,W,v

podane są w postaci charakterystyk, które trudno wyrazić analitycznie.

Można je jednak obliczyć metodami przybliżonymi, zastępując różniczki
przyrostami skończonymi, a całki – sumami. Zakłada się, że wartość siły
przyspieszającej (F-W) jest w całym zakresie przedziału od v do v+∆v stała i
równa sile odpowiadającej prędkości v+∆v/2.

v

W

F

v

v

G

s

v

v

sr

sr

∆

⋅

−

∆

+

=

∑

2

1

2

127

,

0

α

∑

−

∆

=

2

1

3

,

28

v

v

sr

sr

W

F

v

G

t

α

Tok postępowania przy obliczaniu przejazdu teoretycznego wygląda pokrótce
następująco.
Dla założonej prędkości średniej w przedziale vśr=vp+∆v/2 ( gdzie vp jest
prędkością początkową w przedziale) wyznacza się kolejno:

- siłę pociągową F – z charakterystyki trakcyjnej,
- całkowite opory ruchu W – z odpowiedniej zależności,
- siłę przyspieszającą F-W,
- przyspieszenie średnie a,
- czas ∆t odpowiadający przyrostowi prędkości ∆v,
- sumę przyrostów czasu od chwili ruszenia ∑∆t,
- drogę ∆s odpowiadającą przyrostowi prędkości ∆v,
- drogę od chwili ruszenia ∑∆s,
- prąd jednego silnika I,
- iloczyn czasu i prądu pobieranego przez lokomotywę nI∆t, gdzie n jest

współczynnikiem uwzględniającym liczbę silników i ich połączenie,

- sumę przyrostów nI∆t,
- iloczyn I

2

∆t,

- sumę przyrostów I

2

∆t.

Na podstawie przeprowadzonych obliczeń uzyskuje się zależności

v=f(s)

oraz t=f(s).

Sumowanie iloczynów nI∆t służy do obliczenia całkowitego zużycia energii, zaś
sumowanie iloczynów I

2

∆t

do wyznaczenia prądu zastępczego.

t

t

I

I

t

z

∑

∆

=

0

2

∫

=

t

z

dt

I

t

I

0

2

1

gdzie t jest czasem całego cyklu pracy silnika

Całkowite zużycie energii trakcyjnej oblicza się na podstawie przejazdu
teoretycznego z zależności:

∑

∆

⋅

⋅

⋅

=

t

I

U

m

A

6

10

6

,

3

[kWh], I[A], ∆t[sek]

gdzie: U – napięcie przypadające na jeden silnik,

m=m

r

m

s

m

r

– liczba silników połączonych równolegle,

m

s

–

liczba silników połączonych szeregowo.

Napięcie U zależy od układu połączeń silników. Jeżeli do wzoru na
energię wprowadzić stałe napięcie sieci U

s

,

uzyska się:

10

6

,

3

10

6

,

3

10

6

,

3

6

6

6

∑

∑

∑

∆

⋅

⋅

⋅

=

∆

⋅

⋅

⋅

=

∆

⋅

⋅

⋅

=

t

I

m

U

t

I

U

m

t

I

m

U

m

A

r

s

s

r

s

s

Jednostkowe zużycie energii trakcyjnej

Bilans energii według jej ostatecznego przeznaczenia (dotyczy trakcji prądu

stałego z silnikami prądu stałego i rozruchem oporowym):

1.

praca użyteczna silników idąca na pokonanie oporów:
a) zasadniczych
b) krzywizn
c) wzniesień,

2.

straty przy przyhamowywaniu na większych spadkach,

3.

straty w oporach rozruchowych,

4.

straty dodatkowe w silnikach spowodowane ich pracą przy obniżonym
napięciu (połączenie szeregowe),

5.

straty przy hamowaniu na stacjach,

6.

straty normalne silników w połączeniu zasadniczym.

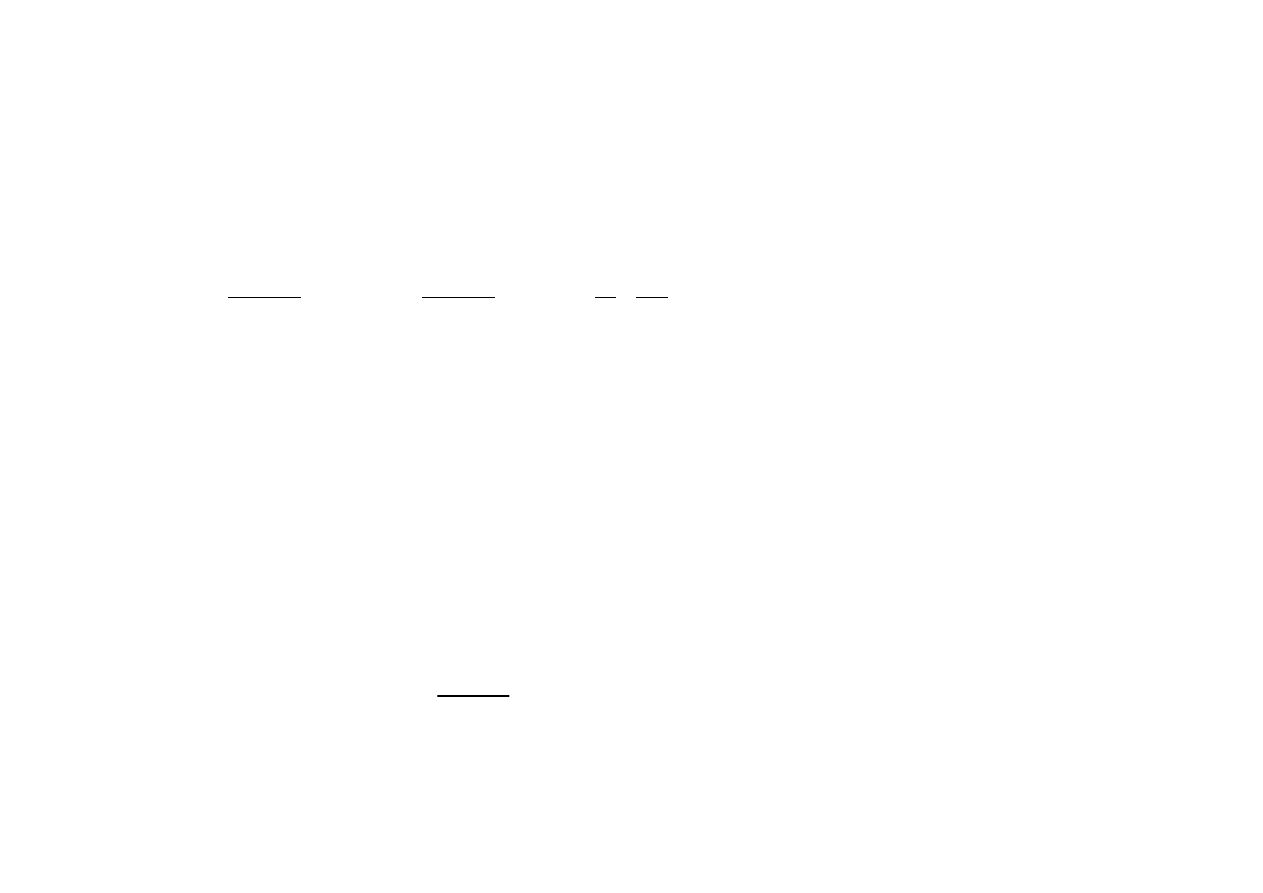
Jednostkowe zużycie energii na pokonanie zasadniczych oporów ruchu wynosi:

w

j

⋅

=

725

,

2

1

[Wh/tkm]

ds

v

k

w

s

ds

w

s

j

s

s

∫

∫



























+

=

⋅

=

0

2

0

0

1

10

1

725

,

2

725

,

2

Do rozwiązania całki potrzebna jest znajomość przebiegu v=f(s). Dla
uproszczenia przyjmuje się, że istnieje pewna prędkość zastępcza, z którą
pociąg przebywa większą część drogi, której kwadrat jest proporcjonalny do
iloczynu prędkości technicznej v

t

i prędkości maksymalnej v

m

. W ten sposób

jednostkowe zużycie energii na pokonanie zasadniczych oporów ruchu wyraża
się wzorem:













+

⋅

=

k

v

v

w

j

m

t

100

725

,

2

0

1

[Wh/tkm]

Łuki na trasie powodują wzrost jednostkowego zużycia energii o składnik:

ksr

w

j

⋅

=

725

,

2

2

[Wh/tkm]

gdzie w

ksr

– średnie jednostkowe opory krzywizn dla całej trasy.

Jednostkowe zużycie energii na pokonanie wzniesień to:

0

3

725

,

2

725

,

2

i

s

h

j

⋅

±

=

±

=

[Wh/tkm]

gdzie: h [m]– różnica poziomów miedzy stacją końcową a początkową,

s [km] – odległość między stacją początkową i końcową.

Na linii o długości s średnie dodatkowe opory wywołane przyhamowywaniem
wynoszą:

(

)

i

i

w

sp

s

w

i

s

i

∆

⋅

−

=

∑

〉

1

gdzie: i

>w

– spadek przekraczający opory ruchu przy prędkości

dopuszczalnej,

w

i

– opory ruchu pociągu przy prędkości dopuszczalnej,

∆s

i

– droga przyhamowywania.

Jednostkowe zużycie energii na pokrycie przyhamowań na spadkach wynosi:

sp

i

j

⋅

=

725

,

2

4

[Wh/tkm]

Jednostkowa energia kinetyczna pociągu o prędkości początku hamowania
v

H

[km/h]

liczona na kołach pociągu jest proporcjonalna do wielkości:

2

'

10

54

,

2













=

H

v

h

α

[m]

zaś praca użyteczna na drodze hamowania, idąca na pokonanie oporów ruchu,
obliczona na jednostkę masy pociągu, jest proporcjonalna do wielkości:

2

''

10

54

,

2













⋅

⋅

=

H

H

Hsr

v

f

w

h

α

gdzie: f

H

– jednostkowa siła hamująca,

w

Hsr

– średnie jednostkowe opory ruchu na drodze hamowania.

Jeżeli

zatrzymanie

pociągu

odbywa

jednorazowo

na

odległości

międzyprzystankowej L[km], to jednostkowe zużycie energii trakcyjnej
(mierzone na kołach) traconej przy hamowaniu będzie wyrażać się
zależnością:

[m]

L

h

h

j

''

'

5

725

,

2

−

=

2

'

2

2

2

''

'

10

54

,

2

1

10

54

,

2

10

54

,

2

10

54

,

2













=













−













=













−













=

−

H

H

Hsr

H

H

H

Hsr

H

v

f

w

v

v

f

w

v

h

h

α

α

α

α













−

=

H

Hsr

f

w

1

'

α

α

2

0

10

2

1













+

=

H

Hsr

v

k

w

w

Zatem jednostkowe zużycie energii traconej przy hamowaniu będzie
wyrażać się zależnością:

2

'

5

10

54

,

2

725

,

2













=

H

v

L

j

α

Analizując moc i straty występujące podczas rozruchu pojazdu oraz czasy trwania
rozruchu przy poszczególnych połączeniach silników można dowieść, że stosunek
strat w oporach do energii pobranej z sieci w czasie rozruchu wynosi:

- dla pojazdu 4-silnikowego

- dla pojazdu 6-silnikowego

k

−

⋅

=

1

1

2

1

µ

k

k

−

+

⋅

=

1

1

3

1

µ

gdzie k oznacza stosunek strat w
miedzi silników w końcowej
fazie rozruchu do mocy
lokomotywy mierzonej na
zaciskach silników.

Jednostkowa energia kinetyczna pociągu o prędkości końca rozruchu v

R

[km/h]

liczona na kołach pociągu jest proporcjonalna do:

2

'

10

54

,

2













=

R

v

h

α

[m]

Praca użyteczna na drodze rozruchu, idąca na pokonanie oporów ruchu,
obliczona na jednostkę masy pociągu, jest proporcjonalna do wielkości:

2

''

10

54

,

2













⋅

=

R

R

Rsr

v

f

w

h

α

[m]

gdzie: f

R

– jednostkowa siła rozruchowa,

w

Rsr

– średnie jednostkowe opory ruchu na drodze rozruchu.

Jednostkowe zużycie energii, mierzone na kołach, na jeden rozruch przypadający
na odległości międzyprzystankowej L[km] wynosi:

L

h

h

j

R

''

'

725

,

2

+

⋅

=

2

''

2

2

''

'

10

54

,

2

10

54

,

2

10

54

,

2













=













⋅

+













=

+

R

R

R

Rsr

R

v

v

f

w

v

h

h

α

α

α

gdzie:













+

=

R

Rsr

f

w

1

''

α

α

2

0

10

2

1













+

=

R

Rsr

v

k

w

w

2

''

10

54

,

2

725

,

2













=

R

R

v

L

j

α

To zużycie energii zostało już uwzględnione w bilansie w innych składnikach:
jednostkowym zużyciu energii na pokonanie oporów ruchu na całej drodze L i
jednostkowym zużyciu energii traconym w hamulcach.

Straty w oporach rozruchowych wynoszą:

A

A

⋅

=

µ

'

gdzie A – energia pobrana z sieci.

Zatem jednostkowe zużycie energii na pokrycie strat w oporach rozruchowych,
liczone na kołach lokomotywy, określa zależność:

2

''

6

10

54

,

2

725

,

2













=

R

v

L

j

µα

przy założeniu, że sprawność silników przy rozruchu jest równa ogólnej
sprawności silników η.

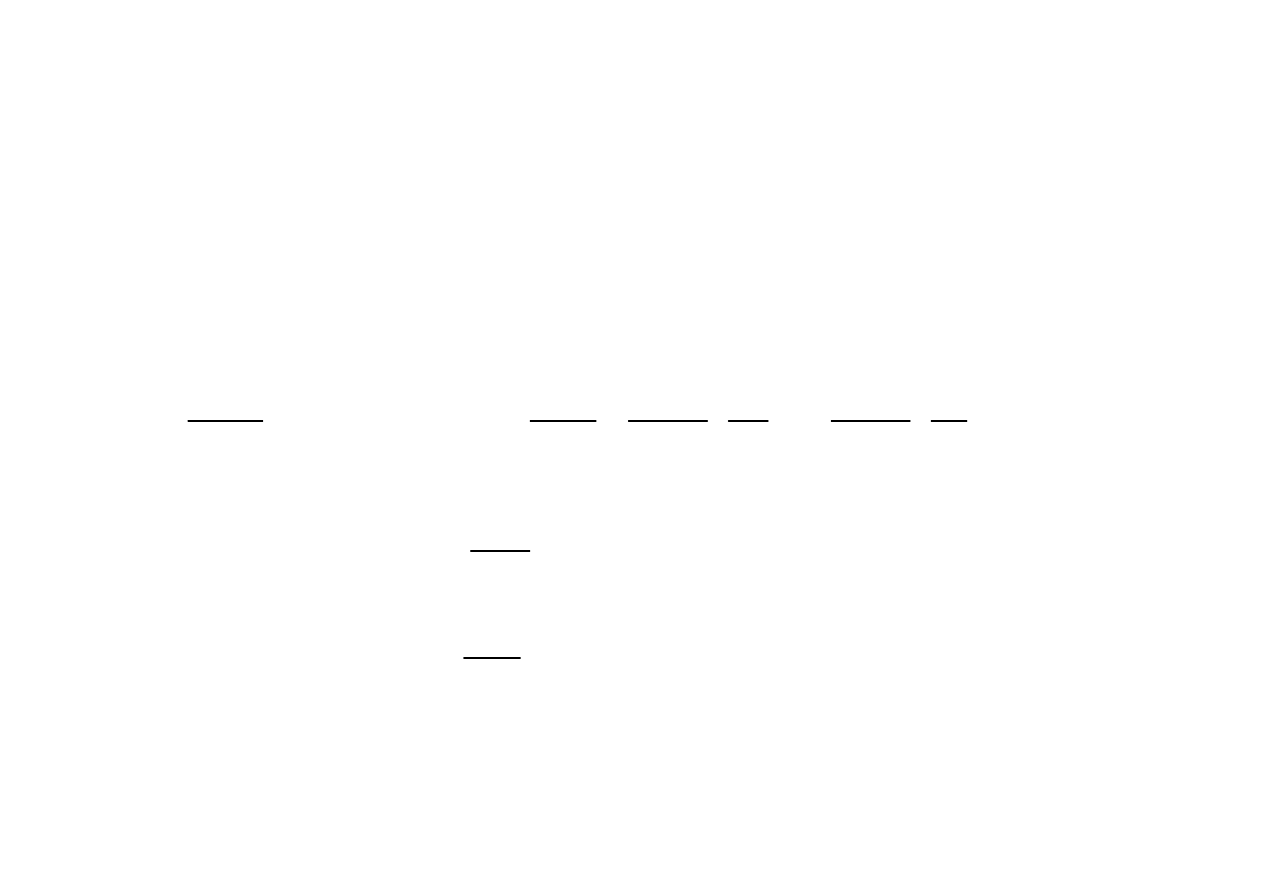
Całkowite jednostkowe zużycie energii mierzone na obwodzie kół napędnych
jest sumą wszystkich podanych składników

6

5

4

3

2

1

j

j

j

j

j

j

j

+

+

+

+

+

=

Całkowite jednostkowe zużycie energii mierzone na zaciskach silników
określa zależność:



























+













+

+

±

+

+

=

2

''

2

'

0

0

0

10

54

,

2

10

54

,

2

100

725

,

2

R

H

t

M

sp

k

z

v

L

v

L

k

v

v

i

i

w

w

j

µα

α

ηη

[Wh/tkm]

gdzie:













−

=

H

Hsr

f

w

1

'

α

α













+

=

R

Rsr

f

w

1

''

α

α

Dla ułatwienia obliczeń, przyjmuje się, że w przeciętnych warunkach:
µ

BB

≈ 0,55 oraz µ

CC

≈ 0,40.

Przykładowe wartości jednostkowego zużycia energii dla różnego rodzaju pociągów
są następujące:

rodz. poc. m[t]

L[km]

v

M

v

t

v

H

v

R

j

0

[Wh/tkm]

pospieszny 600 35 120 95

80 45 17,8

osobowy 450 6 100 70

70 45 24,4

towarowy 1800 45 70 55

45 45 10,2

zespół trakc. 160 3,5 90 65 70 35 33,5

Na podstawie danej prędkości handlowej pociągu V[km/h] i jego masy M[t] można,
znając jednostkowe zużycie energii, określić średnią moc czerpaną przez pociąg z
sieci:

1000

0

VM

j

N

sr

=

oraz średni prąd silników lokomotywy:

mU

VM

j

I

sr

0

=

gdzie: U [V] – napięcie na zaciskach silników,

m

– liczba silników.

[A]

[kW]