
W
E
OD
W czasie trwa
EGZA
D ROK
M
PO
PRZYK
ania egzami
AMIN
KU SZ
MAT
ZIOM
KŁADOW
inu zdający
linijki i
Czas
G
N MA
ZKOL
TEMA
M ROZ
WY ZES
y może korz
i cyrkla ora
s pracy: 1
GRUDZIEŃ
ATUR
NEGO
ATYK
SZERZ
STAW Z
ystać z zest
z kalkulator
180 minut
Ń 2013
RALN
O 2014
KA
ZONY
ZADAŃ
tawu wzoró
ra.
t
NY
4/2015
Y
(A1)
w matematy
5
ycznych,
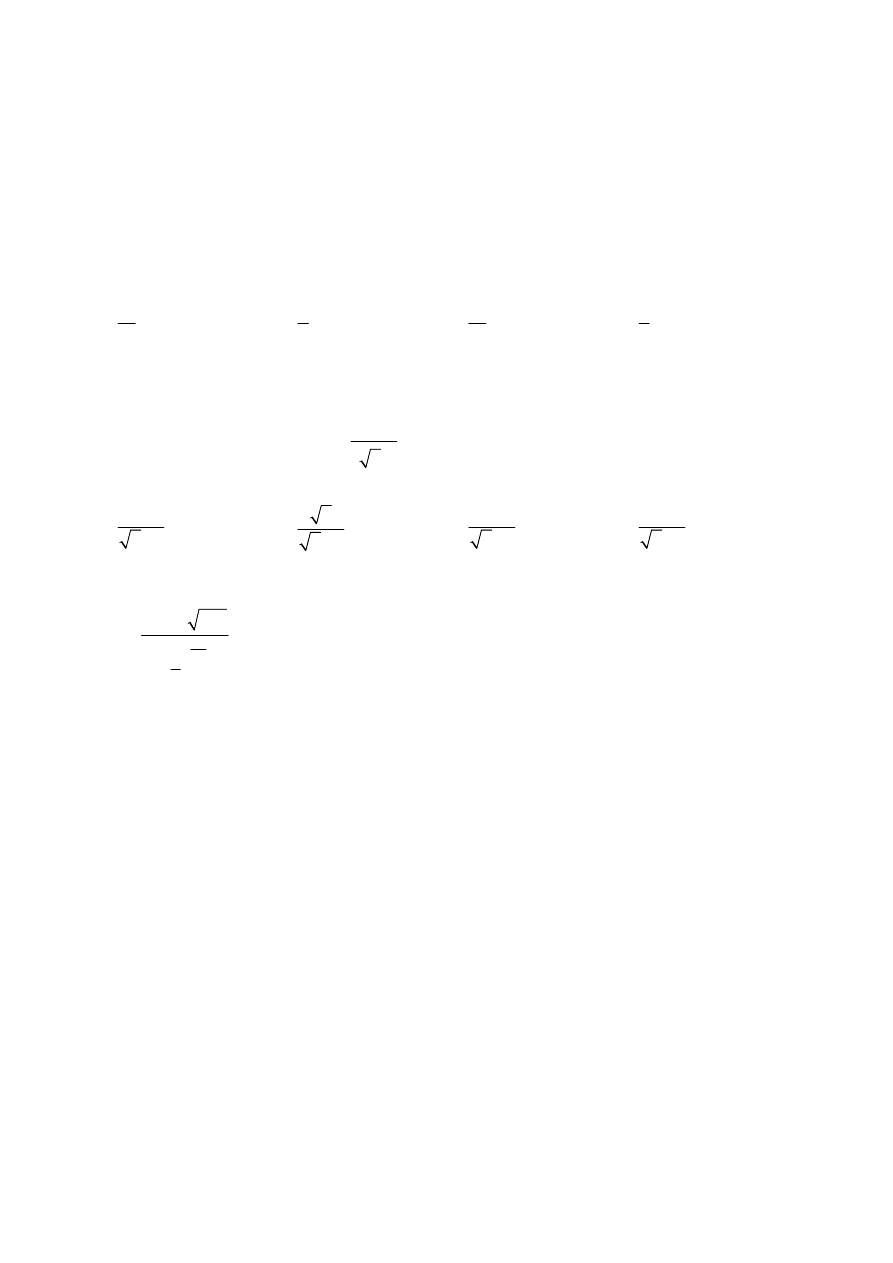
Strona 2 z 19
ZADANIA ZAMKNIĘTE
W zadaniach 1–5 wybierz i zaznacz poprawną odpowiedź
Zadanie 1. (0–1)
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała
i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz
symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną
kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę
z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A.
1
15
B.
2
5
C.
7
15
D.
3
5
Zadanie 2. (0–1)
Dany jest nieskończony ciąg geometryczny
n
a określony wzorem
3
2
n
n
a
dla
1, 2,3,...
n
.
Suma wszystkich wyrazów tego ciągu jest równa
A.
1
2 1
B.
2
2 1
C.
2
2 1
D.
3
2 1
Zadanie 3. (0–1)
Liczba
3
665
92
152
3
27
3
1
3
jest równa
A.
725
3
B.
1995
3
C.
2015
3
D.
2045
3
Zadanie 4. (0–1)
Okrąg
1
o ma równanie
2
2
1
25
x
y
, a okrąg
2
o ma równanie
2
2
1
9
x
y
. Określ
wzajemne położenie tych okręgów.
A. Te okręgi przecinają się w dwóch punktach.
B. Te okręgi są styczne.
C. Te okręgi nie mają punktów wspólnych oraz okrąg
1
o leży w całości wewnątrz okręgu
2
o .
D. Te okręgi nie mają punktów wspólnych oraz okrąg
2
o leży w całości wewnątrz okręgu
1
o .
Zadanie 5. (0–1)
Dla każdego
suma sin
sin 3
jest równa
A. sin 4
.
B. 2sin 4
.
C. 2sin 2 cos
.
D. 2sin cos 2
.

Strona 3 z 19
BRUDNOPIS
Strona 4 z 19
ZADANIA OTWARTE
W zadaniach 6–9 zakoduj wynik w kratkach zamieszczonych obok polecenia. W zadaniach
10–18 rozwiązania należy zapisać w wyznaczonych miejscach pod treścią zadania.
Zadanie 6. (0–2)
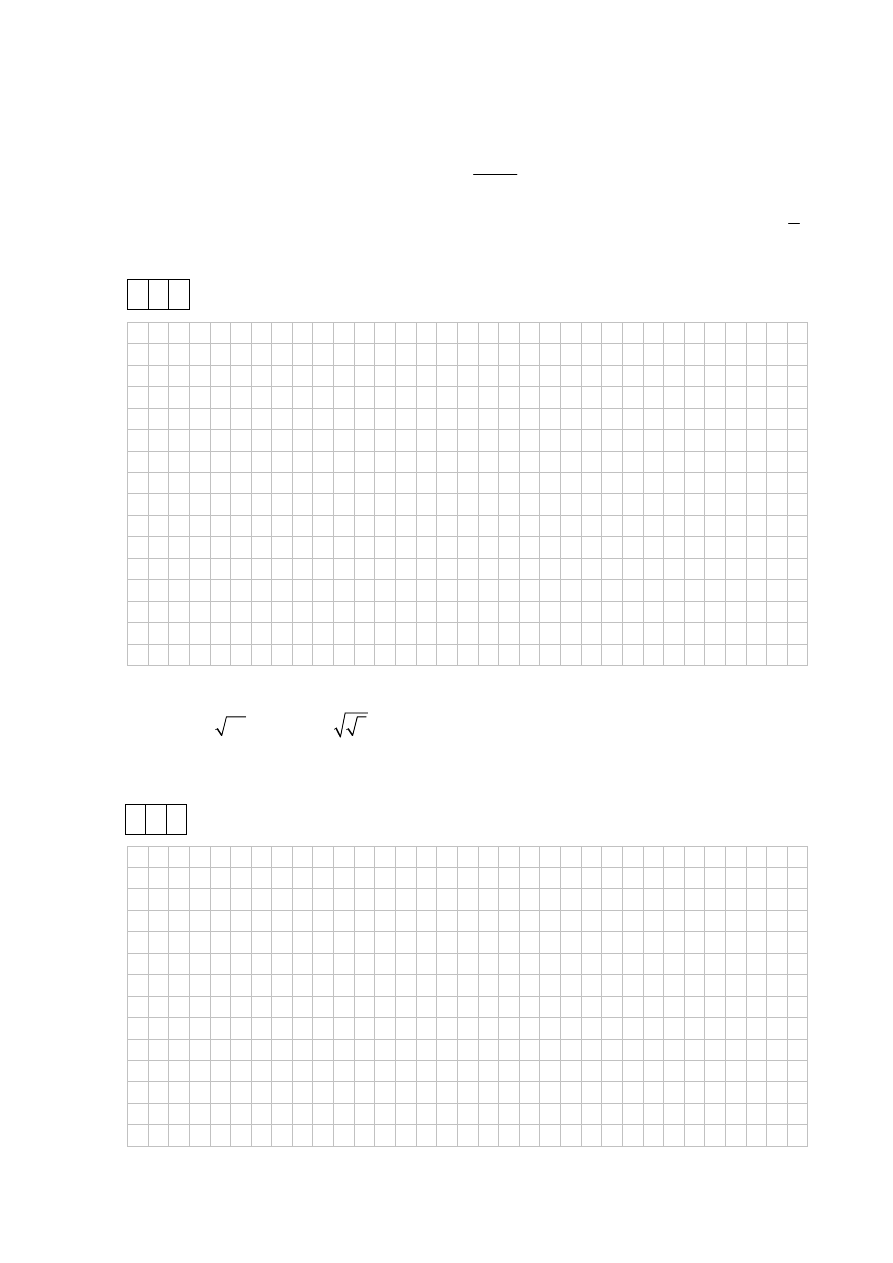
Liczba n jest najmniejszą liczbą całkowitą spełniającą równanie
2
57
39
x
x
.
Zakoduj cyfry: setek, dziesiątek i jedności liczby n .
Zadanie 7. (0–2)
Oblicz granicę ciągu
2
3
5
2
lim
8
7
4
n
n
n
n
n
.
Zakoduj trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego obliczonej granicy.
Strona 5 z 19
Zadanie 8. (0–2)
Dana jest funkcja f określona wzorem
2
8
6
x
f x
x
dla każdej liczby rzeczywistej x. Oblicz wartość pochodnej tej funkcji w punkcie
1
2
x
.
Zakoduj trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.
Zadanie 9. (0–2)
Oblicz
3 3
4
3
3
3
log
27 log log
3
.
Zakoduj cyfrę jedności i dwie pierwsze cyfry po przecinku rozwinięcia dziesiętnego
otrzymanego wyniku.
Strona 6 z 19
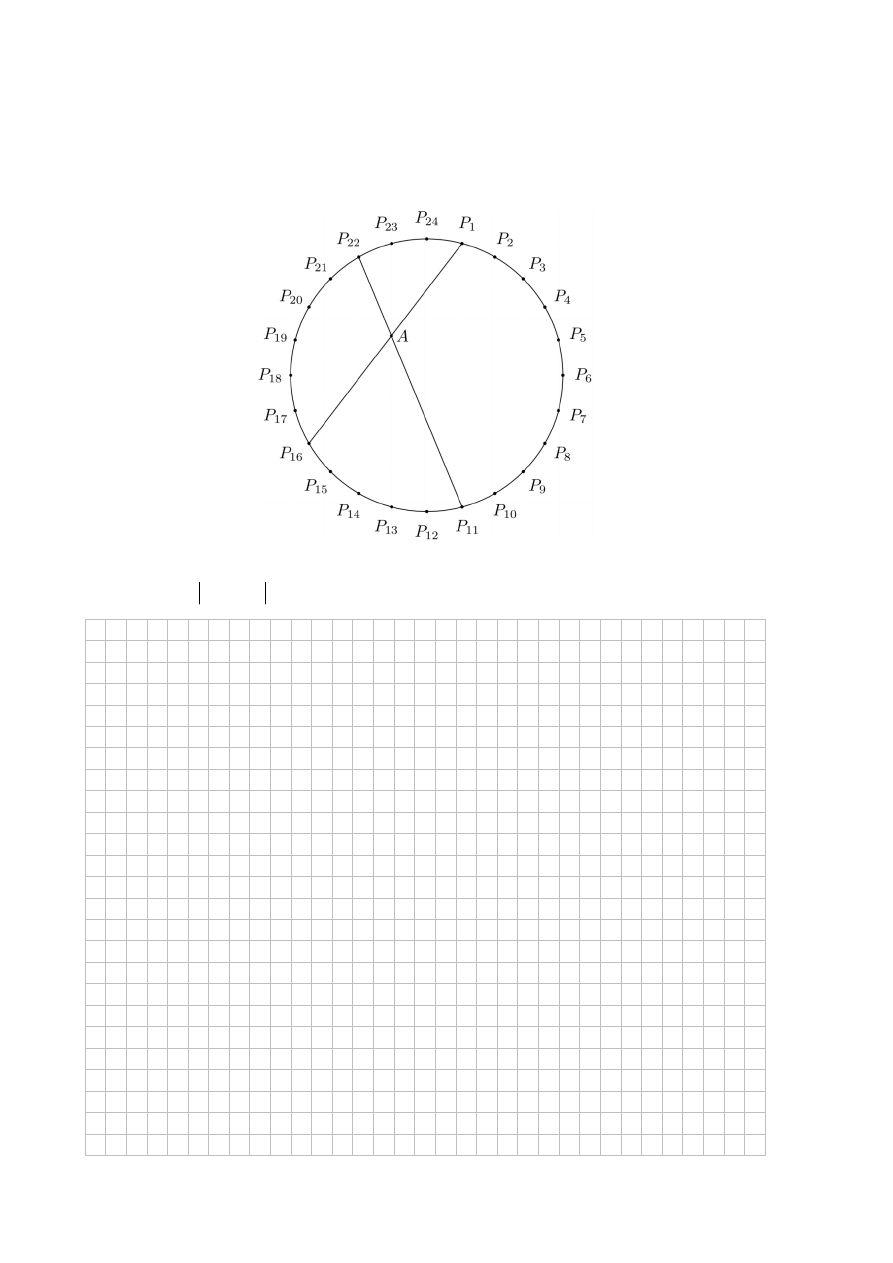
Zadanie 10. (0–3)
Punkty
1
2
3
23
24
, , , ,
,
P P P
P P
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt A jest
punktem przecięcia cięciw
11 22
P P i
1 16
PP .
Udowodnij, że
16
11
60
P AP
.

Strona 7 z 19

Strona 8 z 19
Zadanie 11. (0–3)
Udowodnij, że dla każdej liczby rzeczywistej x i każdej liczby rzeczywistej m prawdziwa jest
nierówność
2
2
20
24
18
4
12
5
x
mx
m
x
m
.

Strona 9 z 19
Zadanie 12. (0–3)
Janek przeprowadza doświadczenie losowe, w którym jako wynik może otrzymać jedną
z liczb: 0,1, 2, 3, 4, 5, 6. Prawdopodobieństwo
k
p otrzymania liczby k jest dane wzorem:
6
1
64
k
p
k
.
Rozważamy dwa zdarzenia:
zdarzenie
A
polegające na otrzymaniu liczby ze zbioru
1, 3, 5
,
zdarzenie
B
polegające na otrzymaniu liczby ze zbioru
2, 3, 4, 5, 6
.
Oblicz prawdopodobieństwo warunkowe
P A B
.
Odpowiedź:
.......................................................................................................................................................

Strona 10 z 19
Zadanie 13. (0–3)
Wyznacz wszystkie wartości parametru m, dla których prosta o równaniu
2
3
y mx
m
ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie
0,0
S
i promieniu
3
r
.
Odpowiedź:
........................................................................................................................................................

Strona 11 z 19
Zadanie 14. (0–3)
Dana jest parabola o równaniu
2
1
y x
i leżący na niej punkt
A
o współrzędnej x równej 3.
Wyznacz równanie stycznej do tej paraboli w punkcie
A
.
Odpowiedź:
………………………………………………………………………………………………………
Strona 12 z 19
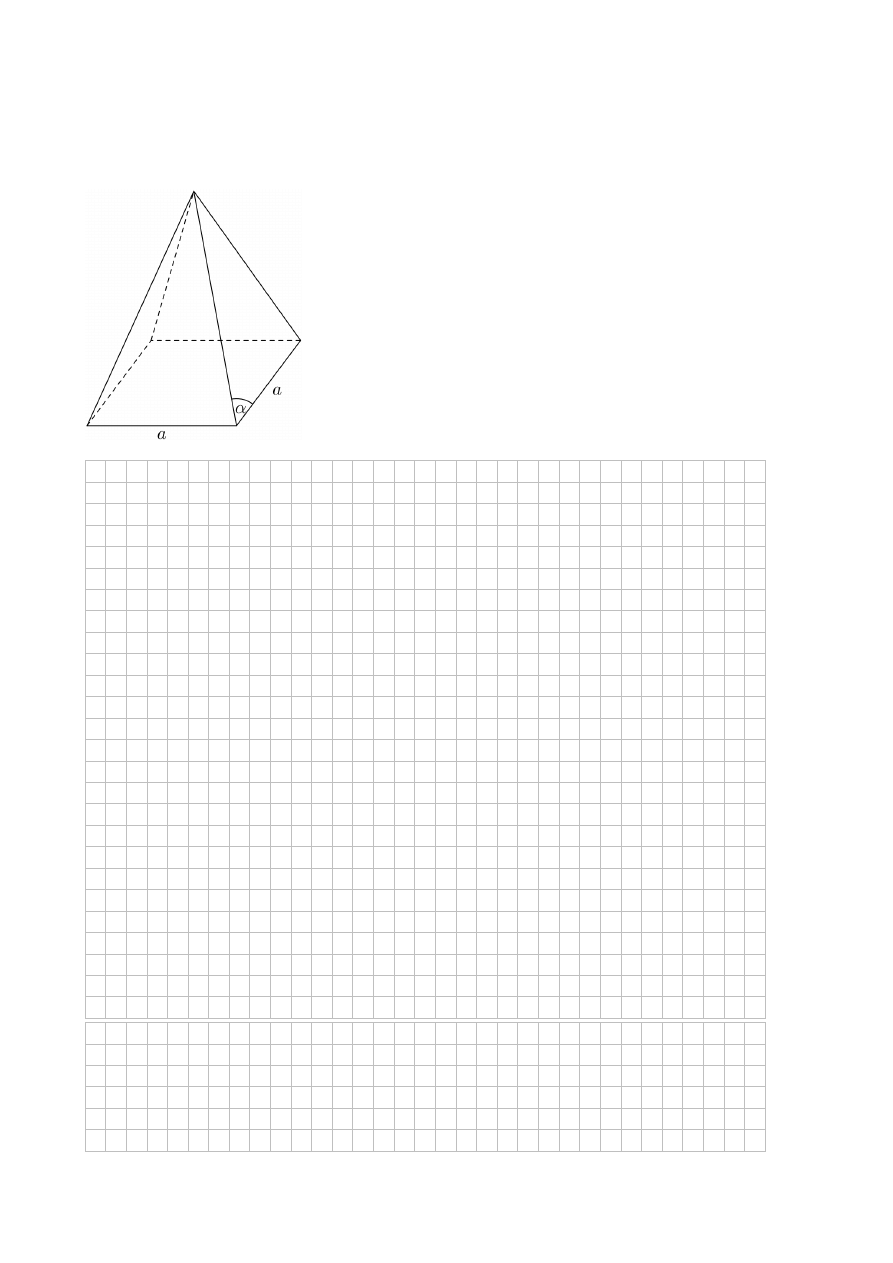
Zadanie 15. (0–3)
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między
krawędzią boczną, a krawędzią podstawy ma miarę
45
(zobacz rysunek). Oblicz objętość
tego ostrosłupa.

Strona 13 z 19
Odpowiedź:
…………………………………………………………………………………………………….. .
Strona 14 z 19
Zadanie 16. (0–6)
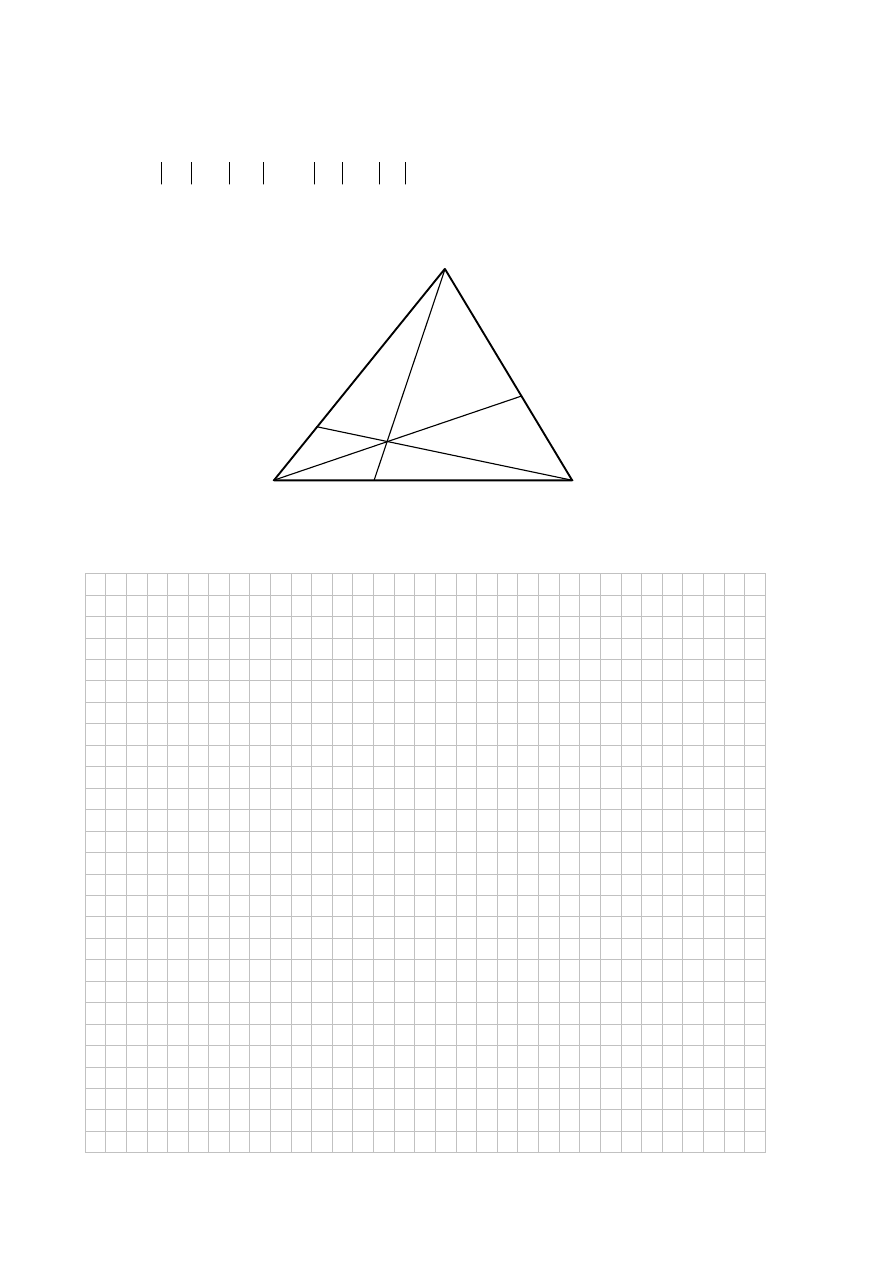
Punkty M i L leżą odpowiednio na bokach AB i AC trójkąta ABC, przy czym zachodzą
równości
2
MB
AM
oraz
3
LC
AL
. Punkt S jest punktem przecięcia odcinków BL
i CM. Punkt K jest punktem przecięcia półprostej AS z odcinkiem BC (zobacz rysunek).
Pole trójkąta ABC jest równe 660. Oblicz pola trójkątów: AMS, ALS, BMS i CLS.
A
B
C
M
L
K
S

Strona 15 z 19
Odpowiedź:
......................................................................................................................................................
Strona 16 z 19
Zadanie 17. (0–6)
Oblicz, ile jest stucyfrowych liczb naturalnych o sumie cyfr równej 4.
Odpowiedź:
........................................................................................................................................................
Strona 17 z 19
Zadanie 18. (0–7)
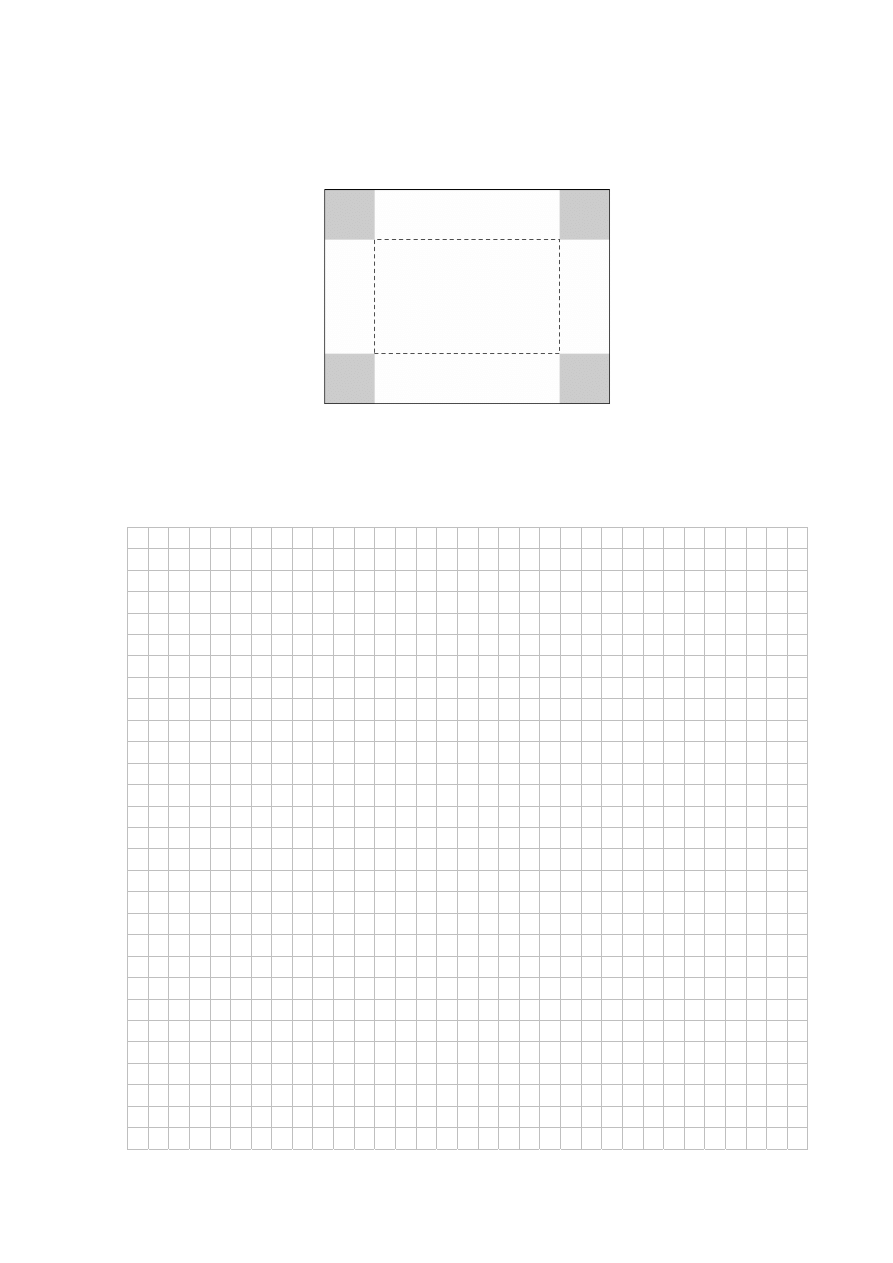
Dany jest prostokątny arkusz kartonu o długości 80 cm i szerokości 50 cm. W czterech rogach
tego arkusza wycięto kwadratowe naroża (zobacz rysunek).
Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób
prostopadłościenne pudełko (bez przykrywki). Oblicz długość boku każdego z wyciętych
kwadratowych naroży, dla której objętość otrzymanego pudełka jest największa. Oblicz tę
maksymalną objętość.

Strona 18 z 19
Odpowiedź:
........................................................................................................................................................

Strona 19 z 19
BRUDNOPIS
Wyszukiwarka
Podobne podstrony:
mat 2015 podstawowa przykładowy arkusz nowa odp
mat 2015 probna nowa
mat 2015 nowa
Zadania z przykładowego arkusza matura 2015 rozwiązania
Odpowiedzi Przykladowy arkusz PP Fizyka (2)
Mat na inf arkusz kalk, Powtórka arkusze kalkulacyjne
Odpowiedzi Przykladowy arkusz PR Polski
Odpowiedzi Przykladowy arkusz PP Biologia
1 5 Przykladowy arkusz 2 Matematy (2)
odpowiedzi przykladowy arkusz maturalny poziom rozszerzony wyd 2013 r
Odpowiedzi Przykladowy arkusz 2 ZR Polski
Odpowiedzi Przykladowy arkusz PR Historia Op 11
Odpowiedzi Przykladowy arkusz PR Polski
Odpowiedzi Przykladowy arkusz PP Polski
więcej podobnych podstron