Optyczna spektroskopia oscylacyjna

w badaniach powierzchni

Zalety oscylacyjnej spektroskopii optycznej

u

ż

ycie fotonów jako cz

ą

steczek wzbudzaj

ą

cych i rejestrowanych nie

wymaga u

ż

ycia pró

ż

ni (mo

ż

liwo

ść

prowadzenia pomiarów in situ)

znacznie mniejsze ryzyko modyfikacji próbki ni

ż

przy u

ż

yciu

elektronów

du

ż

o wi

ę

ksza rozdzielczo

ść

(kilka cm

-1

w RAIRS; 20-30 cm

-1

w HEELS)

wi

ę

kszy zasób informacji o próbce („widzimy” nie tylko atomy, ale te

ż

wi

ą

zania mi

ę

dzy nimi).

Ale:

Mniejsza czuło

ść

ni

ż

w spektroskopii elektronów

⇒

⇒

⇒

⇒

konieczno

ść

zapewnienia odpowiednio wysokiego st

ęż

enia

badanych cz

ą

steczek na powierzchni

Podstawy fizyczne spektroskopii oscylacyjnej

Ka

ż

da cz

ą

steczka w T > 0 K wykonuje drgania.

Liczba ró

ż

nych drga

ń

wynosi: 3N-5 - dla cz

ą

steczek liniowych,

3N-6 - dla cz

ą

steczek nieliniowych

Energia tych drga

ń

jest kwantowana; dozwolone warto

ś

ci energii oscylacji

w przybli

ż

eniu oscylatora harmonicznego wynosz

ą

:

Aby wzbudzi

ć

okre

ś

lone drganie potrzebna jest energia:

(

)

(

)

osc

osc

osc

h

h

h

E

E

E

ν

ν

ν

υ

υ

=

+

−

+

=

−

=

+

2

1

2

1

1

0

1

-

oscylacyjna liczba kwantowa

( = 0,1,2...)

-

cz

ę

sto

ść

drgania

(

)

2

1

+

=

υ

ν

osc

osc

h

E

υ

osc

ν

υ

Aby drganie mogło zosta

ć

wzbudzone poprzez absorpcj

ę

fotonu, musz

ą

by

ć

spełnione nast

ę

puj

ą

ce warunki (tzw. reguły wyboru)

1. w trakcie drgania musi zmienia

ć

si

ę

moment dipolowy cz

ą

steczki :

2. energia fotonu musi by

ć

równa ró

ż

nicy energii s

ą

siaduj

ą

cych poziomów

oscylacyjnych, czyli:

(tylko w odniesieniu do oscylatora harmonicznego)

Cz

ę

sto

ść

drgania w przybli

ż

eniu harmonicznym wynosi:

red

osc

m

f

π

ν

2

1

=

f - stała siłowa drgania, charakteryzuje „moc” wi

ą

zania

m

red

- masa zredukowana atomów tworz

ą

cych oscylator

⇒

cz

ę

sto

ść

drgania jest cech

ą

charakterystyczn

ą

cz

ą

steczki

0

≠













∂

∂

Q

µ

osc

h

E

E

h

ν

ν

υ

υ

=

−

=

+

1

C

O

C

O

C H

3

C

H

3

C

O

CH

3

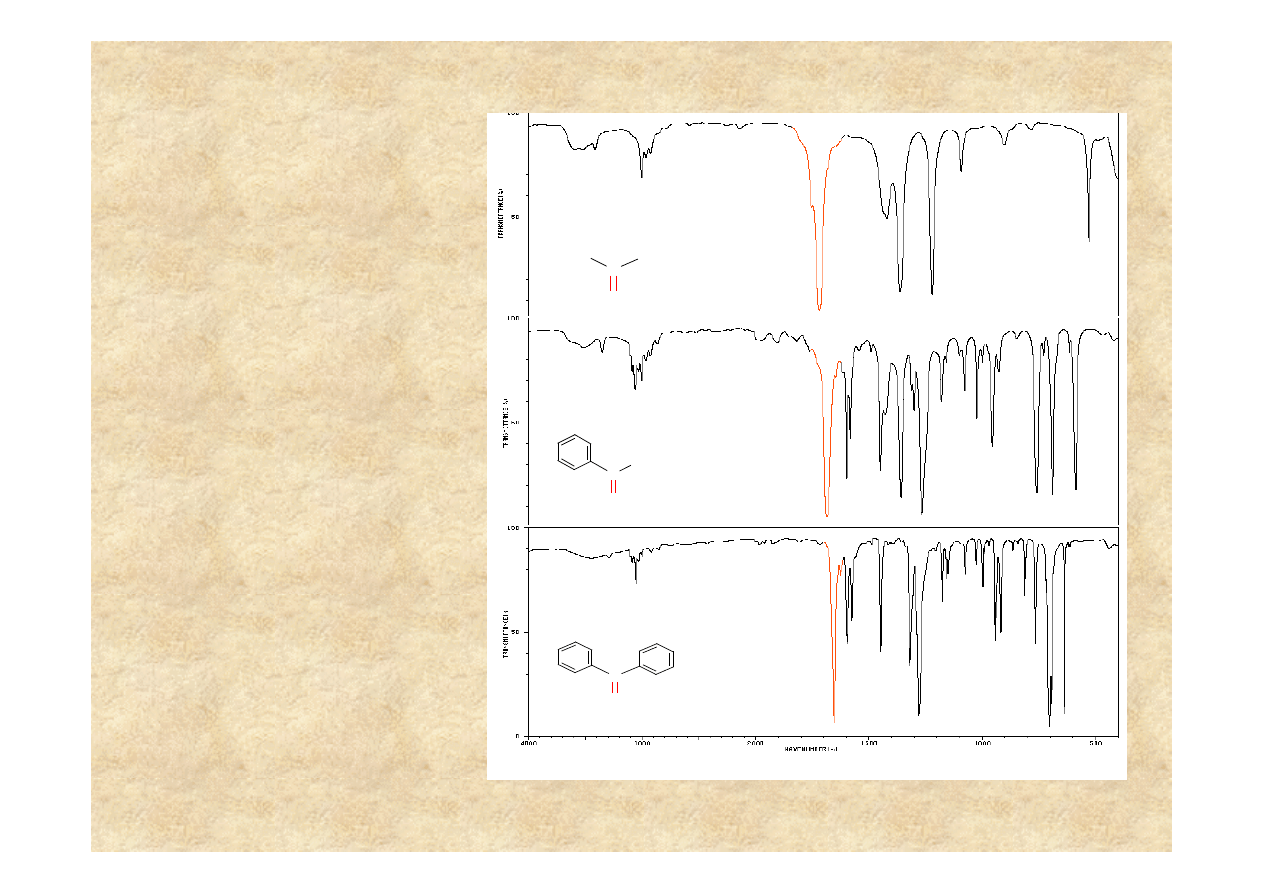
Drganie normalne anga

ż

uje

wszystkie (lub wi

ę

kszo

ść

)

atomów cz

ą

steczki.

Niektóre drgania odbywaj

ą

si

ę

z udziałem tylko kilku

najbli

ż

ej zwi

ą

zanych ze sob

ą

atomów (grup funkcyjnych).

Cz

ę

sto

ś

ci tych drga

ń

(tzw. cz

ę

sto

ś

ci

charakterystyczne),

słabo zale

żą

od rodzaju

cz

ą

steczki i stanowi

ą

podstaw

ę

identyfikacji

okre

ś

lonej grupy funkcyjnej.

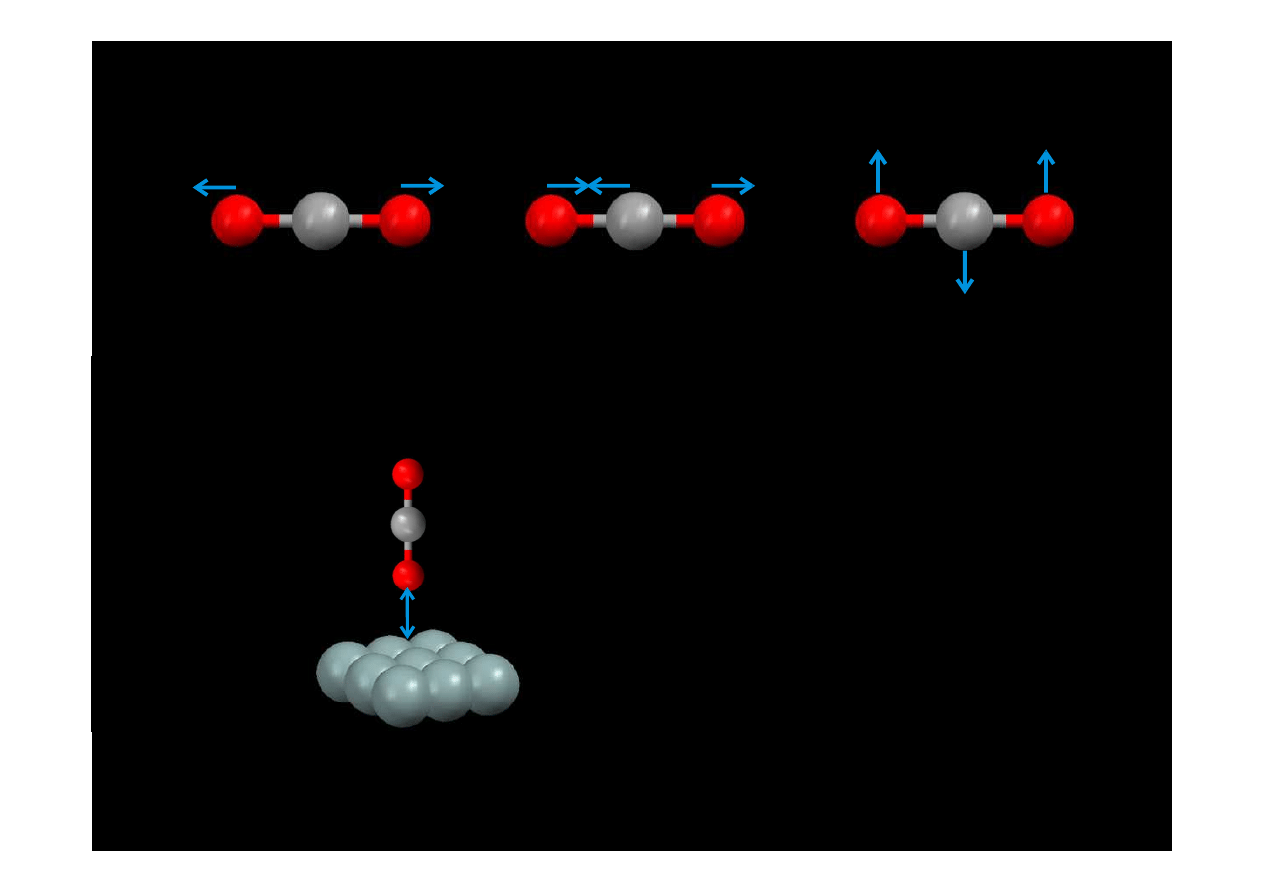
Drgania normalne swobodnej cz

ą

steczki CO

2

Siła wi

ą

za

ń

w cz

ą

steczce

zaadsorbowanej na powierzchni

ulega

zmianie

⇒

obserwujemy zmian

ę

cz

ę

sto

ś

ci drga

ń

normalnych (głównie rozci

ą

gaj

ą

cych).

Tworz

ą

si

ę

nowe (słabe) wi

ą

zania

⇒

w widmie pojawiaj

ą

si

ę

nowe pasma

przy niskich cz

ę

sto

ś

ciach.

i

dodatkowe drganie cz

ą

steczki zaadsorbowanej na powierzchni

(drganie nieaktywne
w podczerwienie)

Spektroskopia transmisyjna nie jest metod

ą

powierzchniowo specyficzn

ą

.

Mo

ż

na j

ą

wykorzysta

ć

do badania cienkich filmów zaadsorbowanych na

powierzchni (wykonujemy widmo samego no

ś

nika oraz no

ś

nika z filmem;

odejmuj

ą

c widma od siebie uzyskujemy widmo samego filmu).

I ( )

0

ν

I( )

ν

d

Nat

ęż

enie monochromatycznej wi

ą

zki

ś

wiatła zmniejsza si

ę

po przej

ś

ciu przez

próbk

ę

w wyniku absorpcji

( )

( ) (

)

d

k

I

I

−

=

exp

0

ν

ν

( )

( )

( )

d

c

I

I

A

ε

ν

ν

ν

=

=

0

log

Wielko

ś

ci

ą

charakteryzuj

ą

c

ą

intensywno

ść

absorpcji jest absorbancja, A(

ν

)

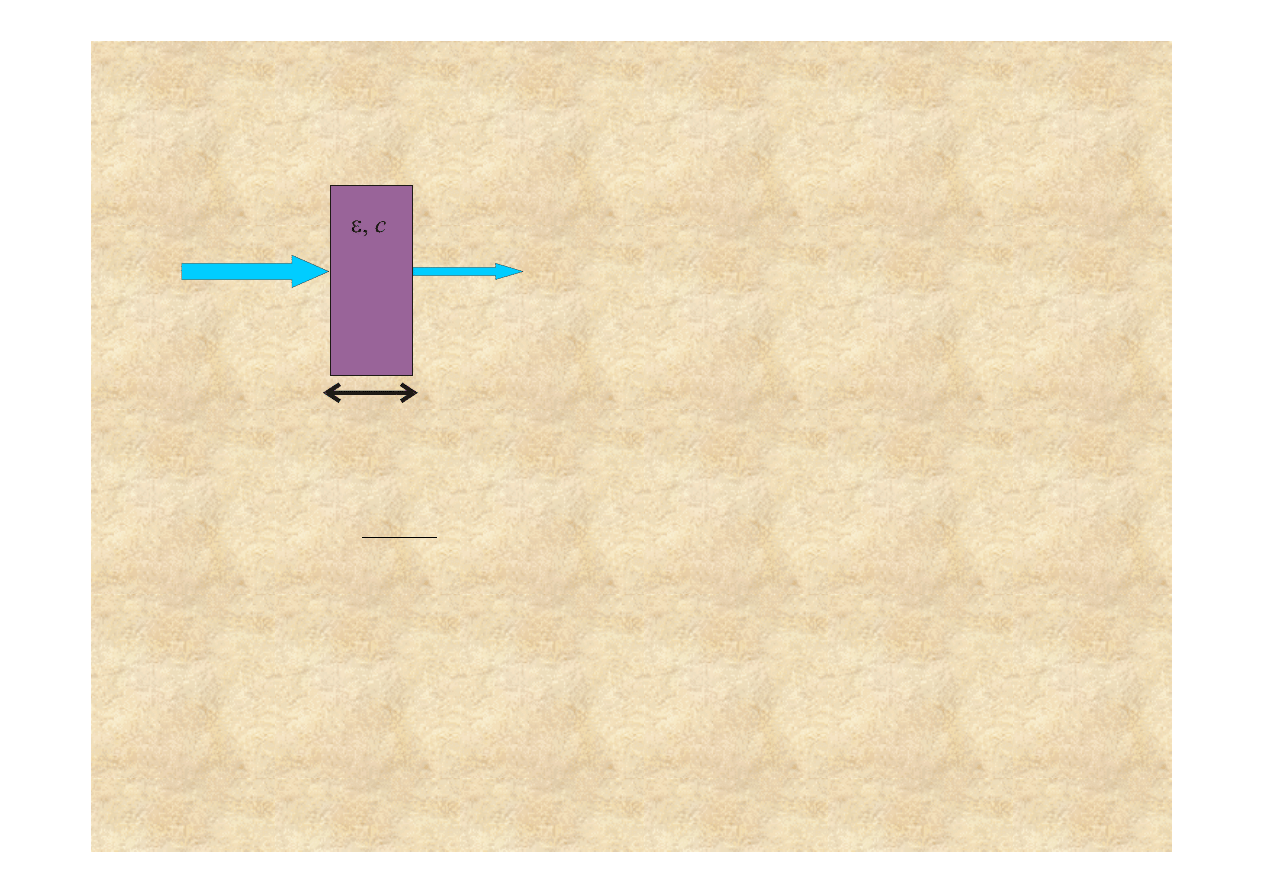
Spektroskopia transmisyjna

(prawo Lamberta-Beera)

Widmo transmisyjne

- wykres zale

ż

no

ś

ci A = f(

ν

)

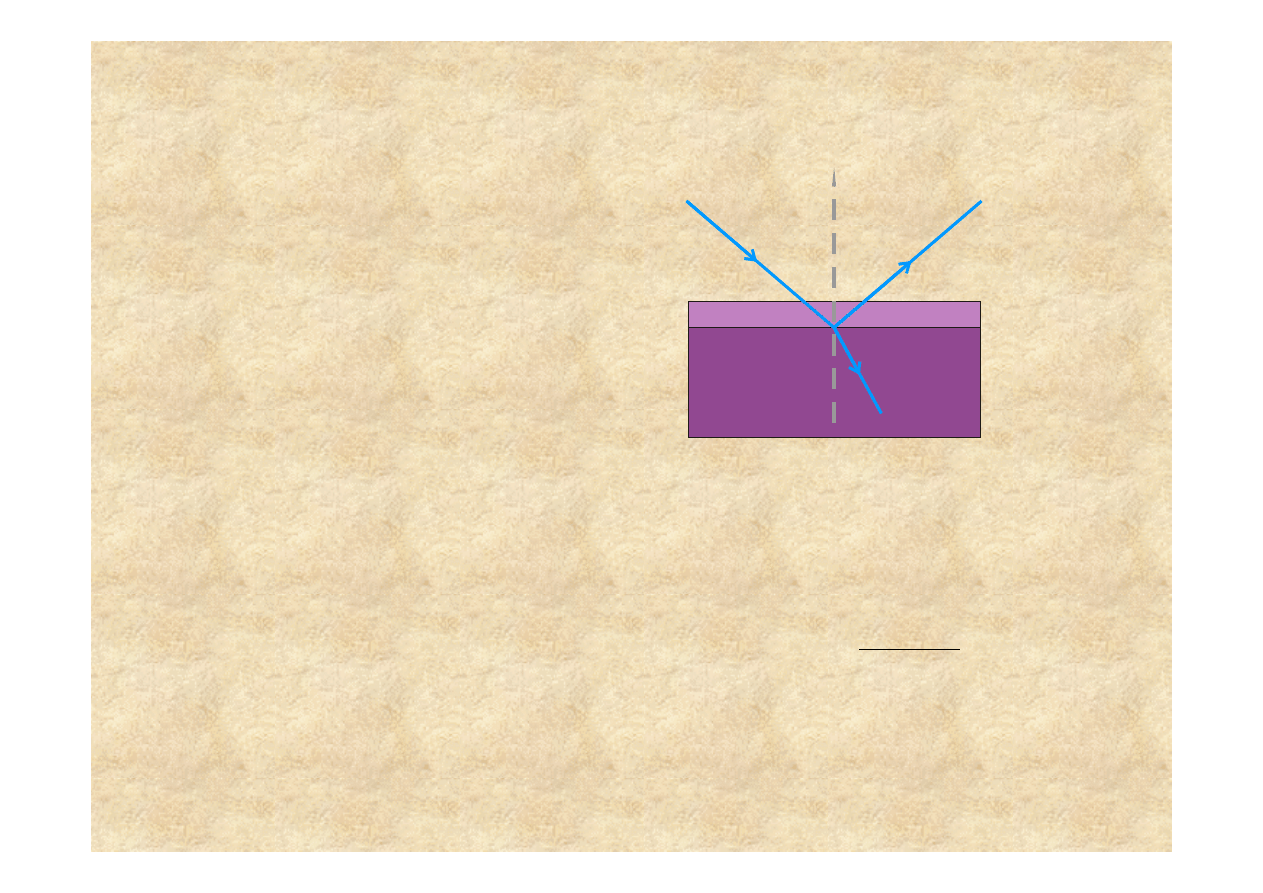
Spektroskopia odbiciowa

Nat

ęż

enie wi

ą

zki odbitej od powierzchni

materiału nieabsorbuj

ą

cego zale

ż

y od

wła

ś

ciwo

ś

ci materiału (współczynnika

załamania), długo

ś

ci fali, stanu

polaryzacji promieniowania padaj

ą

cego

oraz k

ą

ta padania (równania Fresnela).

W przypadku materiałów absorbuj

ą

cych

wi

ą

zka odbita od powierzchni ulega

dodatkowemu osłabieniu w wyniku

absorpcji promieniowania przez

cz

ą

steczki znajduj

ą

ce si

ę

blisko

powierzchni.

I ( )

0

ν

I( )

ν

Wzgl

ę

dne nat

ęż

enie wi

ą

zki

odbitej charakteryzuje
współczynnik odbicia, R(

ν

,

θ

).

Widmo odbiciowe

- wykres zale

ż

no

ś

ci R = f(

ν

,

θ

=const)

( ) ( )

( )

ν

θ

ν

θ

ν

0

,

,

I

I

R

=

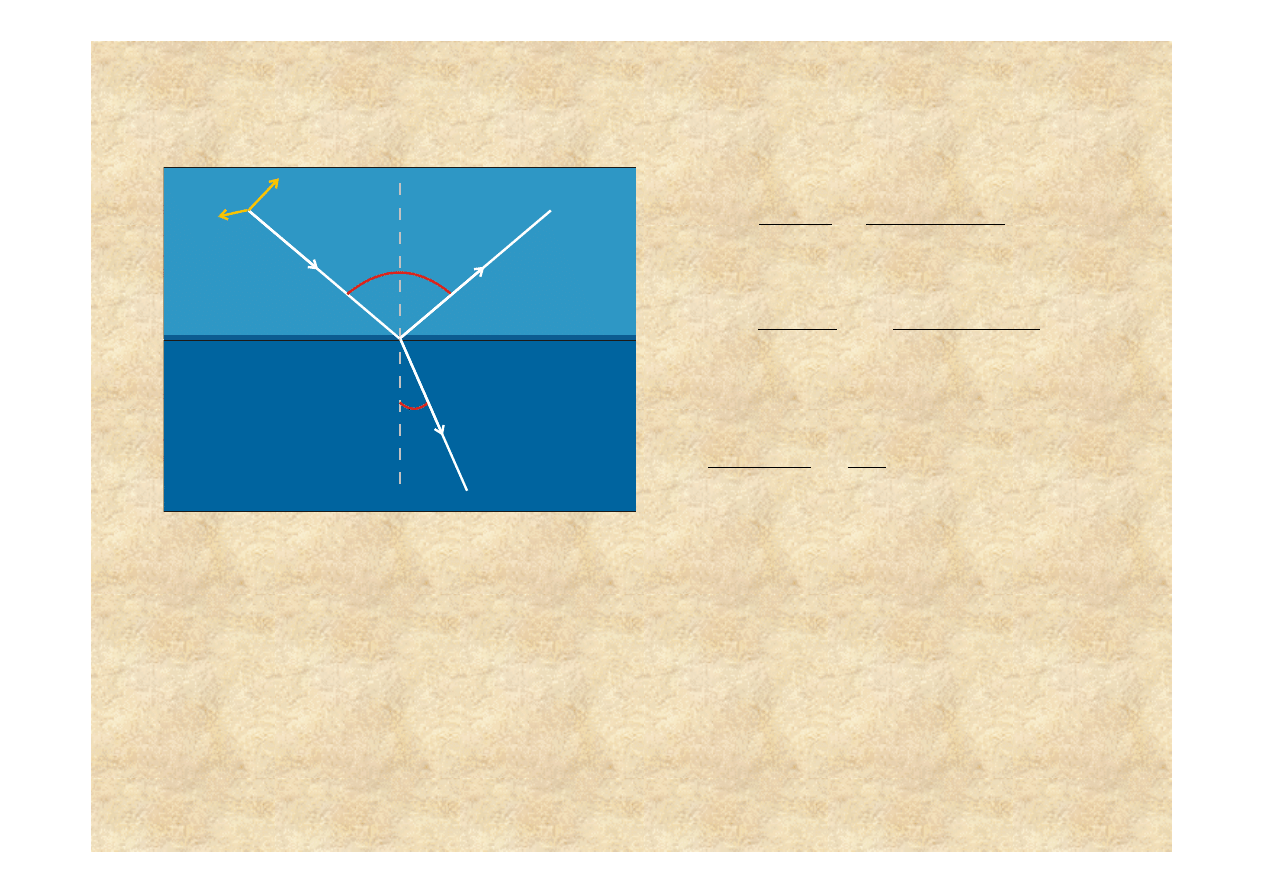
Równania Fresnela

n

1

n

2

θ

1

θ

1

θ

2

E

⊥

E

||

(

)

(

)

2

1

2

1

||

,

0

||

,

||

tg

tg

θ

θ

θ

θ

+

−

=

=

E

E

r

odb

(

)

(

)

2

1

2

1

,

0

,

sin

sin

θ

θ

θ

θ

+

−

−

=

=

⊥

⊥

⊥

E

E

r

odb

Reflektancja:

2

||

||

r

R

=

2

⊥

⊥

=

r

R

Współczynniki refrakcji (załamania):

||

||

1 R

T

−

=

⊥

⊥

−

=

R

T

1

( )

( )

1

2

2

1

sin

sin

n

n

=

θ

θ

(prawo Sneliusa)

Współczynniki odbicia s

ą

funkcj

ą

n,

λλλλ

oraz

θθθθ

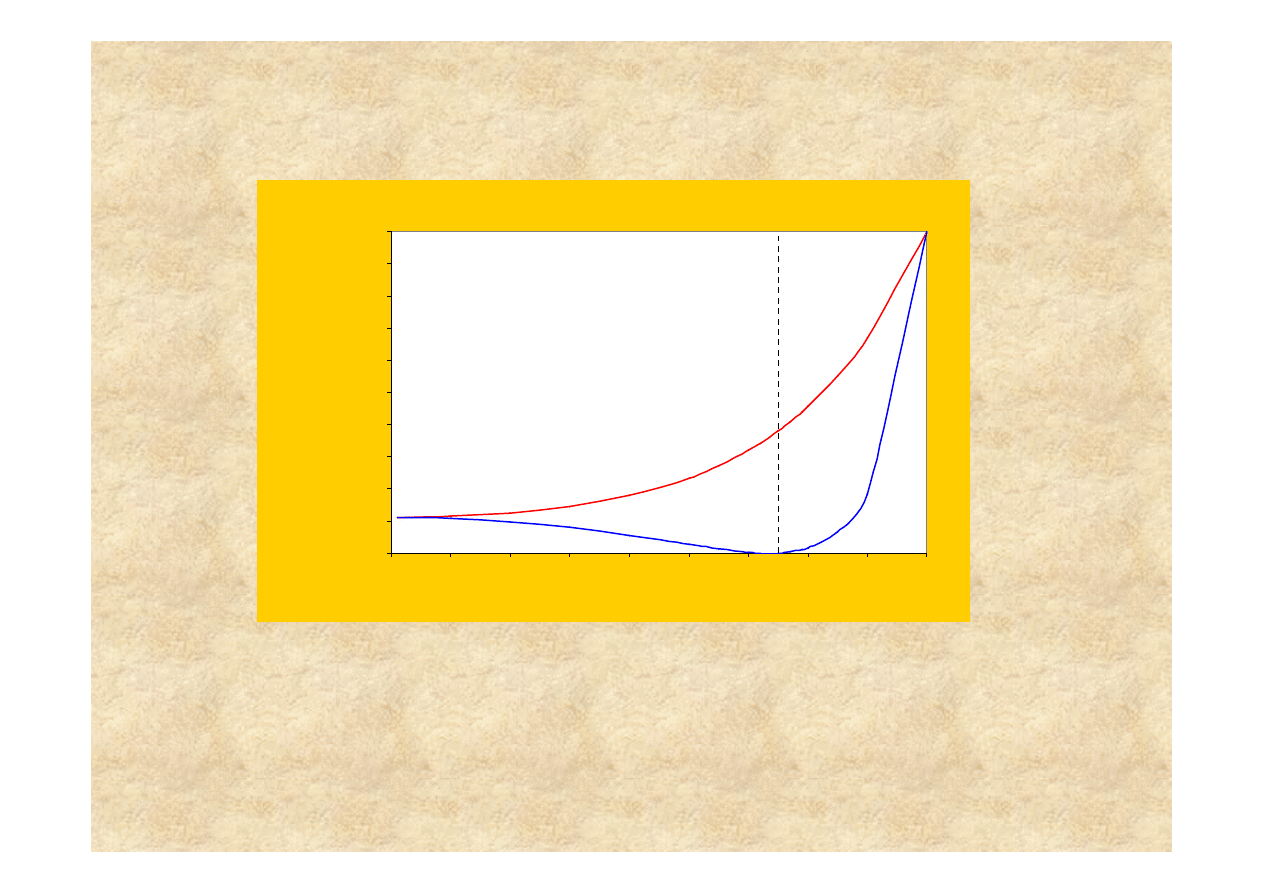
Du

ż

e nat

ęż

enie

ś

wiatła odbitego uzyskujemy stosuj

ą

c du

ż

e warto

ś

ci k

ą

ta

padania promieniowania na powierzchni

ę

próbki (bliskie 90°, promie

ń

„

ś

lizga

si

ę

” po powierzchni).

0

10

20

30

40

50

60

70

80

90

100

0

10

20

30

40

50

60

70

80

90

K

ą

t padania

θ

θ

θ

θ

W

s

p

ó

łc

z

y

n

n

ik

o

d

b

ic

ia

R

(

%

)

R

⊥

⊥⊥

⊥

R

||||||||

n

1

=1, n

2

=2

k

ą

t

B

re

w

s

te

ra

Przej

ś

cie z o

ś

rodka o małej g

ę

sto

ś

ci optycznej do o

ś

rodka o wi

ę

kszej

g

ę

sto

ś

ci optycznej (n

1

< n

2

)

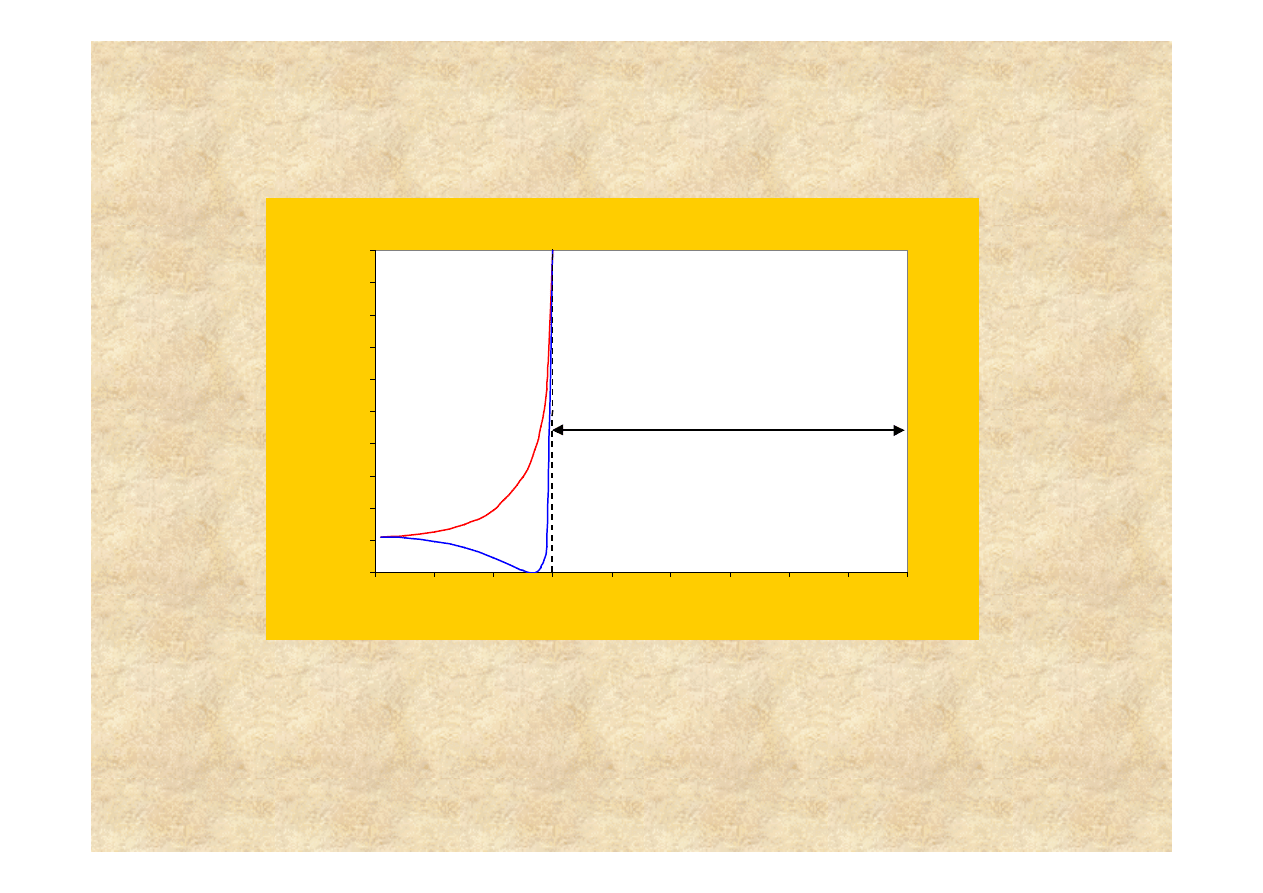
0

10

20

30

40

50

60

70

80

90

100

0

10

20

30

40

50

60

70

80

90

K

ą

t padania

θ

θ

θ

θ

W

s

p

ó

łc

z

y

n

n

ik

o

d

b

ic

ia

R

(

%

)

R

⊥

⊥⊥

⊥

R

||||||||

n

1

=2, n

2

=1

całkowite wewnętrzne odbicie

Du

ż

e nat

ęż

enie odbitego promieniowania uzyskuje si

ę

wykorzystuj

ą

c

zjawisko całkowitego wewn

ę

trznego odbicia.

Przej

ś

cie z o

ś

rodka o du

ż

ej g

ę

sto

ś

ci optycznej do o

ś

rodka o mniejszej

g

ę

sto

ś

ci optycznej (n

1

> n

2

)

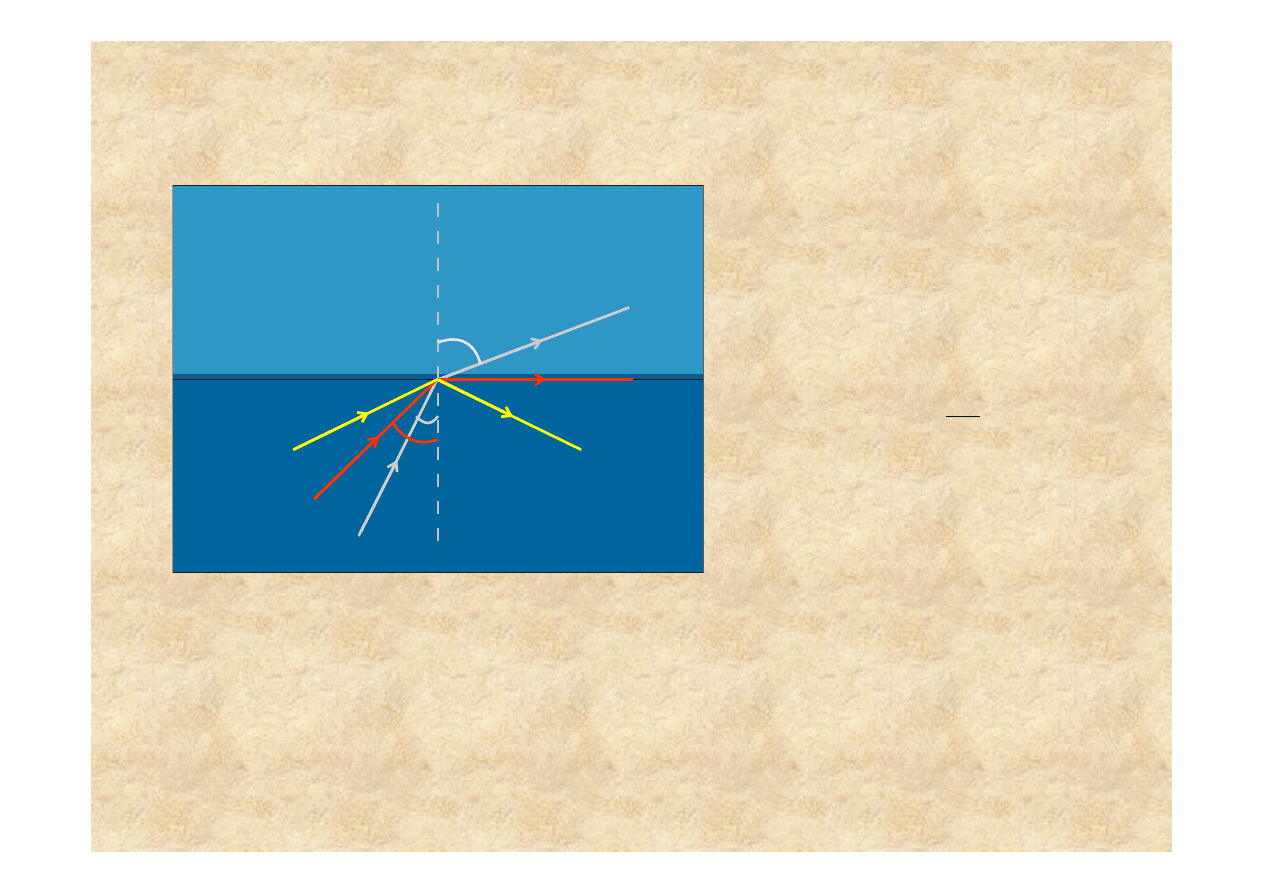
Całkowite wewn

ę

trzne odbicie

n

1

n

2

θ

1

θ

2

θ

k

θ

k

- krytyczny k

ą

t całkowitego

wewn

ę

trznego odbicia

Zjawisko całkowitego wewn

ę

trznego odbicia wykorzystuje si

ę

w metodzie ATR (Attenuated Total Reflection)













=

1

2

sin

arc

n

n

k

θ

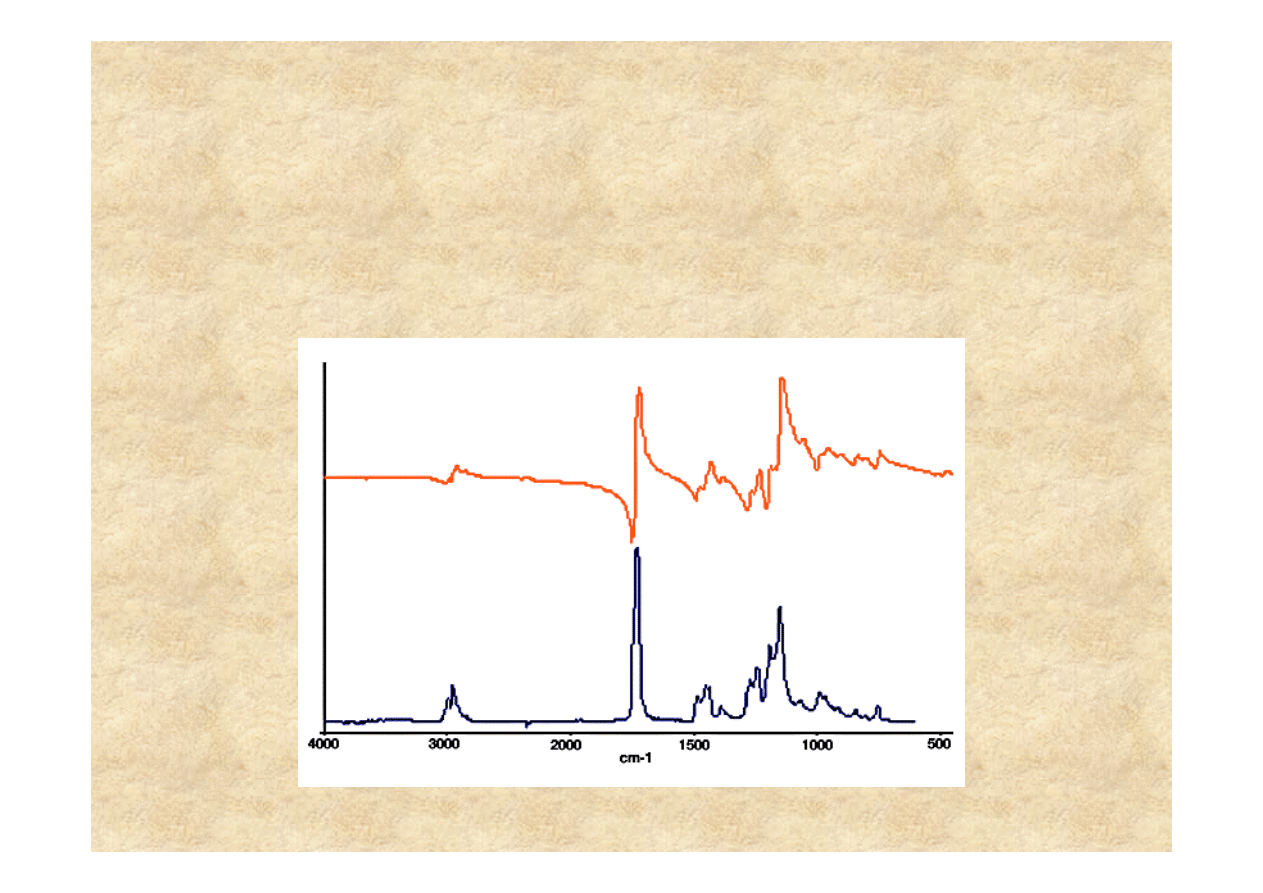
Mierzona reflektancja jest funkcj

ą

m.in. współczynnika załamania

ś

wiatła

materiału, który z kolei zale

ż

y od długo

ś

ci fali promieniowania padaj

ą

cego

(dyspersja)

⇒

obecne w widmie odbiciowym pasma absorpcyjne s

ą

zdeformowane poprzez zale

ż

no

ść

n = f(

ν

)

Ogólna charakterystyka widma odbiciowego

widmo odbiciowe

widmo transmisyjne

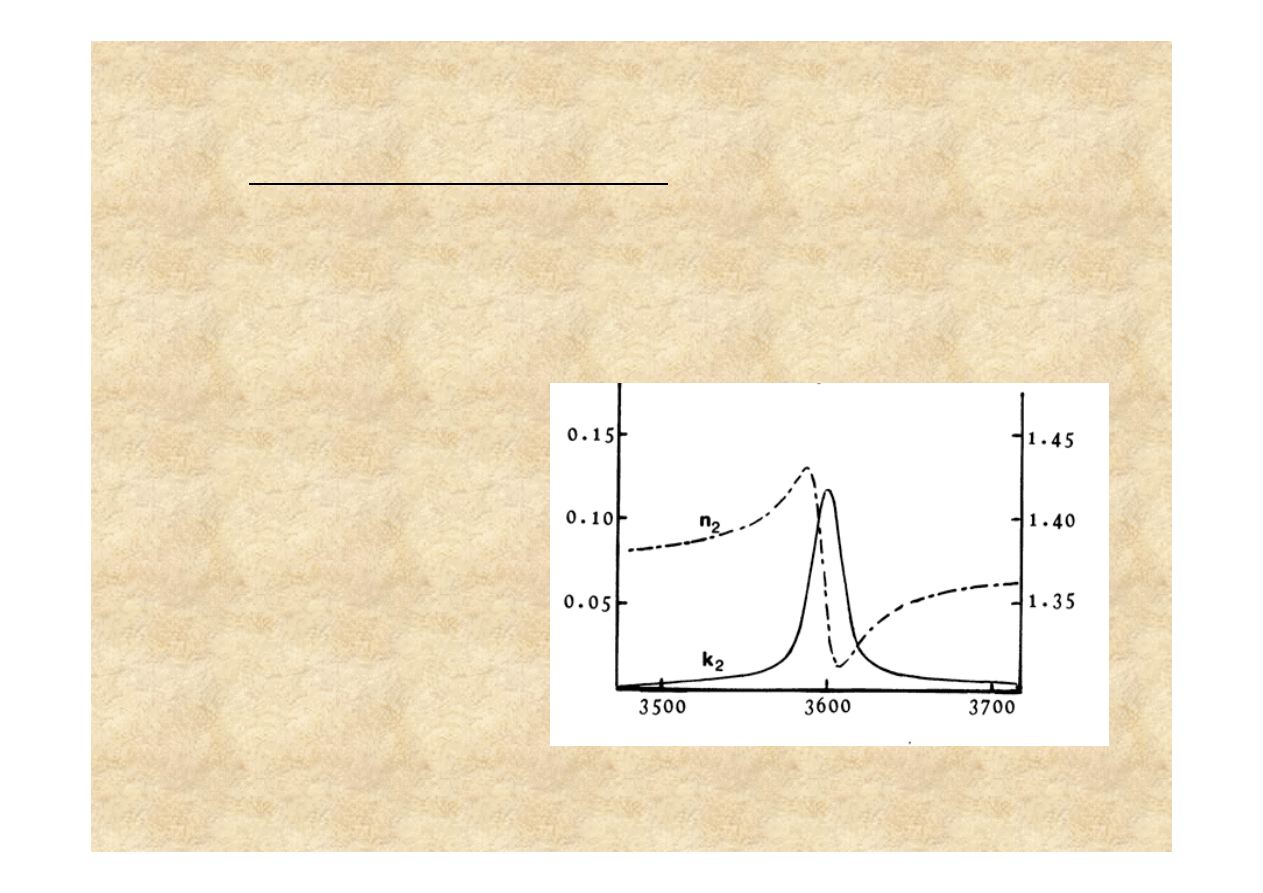
W przypadku materiałów absorbuj

ą

cych, refrakcj

ę

na granicy o

ś

rodków

opisuje zespolony współczynnik załamania dany wyra

ż

eniem:

ik

n

n

−

=

ˆ

n - współczynnik załamania

k - współczynnik ekstynkcji

cm

-1

W obszarze cz

ę

sto

ś

ci

rezonansowej (tzn.

absorbowanej przez próbk

ę

)

warto

ść

współczynnika

załamania zmniejsza si

ę

skokowo ze wzrostem

cz

ę

sto

ś

ci -

anomalna dyspersja

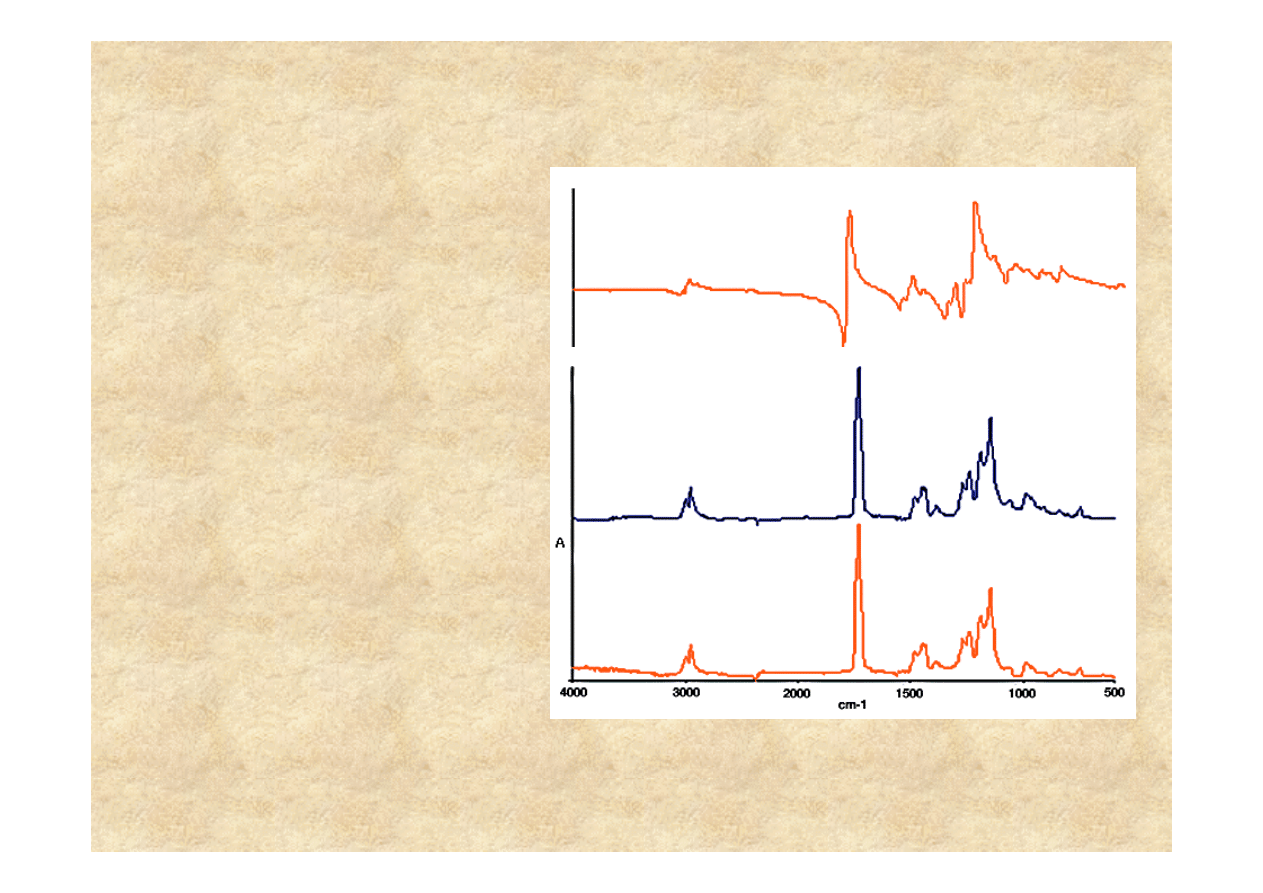
widmo odbiciowe

widmo transmisyjne

widmo odbiciowe
skorygowane

Uzyskanie z widma

odbiciowego informacji

o pasmach absorpcyjnych

wymaga poddaniu go

matematycznej obróbce,

polegajacej na usuni

ę

ciu

z widma efektów

dyspersyjnych (transformacja

Kramersa-Kroniga).

Jak z widma odbiciowego uzyska

ć

widmo transmisyjne?