4.
M
eto
da prz
ekr
ojó
w
Rittera.
Is
to
t�
t
ej
m
et
od
y
je
st
ni
ez
al
e�
ne
wyz
na
cz
eni
e
si
�y
w
do
w
ol
ny
m
p
r�
ci
e
kr
at
ow
ni
cy
z
rów
na
ni
a
rów
now
ag
i,
za
wi
era
j�
ce
go
j
ed
n�
nie
w
iadom
�.
P
rz
ec
in
am
y
kr
at
ow
ni
c�
p
rz
ek
ro
je
m
p
rz
ec
ho
dz
�c
ym
pr
ze
z
tr
zy
pr
�t
y,
któr
ych
kie
run
ki
nie
prz
ec
ina
j�
si
�
w
jednym
punkci
e.
Z
trzech
przeci
�ty
ch
pr
�tó
w
z
aws
ze dwa pr
�t
y pr
ze
ci
na
j�
s
i�
w jednym punkci
e. W
ten sposób mo
�e
m
y z
na
le
��
tr
zy pu
nk
ty
, k
tór
e n
az
ywa
m
y
pu
nk
ta
m
i Ri
tt
era
.
W
ie
m
y,
�e
uk
�a
d
si
�
zn
aj
du
je
s
i�
w
ró
w
nowadze,
je
�e
li
m
o�
em
y
us
ta
w
i�
t
rz
y
ró
w
na
ni
a
su
m
y
m
om
en
tó
w
w
sz
ys
tk
ic
h
si
�
uk
�adu
wzgl
�d
em
t
rz
ec
h
dowol
nych punkt
ów (bieg
unów) nie
le
��
cyc
h na jednej prostej
.
Aby
otrzyma
�
rów
na
nie,
w
którym
wyst
�pi
�a
by
tyl
ko
j
ed
na
ni
ewi
ad
om
a,
ob
li
cza
m
y
su
m
�
m
om
en
tó
w
w
sz
ys
tki
ch
si
�
dz
ia
�a
j�
cyc
h
na
jed
na
cz
���
od
ci
�t
ej
k
rat
own
icy
(l
ew
�
lub
praw
�)
wz
gl
�de
m
punkt
u
Ritt
era.
W
pr
zypad
ku,
gdy
dwa
z
trze
ch
pr
�tó
w
pr
zec
i�
ty
ch
s
�
równ
ol
eg
�e,
to
jeden
punk
t
R
it
te
ra
z
na
jd
uj
e
si
�
w
n
ie
sko
�cz
ono
�ci
. Aby
wy
znac
zy
�
si
��
w
p
r�
ci
e
nie
rów
no
leg
�ym
do
dwó
ch
po
zos
ta
�ych,
stosu
jem
y
równanie
rzutów
ws
zystkich
si
� dz
ia
�a
j�
cyc
h na odci
�t
� cz
��
� kratownicy na
kierunek prostopad
�y d
o d
wó
ch
pr
�t
ów ró
wnoleg
�ych
.
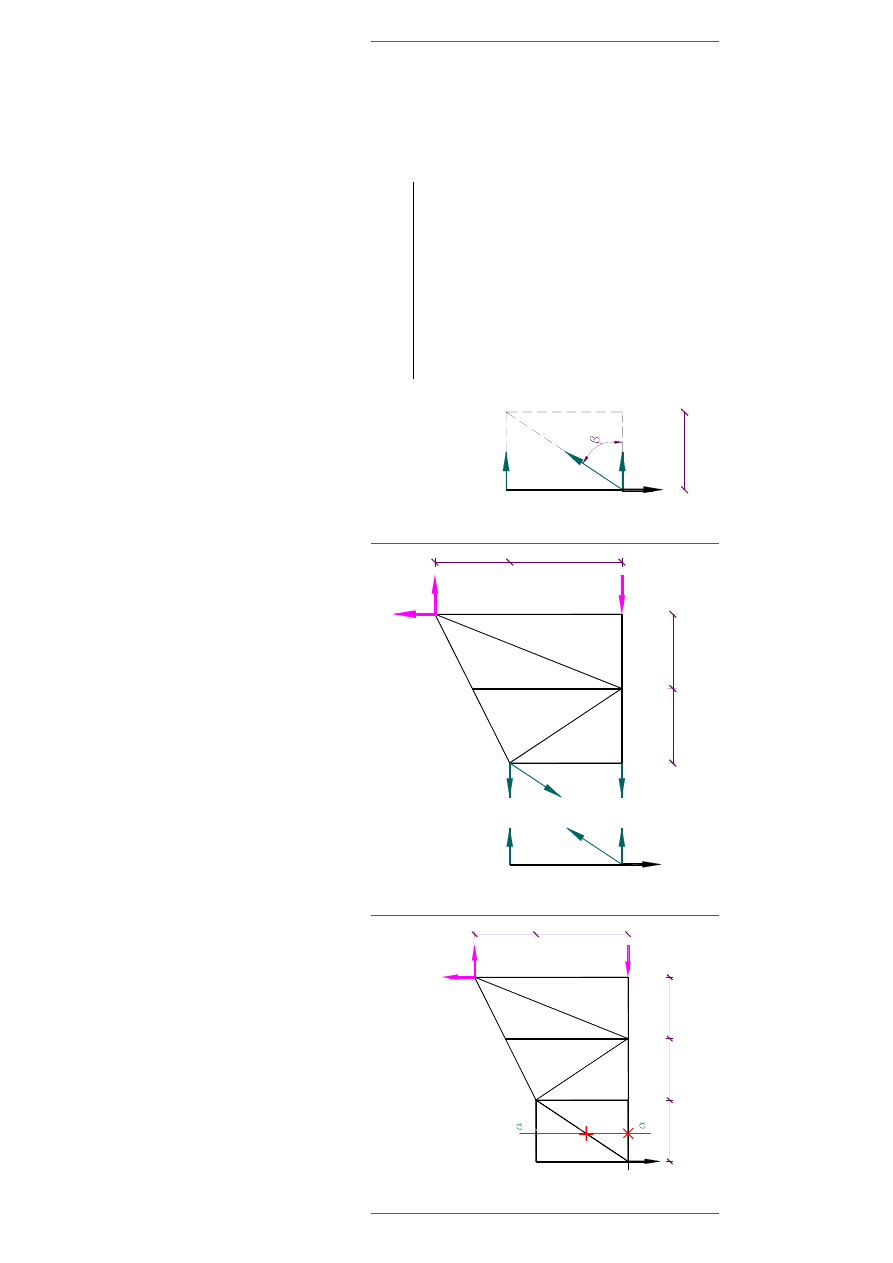
4.1.Przekrój
�
� .
O
blicz
enie wa
rto
�c
i s
i�
w
za
zn
ac
zo
ny
ch p
r�
ta
ch k
rat
ow
nicy
ED
, EG
Ry
s.
17
2.0
24
K
N
3.0
24
K
N
D
20
K
N
E
F
2.
0
G
2.
0
H
C
2.
0
20
K
N
A
B
Rys
.17
20
K
N
20
K
N
2.
0
2.
0
E
F
D
G
C
H
2.0
3.0
24
K
N
B
24
K
N
A
N
FG
N
E
G
N
GF
N
GE
N
DE
N
E
D
Rys
.18
N
F
G
20
K
N
E
F
N
E
D
N
E
G
2.
0
D
G
Rys
.19
Lew
a
cz
��
�
kr
ato
wn
ic
y
Rys
.18
,
Rys
.19
�
M
G
= 0
20
2 N
E
D
3
=
0
�
N
E
D
=
13.333
�
Z = 0
Pu
nkt
R
it
te
ra
zn
aj
duj
e
si
�
w
ni
esk
o�
cz
on
o�
ci
.
N
E
G
s
in
�
20 =
0
�
N
E
G
=
24
.0
37
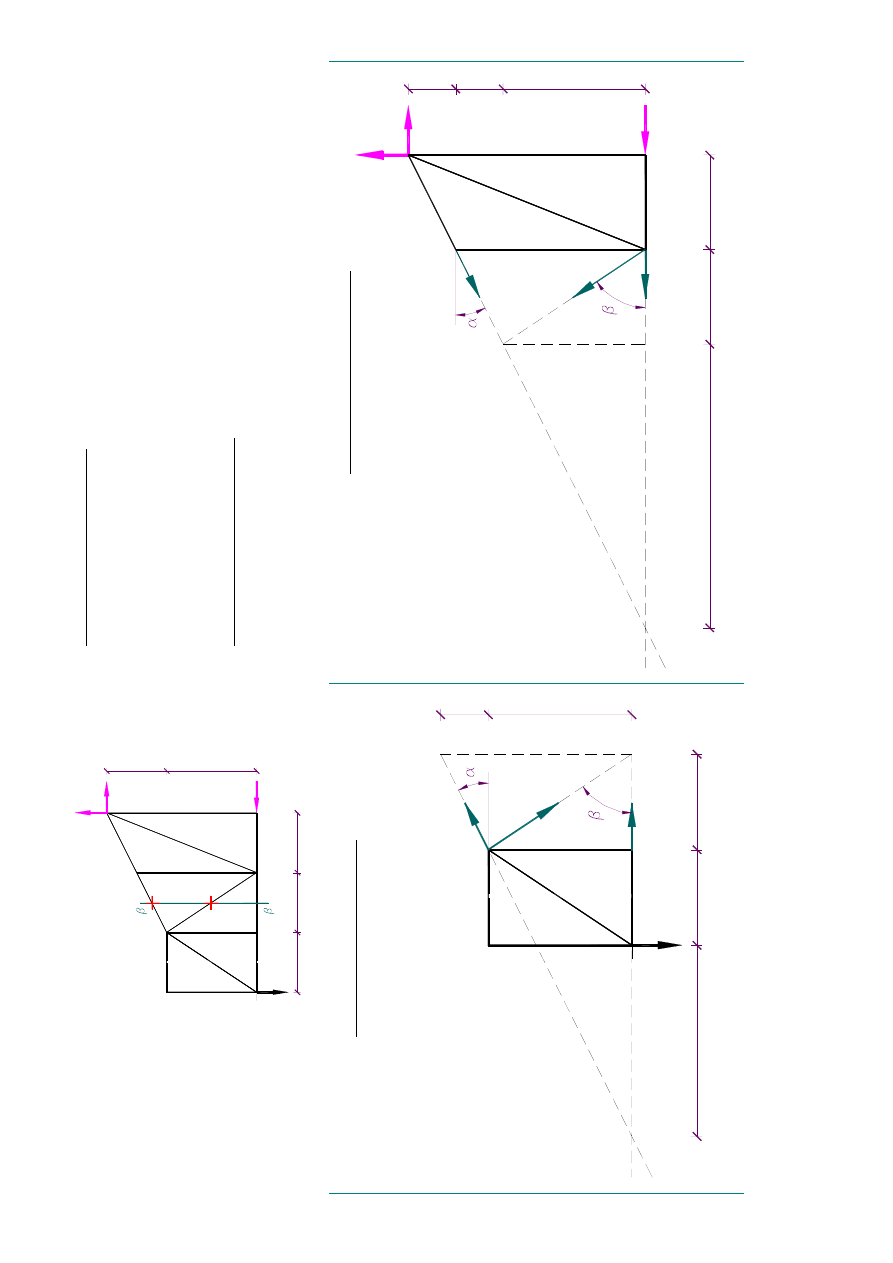
4.
2. Pr
ze
krój
�
�. Oblic
zeni
e warto
�c
i s
i�
w
za
zn
acz
on
ych
p
r�
tach
k
rato
wnic
y
GH
, GC
Ry
s.2
0
____________________________________________________________________________________________________________________________
htt
p://
riad.usk.
pk.edu.p
l/~iwro
blew/dy
daktyka
9/11
20
K
N
F
E
24
K
N
3.0
24
K
N
2.0
D
2.
0
G
2.
0
C
H
20
K
N
2.
0
A
B
Rys
.20
Lew
a
cz
��
�
krato
wni
cy
Ry
s.2
1
�
M
C
= 0
N
GH
c
os
�
3 + N
GH
si
n
�
2 20
4 = 0
�
N
GH
=
22
.3
62
�
M
I
= 0
N
GC
c
os
�
3 +
N
GC
s
in
�
6 +
20
4 =
0
�
N
GC
=
12.018
P
ra
w
a
cz
��
�
kr
at
ownicy
Rys.
22
�
M
I
= 0
N
C
G
si
n
�
8
+
24
5
20
10
=
0
�
N
C
G
=
12.018
Lew
a
cz
��
�
krato
wn
icy
20
KN
E
2.0
D
F
H
C
2.
0
G
1.0
3.0
N
G
H
N
G
C
N
D
C
I
d
=
4.
0
Rys
.21
P
ra
w
a
cz
��
�
krato
wnic
y
24
K
N
24
K
N
C
H
2.0
G
20
K
N
2.
0
B
A
3.0
1.0
I
6.
0
N
H
G
N
C
G
N
C
D
1.0
D
Rys
.22
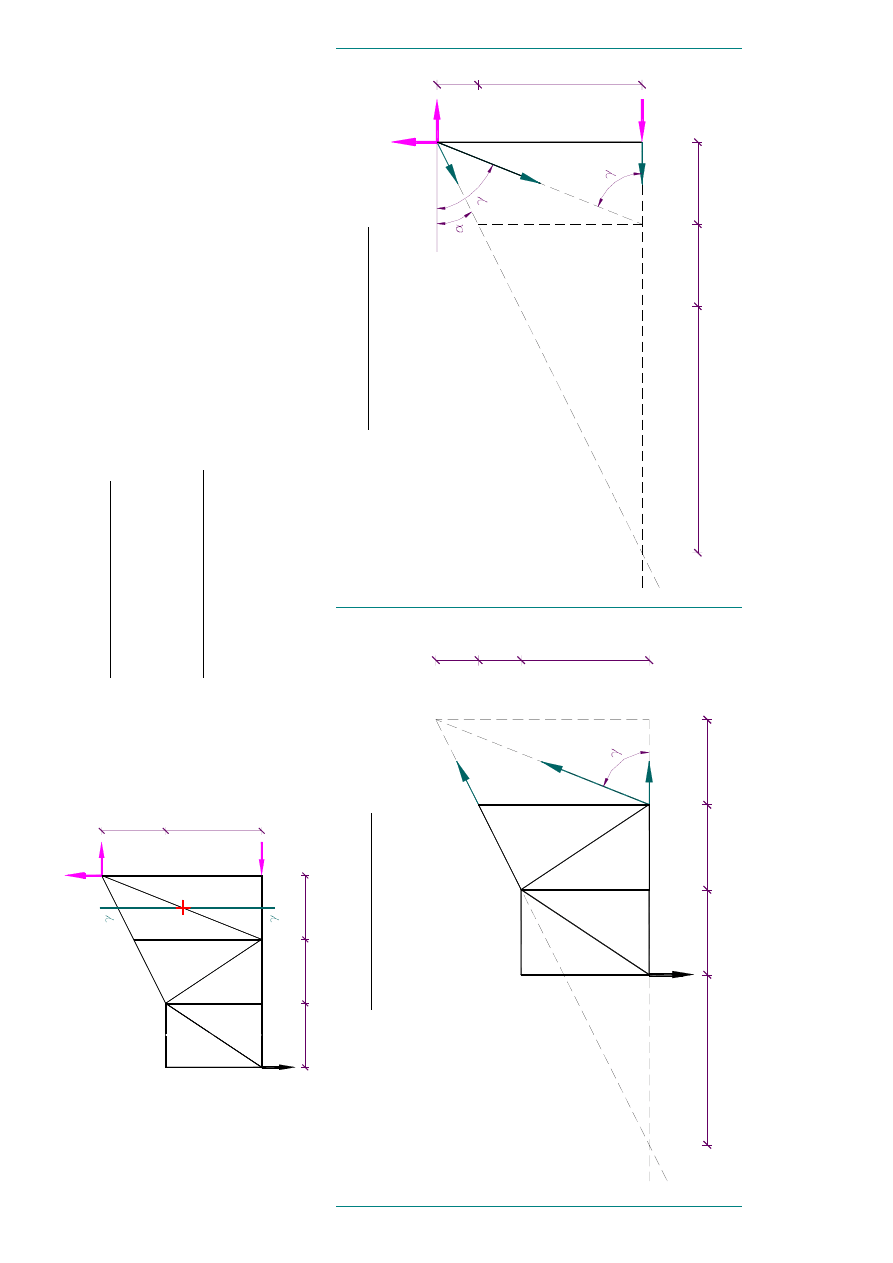
4.
3. Pr
ze
krój
�
� . Ob
lic
ze
ni
e w
ar
to
�c
i s
i�
y
w za
znaczony
m p
r�
cie kratownicy CA
Rys
.23
____________________________________________________________________________________________________________________________
htt
p://
riad.usk.
pk.edu.p
l/~iwro
blew/dy
daktyka
10/11
20
KN
E
F
2.
0
24
KN
24
KN
H
C
2.
0
D
G
20
K
N
2.
0
B
A
2.0
3.0
Rys
.23
Lew
a
cz
��
�
krato
wn
icy
Ry
s.2
4
�
M
I
= 0
N
C
A
si
n
�
8
+
20
4
=
0
�
N
C
A
=
10.77
P
ra
w
a
cz
��
�
kr
at
ownicy
Rys.
25
�
M
I
= 0
N
AC
si
n
� 10 N
AC
c
os
�
5
+
2
4
5
20
10
=
0
�
N
AC
=
10.77
Lew
a
cz
��
�
krato
wn
icy
I
N
H
A
3.0
N
C
B
N
C
A
1.0
1.0
D
20 K
N
E
2.0
2.0
C
2.0
B
F
G
H
A
4.0
Rys
.24
P
ra
w
a
cz
��
�
krato
wnic
y
I
6.0
24
K
N
24
K
N
C
2.
0
N
AH
20
K
N
2.
0
B
A
1.0
4.0
N
B
C
N
AC
H
C
Rys
.25
____________________________________________________________________________________________________________________________
htt
p://
riad.usk.
pk.edu.p
l/~iwro
blew/dy
daktyka
11/11
Wyszukiwarka
Podobne podstrony:
Kratownica przyk
Kratownica trzykrotnie statycznie niewyznaczalna
K8 kratownice K4
kratownica belka 57
Cegła kratówka i?ny 09
Projekt 2 kratownica 2 poprawiona
przyk adowa bibliografia II
KOZ (Cw) Cwiczenie 10 Przyk A3 id 249078
Projekt Inzynierski Obliczenia wiązara kratowego G3 mitek
kratownica tabele
kol1 przyk zad
CBS podr przyk pl 2010
Łączenie drewna w kratownicach dachowych płytkami perforowanymi czy sklejką
kratownica A2 2
więcej podobnych podstron