Wydział
Nr zespołu
Imię i nazwisko
Pkt przyg.
Kierunek
Nr ćwiczenia
Tytuł ćwiczenia
Wyznaczanie naprężeń za pomocą tensometru
oporowego
Pkt spraw.
Grupa
Data
Pkt koń.
Wstęp
Tensometr - czujnik, służący do pomiaru. Tensometry wykorzystuje się również pośrednio do
pomiaru innych wielkości nieelektrycznych (np. siły, naprężenia, ciśnienia, drgań). W
praktyce pomiar tensometryczny wielkości innych, niż wydłużenie, polega na pomiarze
wydłużenia i obliczeniu badanej wielkości w oparciu o przyjęty związek fizyczny między tą
wielkością a wydłużeniem (np. dla określenia naprężenia wykorzystuje się prawo Hooke'a).
Najczęściej stosowanym rodzajem tensometrów są tensometry oporowe, zmieniające swoją
rezystancję wraz ze zmianą wymiarów. Ze względu na budowę rozróżnia się tensometry
oporowe: wężykowe, zygzakowe, kratowe, foliowe. Ze względu na materiał użyty do budowy
tensometry mogą być metaliczne lub półprzewodnikowe.
Zasada działania
W tensometrii elektrooporowej wykorzystuje się zjawisko zmiany oporności elektrycznej
przewodnika wynikającej z jego wydłużenia lub skrócenia. Zależność opisuje wzór:
gdzie: ρ - jest opornością właściwą (rezystywnością) materiału przewodnika;
L - długość przewodnika;
A - pole przekroju
Z powyższego wzoru wynika zależność na względny przyrost oporności:
gdzie: ΔR - przyrost oporności;
α - stały współczynnik zależny od materiału, (typowa wartość 2);
ε – odkształcenie
Na podstawie odkształceń, korzystając z uogólnionego prawa Hooke'a można wyznaczyć
naprężenia.
Mostek Wheatstone’a
Do pomiaru oporu stosujemy obwód elektryczny zwany mostkiem Wheatstone'a.
W jedną gałąź mostka włączamy tensometr
"czynny" R
1
, w drugą, jako opór znany, taki
sam tensometr, przyklejony takim samym
klejem, na takim samym podłożu, tzw.
tensometr
kompensacyjny
R
2
.
Postępowanie to ma na celu:
a) wyeliminowanie wpływu temperatury na
opór tensometru, wpływu na ogół silniejszego
niż wpływ naprężeń mechanicznych.
Jeżeli przez galwanometr prąd nie płynie, to ten
sam prąd płynie przez oba tensometry i podnosi
jednakowo ich temperaturę;
b) wyeliminowanie zmiany oporu tensometru, spowodowanej skurczem kleju
.
Pozostałe opory: R
3
i R
4
- każdy z nich jest sumą oporu
Ro
i oporu odcinka drutu oporowego: odpowied-
nio
AB
i
BC.
Drut oporowy jest rozpięty wzdłuż skali milimetrowej i posiada znany opór
Rs.
Pomiary i obliczenia
Celem naszego ćwiczenia jest wyznaczenie naprężeń ciała stałego – stalowego pręta, dla
różnych obciążeń- 1kg, 2kg. Najpierw podłączamy obwód i zaczynamy pomiar gdy
płaskownik leży na stole i jest nie obciążony. Po zamknięciu obwodu, sterując ruchomym
suwakiem B, staramy się by galwanometr wyświetlał wartość równą zero, czyli by prąd
przepływający przez niego
Ig
=
O
.
Równowaga powinna nastąpić przy położeniu suwaka w pobliżu
środka drutu
AC.
Początkowe położenie styku w naszych obliczeniach wynosi :
x
0
= 42,16 cm
Następnie poddajemy nasz materiał odkształceniom. W tym celu mocujemy go w uchwycie.
W skutek tego, że zmienia się opór tensometru, przyklejonego do stalowego, odkształcanego
płaskownika o ∆R
1
, równowaga mostka zostaje zakłócona i pojawia się prąd
I
g
≠
O płynący przez
galwanometr. Następnie staramy się ponownie uzyskać równowagę, czyli przesuwamy ponownie
suwak B do położenia x
w
. Przy
I
g
=
O
zostaje spełniona proporcja:
gdzie
oznacza opór odcinka drutu oporowego długości: ∆x = x
1
– x
0
. Można go obliczyć ze wzoru
mając opór całkowity drutu R
5
i jego długość (L = 1,000 m):
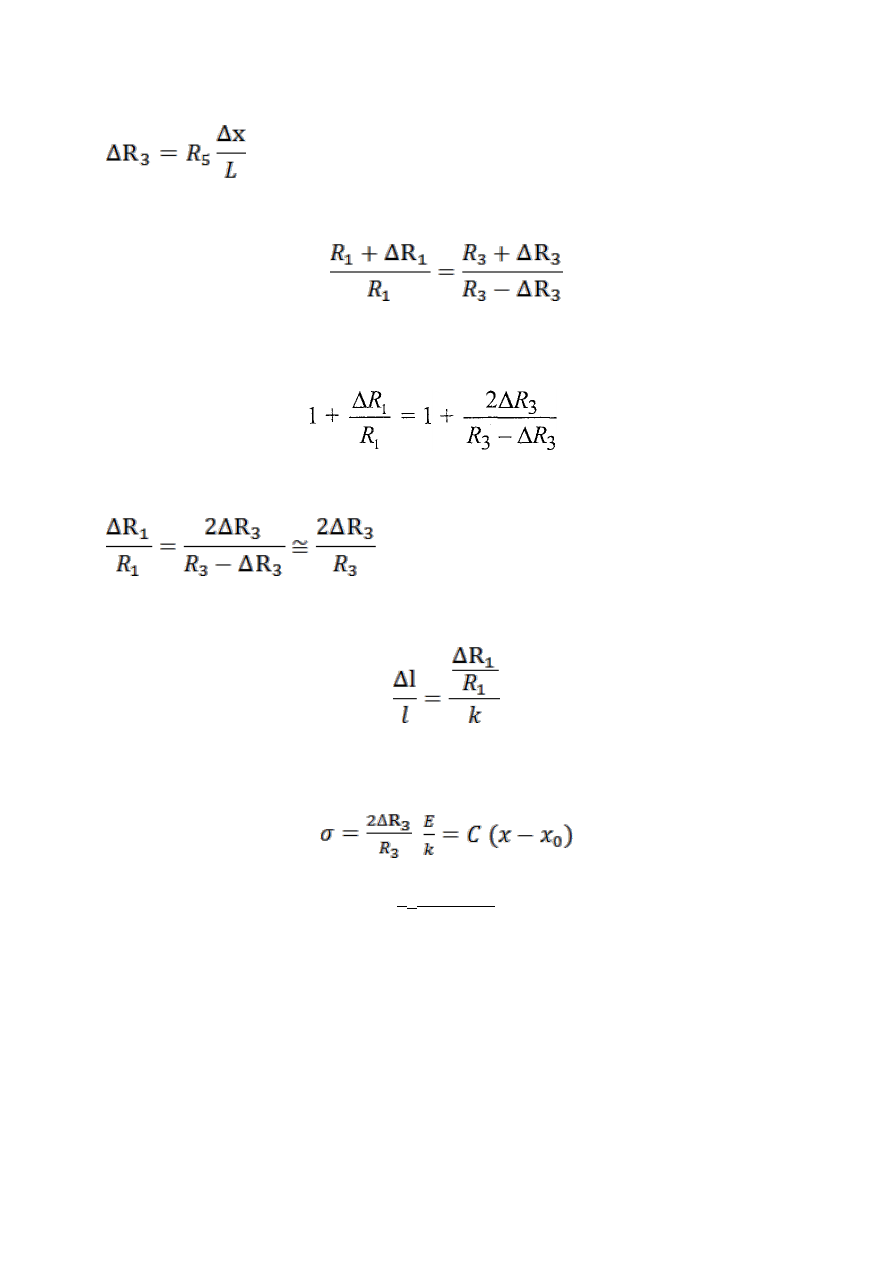
Przy założeniu, że: R
1
= R
2
,
R
3
=
R
4
=
R
0
+
1/2 R
5
,
równanie nasze przybierze postać:
Po dalszych przekształceniach:
stąd przy założeniu, że
∆R3 «R
3
dostajemy:
Ze wzorów wynika ze wydłużenie względne tensometru czynnego jest proporcjonalne do względnej
zmiany jego oporu:
Po przekształceniu i podstawieniu powyższych wzorów otrzymujemy ostateczny wzór na naprężenie
mierzone tensometrem:
.
Obciążenie własne belki:
x
w
=48,3 cm
Następnie po uzyskaniu równowagi zamocowanego płaskownika o długości L=1,000m
obciążamy go odważnikami o masie 1kg i 2kg. Nasz materiał ma wyznaczone 7 położeń x co
10cm. Na każdym z nich po kolei umieszczamy odważniki, po czym ustawiamy galwanometr
w stan równowagi przesuwając suwakiem B tak by prąd przez niego przepływający ponownie
był równy zero -
Ig
=
O.
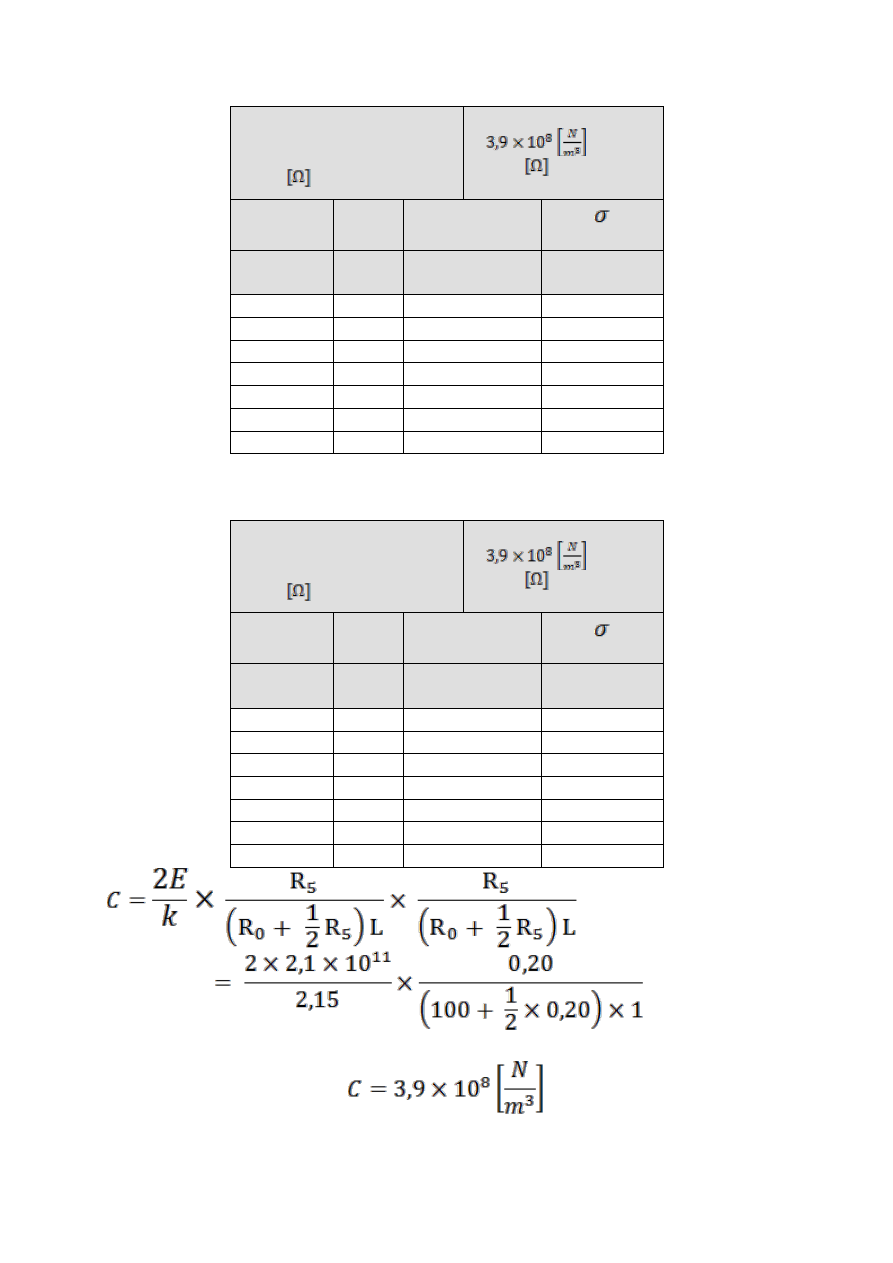
Tabelka z danymi dla obciążenia m
1
=1kg
x
w
=48,3 [cm]
x
0
= 42,16 [cm]
k=2.15
R
0
=100
E= 210 GPa
C=
R
5
=0,20
L=1,000 [m]
r
[m]
x
i
[cm]
∆x
i=
x
i
-x
o
[cm]
[N/m
2
]
obciążenie
własne belki
48,3
6,14
23946000
r
1
= 0,70
50,9
8,74
34086000
r
2
= 0,60
51,9
9,74
37986000
r
3
= 0,50
52,9
10,74
41886000
r
4
= 0,40
53,9
11,74
45786000
r
5
= 0,30
54,9
12,74
49686000
r
6
= 0,20
55,9
13,74
53586000
r
7
= 0,10
56,9
14,74
57486000
Tabelka z danymi dla obciążenia m
2
=2kg
x
w
=48,3 [cm]
x
0
= 42,16 [cm]
k=2.15
R
0
=100
E= 210 GPa
C=
R
5
=0,20
L=1,000 [m]
r
[m]
x
i
[cm]
∆x
i=
x
i
-x
o
[cm]
[N/m
2
]
obciążenie
własne belki
48,3
6,14
23946000
r
1
= 0,70
52,4
10,24
39936000
r
2
= 0,60
54,3
12,14
47346000
r
3
= 0,50
56,4
14,24
55536000
r
4
= 0,40
58,4
16,24
63336000
r
5
= 0,30
60,6
18,44
71916000
r
6
= 0,20
62,5
20,34
79326000
r
7
= 0,10
64,6
22,44
87516000
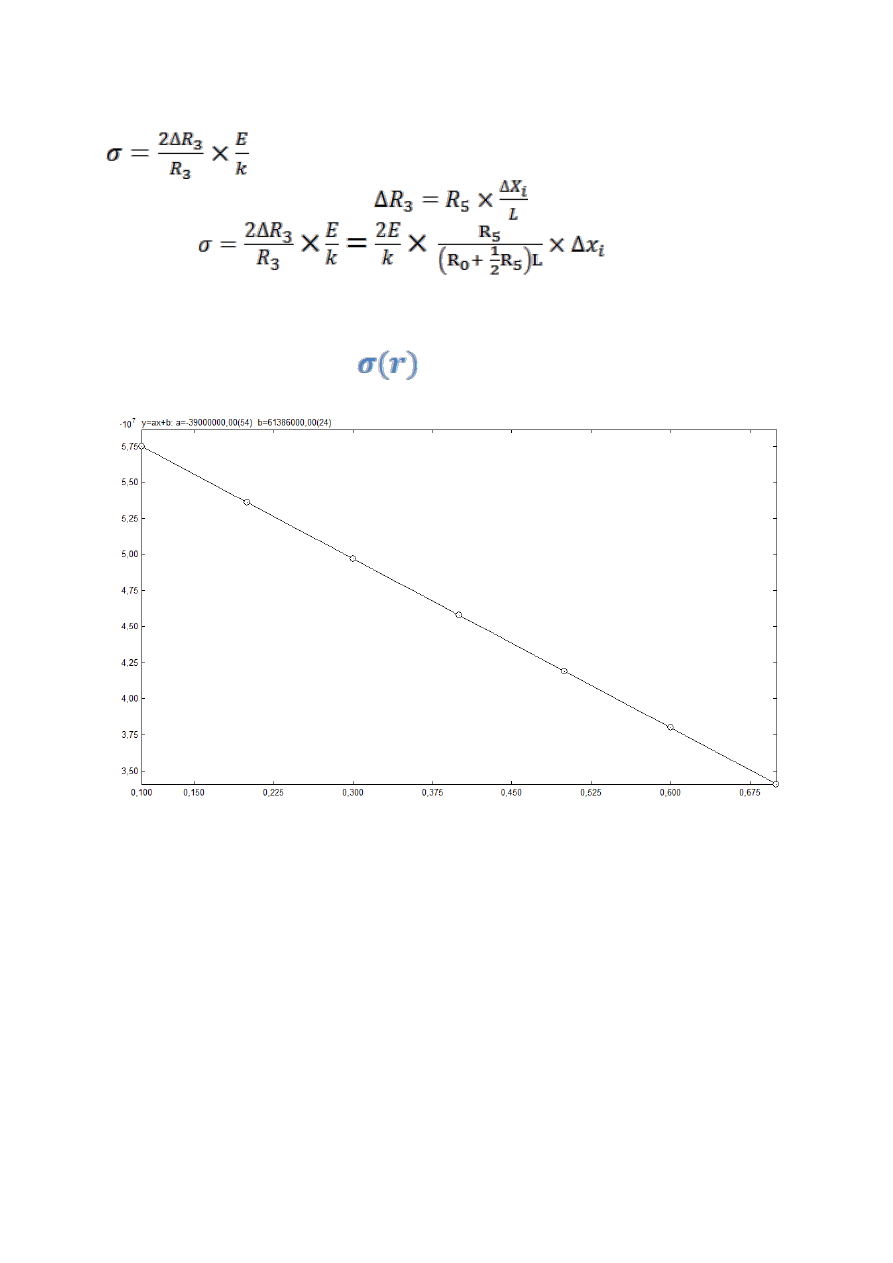
Naprężenia zostały wyliczone ze wzoru:
w którym
R
3
dane jest wyrażeniem
a R
3
= R
4
= R
0
+ 0.5 R
5
, więc
ostatecznie:
Wykresy naprężenia ramienia w funkcji długości
ramienia działania -
dla m
1
dla m
2
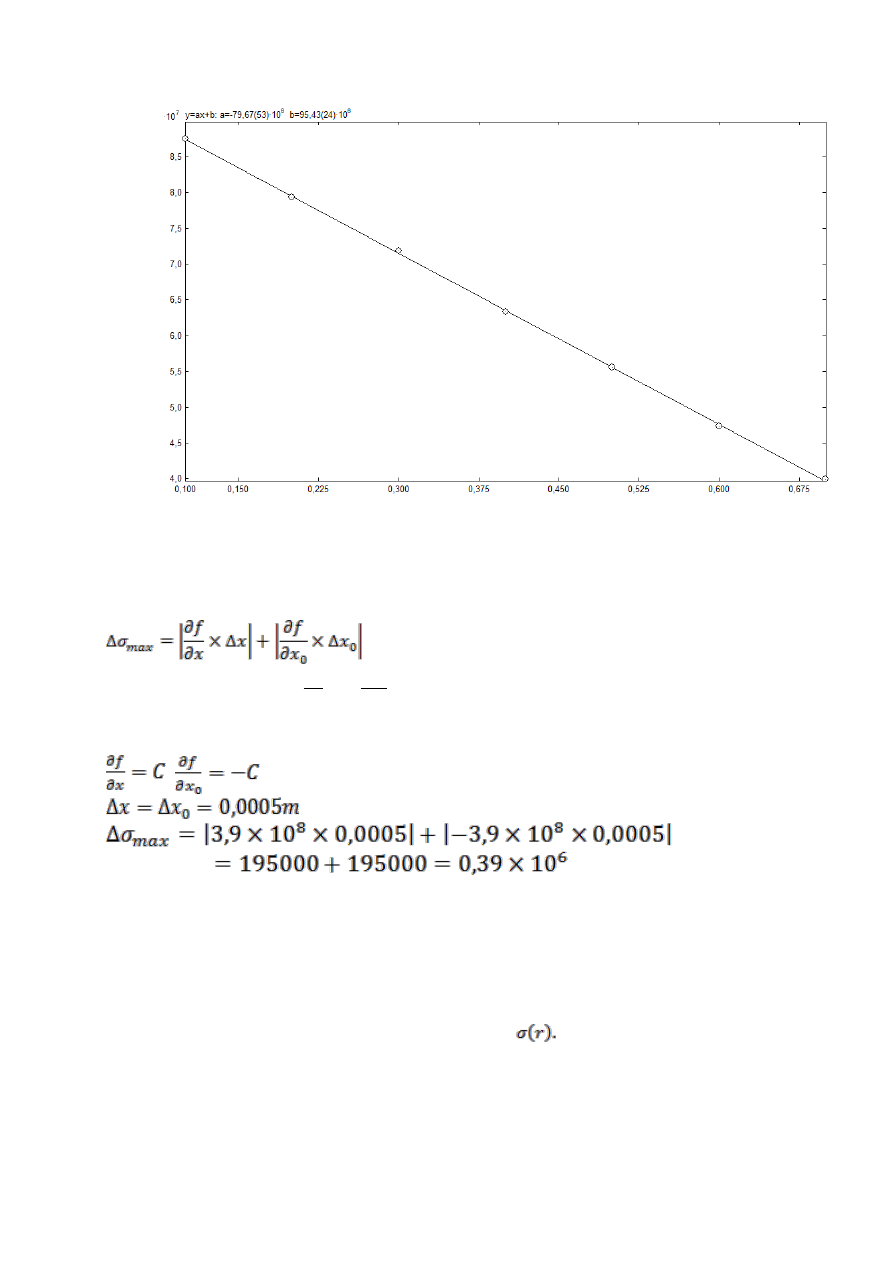
Niepewności pomiarowe dla jednego pomiaru –
np. obciążenie własne belki:
C
x
f
C
x
f
0
,
m
x
x
0005
,
0
0
,
Wnioski:
Nasze wyniki wskazują jednoznacznie na to, że odległość r w jakiej umieszczamy odważnik na
tensometrze jest wprost proporcjonalna do naprężenia powstałego w jego wnętrzu. W miarę
zwiększania odległości od punktu zaczepienia tensometru w uchwycie zwiększa się
naprężenie. Potwierdza to również wykres zależności f=
Trzeba jednak wziąć pod
uwagę, że jak każdy pomiar w tym również ten obarczony jest błędem wynikającym choćby z
różnorodnego odczytania wartości pomiarowych z galwanometru.