UNIWERSYTET TECHNOLOGOCZNO-PRZYRODNICZY

w BYDGOSZCZY

WYDZIAŁ TELEKOMUNIKACJI I ELEKTROTECHNIKI

LABORATORIUM ELEKTROTECHNIKI TEORETYCZNEJ

ZAKŁAD PODSTAW

ELEKTROTECHNIKI

SPRAWOZDANIE Z ĆWICZENIA NR 16

Temat ćwiczenia:

Badanie filtrów reaktancyjnych

Autor sprawozdania: Piotr Zając Grupa ćwiczeniowa 5

Data wykonania ćwiczenia 28.02.2007 r.

Ocena za sprawozdanie

Data przyjęcia sprawozdania …………………….. …………………………

1. Cel ćwiczenia.

Praktyczne zapoznanie się z podstawowymi własnościami elektrycznych filtrów reaktancyjnych typu k.

2. Schemat układu pomiarowego.

3. Schematy badanych filtrów.

1. Filtr dolnoprzepustowy typu ,,T ”.

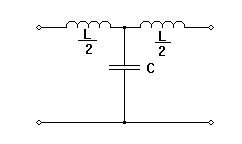
½ L = 5,5 mH

C = 0,4 μF

Ro= 165,8 Ω

b)

Filtr górnoprzepustowy typu ,, Π ”.

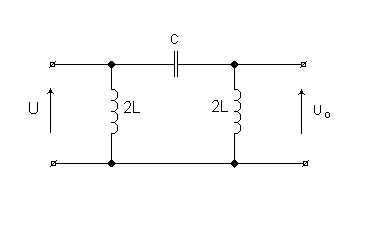
C = 0,05 μF

C=0,05 μF

2L = 11,0 mH

Ro = 331,7 Ω

4. Wzory i przykłady obliczeń.

Współczynnik tłumienia:

a) dla filtra dolnoprzepustowego.

Pulsacja graniczna:

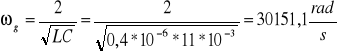
Częstotliwość charakterystyczna:

Impedancja charakterystyczna:

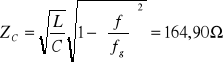
b) dla filtra górnoprzepustowego.

Pulsacja graniczna:

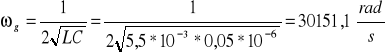
Częstotliwość charakterystyczna:

Impedancja charakterystyczna:

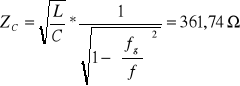
5. Tabela obliczeń:

FILTR DOLNOPRZEPUSTOWY TYPU „T”					FILTR GÓRNOPRZEPUSTOWY TYPU „Π”
f	U	U/U		Z	f	U	U/U		Z
Hz	V	-	dB		Hz	V	-	dB
508	11,08	0,90	-0,89	164,90	502	0,06	166,67	44,44
1006	11,05	0,90	-0,87	162,15	1009	0,25	40,00	32,04
1511	11,18	0,89	-0,97	157,40	1504	0,55	18,18	25,19
2008	11,53	0,87	-1,24	150,61	2006	0,98	10,20	20,18
2505	12,16	0,82	-1,70	141,44	2510	1,51	6,62	16,42
3003	13,31	0,75	-2,48	129,35	3011	2,15	4,65	13,35
3514	14,77	0,68	-3,39	112,93	3504	2,84	3,52	10,93
4022	14,32	0,70	-3,12	90,45	4008	3,63	2,75	8,80
4500	11,28	0,89	-1,05	57,59	4500	4,42	2,26	7,09
5000	7,86	1,27	2,09		5010	5,15	1,94	5,76	1180,76
5520	5,36	1,87	5,42		5510	5,93	1,69	4,54	671,07
6000	3,75	2,67	8,52		6010	6,64	1,51	3,56	552,50
6510	2,77	3,61	11,15		6500	7,30	1,37	2,73	490,80
7000	2,14	4,67	13,39		7050	7,94	1,26	2,00	455,55
7510	1,68	5,95	15,49		7500	8,42	1,19	1,49	431,16
8030	1,34	7,46	17,46		8040	8,62	1,16	1,29	413,65
8530	1,09	9,17	19,25		7500	8,98	1,11	0,93	401,16
9040	0,90	11,11	20,92		9030	9,37	1,07	0,57	391,35
9500	0,77	12,99	22,27		9530	9,68	1,03	0,28	384,29
10020	0,64	15,63	23,88		10050	9,98	1,00	0,02	377,81
10520	0,53	18,87	25,51		10540	10,22	0,98	-0,19	372,70
11010	0,46	21,74	26,74		11000	10,26	0,97	-0,22	368,51
11520	0,39	25,64	28,18		11520	10,31	0,97	-0,27	364,82
12020	0,34	29,41	29,37		12040	9,70	1,03	0,26	361,74

6. Wnioski:

W filtrach dolnoprzepustowych przy małych częstotliwościach reaktancja cewek ωL jest nie duża, a reaktancja kondensatorów przybiera duże wartości, wobec czego prądy o małych częstotliwościach przepływają przez czwórnik. W przypadku dużych częstotliwości reaktancje cewek są duże, a reaktancje kondensatorów, w związku z tym prądy o wielkich częstotliwościach praktycznie nie przechodzą przez czwórnik.

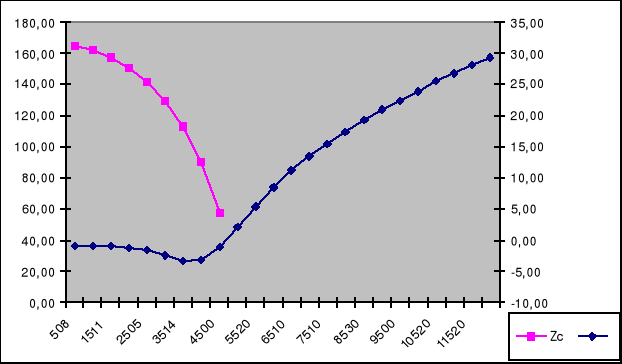
Filtr dolnoprzepustowy ma pasmo przepustowe zawarte w granicach od 0 do ω_o przy czym ω_o jest częstotliwością graniczną . W paśmie tłumienia impedancja charakterystyczna filtru dolnoprzepustowego typu “ T ” ma charakter indukcyjny. Z charakterystyki Z_c=f (f ) możemy zauważyć iż wraz ze wzrostem częstotliwości impedancja maleje do zera (przy częstotliwości granicznej). Wobec tego praca filtru w pobliżu częstotliwości granicznej ω_o nie jest korzystna.

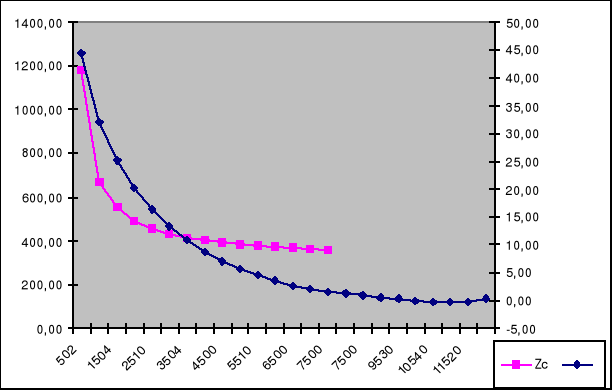
W filtrach górnoprzepustowych zakres tłumienia występuje w granicach od 0 do ω_o , współczynnik tłumienia w tym zakresie osiąga duże wartości. W paśmie tłumienia impedancja charakterystyczna filtru górnoprzepustowego typu “ Π ” ma charakter indukcyjny . Zakres przepuszczania występuje dla ω > ω_o . Z charakterystyki Z_c=f (f ) możemy zauważyć że przy wielkich częstotliwościach impedancja charakterystyczna jest bliska wartości
i zmienia się nieznacznie. W miarę zbliżania się od wielkich częstotliwości ku częstotliwości granicznej zmiany impedancji charakterystycznej są szybkie i dążą do nieskończoności. Praca filtru w pobliżu częstotliwości granicznej ω_o nie jest korzystna.

7. Wykresy:

Charakterystyka α, Zc = F(f) dla filtru dolnoprzepustowego

Charakterystyka α, Zc = F(f) dla filtru górnoprzepustowego

---