AKADEMIA GÓRNICZO – HUTNICZA

im. Stanisława Staszica w Krakowie

Wydział Inżynierii Mechanicznej i Robotyki

Modelowanie dwukołowego

robota mobilnego

Kinematyka i Dynamika Ukladów Mechatronicznych

Specjalność: Projektowanie Mechatroniczne

studia magisterskie

Wykonał:

Prusiński Wojciech

SPIS TREŚCI

1.

Wstęp .............................................................................................................. 3

2.

Kinematyka dwukołowego robota mobilnego .................................................. 3

3.

Dynamika dwukołowego robota mobilnego - Lagrange ................................. 12

4.

Dynamika dwukołowego robota mobilnego - Maggie .................................... 14

5.

Identyfikacja dwukołowego robota mobilnego .............................................. 15

1. Wstęp

Pojęcie robotów kołowych obejmuje te roboty, których podwozie umieszczone

jest na kołach. Istnieje wiele rozwiązań konstrukcyjnych tego rodzaju robotów. Spora
część z nich znalazła zastosowanie w dziedzinie nauki i techniki. Podstawowym
kryterium klasyfikacji robotów kołowych jest ilość kół napędzanych i kierowanych.
I tak na przykład dwukołowy robot mobilny posiada dwa koła napędzane, pozostałe
koła są tylko samonastawne. Przykładami takich robotów są między innymi Pioneer
2DX czy nBot.

Celem niniejszego projektu było zamodelowanie w środowisku Matlab-Simulink

kinematyki oraz dynamiki dwukołowego robota mobilnego, a następnie
przeprowadzenie jego identyfikacji. W przeprowadzonych badaniach pominięto
zupełnie wpływ koła podpierającego.

2. Kinematyka dwukołowego robota mobilnego

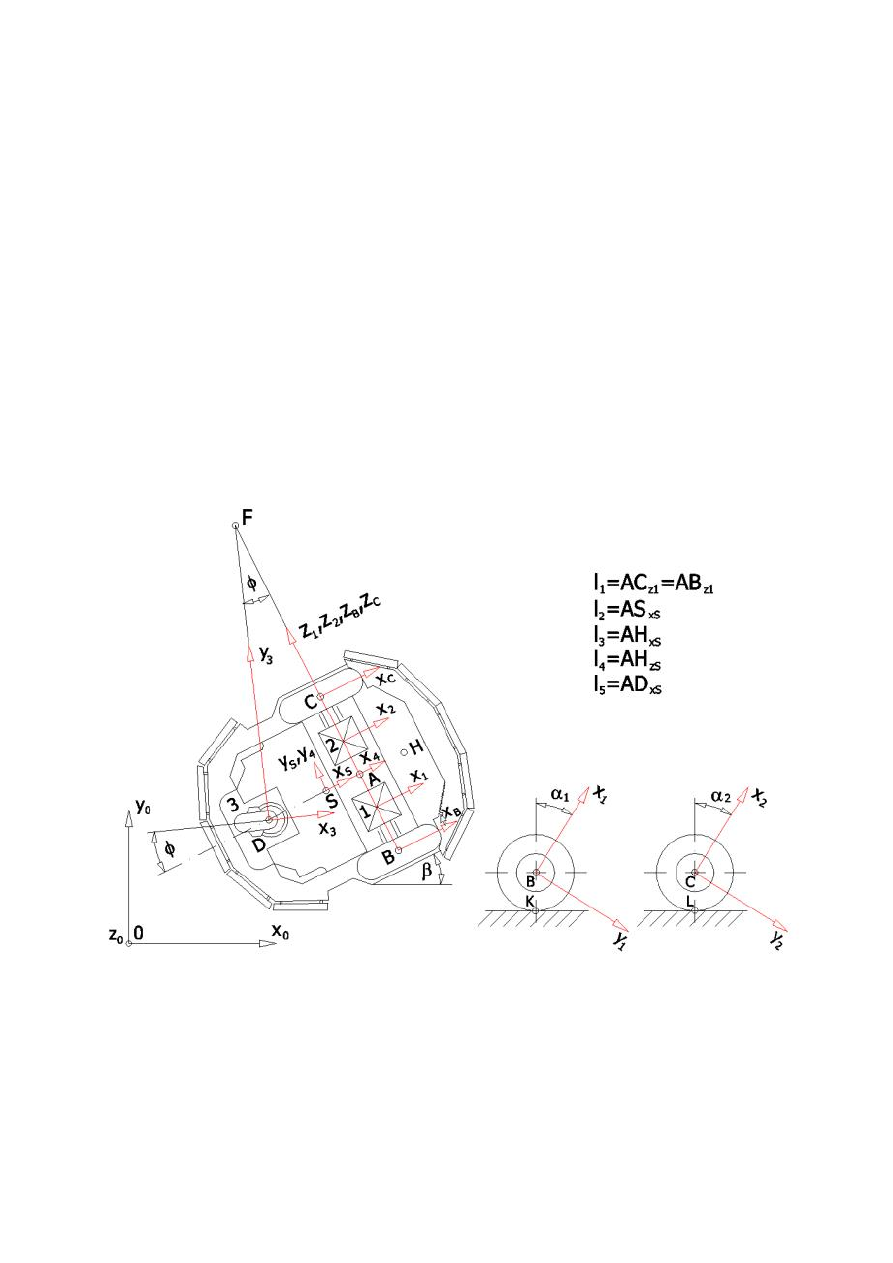
Rys. 1. Geometria modelowanego dwukołowego robota mobilnego.

Kinematyczny opis modelu opierał się na równaniach kinematycznych

wyznaczonych dla specyficznych punktów robota oraz na założeniach, że punkt A
robota poruszał się ze stałą prędkością V

A

oraz o braku poślizgu kół.

Tworząc równania kinematyczne dla charakterystycznych punktów H, A, K i L

oraz odpowiednio je przekształcając, otrzymano układ 6 równań opisujących
w sposób dostatecznych ruch dwukołowego robota mobilnego.

Równania (1) oraz (2) dotyczyły punktu H, (3) i (4) – punktu A, (5) – K i (6) – L.
Przyjęte oznaczenia, których nie uwzględniono na rys. 1.:

A

– rzut prędkości na oś x,

A

– rzut prędkości na oś y,

R – promień łuku przy skręcaniu robota,
r

1

– promień koła 1,

r

2

– promień koła 2.

Na podstawie powyższych równań przeprowadzono symulację zadania

odwrotnego kinematyki dla założonej ścieżki (rys. 2.).

Rys. 2. Założona ścieżka.

Założono również następujące parametry pracy i fizyczne cechy robota:



prędkość punktu A: V

A

= 0.6 m/s,



czas rozruchu: 2 s,



czas ruchu po prostej: 5 s,



czas ruchu po łuku: 4 s z R = 4.8/π = 1.53 m,



czas ruchu po prostej: 5 s,



czas zatrzymania: 2 s.

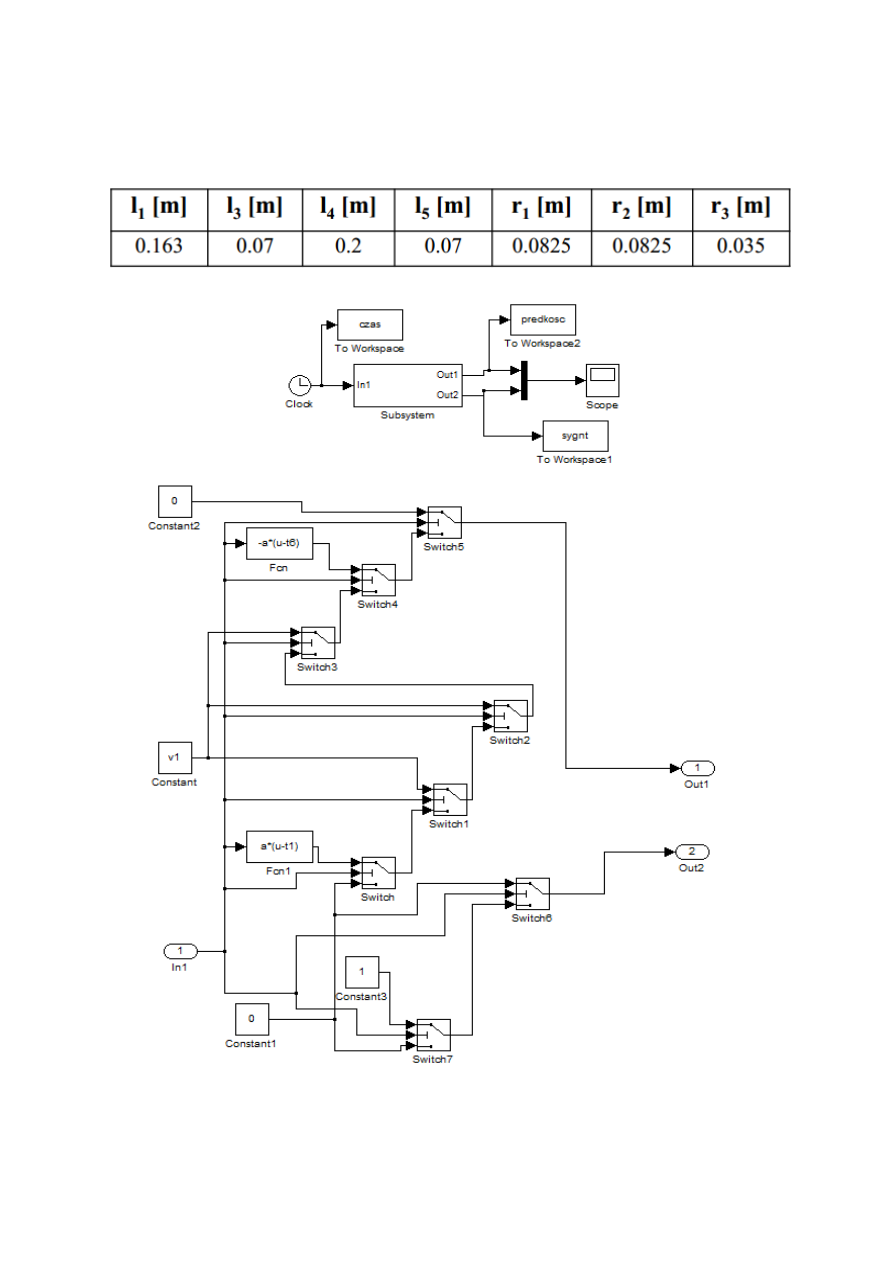
Rys. 3. Model generatora prędkości i ścieżki – subsystem (u góry) oraz wnętrze

subsystemu (na dole).

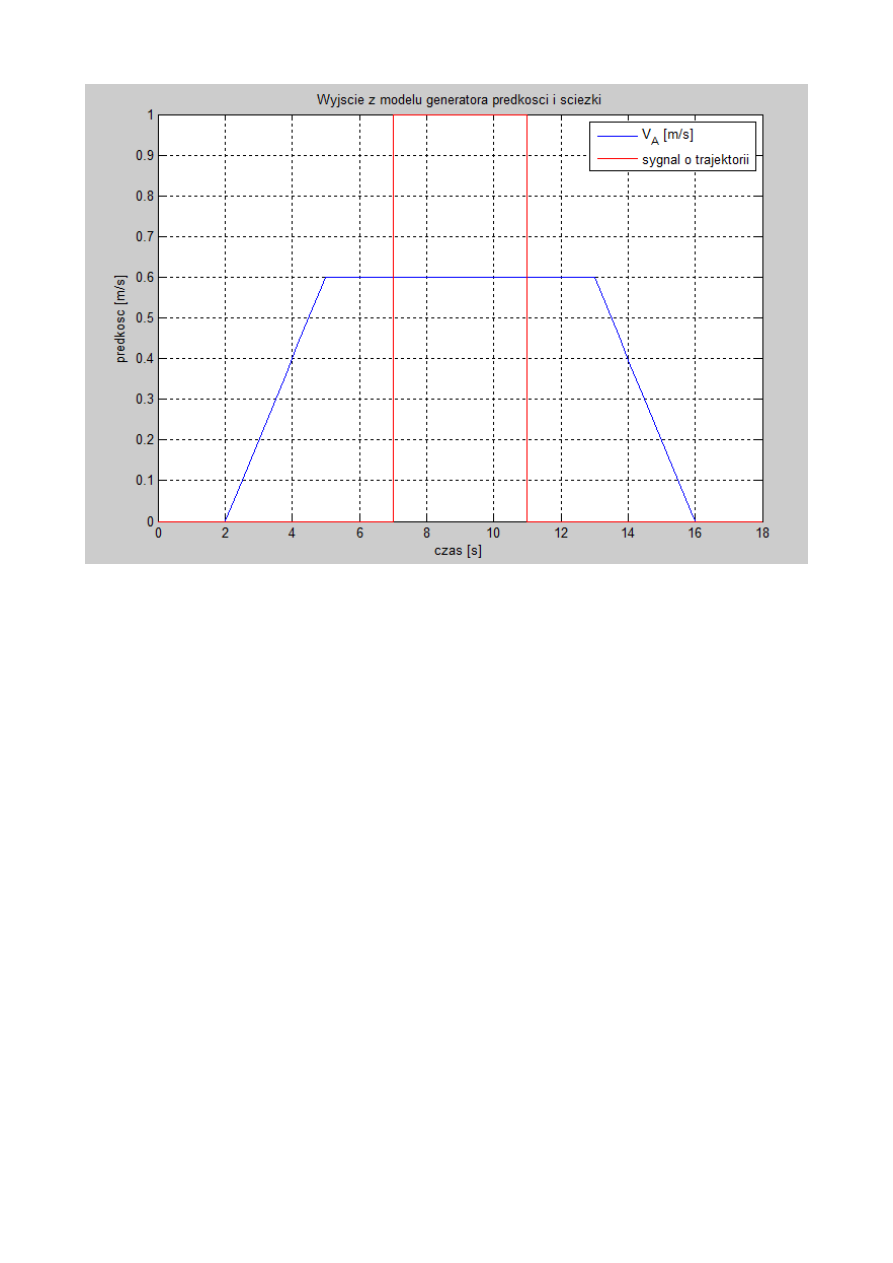
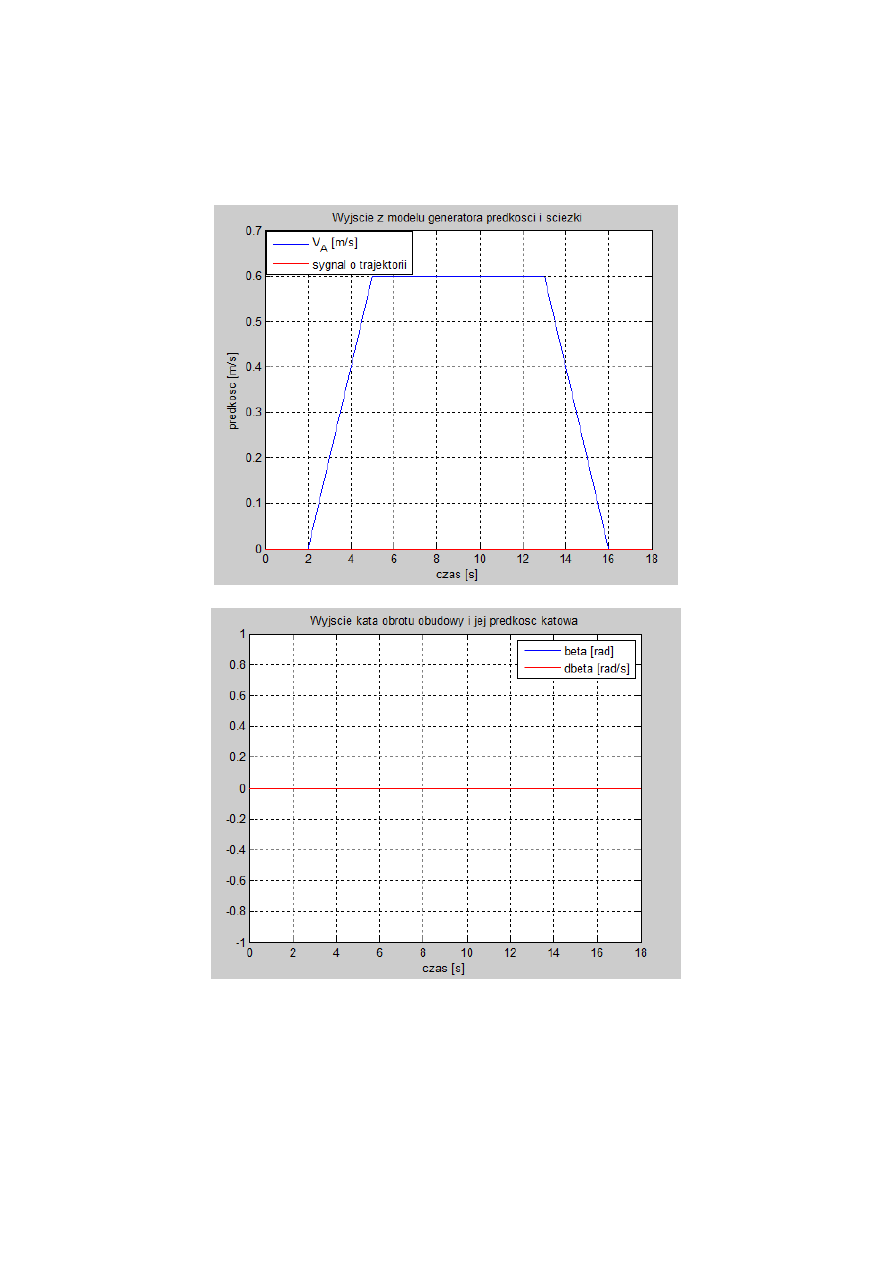
Rys. 4. Wyjście z modelu generatora prędkości i ścieżki.

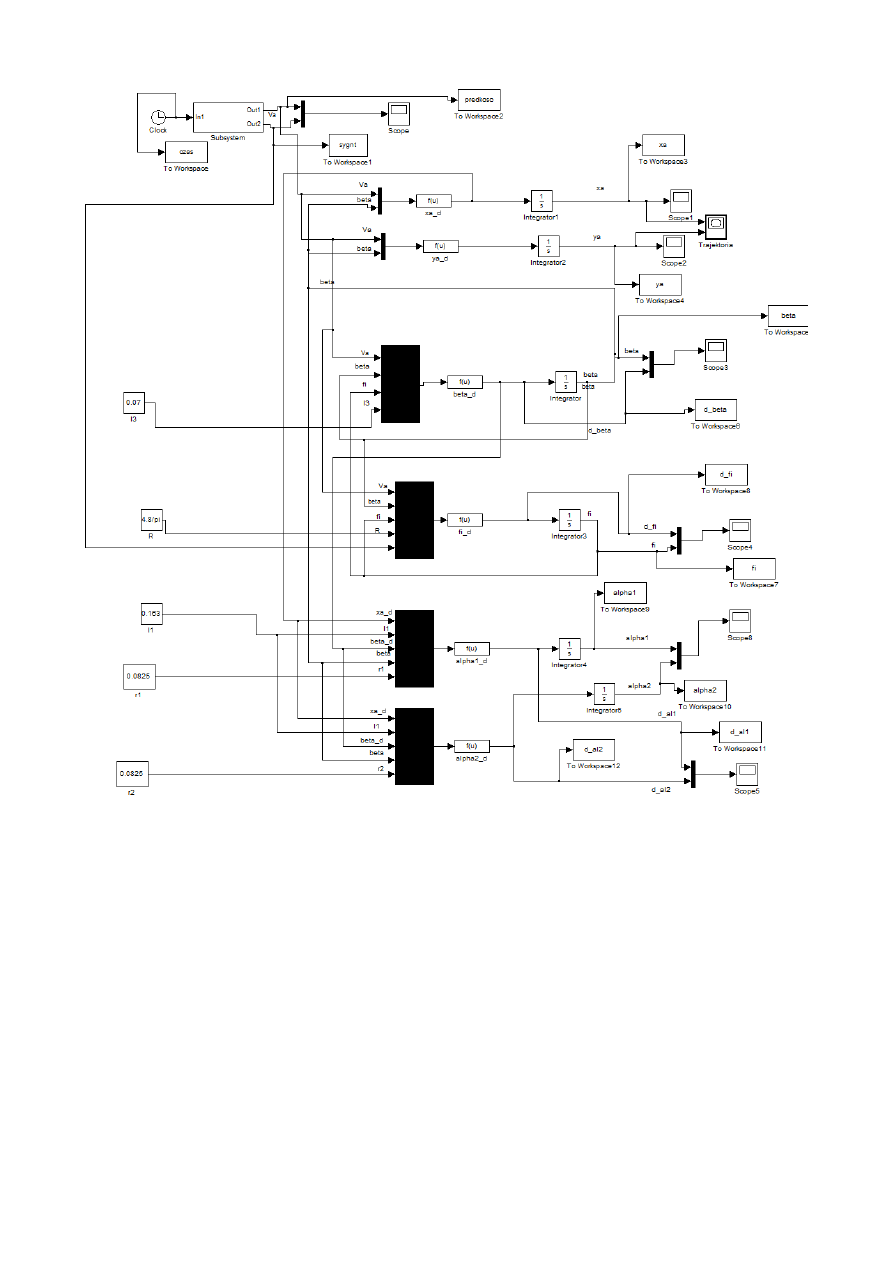
Rys. 5. Model rozwiązujący zadanie proste i zadanie odwrotne kinematyki stworzony w środowisku

Matlab-Simulink.

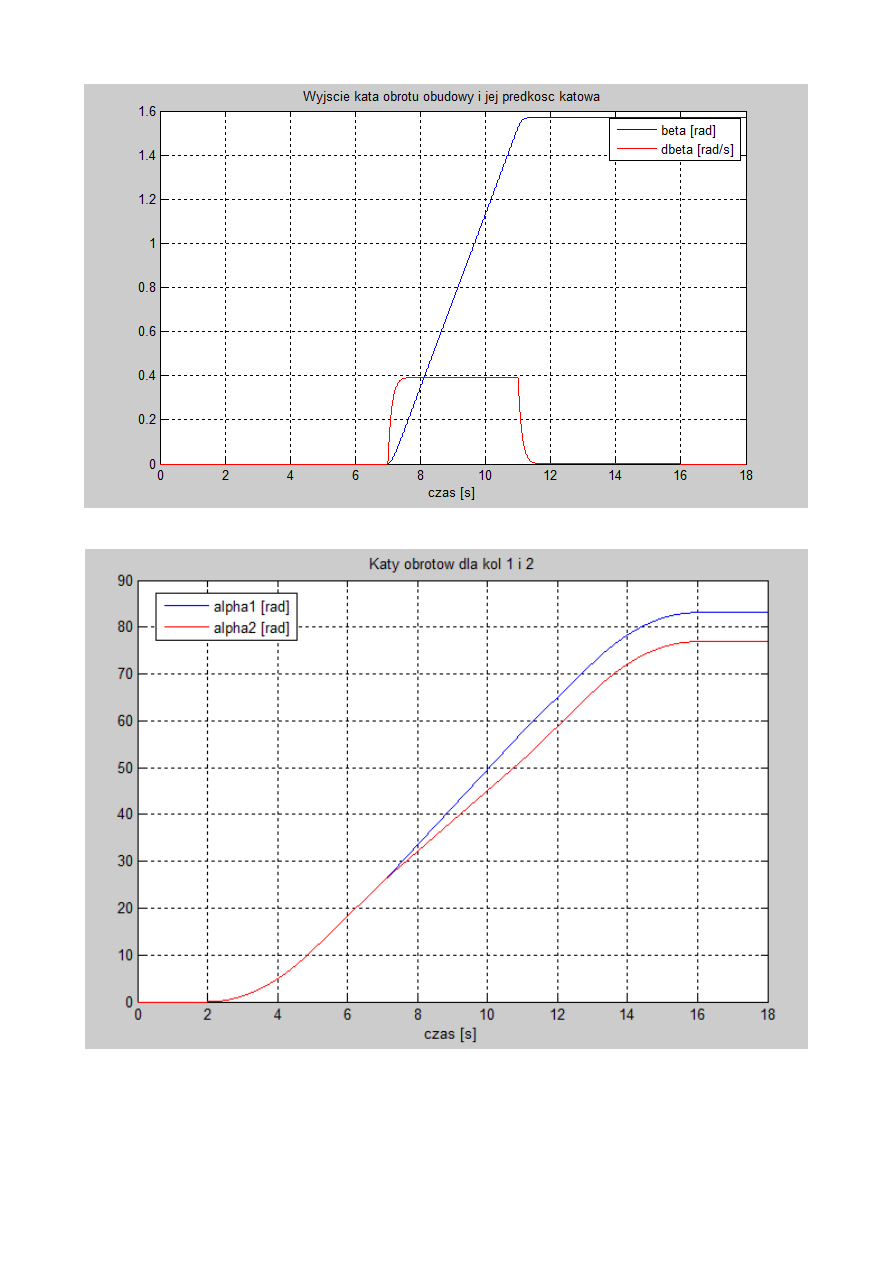
Rys. 6. Wyjście kąta obrotu obudowy i jej prędkość kątowa.

Rys. 7. Kąty obrotów dla kół 1 oraz 2.

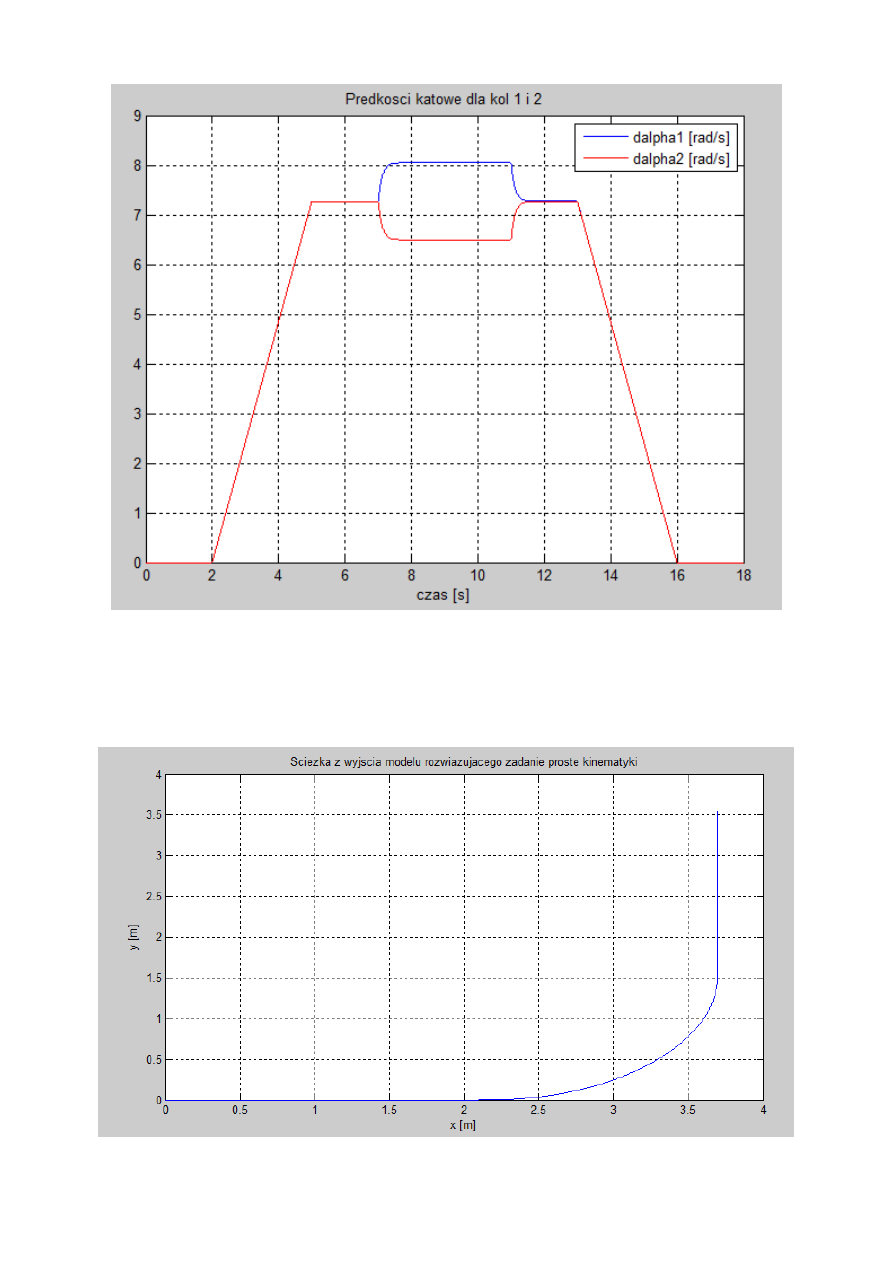
Rys. 8. Prędkości kątowe dla kół 1 oraz 2.

Dla otrzymanych wyników z rozwiązania zadania odwrotnego kinematyki,
sprawdzono poprawność tychże wyników poprzez symulację zadania prostego
kinematyki.

Rys. 9. Ścieżka otrzymana z wyjścia modelu rozwiązującego zadanie proste kinematyki.

Wynikiem jest poprzednio założona ścieżka, dlatego można wywnioskować, iż
otrzymane wyniki są prawidłowe, a model stworzono w sposób poprawny.

Zakładając inną ścieżkę (tylko linia prosta), otrzymano następujące wyniki:

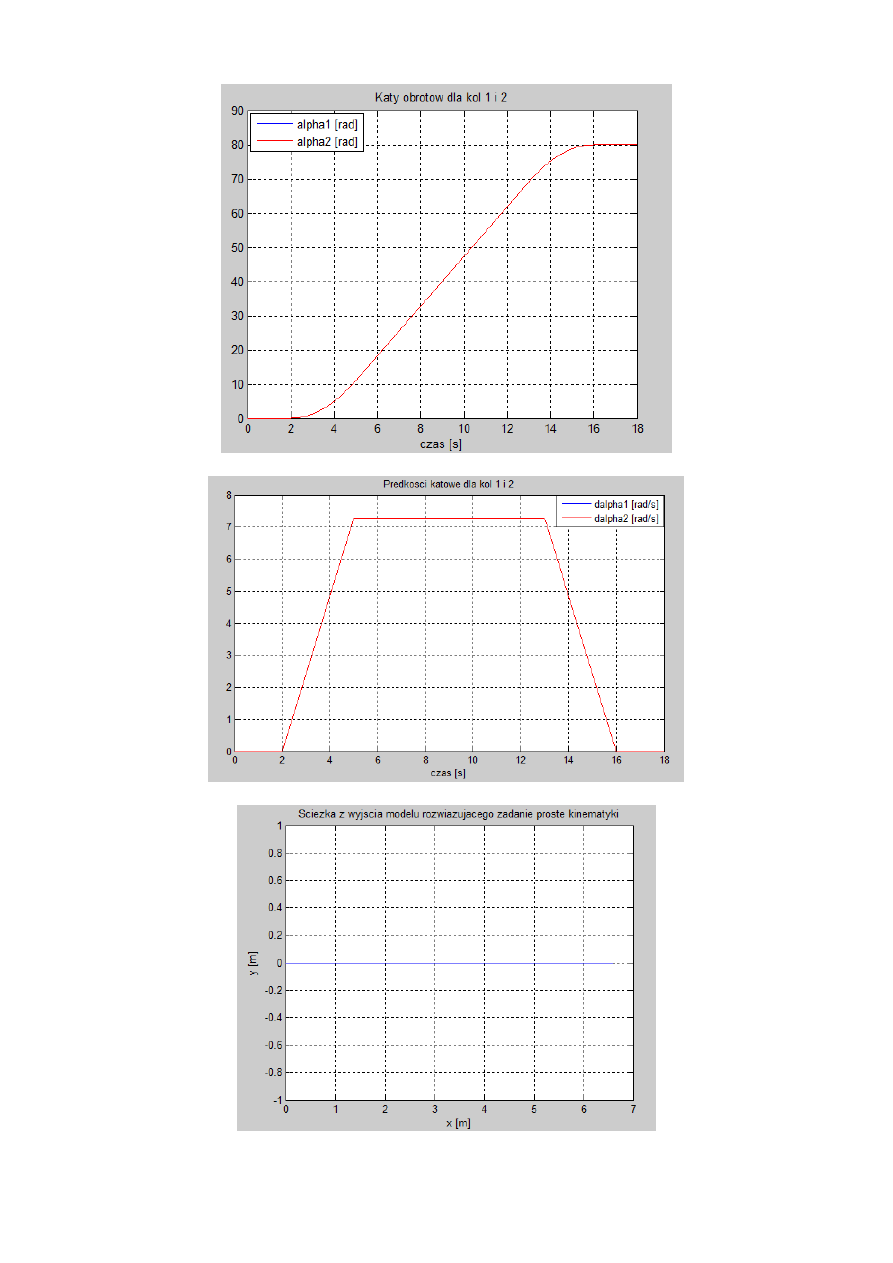
Rys. 10. Wyniki otrzymane dla ścieżki w postaci wyłącznie linii prostej.

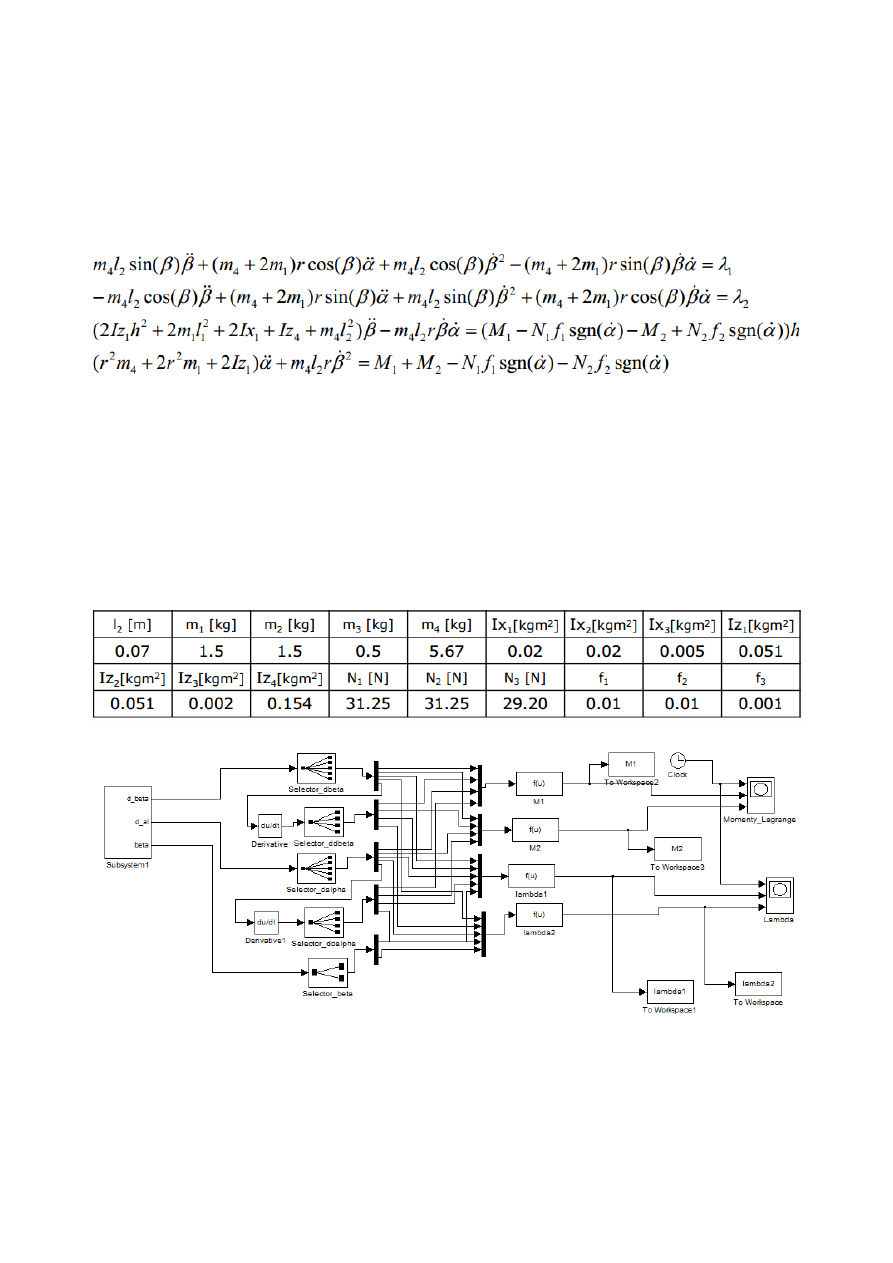
3. Dynamika dwukołowego robota mobilnego - Lagrange

Do modelowania dynamiki robotów mobilnych bardzo często wykorzystywane

są równania Lagrange’a II typu z mnożnikami (λ). Aby ich zastosowanie było w
ogóle możliwe konieczne jest zastosowanie transformacji odsprzęgającej mnożniki
od momentów napędzających. W przypadku badanego obiektu miały one postać:

Z dwóch pierwszych równań wyznaczono mnożniki Lagrange’a (bez konieczności
jakichkolwiek przekształceń). Natomiast z dwóch ostatnich równań (z których
wyznaczono momenty napędzające M1 oraz M2) stworzono prosty układ – 2
równania, 2 niewiadome.

Dla ścieżki z poprzedniego rozdziału (pierwszy przypadek – z łukiem) oraz cech
fizycznych robota podanych w poniższej tabeli stworzono model symulacji dynamiki.

Rys. 11. Model symulacji dynamiki dwukołowego robota mobilnego.

Po zbudowaniu modelu w środowisku Matlab-Simulink, wykreślono zależności M1,
M2 – czas oraz lambda1, lambda2 – czas.

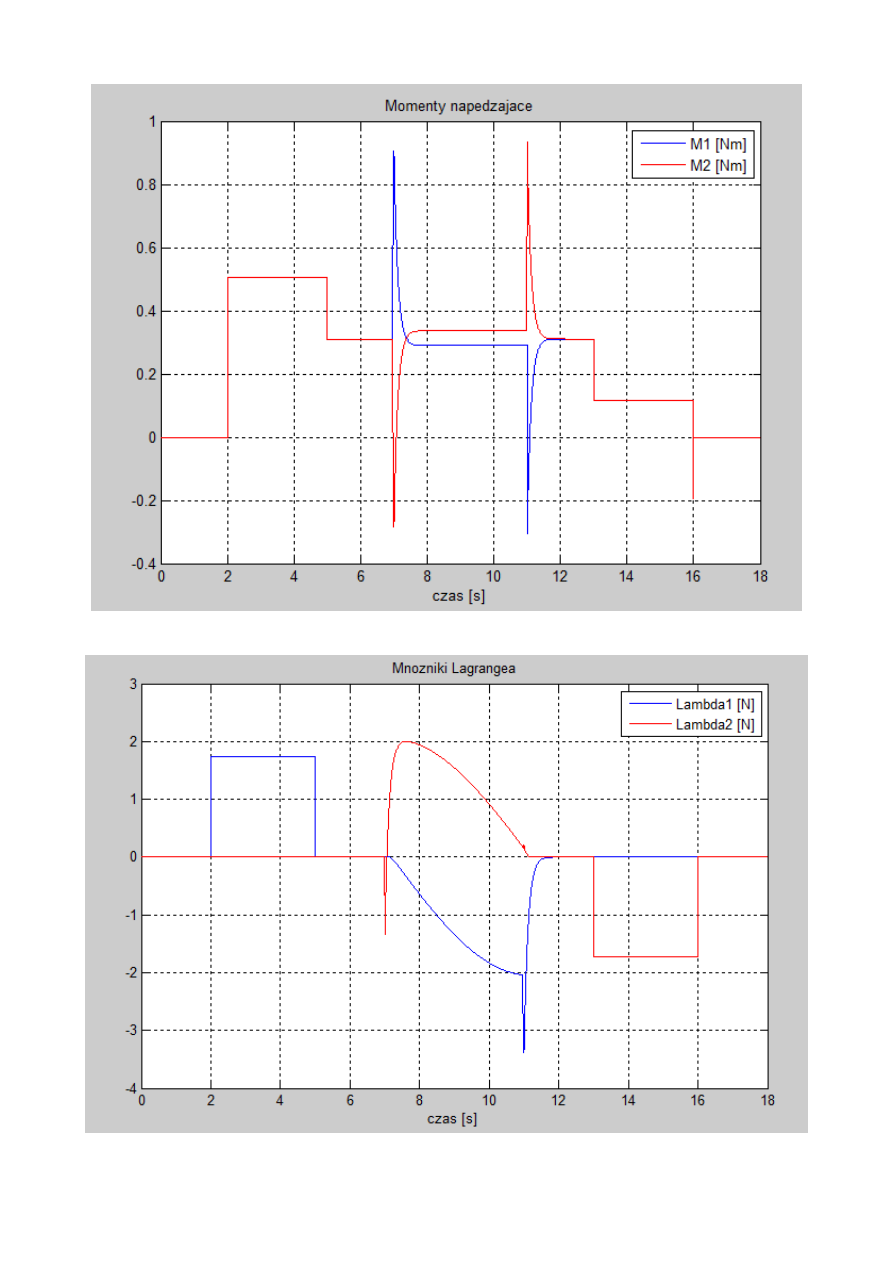
Rys. 12. Momenty napędzające M1, M2 w zależności od czasu.

Rys. 13. Mnożniki Lagrange’a Lambda1 oraz Lambda2 w zależności od czasu.

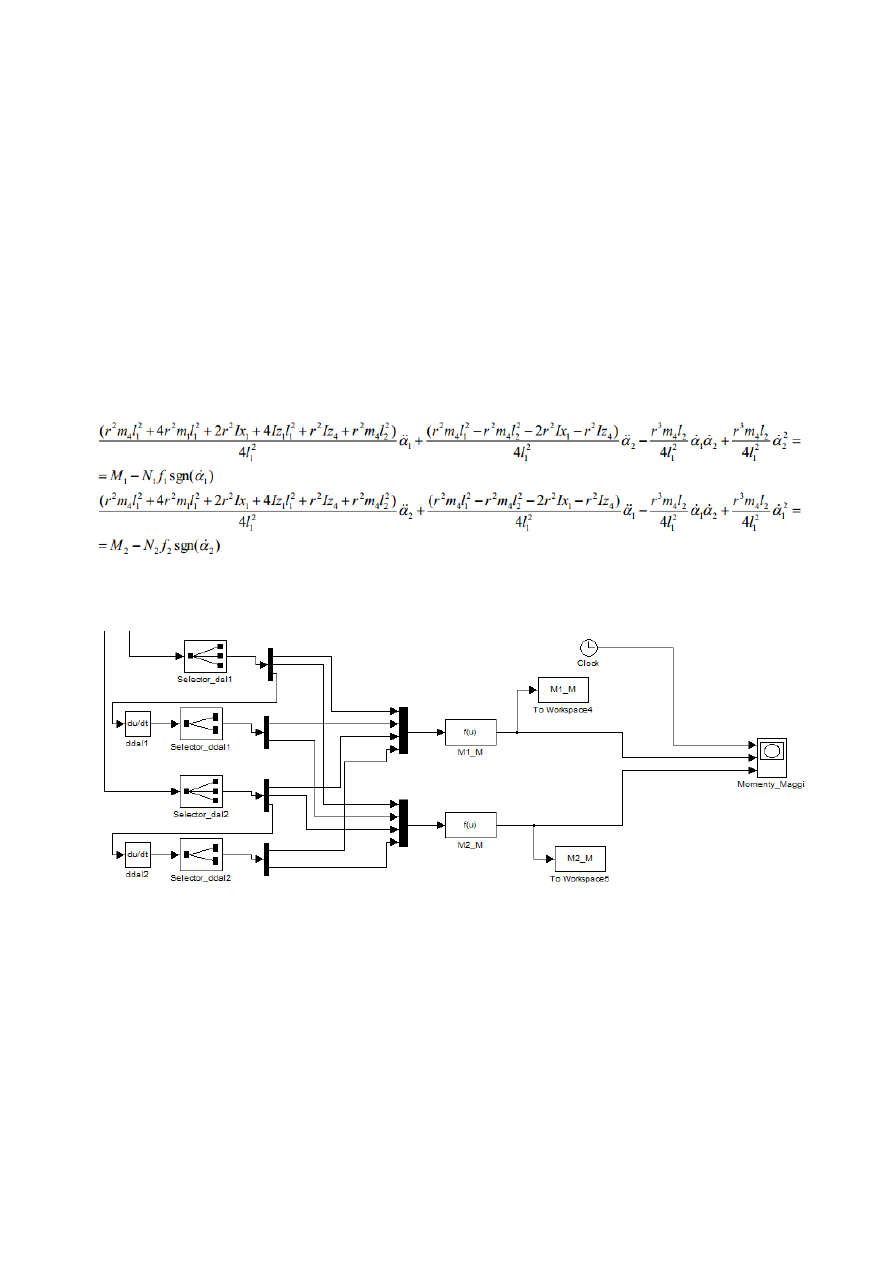
Gwałtowne skoki wartości (piki) na wykresach momentów napędzających oraz
mnożników nie są rzeczywistymi zmianami w układzie, a jedynie efektem
zastosowania nieróżniczkowalnej funkcji w generatorze prędkości V

A

(rys. 4.).

4. Dynamika dwukołowego robota mobilnego - Maggie

Oprócz równań i mnożników Lagrange’a, do modelowania dynamiki robotów

bardzo często stosuje się równania Maggie’go, które bazują na równaniach
Lagrange’a. Ich główną zaletą jest brak konieczności stosowania transformacji
odsprzęgającej.

Dla badanego obiektu, równania te przyjęły postać:

Z pierwszego równania wyznaczono moment napędzający M1, a z drugiego – M2.

Rys. 14. Model umożliwiający symulację problemu odwrotnego dynamiki dla równań Maggie’go

(wejściami do modelu są sygnały prędkości kątowych dla kół 1 i 2).

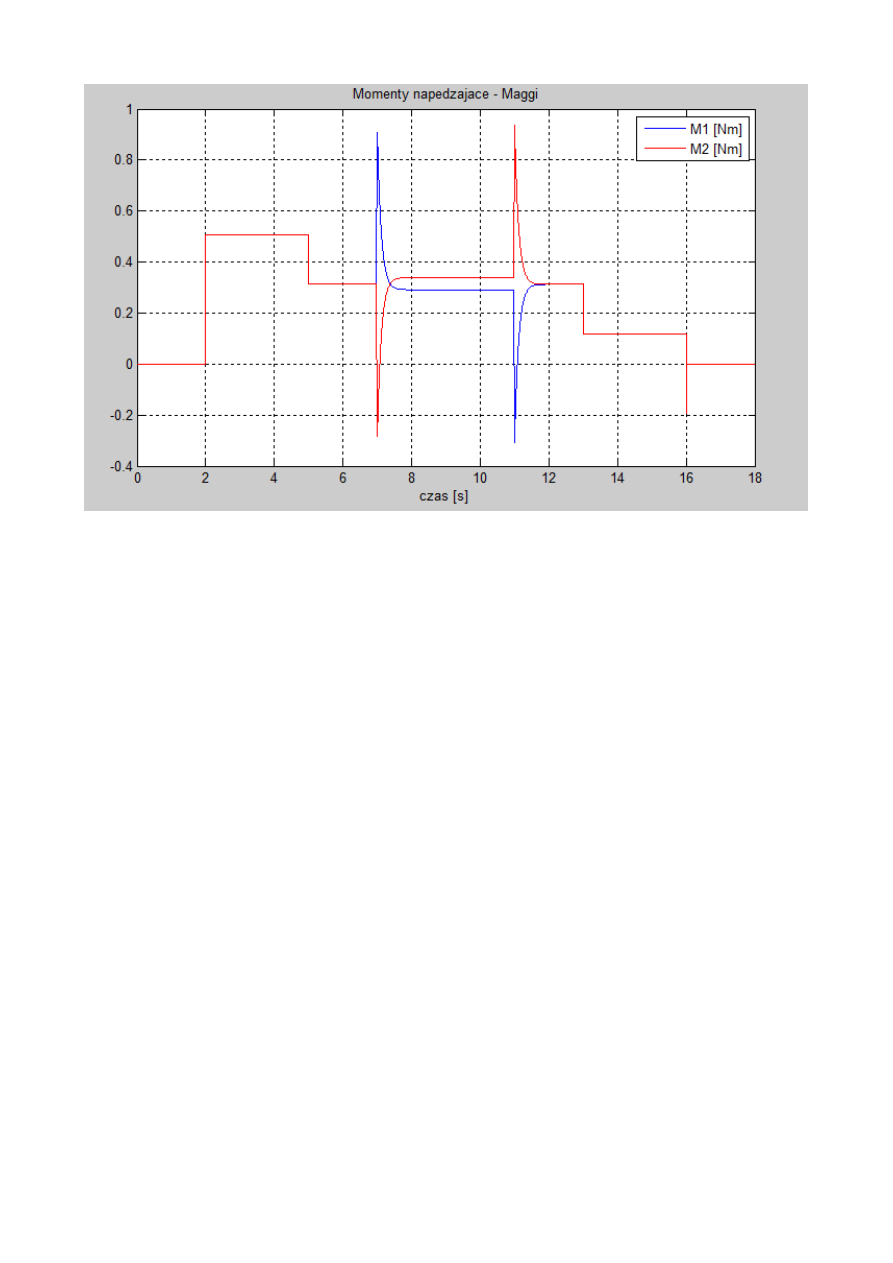
Rys. 15. Momenty napędzające M1, M2 w zależności od czasu otrzymane z równań Maggie’go.

Gwałtowne skoki wartości (piki) na wykresie momentów napędzających nie są
rzeczywistymi zmianami w układzie, a jedynie efektem zastosowania
nieróżniczkowalnej funkcji w generatorze prędkości V

A

(rys. 4.).

5. Identyfikacja dwukołowego robota mobilnego

Zagadnienie identyfikacji dotyczy oceny modelu w pewnej klasie modeli

sformułowanych na podstawie opisu zjawisk fizycznych (przy użyciu aparatu
matematycznego) zachodzących w rzeczywistym analizowanym obiekcie.

Metodą rozwiązania zagadnienia identyfikacji wykorzystaną w niniejszym

projekcie jest logika rozmyta (fuzzy logic). Zastosowano również równoległą
strukturę identyfikacji parametrów.

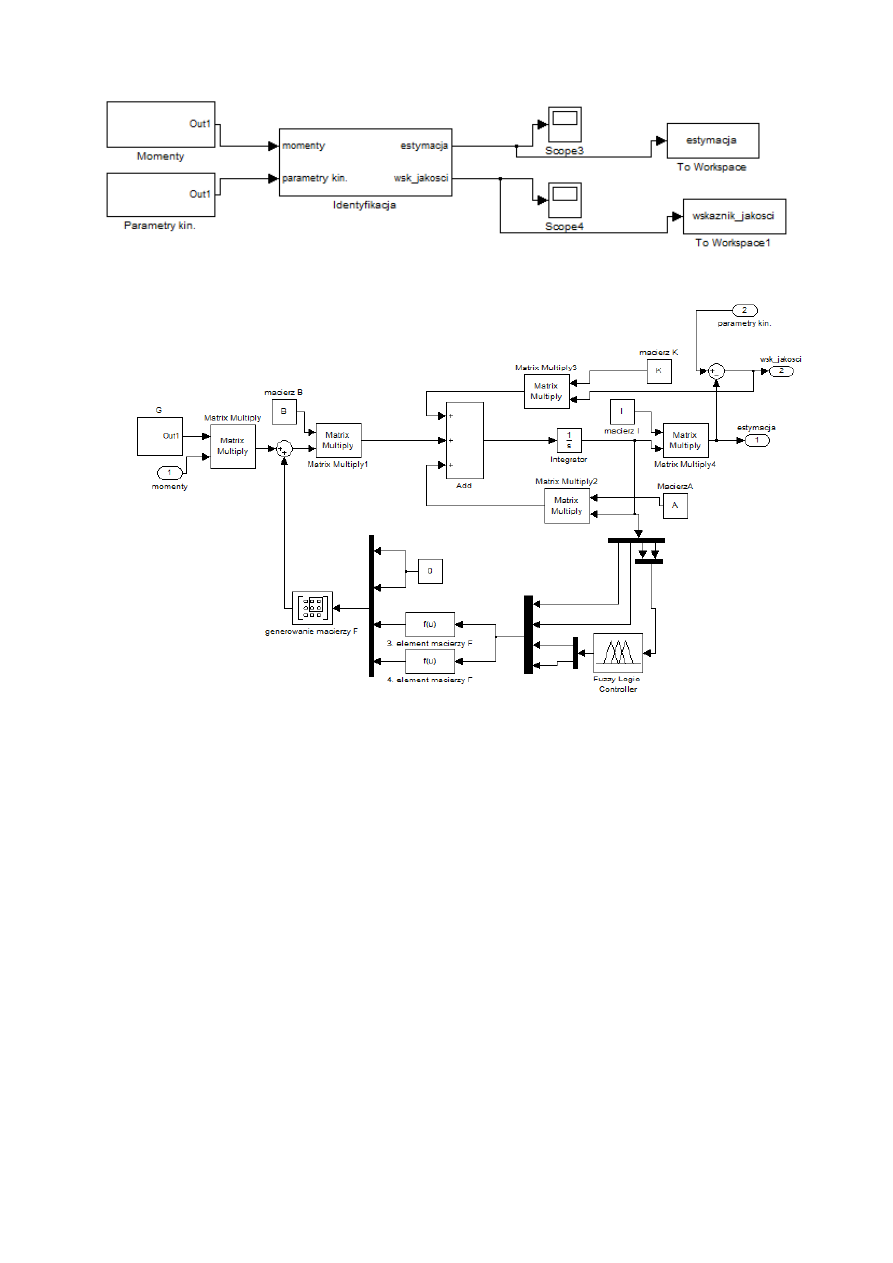
Rys. 16. Równoległa struktura emulatora stanu – subsystem (u góry) i jego wnętrze (na dole).

Po zbudowaniu modelu emulatora w środowisku Matlab-Simulink przeprowadzono
eksperyment, którego wynikiem było wyplotowanie wykresów (rys. 17, 18, 19, 20 i
21).

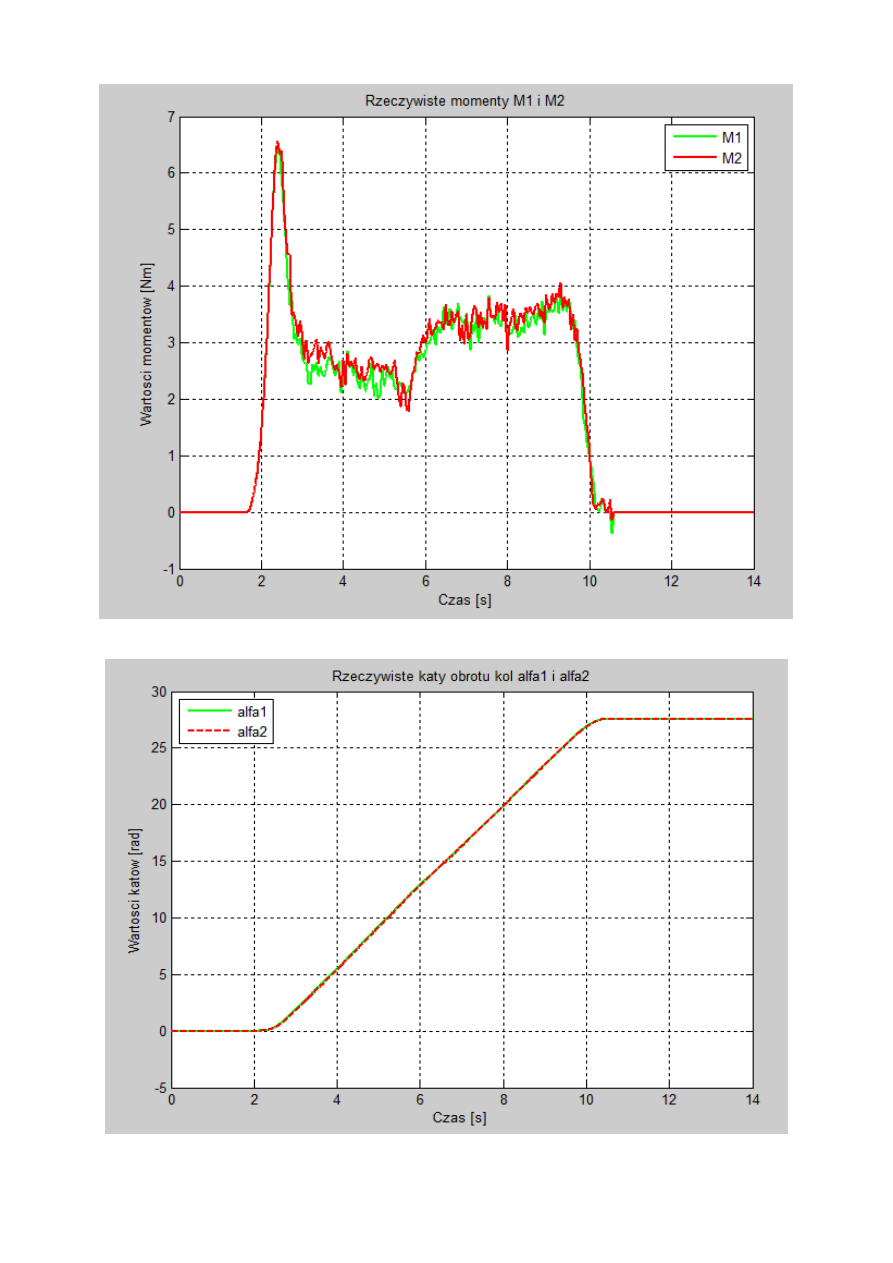
Rys. 17. Rzeczywiste momenty napędzające M1, M2 w zależności od czasu.

Rys. 18. Rzeczywiste kąty obrotu kół – alfa1 i alfa2 w zależności od czasu.

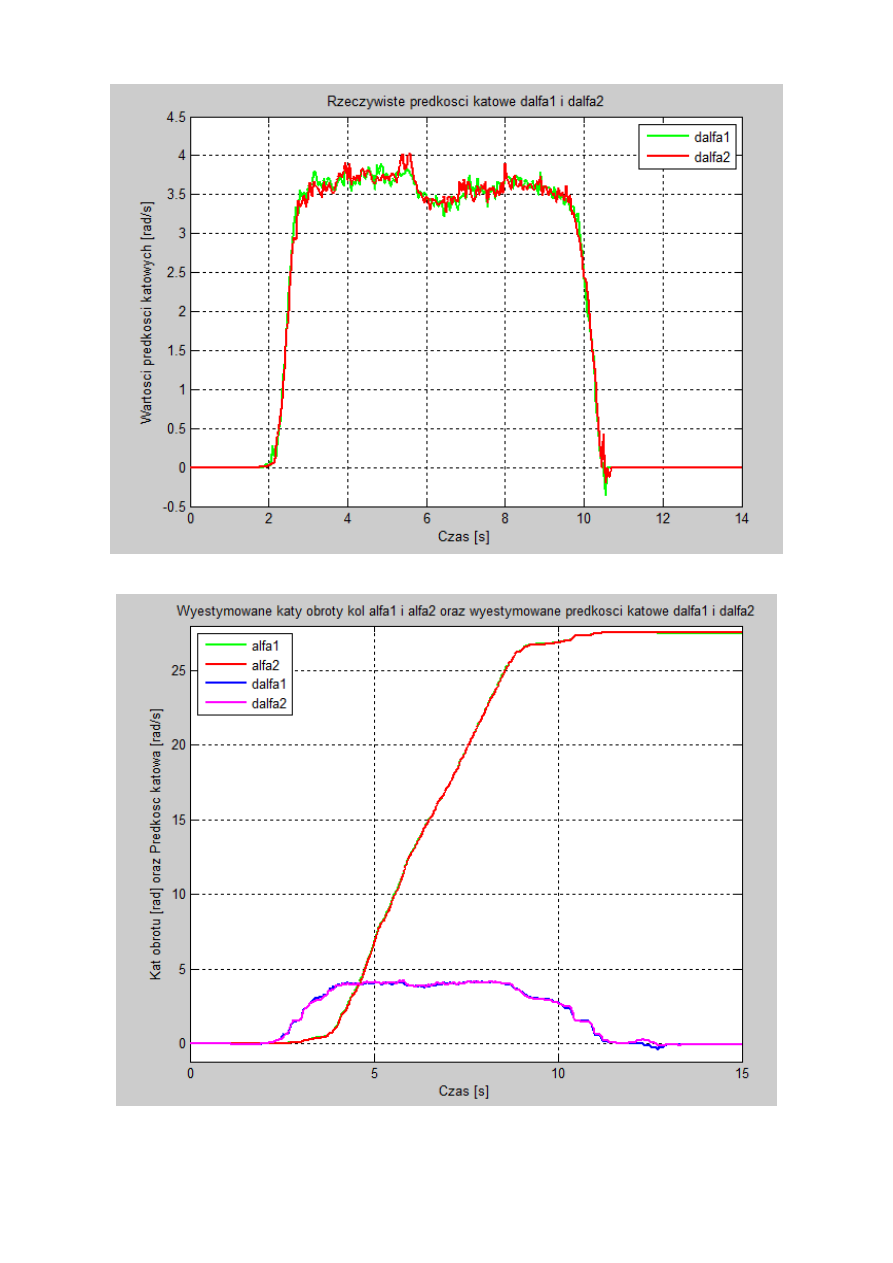
Rys. 19. Rzeczywiste prędkości obrotowe kół – dalfa1 i dalfa2 w zależności od czasu.

Rys. 20. Wyestymowane wartości kątów obrotów kół – alfa1 i alfa2 oraz prędkości kątowych –

dalfa1 i dalfa2.

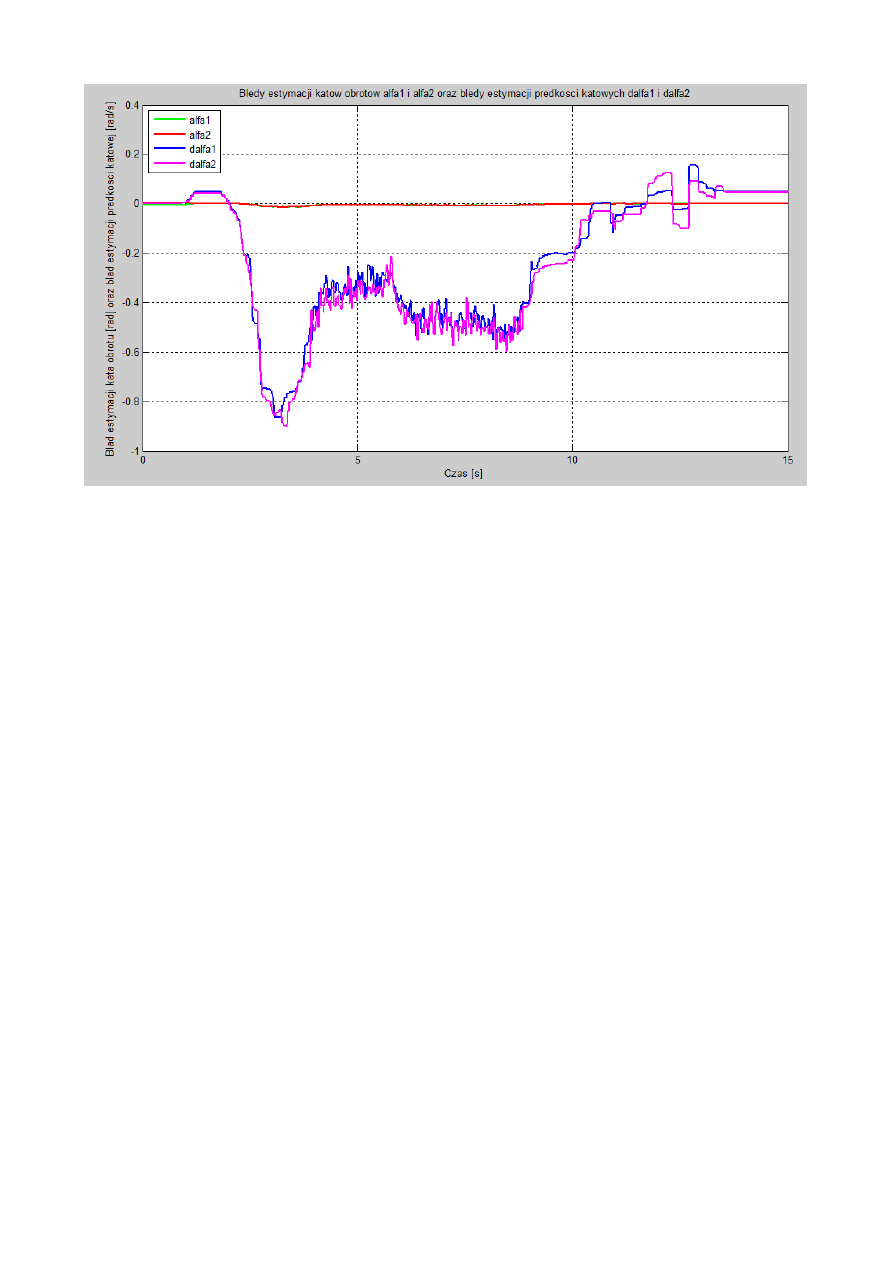
Rys. 21. Błędy estymacji wartości kątów obrotów kół – alfa1 i alfa2 oraz prędkości kątowych –

dalfa1 i dalfa2.

Do sprawozdania dołączono pliki dotyczące wszystkich etapów niniejszego projektu.