Ćwiczenie 29
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH
ZA POMOCĄ ŁAWY OPTYCZNEJ
29.1. Opis teoretyczny
Soczewką sferyczną nazywamy przezroczystą bryłę ograniczoną dwoma powierzchniami sferycz-
nymi o promieniach R
1
i R
2
. Prostą która przechodzi przez środki krzywizn obu powierzchni nazy-
wamy osią główną. Soczewki ze szkła w środku grubsze – są zbierające, soczewki cieńsze w środku
niż na brzegach – są rozpraszające. Wiązka promieni równoległych do osi głównej po załamaniu w
soczewce zbierającej zostaje zebrana w ognisku F, którego odległość od środka optycznego so-
czewki nazywamy odległością ogniskową f. Środek optyczny soczewki ma tę właściwość, że
wszystkie promienie padające na soczewkę, a skierowane na ten punkt, nie zmieniają kierunku, lecz
ulegają minimalnemu przesunięciu równoległemu. W przypadku soczewek cienkich, które są
przedmiotem naszych rozważań, środek geometryczny soczewki pokrywa się ze środkiem optycz-
nym.
Zależność odległości f od promieni krzywizn oraz współczynnika załamania światła ośrodka, z któ-
rego wykonana jest soczewka względem ośrodka otaczającego soczewkę n, określona jest równa-
niem:
+
−
=
2
1
R
1
R
1
1)
(n
f
1
(29.1)
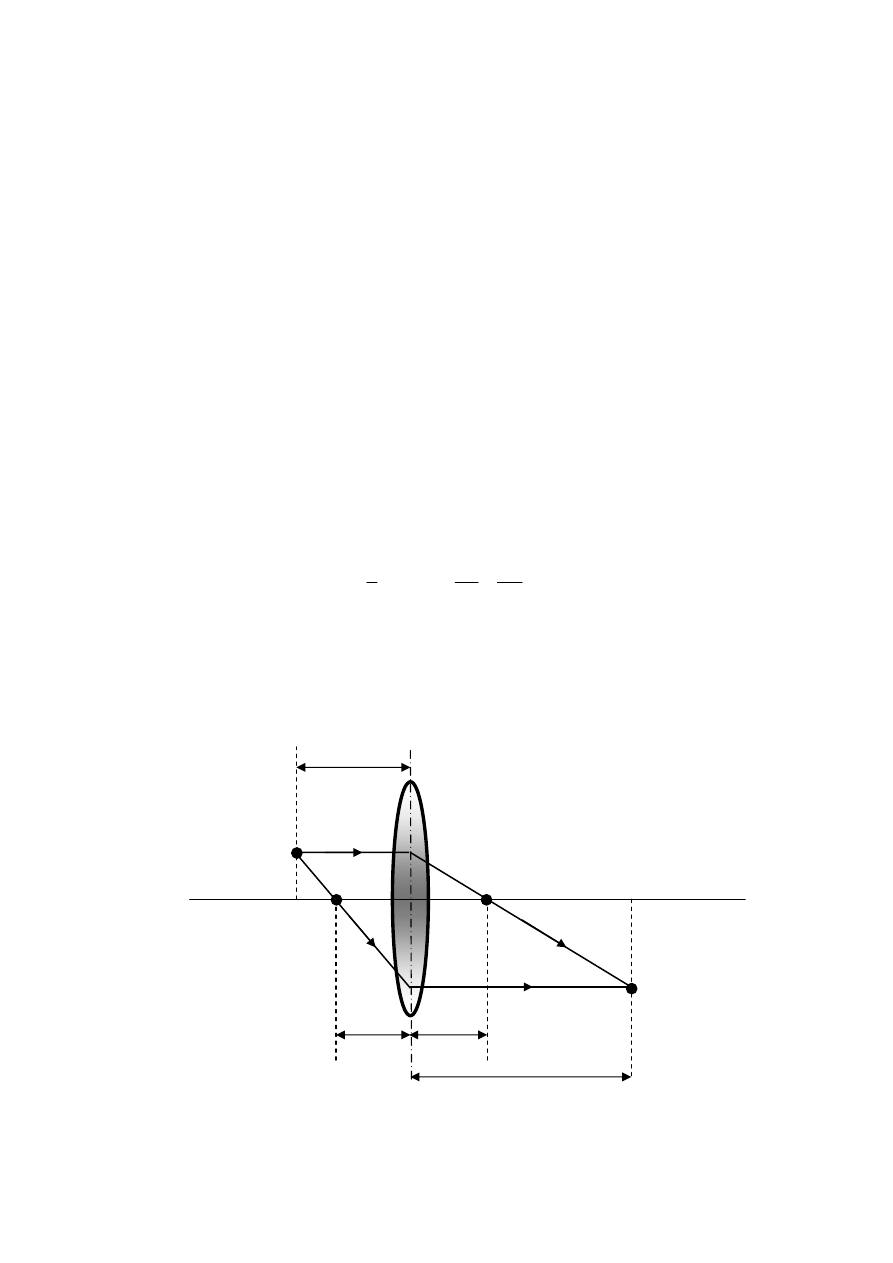
Promienie wychodzące z dowolnego punktu A (rys. 29.1) wskutek ich załamania w soczewce, zo-
stają zebrane w innym punkcie B, który jest obrazem punktu A. Jeśli przedmiot składa się z wielu
punktów wysyłających światło, to każdemu z nich można przyporządkować odpowiedni punkt ob-
razu.
a
A
F
F
Oś główna
B
f
f
b
Rys. 29.1. Obraz rzeczywisty punktu świecącego wytwarzany przez soczewkę.

Obrazy wytwarzane w soczewkach mogą być rzeczywiste lub pozorne. Cechą tych ostatnich jest to,
że nie można ich uzyskać na ekranie lub kliszy, a ich powstawanie związane jest z właściwością
oka ludzkiego.
Obraz nazywamy rzeczywistym, gdy promienie załamane zbierają się w punkcie B lub urojonym,
gdy zbierają się tam przedłużenia promieni (rys. 29.2). Gdy w miejscu obrazu rzeczywistego umie-
ścimy ekran, wówczas ujrzymy na nim obraz B. Obrazu urojonego na ekranie otrzymać nie można.
Obrazy rzeczywiste leżą zawsze po stronie przeciwnej względem soczewki, zaś obrazy pozorne po
tej samej co przedmiot. Umieszczeniu przedmiotu w pewnej odległości od soczewki towarzyszy
więc powstanie jego obrazu w ściśle określonym miejscu. Z prostych zależności geometrycznych
można otrzymać dla cienkiej soczewki związek między położeniem przedmiotu a położeniem wy-
tworzonego jego obrazu:
b
1
a
1
f
1
+
=
(29.2)
gdzie: a - odległość przedmiotu od soczewki, b - odległość obrazu od soczewki.
Powyższe równanie nosi nazwę równania soczewki cienkiej i stanowi bardzo ważną właściwość
wykorzystywaną w ćwiczeniu. Opisuje ono wszystkie możliwe przypadki położeń przedmiotów i
utworzonych obrazów, np. dla promieni światła równoległych do osi optycznej soczewki a =
∞
= 0
a
1
obliczamy b = f, a więc promienie te po przejściu przez soczewkę utworzą obraz w jej
ognisku. Jest to zgodne z definicją ogniska.
Gdy przedmiot zbliża się do soczewki z nieskończoności, „a” zmniejsza się, ponieważ prawa strona
równania (29.2) pozostaje niezmieniona, wobec tego „b” musi rosnąć. Obraz oddala się od soczew-
ki, tak więc zarówno przedmiot jak i jego obraz poruszają się w tę samą stronę. Dla a = 2f mamy b
= 2f, co oznacza, że odległości przedmiotu i obrazu od soczewki są wówczas jednakowe. Gdy
przedmiot przesuwa się od 2f do f, wtedy obraz odsuwa się od soczewki, gdy zaś a = f oddala się on
do nieskończoności. Możemy powiedzieć, że promienie wychodzące z ogniska po przejściu przez
soczewkę skupiającą biegną jako wiązka równoległa do osi głównej.
W geometrycznej konstrukcji obrazów posługujemy się promieniami, których bieg po załamaniu w
soczewce spełnia następujące warunki:
1. promień wychodzący z ogniska po załamaniu w soczewce biegnie równolegle do jej osi
głównej,
2. promień równoległy do osi po załamaniu przechodzi przez ognisko,
3. promień przechodzący przez środek optyczny soczewki nie doznaje zmiany kierunku.
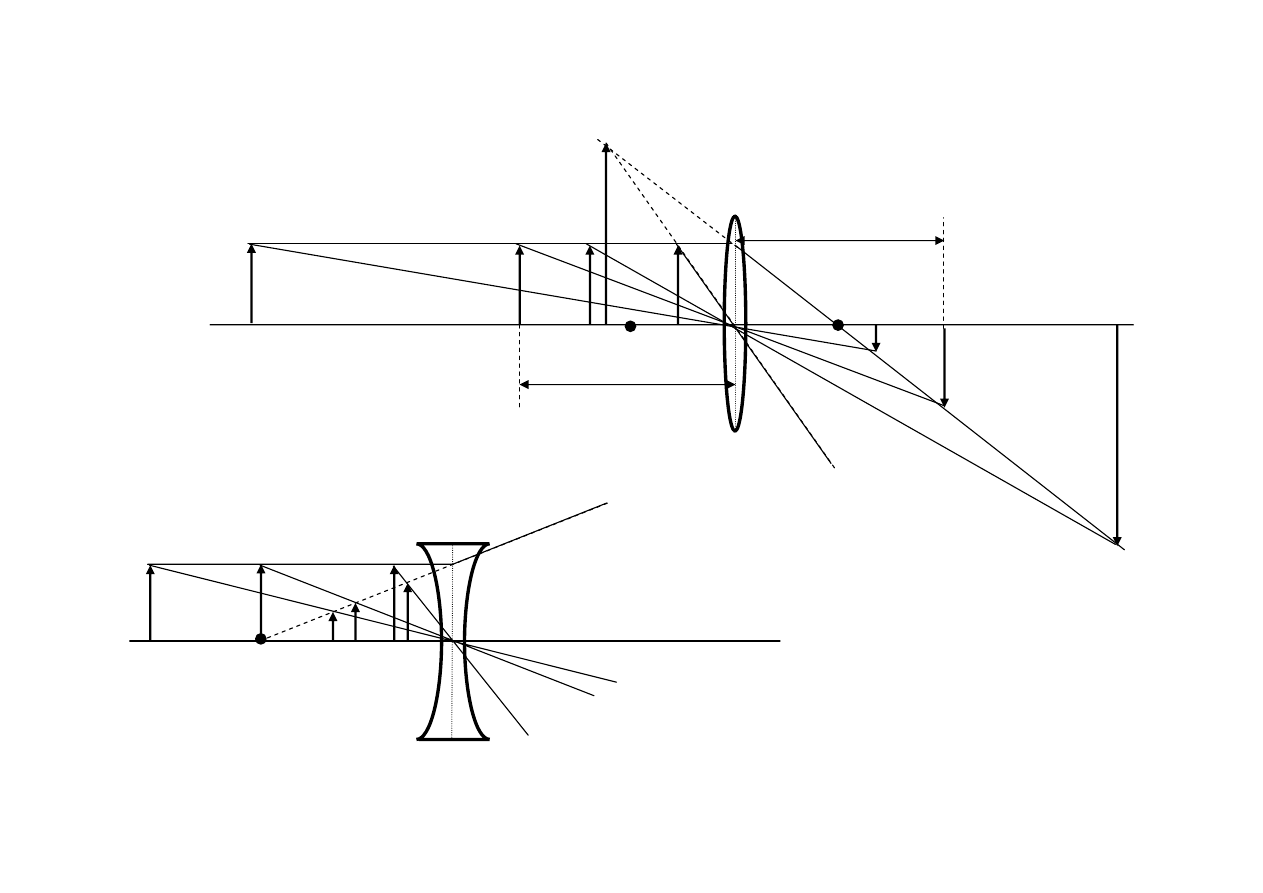
Obrazy powstające w różnych odległościach od soczewki mają różne wielkości w stosunku do
wielkości przedmiotu. Ilustruje to rys. 29.2a,b Pozycje przedmiotu oznaczono cyframi 1,2,3,4,5,6,7,
a odpowiadające im pozycje obrazów cyframi primowanymi 1’, 2’, 3’, 4’, 5’, 6’, 7’. Obrazy 4’, 5’,
6’, 7’, są pozorne (b < 0). Z konstrukcji geometrycznych zrobionych dla soczewki rozpraszającej
(rys. 29.2b) widzimy, że tworzy ona jedynie obrazy pozorne, proste i pomniejszone.
a)
4’
1
2
3
4
2f
F
2
F
1
1’
2f
2’
b)
5
6
7
7’
6’
3’
5’
F
1
Rys. 29.2. Konstrukcja obrazów wytworzonych przez soczewkę: a) skupiającą, b) rozpraszającą.

T a b e l a 29.1
Obrazy w soczewkach sferycznych
Lp.
Odległość przedmiotu
Odległość obrazu
Obraz
Soczewki skupiające ( f > 0 )
1
2
3
4
a > 2f
a = 2f
f < a < 2f
a < f
f < b < 2f
b = 2f
b > 2f
b < 0
rzeczywisty, odwrócony, zmniejszony
rzeczywisty, odwrócony, równy przed-
miotowi
rzeczywisty, odwrócony, powiększony
urojony, prosty, powiększony
1’
2’
3’
4’
Soczewki rozpraszające ( f < 0 )
5
6
7
a > f
a = f
a < f
b < 0
b < 0
b < 0
urojony, prosty, pomniejszony
urojony, prosty, pomniejszony
urojony, prosty, pomniejszony
5’
6’
7’
Odległość ogniskowa f jest wielkością charakteryzującą załamanie promieni w soczewce; im zała-
manie jest silniejsze, tym odległość ogniskowa jest krótsza i odwrotnie. W praktyce załamanie
promieni w soczewkach określamy tzw. zdolnością zbierającą. Zdolność zbierająca D soczewek
wyrażamy odwrotnością ogniskowej f
f
1
D
=
Jednostką zdolności zbierającej jest dioptria (m
-1
); soczewka o odległości ogniskowej f = 1m ma
zdolność zbierającą równą 1 dioptrii.
29.2. Metody wyznaczania ogniskowych soczewek cienkich.
A. Wyznaczanie ogniskowej soczewki skupiającej z pomiaru odległości przedmiotu i obrazu od
soczewki
Szczególnie proste, a równocześnie dostatecznie dokładne, są pomiary dokonywane za pomocą
ławy optycznej. Jest to zaopatrzona w podziałkę milimetrową szyna, wzdłuż której można dowolnie
przesuwać świecący przedmiot, soczewkę i ekran. Świecącym przedmiotem jest zwykle przesłona
w kształcie strzałki oświetlona od tyłu matową żarówką. Wystarczy dokonać na ławie optycznej
pomiaru odległości a oraz b (ale niezależnie od siebie), aby wyznaczyć wartość ogniskowej zgodnie
z przekształconym równaniem soczewki
b
a
b
a
f
+
=
(29.3)
B.
Wyznaczanie ogniskowej soczewki skupiającej metodą Bessela
Wielkości a i b występują w równaniu soczewki symetrycznie (można je przestawić bez zmiany
wartości wyrażenia na 1/f ). Gdy zrealizujemy w praktyce te dwa wzajemnie symetryczne ustawie-
nia przedmiotu i obrazu, to zauważymy, że odległość przedmiotu od obrazu pozostanie niezmienio-
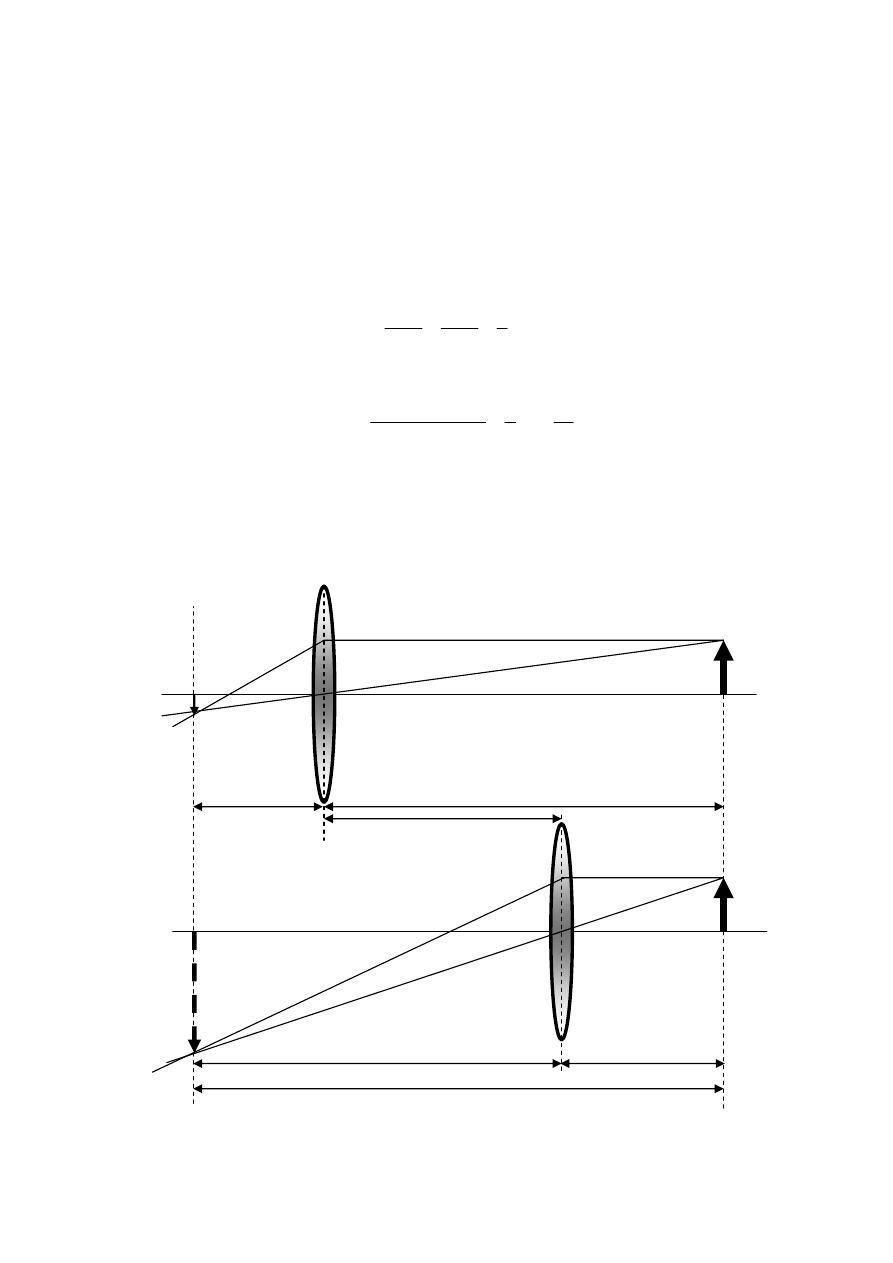
na, przy czym w pierwszym przypadku otrzymujemy obraz powiększony, a w drugim zaś – po-
mniejszony (rys. 29.3).
Jeżeli odległość przedmiotu od ekranu oznaczymy przez d odległość zaś między obu położeniami
soczewki przez c, to jak widać z rysunku
a + b = d
a – b = c
Wstawiając wartości a, b obliczone z powyższego układu do równania soczewki, otrzymamy
f
1
c
d
2
c
d
2
=
−
+
+
stąd
−
=
−
+
=
d
c
d
4
1
d
4
)
c
d
(
)
c
d
(
f
2
(29.4)
Ponieważ c
2
= d(d-4f) > 0, metodę tę można zastosować tylko wtedy, gdy d > 4f.
C
1
A
B’ F
B
A’
b
a
c
A
B’
F
B
A’
b’
C
2
a’
d
b’ = a
a’ = b
Rys. 29.3. Ilustracja pomiaru ogniskowej soczewki skupiającej metodą Bessela.
C.
Wyznaczanie ogniskowej soczewki rozpraszającej
Jak wynika z tabeli 29.1 soczewki rozpraszające tworzą obrazy pozorne, a więc takie, których nie
można uzyskać na ekranie. Wartość ogniskowej takich soczewek można wyznaczyć dwiema meto-
dami. Cechą wspólną tych metod jest utworzenie układu dwóch blisko położonych siebie soczewek:
rozpraszającej i skupiającej, który to układ posiada właściwości soczewki skupiającej o odpowied-
nio zmodyfikowanej wartości f. Zdolność skupiająca układu dwóch blisko położonych siebie so-
czewek o ogniskowej f
u
jest równa sumie zdolności skupiających poszczególnych soczewek o ogni-
skowych f
1
i f
2
2
1
U
f
1
f
1
f
1
+
=
(29.5)
Równanie to pozwala na obliczenie ogniskowej soczewki rozpraszającej f
2
pod warunkiem, że wy-
tworzony układ optyczny ma właściwości soczewki skupiającej, tzn. f
1
< f
2
(D
1
> D
2
)
U
1
1
U
2
f
f
f
f
f
−
=
(29.6)
Aby wyznaczyć f
2
należy uprzednio znać (zmierzyć) f
1
. Można jednak postąpić w inny sposób.
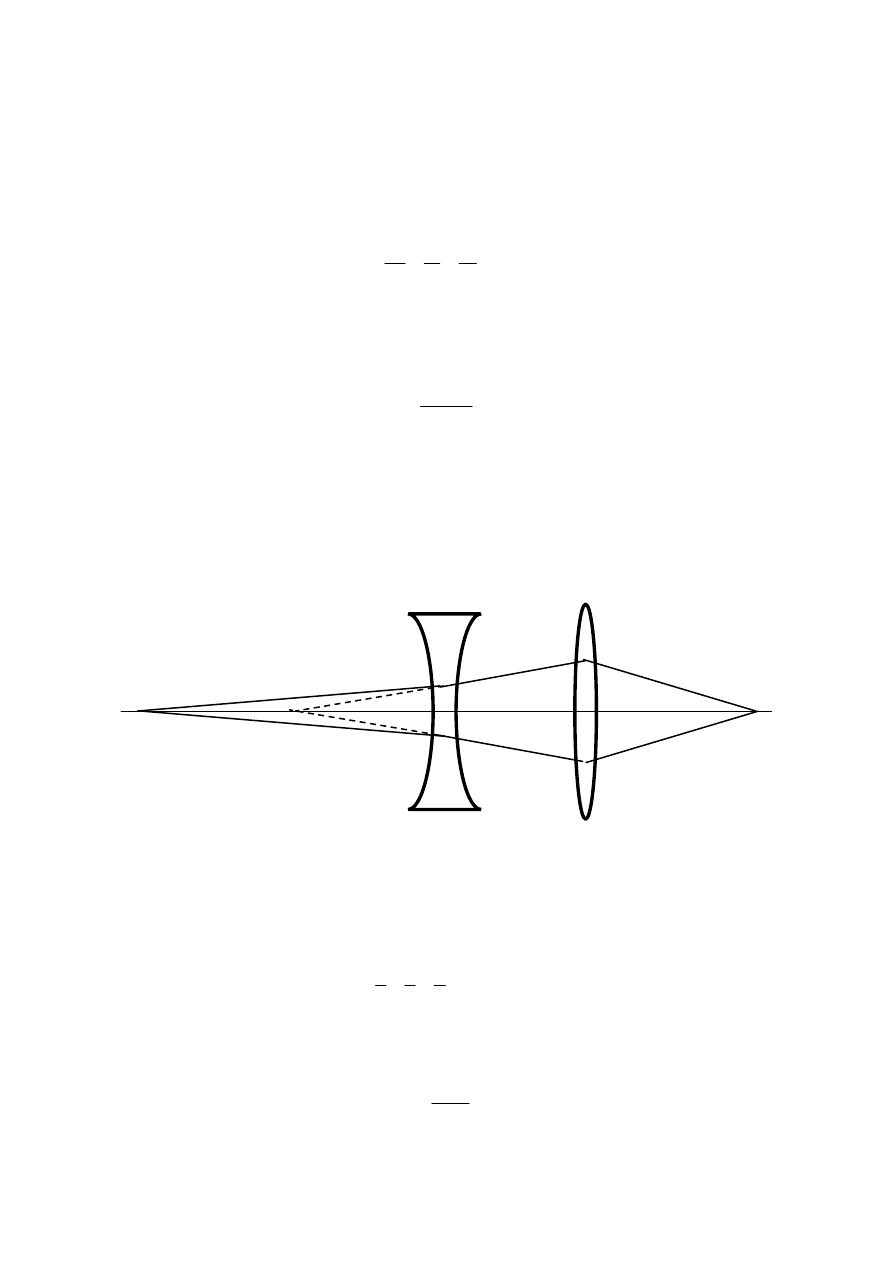
Jeśli na drodze promieni świetlnych wychodzących z punktu A i skupionych w punkcie D za pomo-
cą soczewki skupiającej, której środek optyczny znajduje się w punkcie B (rys.29.4), postawić so-
czewkę rozpraszającą o środku optycznym w punkcie C w taki sposób, że odległość CD byłaby
mniejsza od jej ogniskowej, to rzeczywisty obraz punktu A oddali się od soczewki B (np. do punktu
E).
E
A
D
C
B
Rys. 29.4. Ilustracja pomiaru ogniskowej soczewki rozpraszającej.
Punkt D jest urojonym obrazem punktu E otrzymanym za pomocą soczewki rozpraszającej. Ozna-
czając odległość EC = a, DC = b otrzymamy zgodnie z równaniem soczewki
b
1
a
1
f
1
−
=
−
(29.7)
gdzie b jest ujemne, bo mamy do czynienia z obrazem urojonym, stąd
b
a
b
a
f
−
=
(29.8)

29.3. Przebieg pomiarów
Pomiary przeprowadzamy wg metod przedstawionych w punkcie 29.2.
Ad A.
1. Umieścić na ławie optycznej pomiędzy ekranem a świecącym przedmiotem wskazaną przez wy-
kładowcę soczewkę skupiającą.
2. Przesuwając soczewkę otrzymać na ekranie ostry obraz przedmiotu.
3. Czynności wg punktu 2 powtórzyć 20 razy, za każdym razem dokonując niezależnego pomiaru a
lub b. Wielkości a i b powinny być zmierzone przynajmniej po 10 razy każda.
Ad B.
1. Ustalić położenie świecącego przedmiotu względem obrazu tak, by przez przesuwanie soczewki
skupiającej uzyskać na ekranie obraz powiększony a następnie pomniejszony.
2. Przesuwając ekranem otrzymać na ekranie powiększony ostry obraz. Czynność tę powtórzyć 10
razy, za każdym razem notując położenie ekranu. Wyznaczyć średnią odległość od przedmiotu
do ekranu d oraz średni błąd kwadratowy
d
σ
. Ustawić ekran w obliczonym położeniu (odle-
głość ta jest stała dla wszystkich pomiarów w punktach 3 i 4).
3. Regulując położeniem soczewki otrzymać na ekranie powiększony ostry obraz. Czynność tę
powtórzyć 10 razy, za każdym razem notując położenie C
1
soczewki.
4. Powtórzyć czynności wg punktu 3 dla obrazu pomniejszonego (położenie C
2
soczewki).
Ad C.
1. Między przedmiotem i ekranem umieścić soczewkę skupiającą.
2. Przesuwając ekran otrzymać na nim ostry obraz świecącego przedmiotu. Odnotować położenie
ekranu (punkt D). Czynność tę powtórzyć 10 razy.
3. Między ekranem a soczewką skupiającą umieścić soczewkę rozpraszającą (blisko soczewki
skupiającej – punkt C).
4. Przesuwając ekran ponownie otrzymać ostry obraz (punkt E). Czynność tę powtórzyć 10 razy
notując za każdym razem położenie ekranu.
29.4. Opracowanie wyników pomiarów.
Ad
A.
1. Obliczyć średnie arytmetyczne wartości a i b oraz ich średnie błędy kwadratowe
b
a
σ
σ
,
. Na
podstawie wzoru (29.3) obliczyć f.
2. Obliczyć średni błąd kwadratowy wartości ogniskowej f
2
4
2
4
2
f
)
(
1
a
b
a
b
b
a
σ
σ
σ
+
+
=

Ad B.
1. Wyznaczyć średnie arytmetyczne wartości położeń C
1
i C
2
oraz ich średnie błędy kwadratowe.
2. Wyznaczyć średnią wartość przesunięcia soczewki c jako różnicę pomiędzy średnimi położe-
niami C
1
i C
2
.
3. Obliczyć średni błąd kwadratowy przesunięcia
c
σ
jako sumę średnich błędów kwadratowych
wyznaczonych w punkcie 1. Przyjąć
d
σ
równe średniemu błędowi kwadratowemu wyznaczo-
nemu dla wartości położenia I (gdy obraz jest powiększony).
4. Korzystając ze wzoru (29.4) obliczyć ogniskową soczewki.
5. Obliczyć średni błąd kwadratowy wartości ogniskowej
2
2
2
2
2
2
f
d
c
4
d
c
1
4
1
c
d
σ
σ
σ
+
+
=
Ad C.
1. Obliczyć średnie arytmetyczne wartości a i b oraz ich średnie błędy kwadratowe
b
a
σ
σ
,
Na podstawie wzoru (29.8) obliczyć f.
2. Obliczyć średni błąd kwadratowy wartości ogniskowej f.
2
4
2
4
2
f
)
(
1
a
b
a
b
b
a
σ
σ
σ
+
+
=
29.5. Pytania kontrolne
1. Na podstawie równania soczewki omówić geometryczne warunki tworzenia obrazów: rzeczy-
wistego i pozornego (urojonego) dla soczewek skupiających i rozpraszających.
2. Jaka jest zależność wielkości obrazu od miejsca jego powstania.
3. Od czego zależy ogniskowa soczewek cienkich?
4. Zdefiniować zdolność zbierającą soczewki.
5. Omówić wady soczewek i układów optycznych.
6. Omówić metodę Bessela wyznaczania ogniskowej soczewek cienkich.
L i t e r a t u r a
[1] Bobrowski C.: Fizyka dla inżynierów. PWN, Warszawa 1981.
[2] Jeżewski M.: Fizyka. PWN, Warszawa 1970.
[3] Resnick R., Halliday D.: Fizyka, t.II. PWN, Warszawa 1973.
[4] Szczeniowski S.: Fizyka doświadczalna, cz.IV. Optyka. PWN, Warszawa 1971.
Wyszukiwarka
Podobne podstrony:
WYZNACZANIE OGNISKOWEJ SOCZEWEK ZA POMOCĄ ŁAWY OPTYCZNEJ0-2, Matematyka - Fizyka, Pracownia fizyczna
Wyznaczanie ogniskowych soczewek za pomocą ławy optycznej, Wyznaczanie ogniskowych soczewek za pomoc
Wyznaczanie ogniskowej soczewek za pomocą ławy optycznej4, I rok INFORMATYKA_
wyznaczanie ogniskowej za pomocą Ławy optycznej - 3, Wyznaczanie ogniskowych soczewek za pomoc? ?awy
Wyznaczanie ogniskowej soczewek za pomocą ławy optycznej
Fizyka, Wyznaczanie ogniskowej soczewki za pomocą ławy optycznej
20 Wyznaczanie ogniskowej soczewek za pomocą ławy optycznej Kamil
Wyznaczanie ogniskowej Soczewki za pomocą ławy optycznej Wstęp i wnioski
Wyznaczanie ogniskowej soczewek za pomoca lawy optycznej
2WYZNACZANIE OGNISKOWEJ SOCZEWEK ZA POMOCĄ ŁAWY OPTYCZNEJ 1
8Wyznaczanie ogniskowych soczewek za pomocą ławy optycznej
3wyznaczanie ogniskowej za pomocą Ławy optycznej 1 DOC
wyznaczanie ogniskowych soczewek za pomocą awy optycznej4
wyznaczanie ogniskowych soczewek za pomocą awy optycznej3, MIBM WIP PW, fizyka 2, sprawka fiza 2, f
więcej podobnych podstron