1)

DEFINICJA SCHEMATU DYNAMICZNEGO USTROJU BUDOWLANEGO
Schem. statyczny uzupełniony o informacje istotne z punktu widzenia dyn., czyli
opis wielkości i rozkładu mas, opis charakteru i rozkładu oporów ruchu
(tłumienia), opis zewnętrznych sił czynnych jako f-cji miejsca i czasu.

2)

CO NAZYWAMY LICZBĄ DYNAMICZNYCH STOPNI SWOBODY?
LDSS to liczba niezależnych wsp. Uogólnionych koniecznych do jednoznacznego
określenia w danej chwili położenia wszystkich p-tów masowych. Oblicza się ją
po myślowym usunięciu nieważkich więzi odkształcalnych, jako sumę wsp.
uogólnionych swobodnych el. masowych, od której odejmuje się liczbę
warunków nałożonych przez więzi nieodkształcalne.
Podział układów ze względu na LDSS:

a.

układy o 1 dyn. st swobody d=1

b.

układy dyskretne, 1<d≤n

c.

układy ciągłe, d=∞

3)

RÓWNANIE LAGRANGE’A DLA MAŁYCH DRGAŃ
Równanie Lagrange’a II-go rodzaju

𝑑

𝑑𝑡

𝛿𝐸𝑘
𝛿𝑞′𝑖

−

𝛿𝐸𝑘

𝛿𝑞𝑖

+

𝛿𝜙

𝛿𝑞′𝑖

+

𝛿𝐸𝑝

𝛿𝑞𝑖

=

𝛿𝐿

𝛿𝑞′𝑖

, 𝑖 = 1,2,3, … , 𝑛

𝑞̅ = 𝜔𝑙 (𝑞1, 𝑞2, 𝑞3, … , 𝑞𝑛)
𝑞′ = 𝜔𝑙 (𝑞′1, 𝑞′2, 𝑞′3, … , 𝑞′𝑛)

Dla małych drgań Ek jest tylko f-cją prędkości 𝐸𝑘 = 𝐸𝑘(𝑞

′

̅ ) ↪

𝛿𝐸𝑘

𝛿𝑞𝑖

= 0

𝑑

𝑑𝑡

𝑔𝑟𝑎𝑑

𝑞

′

𝐸𝑘 + 𝑔𝑟𝑎𝑑

𝑞

′

𝜙 + 𝑔𝑟𝑎𝑑

𝑞

𝐸𝑝 = 𝑔𝑟𝑎𝑑

𝑞

′

𝐿

np. 𝑔𝑟𝑎𝑑

𝑞

𝐸𝑝 = 𝜔𝑙 (

𝛿𝐸𝑝
𝛿𝑞1

,

𝛿𝐸𝑝
𝛿𝑞2

, … ,

𝛿𝐸𝑝
𝛿𝑞𝑛

)

4)

WYZNACZENIE MACIERZY PODATNOŚCI DLA UKŁ. SN.
W przypadku ukł. SN przecinamy więzi nadliczbowe i wprowadzamy na ich
kierunku dodatkowe współrzędne tworzące wektor x. Wektorowi temu
odpowiada wektor sił X. Tworzymy tzw. bazę poszerzoną.
𝑥̅, 𝑋̅; 𝑞̅, 𝑄̅

𝑞̅̌ = [𝑞̅

𝑥̅

] ; 𝑄̅̌ = [𝑄

̅

𝑋̅

] ; 𝐷̌

[𝑞̅

𝑥̅

] = [

𝐷𝑞𝑞 𝐷𝑞𝑥
𝐷𝑥𝑞 𝐷𝑥𝑥] [

𝑄̅
𝑋̅

]

wektor przemieszczeń w miejscu przeciętych więzi 𝑥̅ = 𝐷𝑥𝑞 ∙ 𝑄̅ + 𝐷𝑥𝑥 ∙ 𝑋̅ =
0̅ → 𝑋̅ = −𝐷𝑥𝑥

−1

∙ 𝐷𝑥𝑞 ∙ 𝑄̅

𝑞̅ = 𝐷𝑞𝑞 ∙ 𝑄̅ + 𝐷𝑞𝑥 ∙ 𝑋̅ → 𝑞̅ = 𝐷𝑞𝑞 ∙ 𝑄̅ + 𝐷𝑞𝑥 ∙ (−𝐷𝑥𝑥

−1

) ∙ 𝐷𝑥𝑞 ∙ 𝑄̅

= (𝐷𝑞𝑞 − 𝐷𝑥𝑥

−1

∙ 𝐷𝑞𝑥 ∙ 𝐷𝑥𝑞)𝑄̅ = 𝐷𝑄̅

𝐷 = 𝐷𝑞𝑞 − 𝐷𝑥𝑥

−1

∙ 𝐷𝑞𝑥 ∙ 𝐷𝑥𝑞

5)

WYZNACZENIE MACIERZY SZTYWNOŚCI DLA UKŁ. GN W SENSIE DYNAMICZNYM.
n

gd

>0 wprowadzamy dodatkowe współrzędne tworzące wektor X, opisujący

dodatkowe stopnie swobody siatki prętowej (ponad współrzędne dynamiczne)
Tworzymy bazę poszerzoną: 𝑞̅ – baza wyjściowa, 𝑄̅ – odpowiadający jej wektor

sił; 𝑞̅̌ =

𝑞̅

𝑥̅

𝑄̅̌ = 𝑄

̅

𝑋̅

Dla bazy poszerzone tworzymy macierz sztywności: 𝑄̅̌ = 𝐾

̌ ∙ 𝑞̅̌

[𝑄

̅

𝑋̅

] = [

𝐾𝑞𝑞 𝐾𝑞𝑥
𝐾𝑥𝑞 𝐾𝑥𝑥] [

𝑞̅

𝑥̅

]  𝑄̅ = 𝐾𝑞𝑞 ∙ 𝑞̅ + 𝐾𝑞𝑥 ∙ 𝑥̅, 𝑋̅ = 𝐾𝑥𝑞 ∙ 𝑞̅ + 𝐾𝑥𝑥 ∙ 𝑥̅ =

0  𝑋̅ = −𝐾𝑥𝑥

−1

∙ 𝐾𝑥𝑞 ∙ 𝑞̅

𝑄̅ = 𝐾𝑞𝑞 ∙ 𝑞̅ − 𝐾𝑞𝑥 ∙ 𝐾

𝑥𝑥

−1

∙ 𝐾

𝑥𝑞

∙ 𝑞̅ = (𝐾

𝑞𝑞

− 𝐾

𝑞𝑥

∙ 𝐾

𝑥𝑥

−1

∙ 𝐾

𝑥𝑞

) ∙ 𝑞̅ = 𝐾 ∙ 𝑞̅ 

𝐾 = 𝐾

𝑞𝑞

− 𝐾

𝑞𝑥

∙ 𝐾

𝑥𝑥

−1

∙ 𝐾

𝑥𝑞

6)

RÓWNANIA RUCHU OPISUJĄCE ZAGADNIENIE WŁASNE, DRGANIA SWOBODNE I
DRGANIA WYMUSZONE.
Zagadnienie własne:
𝑑 = 1; 𝑚𝑞̈ + 𝑘𝑞 = 0
𝑞(𝑡) = 𝑞̅𝑠 ∙ sin 𝜔𝑡 + 𝑞̅𝑐 ∙ cos 𝜔𝑡
𝑞̈(𝑡) = −𝜔

2

𝑞(𝑡)

1 ≤ 𝑑 < ∞; 𝐵𝑞̅̈ + 𝐾𝑞̅ = 0̅ ; 𝑞̅ = [𝑞1, 𝑞2, … , 𝑞𝑛] 𝑛 ≥ 𝑑
𝑞̅(𝑡) = 𝑞̅𝑠 ∙ sin 𝜔𝑡 + 𝑞̅𝑐 ∙ cos 𝜔𝑡
𝑞̅̈(𝑡) = −𝜔

2

𝑞̅(𝑡)

Drgania swobodne:
𝑑 = 1; 𝑚𝑞̈ + 𝑐𝑞̇ + 𝑘𝑞 = 0
1 ≤ 𝑑 < ∞; 𝐵𝑞̅̈ + 𝐶𝑞̅̇ + 𝐾𝑞̅ = 0̅ ; 𝑞̅ = [𝑞1, 𝑞2, … , 𝑞𝑛] 𝑛 ≥ 𝑑
Drgania wymuszone:
𝑑 = 1; 𝑚𝑞̈ + 𝑐𝑞̇ + 𝑘𝑞 = 𝑃(𝑡)
1 ≤ 𝑑 < ∞; 𝐵𝑞̅̈ + 𝐶𝑞̅̇ + 𝐾𝑞̅ = 𝐹̅ ; 𝑞̅ = [𝑞1, 𝑞2, … , 𝑞𝑛] 𝑛 ≥ 𝑑

7)

ZAGADNIENIE WŁASNE DLA UKŁ. DYSKRETNEGO: RÓWNANIA WYJŚCIOWE I
ROZW. ZAGADNIENIA WŁASNEGO(CZĘSTOŚCI WŁASNE I WEKTORY WŁASNE)
(Równanie wyjściowe)
1 ≤ 𝑑 < ∞; 𝐵𝑞̅̈ + 𝐶𝑞̅̇ + 𝐾𝑞̅ = 𝐹̅ ; 𝑞̅ = [𝑞1, 𝑞2, … , 𝑞𝑛] 𝑛 ≥ 𝑑
𝑞̅(𝑡) = 𝑞̅𝑠 ∙ sin 𝜔𝑡 + 𝑞̅𝑐 ∙ cos 𝜔𝑡
𝑞̅̈(𝑡) = −𝜔

2

𝑞̅(𝑡)

(Rozwiązanie zagadnienia własnego) (𝐾 − 𝜔

2

𝐵)𝑞̅ = 0̅

det(𝐾 − 𝜔

2

𝐵) = 0→ wtedy powyższe równ. ma rozwiązanieniezerowe

𝜆 = 𝜔

2

det(𝐾 − 𝜆𝐵)𝑞̅ = 𝑎

𝑑

𝜆

𝛼

+ 𝑎

𝑑−1

𝜆

𝛼−1

+ 𝑎

𝑑−2

𝜆

𝛼−2

+ ⋯ + 𝑎

1

𝜆 + 𝑎

0

= 0 (równanie

charakterystyczne)
𝜆

1

, 𝜆

2

, … , 𝜆

𝛼

𝜔

1

, 𝜔

2

, … , 𝜔

𝑑

- częstości drgań własnych

(𝜔

1

≤ 𝜔

2

≤ ⋯ ≤ 𝜔

𝑑

)

Każdej częstoświ 𝜔

𝑖

odpowiada rozwiązanie 𝑞̅ = 𝜔

̅

𝑖

(wektory własne)

(𝐾 − 𝜔

𝑖

2

𝐵)𝜔̅

𝑖

= 0̅

Można wykazać, że jeżeli częstość 𝜔

𝑖

jest jednokrotna to równanie jednorodne

jest spełnione przez każdą niezerową kolumnę macierzy dołączonej do macierzy
𝐾 − 𝜔

𝑖

2

𝐵

ω = (𝜔̅

1

, 𝜔̅

2

, … , 𝜔̅

𝛼

) = [

𝜔

11

𝜔

12

… 𝜔

1𝑛

𝜔

21

𝜔

22

… 𝜔

2𝑛

⋮⋮

⋱⋮

𝜔

𝑚1

𝜔

𝑚2

… 𝜔

𝑚𝑛

] 𝐵𝑎𝑧𝑎 𝑟ó𝑤𝑛𝑎𝑛𝑖𝑎 𝑛 = 𝑑, 𝑛 ≥ 𝑑

𝜔- macierz własna
𝐾𝜔 = 𝐵𝜔{𝜔

2

} {𝜔

2

} = 𝑑𝑖𝑎𝑔(𝜔

1

2

, 𝜔

2

2

, … , 𝜔

𝑑

2

)

8) ZASADA ORTOGONALNOŚCI DRGAŃ WŁASNYCH

Wychodząc z r.rów. dla zagadnienia własnego
𝐵𝑞̅̈ + 𝐾𝑞̅ = 0̅:

𝐾𝑊 = 𝐵𝑊{𝜔

2

} /∙ 𝑊

𝑇

𝑊

𝑇

𝐾𝑊 = 𝑊

𝑇

𝐵𝑊{𝜔

2

} /()

𝑇

𝑊𝐾𝑊

𝑇

= {𝜔

2

}𝑊𝐵𝑊

𝑇

Mnożenie {𝜔

2

} 𝑖 𝑊

𝑇

𝐵𝑊 jest przemienne, zatem 𝑊

𝑇

𝐵𝑊 = {𝑚

0

} −

𝑚. 𝑑𝑖𝑎𝑔
𝑊

𝑇

𝐾𝑊 = {𝑚

0

}{𝜔

2

} = {𝑘

0

}

, stąd:

𝑊

𝑗

𝑇

̅̅̅̅̅𝐵𝑊

𝑖

= 𝑚

𝑖

0

> 0 dla i=j, 𝑊

𝑗

𝑇

̅̅̅̅̅𝐵𝑊

𝑖

= 0 dla i≠j,

𝑊

𝑗

𝑇

̅̅̅̅̅𝐾𝑊

𝑖

= 𝑘

𝑖

0

> 0 dla i=j, 𝑊

𝑗

𝑇

̅̅̅̅̅𝐾𝑊

𝑖

= 0 dla i≠j,

Powyższe wzory opisują zas ortogonalności, która mówi, że

formy własne są do siebie ortogonalne z wagą B i K. W

przypadku, gdy częstości własne są jednokrotne, wówczas

rozwiązanie rów. Można uzyskać wyznaczając jedną z kolumn

macierzy dołączonej do macierzy 𝐾 − 𝜔

𝑖

2

𝐵 ; (𝐾 − 𝜔

𝑖

2

𝐵)𝑊

𝑖

̅̅̅ = 0̅,

9)

METODA TRANSFORMACJI WŁASNEJ ZASTOSOWANA DO ANALIZY DRGAŃ
WYMUSZONYCH HARMONICZNIE.
𝐵𝑞̅̈ + 𝐶𝑞̅̇ + 𝐾𝑞̅ = 𝑃̅(𝑡)
Dane jest równanie ruchu, przy czym macierz C bue nysu być konkretnie
określona (zakładamy, że podlega zasadzie ortogonalności), znane są natomiast
bezwymiarowe wsp. drgania γ

i

odpowiadające głównym formom drgań. Znane

jest ponadto rozwiazanie własne w zakresie częstości {ω } i wektorów własnych
W
𝑞̅ = 𝑊𝑦̅
𝜔

𝑇

𝐵𝑊𝑦̅̈ + 𝜔

𝑇

𝐶𝑊𝑦̅̇ + 𝜔

𝑇

𝐾𝑊𝑦̅ = 𝜔

𝑇

𝑃̅(𝑡) = 𝑌̅(𝑡)

{𝑚

0

}𝑦̅̈ + {𝛾√𝐾

𝑜

𝑚

𝑜

}𝑦̅̇ + {𝐾

𝑜

}𝑦̅ = 𝑌̅(𝑡)

𝑚

𝑖

0

𝑦̈

𝑖

+ 𝛾

𝑖

√𝐾

𝑜

𝑚

𝑜

𝑦̇

𝑖

+ {𝐾

𝑜

}𝑦

𝑖

= 𝑌

𝑖

(𝑡); 𝑖 = 1,2, … , 𝑛

Metoda transformacji własnej pozwala na rozseparowanie układu równań.
W szczególnym przypadku wymuszenia harmonicznego mamy:
𝑌̅ = 𝜔

𝑇

(𝑃

𝑆

𝑠𝑖𝑛𝑝𝑡 + 𝑃

𝐶

𝑐𝑜𝑠𝑝𝑡 = 𝑌

𝑆

̅ 𝑠𝑖𝑛𝑝𝑡 + 𝑌

𝐶

̅ 𝑐𝑜𝑠𝑝𝑡, 𝑦 = 𝑦

𝑠

𝑠𝑖𝑛𝑝𝑡 + 𝑦

𝑐

𝑐𝑜𝑠𝑝𝑡

10) METODA BEZPOŚREDNIA W ROZWIĄZANIU ZAGADNIENIA DRGAŃ

WYMUSZONYCH HARMONICZNIE DLA UKŁ. DYSKRETNEGO.
𝐵𝑞̅̈ + 𝐶𝑞̅̇ + 𝐾𝑞̅ = 𝑃̅(𝑡)
𝑃̅(𝑡) = 𝑃̅𝑠 ∙ sin 𝑝𝑡 + 𝑃̅𝑐 ∙ cos 𝑝𝑡 (p-częstość wymuszenia)
𝑞̅(𝑡) = 𝑞̅𝑠 ∙ sin 𝑝𝑡 + 𝑞̅𝑐 ∙ cos 𝑝𝑡
𝑞̅̇(𝑡) = 𝑝 ∙ (𝑞̅𝑠 ∙ cos 𝜔𝑡 − 𝑞̅𝑐 ∙ sin 𝜔𝑡)
𝑞̅̈(𝑡) = −𝑝

2

(𝑞̅𝑠 ∙ sin 𝑝𝑡 + 𝑞̅𝑐 ∙ cos 𝑝𝑡)

{

(𝐾 − 𝑝

2

𝐵)𝑞̅𝑠 − 𝑝𝐶𝑞̅𝑐 = 𝑃̅𝑠

𝑝𝐶𝑞̅𝑠 + (𝐾 − 𝑝

2

𝐵)𝑞̅𝑐 = 𝑃̅𝑐

[

𝐾 − 𝑝

2

𝐵

−𝑝𝐶

𝑝𝐶

𝐾 − 𝑝

2

𝐵

] [

𝑞̅𝑠

𝑞̅𝑐] = [

𝑃̅𝑠

𝑃̅𝑐

] → 𝑞̅𝑠, 𝑞̅𝑐

(𝐾 − 𝑝

2

𝐵)𝑞̅𝑠, 𝑐 = 𝑃̅𝑠, 𝑐

𝐷𝐵𝑞̅̈ + 𝐷𝐶𝑞̅̇ + 𝑞̅ = 𝐷𝑃̅

[

𝐼 − 𝑝

2

𝐷𝐵

−𝑝𝐷𝐶

𝑝𝐷𝐶

𝐼 − 𝑝

2

𝐷𝐵

] [

𝑞̅𝑠

𝑞̅𝑐] = [

𝐷𝑃̅𝑠

𝐷𝑃̅𝑐

]

(𝐼 − 𝑝

2

𝐷𝐵)𝑞̅𝑠, 𝑐 = 𝐷𝑃̅𝑠, 𝑐

11) OBWIEDNIA DYNAMICZNYCH SIŁ WEWNĘTRZNYCH W PRZYPADKU DRGAN

HARMONICZNYCH
Obwiednia sił dynamicznych jest zawsze symetryczna,
przyjmuje wartości amM lub –amM
𝑎𝑚𝑀 = ∓√𝑀

𝑠

2

+ 𝑀

𝑐

2

, indeks s – składowa sinusowa, c-cosinusowa

W rzeczywistości obwiednia momentów czy innych sił wew.

Nigdy nie jest symetryczna ze względu na występowanie sił

wew od obc stałych

12) ROZW. ZAGADNIENIA DRGAŃ WYMUSZONYCH HARMONICZNIE DLA O UKŁ. D=1

(ROZWIĄZANIE + WYKRESY)
𝑚𝑞̈ + 𝑐𝑞̇ + 𝑘𝑞 = 𝑃𝑠 ∙ sin 𝑝𝑡 + 𝑃𝑐 ∙ cos 𝑝𝑡 (p-częstość wymuszenia)

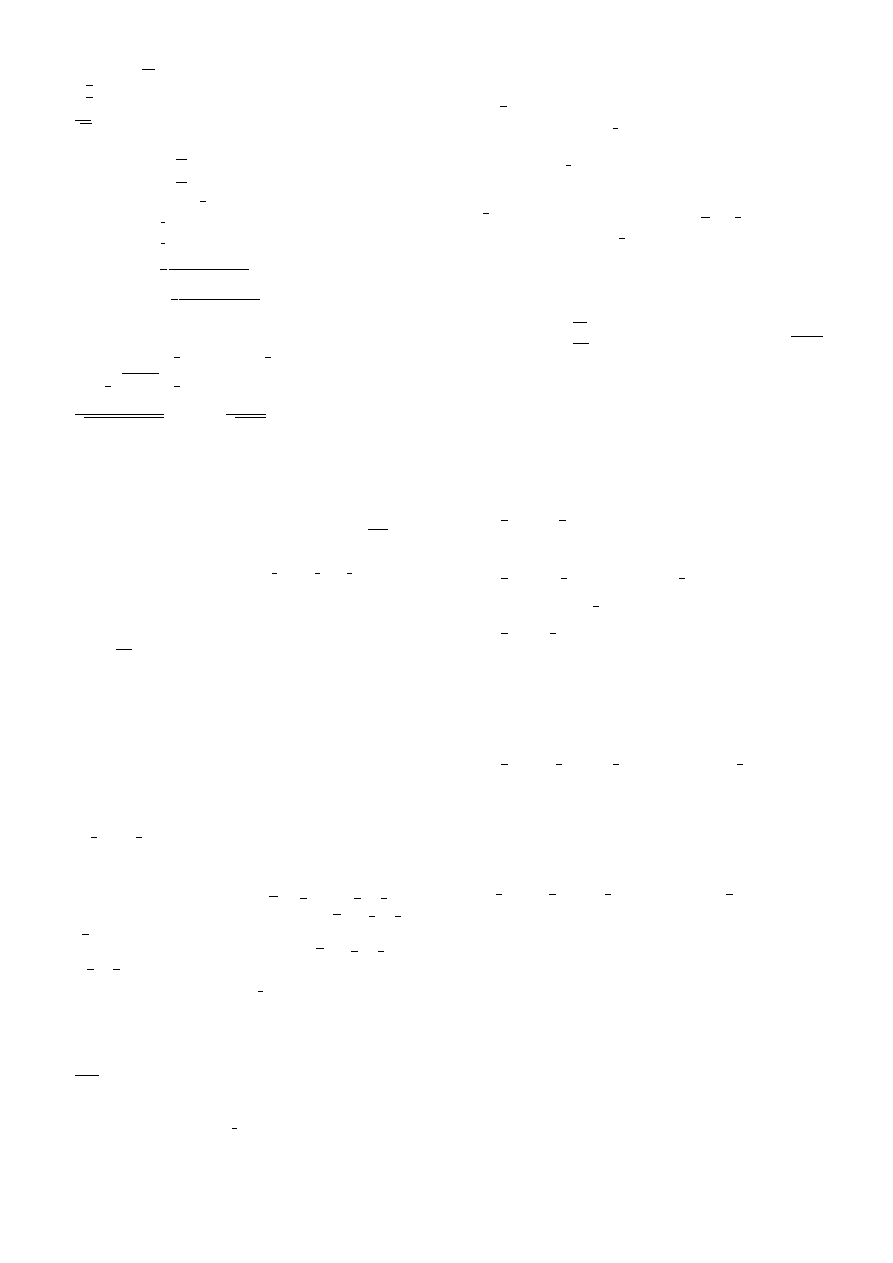
𝑞̈ + 𝛾𝜔𝑞̇ + 𝜔

2

𝑞 =

𝜔

2

𝑘

(𝑃𝑠 ∙ sin 𝑝𝑡 + 𝑃𝑐 ∙ cos 𝑝𝑡)

𝜔 = √

𝑘

𝑚

→ częstość drgań własnych

𝛾 =

𝑐

√𝑘𝑚

→ bezwymiarowy wsp. tłumienia

𝑞(𝑡) = 𝑞̅𝑠 ∙ sin 𝑝𝑡 + 𝑞̅𝑐 ∙ cos 𝑝𝑡

{

(𝜔

2

− 𝑝

2

)𝑞𝑠 − 𝛾𝑝𝜔𝑞𝑐 =

𝜔

2

𝑘

(𝑃𝑠 ∙ sin 𝑝𝑡 + 𝑃𝑐 ∙ cos 𝑝𝑡)|: 𝜔

2

𝛾𝑝𝜔𝑞𝑠 + (𝜔

2

− 𝑝

2

)𝑞𝑐 =

𝜔

2

𝑘

(𝑃𝑠 ∙ sin 𝑝𝑡 + 𝑃𝑐 ∙ cos 𝑝𝑡)|: 𝜔

2

Wprowadzamy oznaczenie 𝜂 =

𝑝

𝜔

{

(1 − 𝜂

2

)𝑞𝑠 − 𝛾𝜂𝑞𝑐 =

1
𝑘

𝑃𝑠

𝛾𝜂𝑞𝑠 + (1 − 𝜂

2

)𝑞𝑐 =

1
𝑘

𝑃𝑐

𝑞𝑠 = ℎ𝑃𝑠 + ℎ

′

𝑃𝑐; ℎ =

1
𝑘

1 − 𝜂

2

(1 − 𝜂

2

)

2

+ 𝛾

2

𝜂

2

𝑞𝑐 = −ℎ′𝑃𝑠 + ℎ𝑃𝑐; ℎ′ =

1
𝑘

𝛾𝜂

(1 − 𝜂

2

)

2

+ 𝛾

2

𝜂

2

Ostatecznie mamy:
𝑞(𝑡) = 𝑃𝑠(ℎ sin 𝑝𝑡 + ℎ

′

cos 𝑝𝑡) + 𝑃𝑐(ℎ

′

sin 𝑝𝑡 + ℎ cos 𝑝𝑡)

=

𝑣
𝑘

𝑃𝑠 sin(𝑝𝑡 − 𝜓) +

𝑣
𝑘

𝑃𝑐 cos(𝑝𝑡 − 𝜓)

𝑎𝑚𝑞(𝑡) =

𝑣
𝑘

√𝑃

𝑆

2

+ 𝑃

𝑐

2

=

𝑣
𝑘

𝑎𝑚𝑃

𝑣 =

1

√(1 − 𝜂

2

)

2

+ 𝛾

2

𝜂

2

; 𝜓 = 𝑎𝑟𝑐𝑡𝑔

𝛾𝜂

√1 + 𝛾

2

𝑣-wsp. dynamiczny

13) BEZWŁADNOŚCIOWE WZBUDZANIE DRGAŃ – UKŁAD O D=1.

model ustroju, w którym źródłem wzbudzenia jest maszyna

wirnikowa nazywamy wymuszeniem bezwładnościowym.
Rozważmy układ przedstawiony na rysunku poniżej, w którym masa m

o

, będąca

częścią masy m, wykonuje ruch obrotowy na mimośrodzie e z prędkością
kątową p. Podczas takiego ruchu powstaje siła odśrodkowa:

𝑃

0

= 𝑚

0

(𝑝𝑒)

2

𝑒

=

𝑚

0

𝑒𝑝

2

= 𝑀

0

𝑝

2

, przy czym M

0

= m

0

e jest masowym momentem niewyważenia

obrotowego. Rzut wirującej siły odśrodkowej na kierunek drgań określa wzór:
𝑃(𝑡) = 𝑃

0

𝑐𝑜𝑠𝑝𝑡 = 𝑀

0

𝑝

2

𝑐𝑜𝑠𝑝𝑡 , a więc 𝑎𝑚𝑞 =

𝑣
𝑘

𝑎𝑚𝑝 =

𝑣
𝑘

𝑝

0

=

𝑣
𝑘

𝑀

0

𝑝

2

.

Stosujemy wzór Kelvina –Voigta:

𝑎𝑚𝑄 = 𝑣

′

𝑎𝑚𝑃 = 𝑣

′

𝑀

0

𝑝

2

.

Opisany układ może być modelem ustroju, w którym źródłem wzbudzenia jest
maszyna wirnikowa. Wzbudzenie tego typu nazywamy wymuszeniem
bezwładnościowym. Po przekształceniach:

𝑎𝑚𝑞 = 𝑣𝜂

2

(

𝑀𝑜

𝑚

) , 𝑎𝑚𝑄 = 𝑣

′

𝜂

2

(𝑀𝑜 ∙ 𝜔

2

)

14) DRGANIA WYMUSZONE KINEMATYCZNIE – UKŁAD O D=1

Rozważmy układ przedstawiony na rysunku poniżej. Ruch jest

wymuszony określonymi drganiami q

0

(t) wykonywanymi przez

ostoję. Masa m wykonuje ruch złożony ze składowej

kinematycznej q

0

(t) oraz składowej względnej q(t). Równanie

ruchu ma postać:

𝑚(𝑞̈ + 𝑞̈

0

) + 𝑐𝑞̇ + 𝑘𝑞 = 0

𝑚𝑞̈ + 𝑐𝑞̇ + 𝑘𝑞 = −𝑚𝑞

0

̈ = 𝑃(𝑡)

Zakładamy, że 𝑞

0

= 𝑄𝑠𝑖𝑛𝑝𝑡

𝑚𝑞̈ + 𝑐𝑞̇ + 𝑘𝑞 = −𝑚𝑎𝑝

2

𝑠𝑖𝑛𝑝𝑡

𝑃(𝑡) = 𝑚𝑎𝑝

2

𝑠𝑖𝑛𝑝𝑡

𝑞(𝑡) = 𝑎𝑚𝑞𝑠𝑖𝑛(𝑝𝑡 − 𝜓)
𝑎𝑚𝑞 =

𝑣
𝑘

𝑎𝑚𝑝 =

𝑣
𝑘

𝑚𝑎𝑝

2

= 𝑣𝜂

2

𝑎

𝑞(𝑡) = 𝑣𝜂

2

𝑎𝑠𝑖𝑛 (𝑝𝑡 − 𝜓)

15) WARIANTY MODELU TŁUMIENIA DLA UKŁ. DYSKTETNYCH I DEF.

ODPOWIADAJACYM IM OBCIĄŻEŃ KINETYCZNYCH

- zewnętrzy charakter oporów ruchu: 𝐶 = 𝜇𝐵, 𝑄 = 𝐾𝑞 = 𝐹 − 𝐵(𝑞̈ + 𝜇𝑞̇)

- model Voighta-Kelvina (tłumienia wewnętrznego) 𝐶 = κ𝐾, 𝑄 = 𝐾(𝑞 + 𝜅𝑞̇) =
𝐹 − 𝐵𝑞̈
- wariat kombinowany, bliższy badaniom 𝐶 = 𝜇𝐵 + κ𝐾, 𝑄 = 𝐾(𝑞 + 𝜅𝑞̇) =
𝐹 − 𝐵(𝑞̈ + 𝜇𝑞̇) + wykres 𝛾(𝜔)
- model ze zmiennym czasem retardacji 𝜅 =

𝑋
𝑃

16) WSPÓŁCZYNIK DYNAMICZNY (DEF, WZÓR, WYKRES KRZYWEJ REZONANSOWEJ)

v-określa stosunek przemieszczeń dynamicznych do przemieszczeń statycznych,
wywołanych równym co do wartości obciążeniem, w przypadku pomijalnego
tłumienia v=1
𝑣 =

1

|1−𝜂

2

|

, przypadek η=1 odpowiadający równości 𝑝 = 𝜔 nazywamy stanem

rezonansowym – rezonansem
p-częstość kołowa drgań wymuszonych, 𝜔- częstość kołowa drgań własnych
rezonansowe opóźnienie fazowe: 𝜓 =

𝜋
2

nie zależy od wartości tłumienia,

natomiast rezonansowy współczynnik dynamiczny 𝑣 = 1/𝛾 gdy układ jest
tłumiony

17) PRZEDSTAWIĆ OMAWIANE PRZYPADKI DRGAŃ WYMUSZONYCH

APERIODYCZNIE
- 𝐹(𝑡) = 𝑃 ∙ 𝐻(𝑡), przypadek siły wzb. o stałej wartości P przyłożonej w chwilo

t=0 𝑚𝑞̈ + 𝑘𝑞 = 0
𝑞(𝑡) = 𝑞

𝑠

𝑠𝑖𝑛𝜔𝑡 + 𝑞

𝑐

𝑐𝑜𝑠𝜔𝑡 +

𝑃
𝑘

zakładając zerowe warunki początkowe,

otrzymamy qs=0 oraz qc=-P/k

ostatecznie: 𝑞(𝑡) =

𝑃
𝑘

(1 − 𝑐𝑜𝑠𝜔𝑡), obciążenie kin. 𝑄(𝑡) = 𝑘𝑞 = 𝑃(1 − 𝑐𝑜𝑠𝜔𝑡)

- 𝐹(𝑡) = 𝑃

𝑜

∙ 𝑡  działanie siły narastającej liniowo od zera z wydatkiem Po na

jednostkę czasu
𝑚𝑞̈ + 𝑘𝑞 = 𝑃(𝑡) = 𝑃

𝑜

𝑡  rozwiązanie rr 𝑞(𝑡) =

𝑃

0

𝑘

(𝑡 −

1

𝜔

𝑠𝑖𝑛𝜔𝑡), obc

kinetycze: 𝑄(𝑡) = 𝑘𝑞 = 𝑃

0

(𝑡 −

1

𝜔

𝑠𝑖𝑛𝜔𝑡)

-sila wzbudzająca w formie dowolnej, całkowalnej f-cji czasu, siłę dzieliy
myślowo na różniczkowe impulsy
przyjmując zerowe warunki początkowe otrzymamy rozwiązanie w podtaci całki
Duhamela:

bez tłumienia:𝑞(𝑡) =

1

𝑚𝜔

∫ 𝐹(𝜏)𝑠𝑖𝑛𝜔(𝑡 − 𝜏)𝑑𝜏

𝑡

0

z tłumieniem:

𝑞(𝑡) =

1

𝑚𝜔′

∫ 𝐹(𝜏)𝑒

−𝛼𝜔(𝑡−𝜏)

𝑠𝑖𝑛𝜔′(𝑡 − 𝜏)𝑑𝜏

𝑡

0

,

𝜔

′

= 𝜔√1 − 𝛼

2

18) WYPROWADZENIE MACIERZOWYCH WSP. RÓWNANIA RUCHU METODĄ

BILANSU ENERGETYCZNEGO
Macierz bezwładności B

𝐵 =

[

𝑏

11

𝑏

12

… 𝑏

1𝑗

𝑏

21

𝑏

22

… 𝑏

2𝑗

⋮⋮

⋱⋮

𝑏

𝑖1

𝑏

𝑖2

… 𝑏

𝑖𝑗

]

𝐵

𝑇

= (𝐴𝑚

𝑇

{𝑚}𝐴𝑚)

𝑇

= 𝐵(macierz symetryczna)

𝑢̅ = [𝑢1, 𝑢2, 𝑢3, … , 𝑢𝑛]

𝑇

{𝑚} = 𝑑𝑖𝑎𝑔(𝑚1, 𝑚2, 𝑚3, … , 𝑚𝑛)

𝐸𝑘 =

1
2

∑𝑚

𝑗

𝑢

𝑗

2

=

1
2

𝑢̅̇

𝑇

{𝑚}𝑢̅̇

𝑢̅ = 𝐴𝑚𝑞̅
Uwzględniając transformację otrzymujemy

𝐸𝑘 =

1
2

𝑢̅̇

𝑇

{𝑚}𝑢̅̇ =

1
2

(𝐴𝑚 ∙ 𝑞̅̇)

𝑇

{𝑚}𝐴𝑚 ∙ 𝑞̅̇ =

1
2

𝑞̅̇

𝑇

(𝐴𝑚

𝑇

∙ {𝑚} ∙ 𝐴𝑚) ∙ 𝑞̅̇

=

1
2

𝑞̅̇

𝑇

𝐵 ∙ 𝑞̅̇

𝐸𝑘 =

1
2

𝑞̅̇

𝑇

𝐵𝑞̅̇ =

1
2

∑𝑏

𝑖𝑗

𝑞̅̇

𝑖

𝑞̅̇

𝑗

Macierz sztywności K

𝐾 =

[

𝑘

11

𝑘

12

… 𝑘

1𝑛

𝑘

21

𝑘

22

… 𝑘

2𝑗

⋮⋮

⋱⋮

𝑘

𝑖1

𝑘

𝑖2

… 𝑘

𝑖𝑗

]

𝐾

𝑇

= 𝐾

𝐷𝐾 = 𝐾𝐷 = 𝐼 (D-macierz sztywności)

𝐸𝑝 =

1
2

∑𝑘

𝑗

𝑢

𝑗

2

=

1
2

𝑢̅

𝑇

{𝑘}𝑢̅̇ =

1
2

𝑞̅

𝑇

(𝐴𝑘

𝑇

∙ {𝑘} ∙ 𝐴𝑘) ∙ 𝑞̅ =

1
2

𝑞̅

𝑇

𝐾 ∙ 𝑞̅

Macierz tłumienia C

𝐶 =

[

𝑐

11

𝑐

12

… 𝑐

1𝑛

𝑐

21

𝑐

22

… 𝑐

2𝑗

⋮⋮

⋱⋮

𝑐

𝑖1

𝑐

𝑖2

… 𝑐

𝑖𝑗

]

𝐶

𝑇

= 𝐶

{𝑐} = 𝑑𝑖𝑎𝑔(𝑐1, 𝑐2, 𝑐3, … , 𝑐𝑛)

𝜙 =

1
2

∑𝑐

𝑗

𝑢̇

𝑗

2

=

1
2

𝑢̅̇

𝑇

{𝑐}𝑢̅̇ =

1
2

𝑞̅̇

𝑇

(𝐴𝑐

𝑇

∙ {𝑐} ∙ 𝐴𝑐) ∙ 𝑞̅̇ =

1
2

𝑞̅̇

𝑇

𝐶 ∙ 𝑞̅̇

19) ZAGADNIENIE DRGAŃ FUND. BLOKOWEGO NA PODŁOŻU SPRĘŻYSTYM