UKŁADY DYNAMICZNE

Uzasadnić wpływ wartości wymuszenia skokowego na odpowiedź układu różniczkującego rzeczywistego, podać jego tansmintancję.

Odpowiedź na wymuszenie skokowe wyznaczamy z transmintancji.

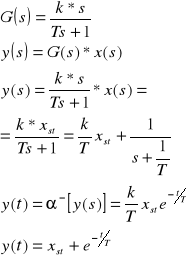
Zależność wartości wymuszenia skokowego i odpowiedzi jest liniowa , gdyż wymuszenia jest wprost proporcjonalne do odpowiedzi . Im większe wymuszenie tym większy spadek wartości odpowiedzi w jednostce czasu.

Y X

x_st

y(s)

T

T

Licznik - jest to urządzenie do zliczania impulsów elektrycznych (mogą zarówno dodawać jak i odejmować w zależności od wartości sygnałów). Układem dynamicznym nazywamy dowolny układ fizyczny rozpatrywany z punktu widzenia zachodzących w nim procesów dynamicznych.(przedstawianych za pomocą liniowych równań różniczkowych zwyczajnych o stałych parametrach) Ściśle wchodzą zależności pomiędzy przebiegami czasowymi zmiennych, a nie ich wartości chwilowych.

Stan układu -jest to zbiór wielkości dostarczających taką ilość informacji, które wystarczają do oceny zachowania się obiektu w przyszłości, czyli do jednoznacznego określenia zachowania się układu.

Dynamiczny układ liniowy i stacjonarny może być opisany przez n równań różniczkowych I-go rzędu.

x(t)=Ax(t)+Bu(t)

y(t)=Cx(t)+Du(t)

Sterowalność oznacza możliwość osiągnięcia dowolnego stanu układu w skończonym czasie za pomocą dopuszczalnego sterowania.

Dopuszczalne sterowanie-jest to sterowanie ograniczone przedziałami i ciągłe.

Warunkiem koniecznym i dostatecznym sterowalności jest, aby macierz S=[B,AB,A²B,...,A^n-1B] o n wierszach i m kolumnach była rzędu n ,czyli aby miała n liniowo niezależnych kolumn.

Obserwowalność oznacza , że na podstawie przebiegu sygnału wyjściowego w skończonym przedziale czasu można określić stan układu w tym przedziale. Warunkiem koniecznym i dostatecznym obserwowalności jest, aby macierz

C

AC

O= A²C

C...)

A^N-1C o wymiarach n*n była rzędu n , czyli zawierała n-liniowo niezależnych wierszy.

Ocena sterowalności i obserwowalności może być przeprowadzona na podstawie analizy:

• postaci kanonicznej równania stanu i równania wyjścia;

• bezpośredniej analizy schematu blokowego,

Układ jest stabilny ,gdyż dla stałej skończonej wartości zakłócenia i dla dowolnego stanu początkowego.

Sygnał wyjściowy będzie dążył do skończonej wartości ustalonej.

Układ jest sterowalny - jeżeli dla każdego t₀ istnieje takie sterowanie x(t), które spowoduje w skończonym przedziale czasu (t_k-t₀) przejście układu z dowolnego stanu początkowego u(t₀)=U₀ do stanu końcowego u(t_k)=U_k=0

Układ jest obserwowalny - w przedziale czasu t₀<t<t_k jeżeli na podstawie znajomości wejść (sterowań) x(t) i wektora wyjść y(t) w tym przedziale można wyznaczyć wektor stanu U₀ układu w chwili t₀. Warunkiem koniecznym i dostatecznym obserwowalności jest aby podany rząd macierzy był równy (n) wymiarowy wektora stanu.

Układ jest stabilny - gdy części rzeczywiste pierwiastków równania charakterystycznego są ujemne N(s)=s^2+s+1 S(1,2)= -0,5+/-j~3/2 Re(S12)=-0,5 Zamknięty układ liniowy jest stabilny, gdy dla stałej skończonej wartości zakłócenia i dla dowolnego stanu początkowego sygnał wyjściowy będzie dążył do skończonej wartości ustalonej. Lokalne - po przekroczeniu granicy x1 x2 układ się wróci do stanu poprzedniego i jest niestabilny. Będzie lokalnie jeżeli dla każdego dowolnie małego obszaru e można dobrać taki obszar r₀ stanów początkowych, że cała trajektoria stanu układu x(t) dla warunków początkowych zwartych w obszarze r₀ będzie zawarta także w obszarze e.

Globalnie - (o równaniu X'=Ax) wtedy i tylko wtedy gdy wszystkie wartości własne macierzy A mają niedodatnie części rzeczywiste i każda wartość własna o zerowej części rzeczywistej jest pierwiastkiem jednorodnym wielomianu. Stabilność punktu równowagi przy dowolnie dużych warunkach początkowych nazywa się globalną.

Asymptotyczna - jeżeli wektor stanu powróci do stanu równowagi.

Kryteria stabilności - analityczne (Hurwitza, Roughta) graficzne (Nequista) anal-graf (Michajłowa)

Stabilność lokalną rozumiemy stabilność tylko w punkcie równowagi bez określenia zakresu sygnałów zaburzających, po ustąpieniu których układ wraca do równowagi. Mówiąc o stabilności globalnej określamy jednocześnie obszar sygnałów zaburzających, po przejściu których układ zachowuje swój pierwotny stan równowagi. Jeżeli obszar stabilności globalnej obejmuje wszystkie możliwe sygnały wejściowe - totalna

Wartość A22 elementu macierzy A ma wpływ na tłumienie amplitudy odpowiedzi A12 na częstość oscylacji A11 zwiększa amplitudę odpowiedzi. Macierz A obrazuje wszystkie połączenia „skrośne” pomiędzy poszczególnymi zmiennymi stanami na wejściach integratorów. B,C i D wyraża połączenia typu „każdy z każdym” odpowiednich zmiennych. A-n*n - macierz procesu , stanu, stanu (układu)B-n*r - wymuszenia (wejścia, sterowania) C-m*n - odpowiedzi (wyjścia) D-m*r - transmisyjna u(t) - wektor wymuszenia , x(t) - wektora stanu x(t) y(t) - wektor odpowiedzi.

---