Wydział Automatyki, Elektroniki i Informatyki, rok akademicki 2009/10 semestr letni

Laboratorium KWPD

Laboratorium 4:

PROCESY DECYZYJNE W POSTACI

EKSTENSYWNEJ O SUMIE ZEROWEJ

Sprawozdanie wykonali:

Krzysztof Dendzik

Krzysztof Kucharski

AiR gr 1 TI

1. Wstęp

Zagadnieniem omawianym podczas ćwiczeń laboratoryjnych były
procesy ekstensywne, zatem procesy, które opisywane są nie za pomocą
macierzy, ale drzewa decyzyjnego. Taki rodzaj opisu jest podyktowany
niemożnością opisania za pomocą macierzy wszystkich reguł gry, takich
jak np. porządek podejmowania przez decydentów decyzji, poziom ich
wiedzy na kolejnych etapach gry, czy też rozwoju sytuacji w czasie
(dynamiki gry).

Drzewo decyzyjne składa się z wierzchołków, wśród których na
szczególną uwagę zasługuje korzeń, czyli wierzchołek znajdujący się na
samym szczycie drzewa oznaczający początek procesu. Wierzchołki
połączone są ze sobą łukami. W naszym przypadku podczas
rozpatrywania gry 3 etapowej w ostatnim fragmencie drzewa będziemy
mieli do czynienia z 64 (2

6

) wierzchołkami, którym przyporządkowane

będą wartości liczbowe. Dodatkowo, ponieważ zajmujemy się procesami
o sumie zerowej, to zadaniem jednego gracza będzie maksymalizacja
wskaźnika jakości, podczas, gdy zadaniem drugiego- minimalizacja.
Drzewo, którym będziemy się zajmować jest spójne (nie występują
elementy niepołączone z główną strukturą) oraz acykliczne (nie występują
zapętlenia.

2. Przykładowy problem wieloetapowy o liczbie etapów K=3

Opis problemu:

Podczas wyborów prezydenckich w USA o elekcję stara się dwóch
kandydatów: jeden z ramienia partii Republikanów, drugi z ramienia
partii Demokratów. Podczas kampanii zapowiedziano 3 debaty
prezydenckie, podczas których kandydaci będą wspólnie odpowiadali na
zadane przez prowadzącego pytanie oraz wzajemnie się przepytywali.
Przed pierwszą kampanią nastroje społeczne kształtują się w następujący
sposób: każdy z kandydatów ma mniej więcej 30 % poparcia, 40 %
pytanych osób nie ma jeszcze wyrobionego zdania. Obaj kandydaci zdają
sobie sprawę, że „przechodzenie” wyborców z jednego kandydata na
drugiego będzie znikome i walka między nimi rozstrzygnie się wśród
osób niezdecydowanych. Przed każdą debatą każdy z kandydatów
przygotowuje strategię: może skupić się na osobach młodych
(i obiecywać spełnienie ich postulatów) lub też na osobach powyżej 40

lat. Co prawda obaj kandydaci występują równocześnie, ale podczas danej
debaty nie mogą zmienić wcześniej obranej taktyki (której przygotowanie
zajmuje sporo czasu), zatem możemy uznać, że gracze nie wiedzą
wcześniej o tym, jak postąpi ich konkurent. Wskaźnik jakości uzyskany
na końcowych wierzchołkach oznacza różnicę punktów procentowych,
jakie zyskał kandydat drugi względem kandydata pierwszego po całym
cyklu debat (np. jeśli po debatach na kandydata A będzie chciało
głosować 45% osób a na kandydata B 35, to wskaźnik wyniesie 10,
ponieważ A zyskał 15 punktów procentowych, a B 5, różnica tych liczb to
właśnie 10).

M- prowadzenie debaty w sposób atrakcyjniejszy dla młodszych
wyborców

S- prowadzenie debaty w sposób atrakcyjniejszy dla starszych wyborców

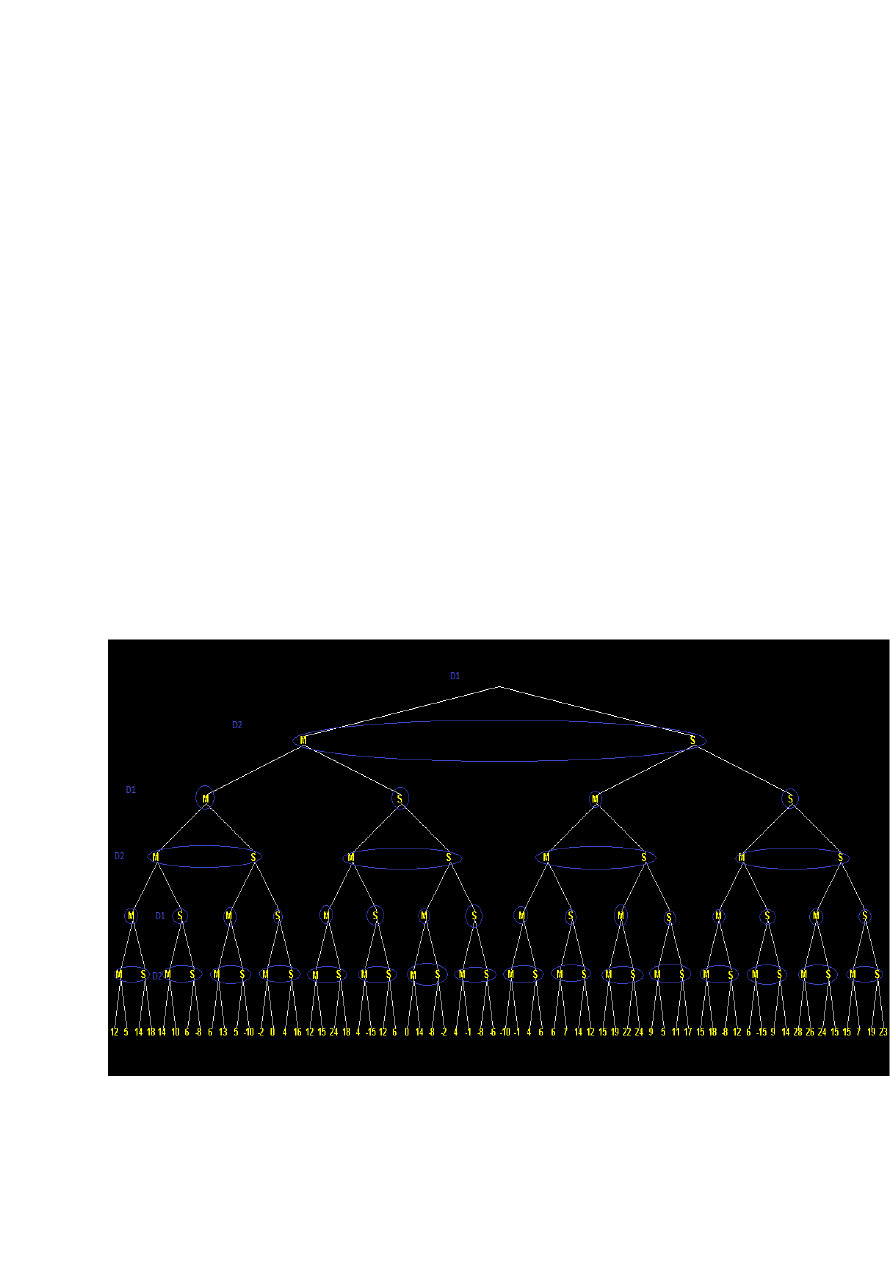
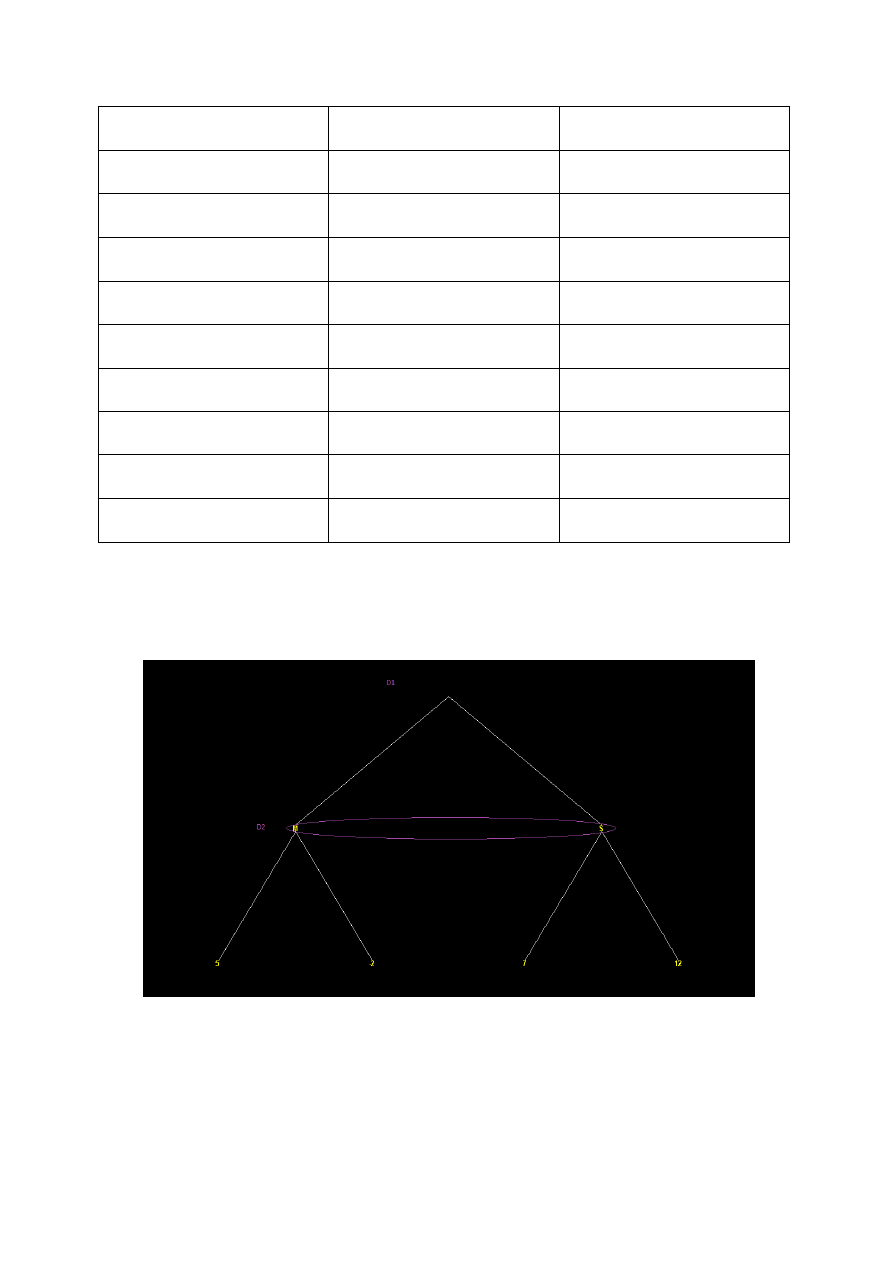
Drzewo:

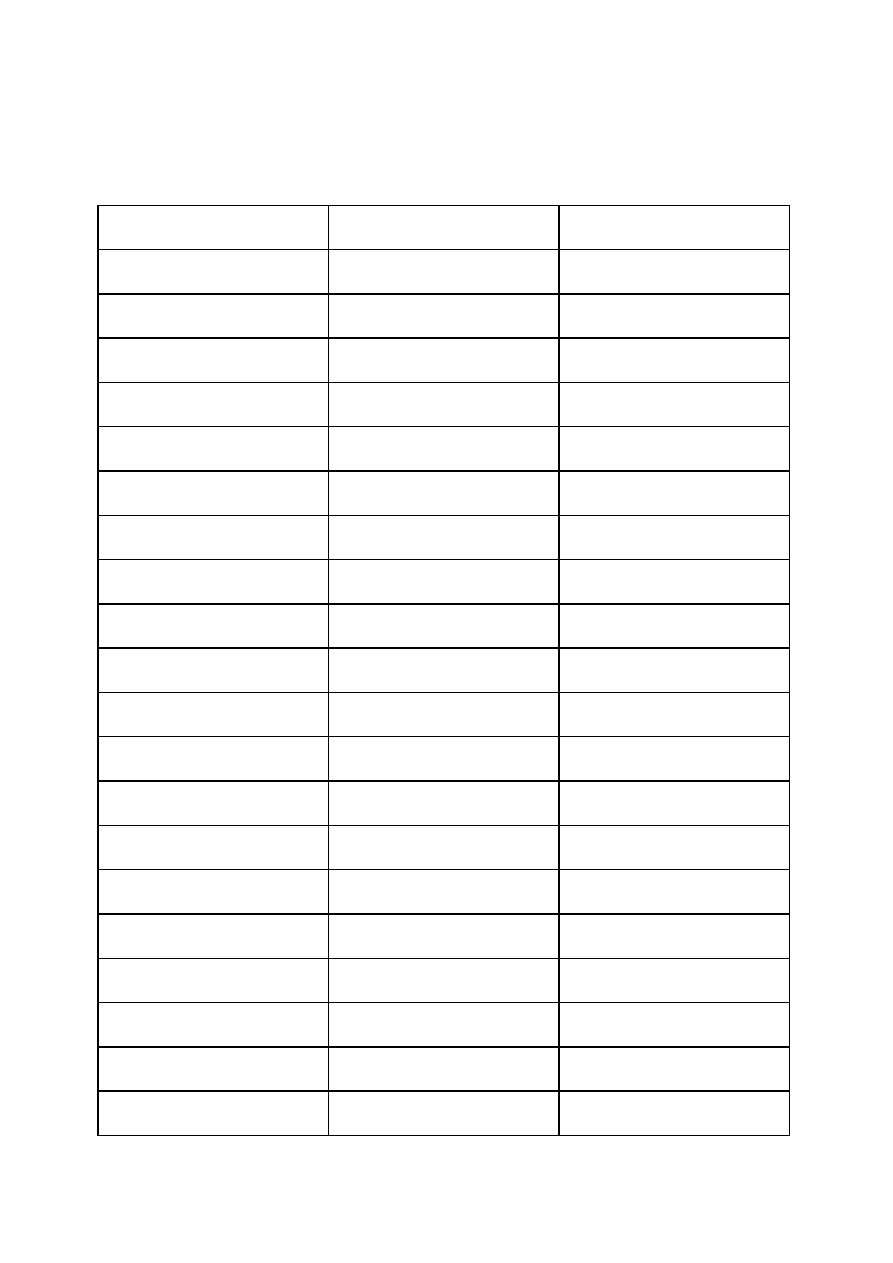
Na podstawie takiego drzewa możemy stworzyć 16 macierzy o rozmiarze 2x2.
W każdej macierzy wybrano punkt siodłowy (zaznaczony pogrubieniem),
wszystkie punkty siodłowe utworzyły nowe drzewo decyzji:

D1/D2

M

S

M

12

5

S

14

8

D1/D2

M

S

M

14

10

S

6

-8

D1/D2

M

S

M

6

13

S

5

-10

D1/D2

M

S

M

-2

0

S

4

16

D1/D2

M

S

M

12

15

S

24

18

D1/D2

M

S

M

4

-15

S

12

6

D1/D2

M

S

M

0

14

S

-8

-2

D1/D2

M

S

M

4

-1

S

-8

-6

D1/D2

M

S

M

-10

-1

S

4

6

D1/D2

M

S

M

6

7

S

14

12

D1/D2

M

S

M

15

19

S

22

24

D1/D2

M

S

M

9

5

S

11

17

D1/D2

M

S

M

15

18

S

-8

12

D1/D2

M

S

M

6

-15

S

9

14

D1/D2

M

S

M

28

26

S

24

15

D1/D2

M

S

M

15

7

S

19

23

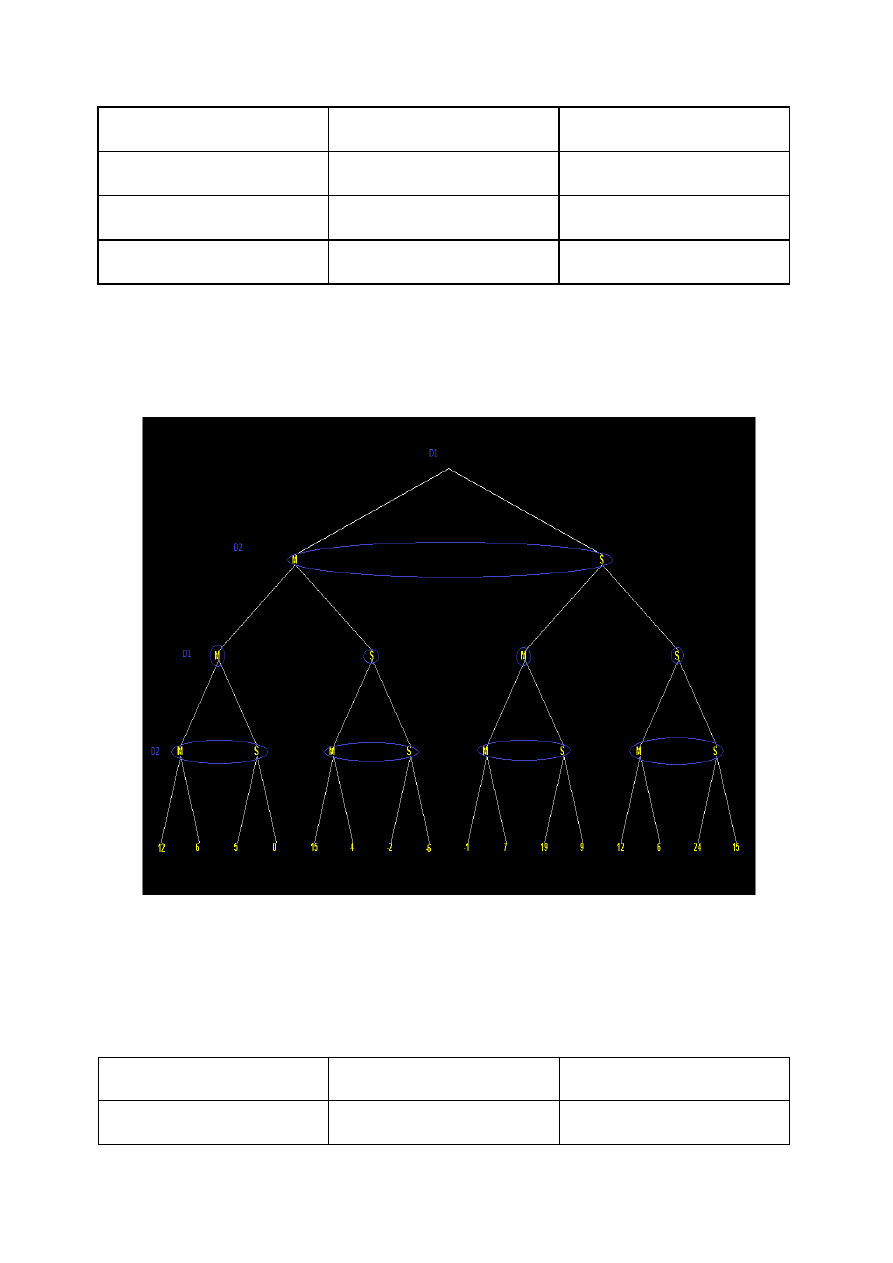
Nowe drzewo:

Po otrzymaniu takiego drzewa stanu, podobnie jak poprzednio tworzymy
macierze 2x2, tym razem będą 4 takie macierze i znów szukamy punktów
siodłowych.

D1/D2

M

S

M

12

5

S

5

0

D1/D2

M

S

M

15

4

S

-2

-6

D1/D2

M

S

M

-1

7

S

19

9

D1/D2

M

S

M

12

6

S

24

15

Po uzyskaniu kolejnych 4 punktów siodłowych tworzymy kolejne drzewo:

Na tym etapie zostaje utworzona jedna macierz o wymiarach 2x2. Znalezienie
punktu siodłowego tej macierzy jest równoznaczne ze znalezieniem wyniku gry:

D1/D2

M

S

M

5

-2

S

7

12

Oznacza to, że wynikiem gry jest 5, a strategią, która pozwala na uzyskanie tego
wyniku:

Gdzie U

AB

oznacza decyzję podjętą przez gracza B na etapie A.

3. Program obliczający wynik gry oraz rysujący drzewa dla dowolnego

k:

Program główny:

A=[12 5 14 18 14 10 6 -8 6 13 5 -10 -2 0 4 16 12 15 24 18 4 -15 12 6 0 14
-8 -2 4 -1 -8 -6 -10 -1 4 6 6 7 14 12 15 19 22 24 9 5 11 17 15 18 -8 12 6 -
15 9 14 28 26 24 15 15 7 19 23];
k=3;
wektor_aktualny=A;
dlugosc=length(A);
for j=1:k
dlugosc=dlugosc/4;
a=1;
for i=1:dlugosc

wektor_aktualny(i)=licz_siodlowe(wektor_aktualny(a),wektor_aktualny(a
+1),wektor_aktualny(a+2),wektor_aktualny(a+3)) ;
a=a+4 ;

end
t = ntree(2,(k-j+1)*2);
plot(t);
end
wynik=wektor_aktualny(1)

licz_siodlowe:
function result = licz_siodlowe(A,B,C,D)
if (A>B && A<C && A<D)
result=A;
elseif (A<B && B<C && B<D)
result=B;
elseif (C>D && C<A && C<B)
result=C;
elseif (C<D && D<A && D<B)
result=D;
end
end