Układy cyfrowe

Sprawozdanie z zajęć laboratoryjnych nr 3

Sprawozdanie z zajęć laboratoryjnych nr 3

1. Układy sekwencyjne

Układami sekwencyjnymi nazywa się układy cyfrowe, w których występują elementy

pamiętające i poprzez to można za ich pomocą realizować bardziej skomplikowane zadania

niż w przypadku układów kombinacyjnych.

W ramach ćwiczenia zapoznaliśmy się z metodą tworzenia liczników zliczających w górę

i w dół z przerzutników JK oraz metodą tworzenia licznika zliczającego do dowolnej

liczby impulsów.

2. Licznik liczący w górę

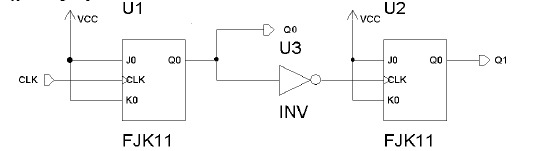
Na rysunku pokazano układ licznika 2 bitowego (rozróżniającego 4 stany), liczącego

wgórę. Zbudowany jest on z dwóch przerzutników JK, do których wejść J i K podane zostały

logiczne sygnały jeden oraz inwertera, którego zadaniem jest odwrócić polaryzację sygnału

wyjściowego z przerzutnika U1.

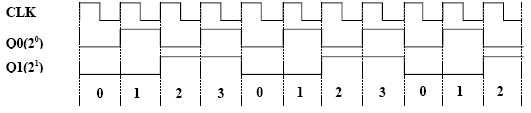
Przyjmując, że sygnał wejściowy CLK jest przebiegiem prostokątnym na wyjściach Q0 i Q1

otrzymujemy następujące przebiegi.

Przypisując wyjściom Q0 i Q1 odpowiednie wagi: Q0 = 20, Q1 = 21, otrzymujemy zapis

binarny liczby kolejnych impulsów zliczonych przez licznik. Liczba możliwych do zliczenia

impulsów wynosi 4, po czym licznik „przekręca się” i zaczyna zliczanie od 0 (licznik modulo

w w w . c h o m i k u j . p l / M a r W a g 9 8 7

Układy cyfrowe

Sprawozdanie z zajęć laboratoryjnych nr 3

4). Inwerter (poprzez swoje własności odwracające) jest w tym układzie elementem

odpowiedzialnym za zmianę zapisu binarnego liczby impulsów w kierunku zliczania w górę.

W celu zwiększania rozmiaru licznika należy rozbudować układ dołączając kolejne

przerzutniki JK do wyjść poprzednich poprzez inwertery. Kolejnym wyjściom z

przerzutników należy nadać wagi kolejnych potęg liczby 2. Możliwe jest uzyskanie liczników

zliczających 2n impulsów wejściowych, przy ilości przerzutników równej n.

3. Licznik liczący w dół

W niektórych przypadkach istnieje potrzeba zastosowania liczników, które zliczają

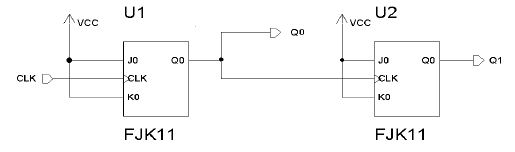
impulsy wejściowe w kierunku malejącym (zliczanie w dół). Na rysunku pokazano układ

takiego licznika binarnego 2 bitowego. Zbudowany jest on, podobnie jak poprzedni, z dwóch

przerzutników JK, jednak w tym przypadku w strukturze nie występuje inwerter.

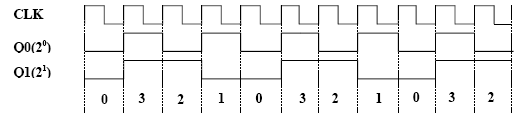
Przyjmując, że sygnał wejściowy CLK jest przebiegiem prostokątnym, na wyjściach Q0 i Q1

otrzymujemy następujące przebiegi.

Ponownie, jeśli przypiszemy wyjściom Q0 i Q1 odpowiednie wagi: Q0 = 20, Q1 = 21, to

otrzymamy zapis binarny liczby kolejnych impulsów zliczonych przez licznik, jednak w tym

przypadku licznik zlicza w dół (od cyfry 3 do cyfry 0). Liczba możliwych do zliczenia

impulsów wynosi 4, po czym licznik „przekręca się”. W celu zwiększania rozmiaru licznika

należy zwiększyć liczbę przerzutników JK dołączając kolejne przerzutniki do wyjść

poprzednich. Kolejnym wyjściom przerzutników należy nadać wagi kolejnych potęg liczby 2.

Możliwe jest uzyskanie liczników zliczających 2n impulsów wejściowych, przy ilości

przerzutników równej n.

w w w . c h o m i k u j . p l / M a r W a g 9 8 7

Układy cyfrowe

Sprawozdanie z zajęć laboratoryjnych nr 3

4. Realizacja licznika binarnego zliczającego zadaną liczbę

impulsów

Wszystkie opisane powyżej liczniki posiadają wejście CD pozwalające na natychmiastowe

skasowanie zawartości licznika. Wejście to może być wykorzystane do ograniczenia liczby

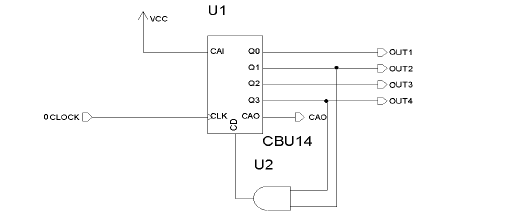
zliczanych w liczniku impulsów. Przykładowo na rysunku poniżej przedstawiono układ

oparty o licznik 4-bitowy, zliczający w górę CBU14, pozwalający na realizację licznika

modulo 10 (zliczającego 10 impulsów o numerach 0 – 9). Układ taki może mieć zastosowanie

jako licznik dziesiętny.

W celu realizacji układu zliczającego do 10 impulsów wejściowych (cyfry od 0 do 9) należy

w oparciu o sygnał wyjściowy z licznika detektować liczbę 10 (jedynki na wyjściach: Q1 -

waga 21 i Q3 – waga 23). Do wykrywania tego stanu służy w tym przypadku bramka AND.

Sygnał wyjściowy z bramki podawany jest na wejście kasowania asynchronicznego i

powoduje natychmiastowe skasowanie licznika i rozpoczęcie zliczania od liczby 0. Dzięki

temu największą wartością mogącą się pojawić na wyjściu licznika jest cyfra 9.

w w w . c h o m i k u j . p l / M a r W a g 9 8 7