Politechnika Świętokrzyska

Metody obliczeniowe

A143.

Grupa: 3ID12B

Piotr Chebdowski

1. Teoria

Metoda najmniejszych kwadratów – standardowa metoda przybliżania rozwiązao układów
nadokreślonych, tzn. zestawu równao, w którym jest ich więcej niż zmiennych. Nazwa „najmniejsze
kwadraty” oznacza, że koocowe rozwiązanie tą metodą minimalizuje sumę kwadratów błędów przy
rozwiązywaniu każdego z równao.

W statystyce wykorzystuje się ją do estymacji i wyznaczania linii trendu na podstawie zbioru danych
w postaci par liczb. Najczęściej jest stosowana przy regresji liniowej, ale może też byd stosowana do
statystycznego wyznaczania parametrów nieliniowych linii trendu.

Regresja liniowa
Żądamy minimalizacji funkcji χ2, która mierzy odchylenie zadanej zależności funkcyjnej od punktów
doświadczalnych. W przypadku funkcji liniowej f(x) = ax + b, funkcja χ2 sprowadza się do

gdzie σ

i

to odchylenie standardowe (niepewnośd pomiaru) danego punktu pomiarowego (w zmiennej

y); czasami używa się notacji Aby znaleźd minima tej funkcji ze względu na parametry a i b,
różniczkuje się po a i b i przyrównuje do 0:

Można te warunki przepisad w wygodniejszej do liczenia postaci, wprowadzając następujące
wielkości

Równania powyższe przepisane w nowych zmiennych po uporządkowaniu mają postad

aS

x

+ bS = S

y

,

aS

xx

+ bS

x

= S

xy

.

Rozwiązaniem tego układu równao liniowych jest

W celu obliczenia niepewności uzyskanych wartości współczynników a i b, korzysta się ze wzoru na
błąd pośredni (różniczka zupełna) funkcji zależnej od parametrów f(yi) (a(yi),b(yi)), przyjmując, że
niepewnośd pomiarowa wynika tylko z niepewności zmiennej y.

Po zastosowaniu tego wzoru do współczynników a i b (czyli obliczeniu pochodnych, podniesieniu do
kwadratu) uzyskuje się wzór na niepewności

Gdzie to odchylenie standardowe zmiennej y (dla jednego pomiaru), które może byd oszacowane na
podstawie odchyleo punktów od prostej.

Przypadek klasyczny
Gdy odchylenie standardowe (niepewnośd pomiaru) wszystkich punktów pomiarowych jest
jednakowe, regresję nazywa się regresją nieważoną (klasyczną lub pierwszego rodzaju), wówczas
odchylenie standardowe może byd wyłączone przed znak sumowania i upraszcza się we wzorach na
współczynniki a, b i inne parametry regresji.
Przyjmując oznaczenia:

Współczynniki prostej określają wzory:

Odchylenie standardowe dane jest za pomocą wzorów:

gdzie

to suma odchyleo standardowych wszystkich pomiarów określona na podstawie analizy

niepewności pomiarowej lub kwadratów odchyleo punktów od prostej regresji,

lub w postaci sum,

Współczynnik korelacji liniowej Pearsona określa wzór:

Współczynnik, którego wartośd mieści się w zakresie od –1 do 1 włącznie, jest bezwymiarowym
wskaźnikiem odzwierciedlającym stopieo liniowej zależności pomiędzy dwoma zbiorami danych.
Wartości –1 i 1 odpowiadają idealnemu ułożeniu punktów na prostej, 0 oznacza brak korelacji między
zmiennymi.

2. Program

public

class

Aproksymacja {

public

static

void

main(String[] args) {

double

S0 = 0, S1 = 0, S2 = 0, T0 = 0, T1 = 0, a0 = 0, a1 = 0;

double

[][] t =

new

double

[8][2];

t[0][0] = -5.84;

t[0][1] = -0.07;

t[1][0] = -5.3;

t[1][1] = -0.11;

t[2][0] = -4.76;

t[2][1] = -0.13;

t[3][0] = -4.22;

t[3][1] = -0.16;

t[4][0] = -3.68;

t[4][1] = -0.19;

t[5][0] = -3.14;

t[5][1] = -0.26;

t[6][0] = -2.6;

t[6][1] = -0.39;

t[7][0] = -2.06;

t[7][1] = -0.81;

S0 = t.

length

;

for

(

int

i = 0; i < t.

length

; i++) {

S1 += t[i][0];

S2 += Math.pow(t[i][0], 2);

T0 += t[i][1];

T1 += t[i][0] * t[i][1];

}

System.

out

.printf(

"S0: %f, S1:%f, S2:%f, T0: %f, T1: %f"

, S0, S1, S2,

T0, T1);

System.

out

.println(

"\nRównania:\nS0*a0 + S1*a1 = T0\nS1*a0 + S2*a1 =

T1"

);

a1 = ((T1 * S0) / (-(S1 * S1) + S0 * S2))

- ((S1 * T0) / (-(S1 * S1) + S0 * S2));

a0 = (T0 / S0) - ((S1 * a1) / S0);

System.

out

.println(

"a0 ="

+ a0 +

", a1 ="

+ a1);

System.

out

.printf(

"f(x) = %f + %f * x"

, a0, a1);

}

}

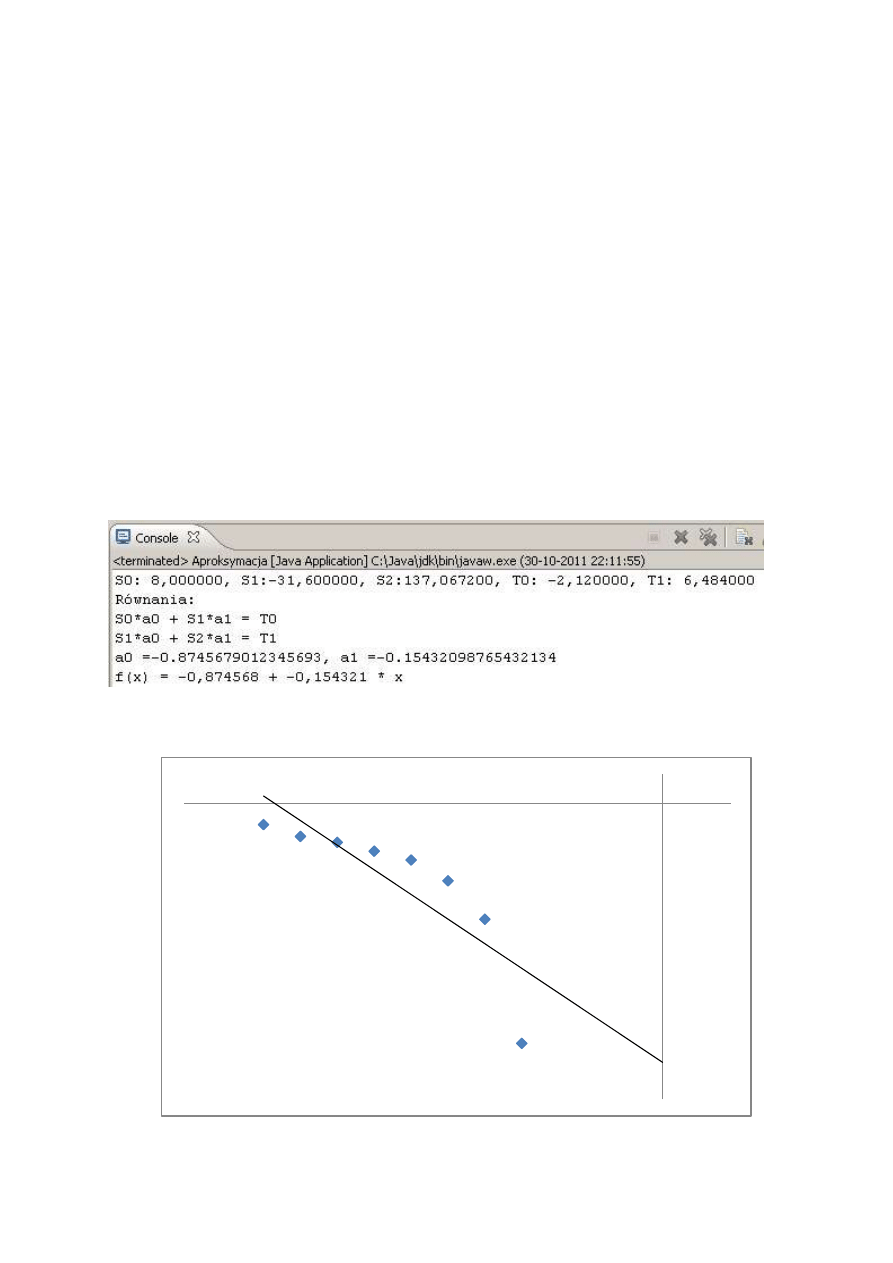
3. Konsola

4. Wykres

-1

-0,9

-0,8

-0,7

-0,6

-0,5

-0,4

-0,3

-0,2

-0,1

0

0,1

-7

-6

-5

-4

-3

-2

-1

0

1