Politechnika Świętokrzyska 

Metody obliczeniowe

 

SCILAB 

Grupa: 312B 

Piotr Chebdowski 

 

1. Dostosowad podane skrypty do wykorzystania w programie SciLab. 

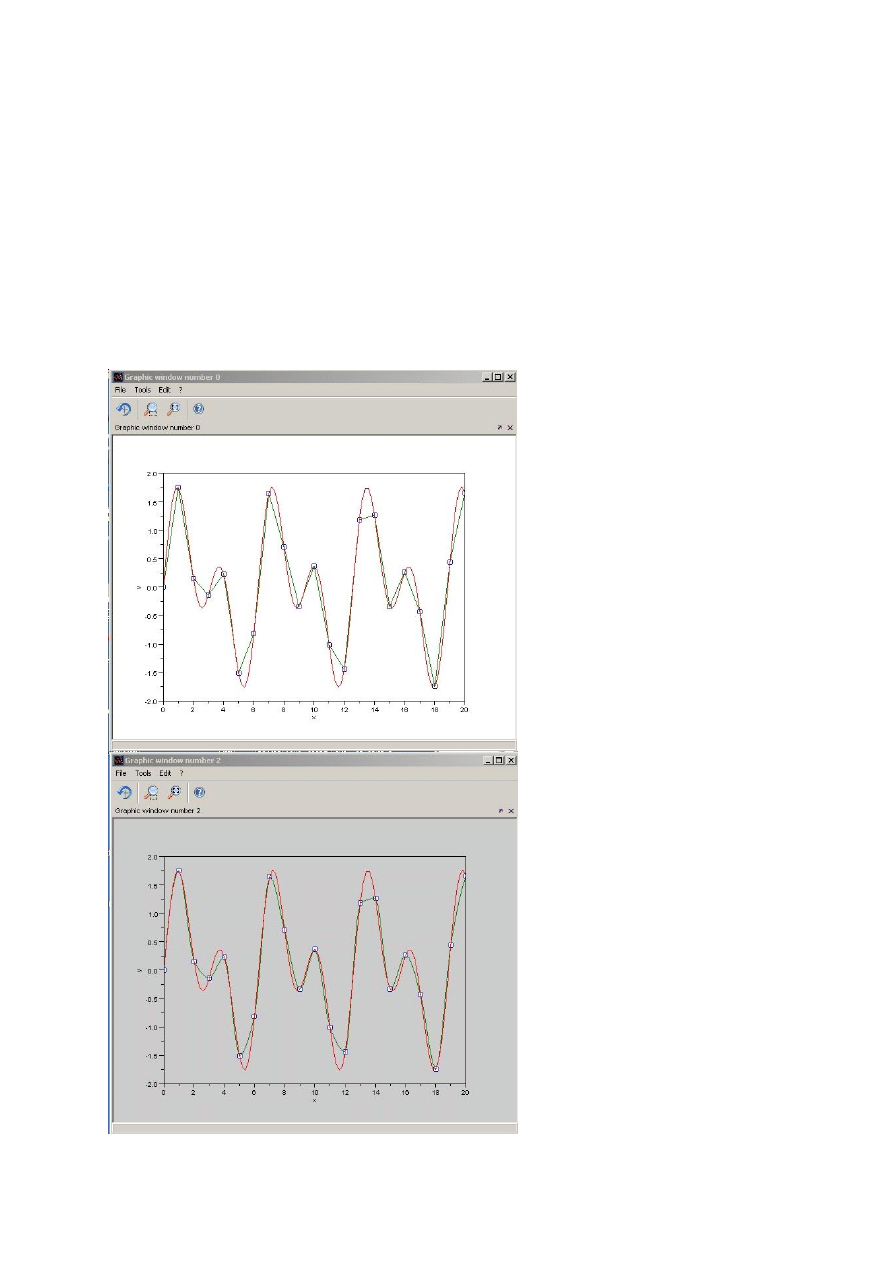
Interpolacja – skrypt 1: 

x=-2:0.05:2; y=x.^2-1; 
i=[1:20:81]; 
x0=x(i); y0=y(i); 
xi=-2:0.1:2; yi=zeros(4,size(xi,2)); 
 
yi(1,:)=interp1(x0,y0,xi,'nearest'); 
yi(2,:)=interp1(x0,y0,xi,'linear'); 
yi(3,:)=interp(xi, x0, y0, splin(x0, y0, 'monotone')); 
yi(4,:)=interp1(x0,y0,xi,'spline'); 
 
tytul = cellstr(['najblizszy sasiad'; 
     'interpolacja liniowa'; 
     'wielomian 3-go rzedu'; 
     'sklejane wielomiany 3-go rzedu']); 
 
 
for i=1:4 
 

subplot(2,2,i) 

 

plot(x,y), set(gca(),"auto_clear","off") 

 

plot(x0,y0,'o') 

 

plot(xi,yi(i,:), '--') 

end 

 

 

 
 
Interpolacja – skrypt 2: 

x = 0:20; 
y = sin(x) + sin(2*x); 

xi = 0:.2:20; 
yi = interp1(x, y, xi, 'linear'); 
plot(x, y, 'o', xi, yi, xi, sin(xi) + sin(2*xi)) 
xlabel('x'); 
ylabel('y'); 
figure(2); 
yi = interp(xi, x, y, splin(x, y, 'monotone')); 
plot(x, y, 'o', xi, yi, xi, sin(xi) + sin(2*xi)); 
xlabel('x'); 
ylabel('y'); 
figure(3); 
yi = interp1(x, y, xi, 'spline'); 
plot(x, y, 'o', xi, yi, xi, sin(xi) + sin(2*xi)); 
xlabel('x'); 
ylabel('y'); 
 

 

 

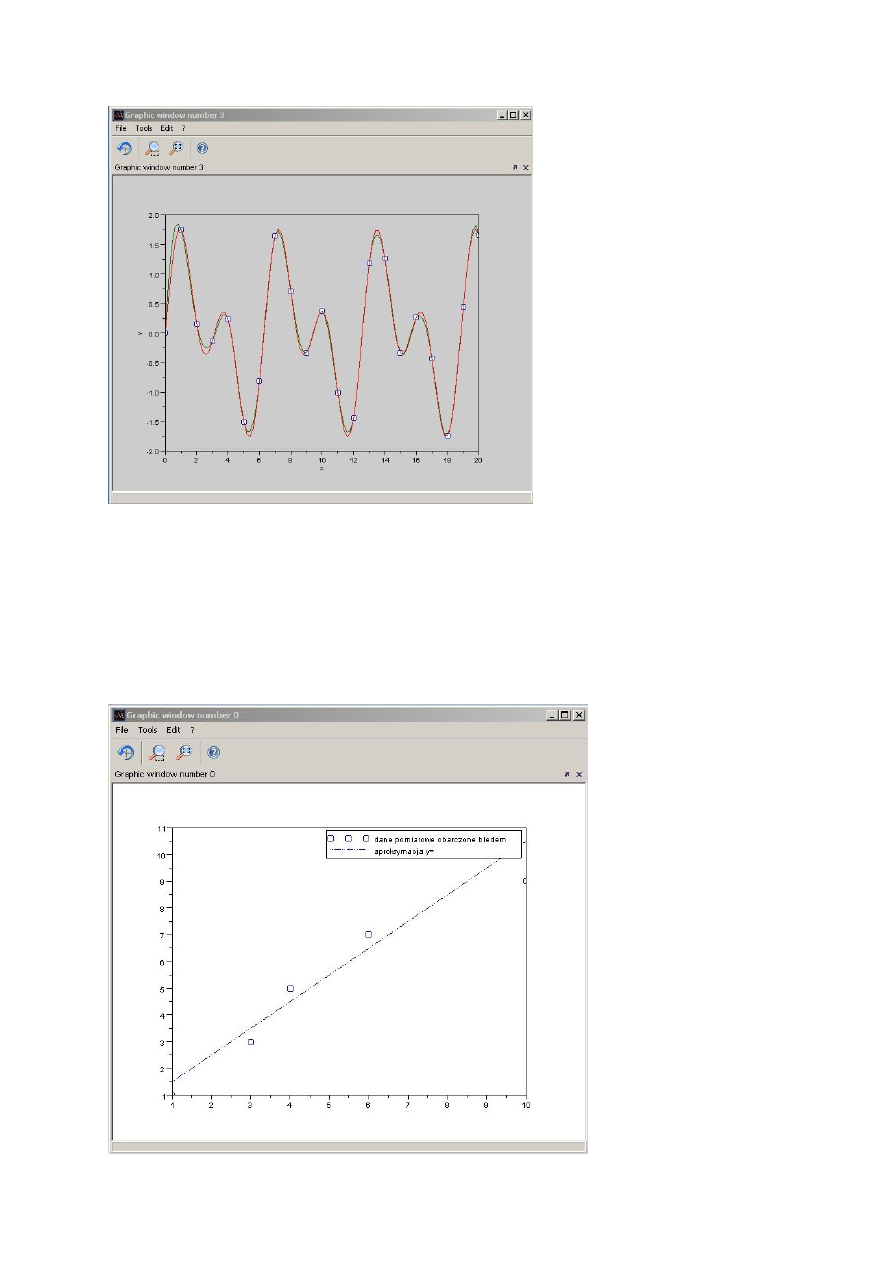
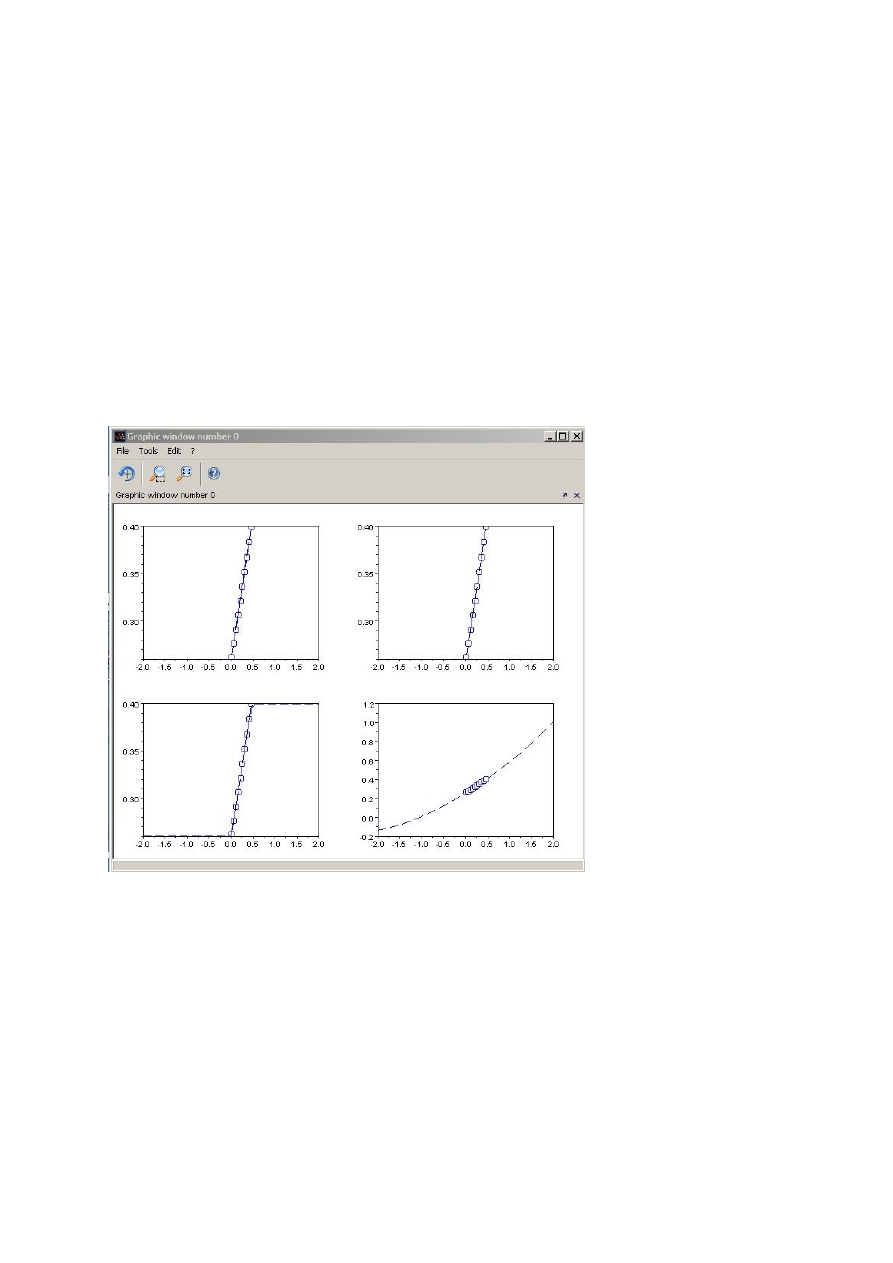
Aproksymacja: 

x=[1 3 4 6 8 10]; 
y=[1 3 5 7 10 9]; 
a=(size(x,2)*sum(x.*y)-sum(x)*sum(y))/(size(x,2)*sum(x.^2)-sum(x)^2); 
b=(sum(y)*sum(x.^2)-sum(x)*sum(x.*y))/(size(x,2)*sum(x.^2)-sum(x)^2); 
xw=[1 10]; 
yw=a*xw+b; 
plot(x,y,'o'), plot(xw,yw,':') 
tekst='aproksymacja y=',msprintf('%4.1f',a),'x',msprintf('%+4.1f',b); 
legend('dane pomiarowe obarczone bledem',tekst) 
 

 

 

2. Dostosowad skrypty do zadao podanych do dwiczeo. 

Interpolacja: 

x=[0.01 0.06 0.11 0.16 0.21 0.26 0.31 0.36 0.41 0.46]; 
y=[0.26183 0.27644 0.29122 0.30617 0.32130 0.33660 0.35207 0.36773 0.38357 0.39959]; 
i=[1:1:10]; 
x0=x(i); y0=y(i); 
xi=-2:0.1:2; yi=zeros(4,size(xi,2)); 
 
yi(1,:)=interp1(x0,y0,xi,'nearest'); 
yi(2,:)=interp1(x0,y0,xi,'linear'); 
yi(3,:)=interp(xi, x0, y0, splin(x0, y0, 'monotone')); 
yi(4,:)=interp1(x0,y0,xi,'spline'); 
 
for i=1:4 
 

subplot(2,2,i) 

 

plot(x,y), set(gca(),"auto_clear","off") 

 

plot(x0,y0,'o') 

 

plot(xi,yi(i,:), '--') 

end 

 

 

 
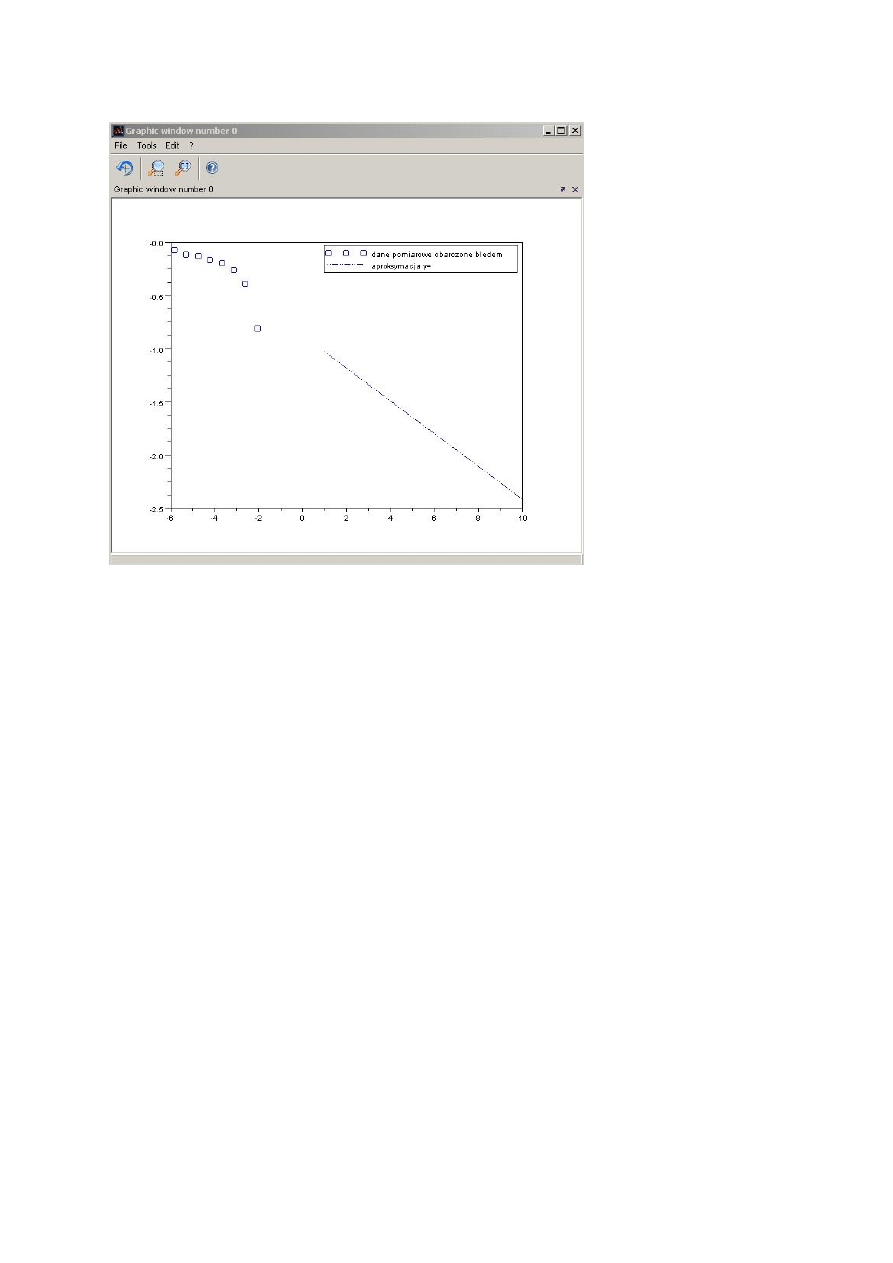
Aproksymacja: 

x=[-5.84 -5.3 -4.76 -4.22 -3.68 -3.14 -2.6 -2.06]; 
y=[-0.07 -0.11 -0.13 -0.16 -0.19 -0.26 -0.39 -0.81]; 
a=(size(x,2)*sum(x.*y)-sum(x)*sum(y))/(size(x,2)*sum(x.^2)-sum(x)^2); 
b=(sum(y)*sum(x.^2)-sum(x)*sum(x.*y))/(size(x,2)*sum(x.^2)-sum(x)^2); 
xw=[1 10]; 
yw=a*xw+b; 
plot(x,y,'o'), plot(xw,yw,':') 
tekst='aproksymacja y=',msprintf('%4.1f',a),'x',msprintf('%+4.1f',b); 
legend('dane pomiarowe obarczone bledem',tekst)