Politechnika Świętokrzyska 

Metody obliczeniowe

 

W27. 

Grupa: 312B 

Piotr Chebdowski 

 

1. Zmodyfikowana metoda Eulera.

 

W  zmodyfikowanej  metodzie  Eulera  wykorzystujemy  dodatkowo  styczną  w  punkcie 
P, będącym środkiem przedziału (t, t+h): 

Najpierw znajdujemy 

styczną w punkcie t, a następnie na jej podstawie wyznaczamy 

wartość  punktu  P  odległego  od  t  o  h/2.  Wartość  szukanej  funkcji  w  punkcie  t+h 
znajdujemy z kolei w oparciu o równanie stycznej w wyznaczonym punkcie P. 

W metodzie tej błąd będzie mniejszy – gdyż w kolejnych krokach analizujemy punkty 
odległe od siebie o h/2 a nie o h. 

Wzór opisujący sposób znajdowania kolejnego punktu można zapisać: 

 

 
Funkcja realizująca zmodyfikowaną metodę Eulera: 

 
 
 

K1, K2 

– wartości pomocnicze 

wzór obliczający kolejne wartości – 
z 

wykorzystaniem wartości 

pomocniczej K2 

 

 

 

 

 
 
 
 
 
 

 
 
 
 
 

y

n 1

y

n

h f t

n

h

2

y

n

h

2

f t

n

y

n

t

 

Euler2 t0 y0 a b h

(

)

y

0

y0

t

0

t0

K1

h f t

i 1

y

i 1

K2

h f t

i 1

h

2

y

i 1

K1

2

y

i

y

i 1

K2

t

i

t

i 1

h

i

1

b

a

h

for

y

t

 
 
 
 
 
 
 
 
 
 

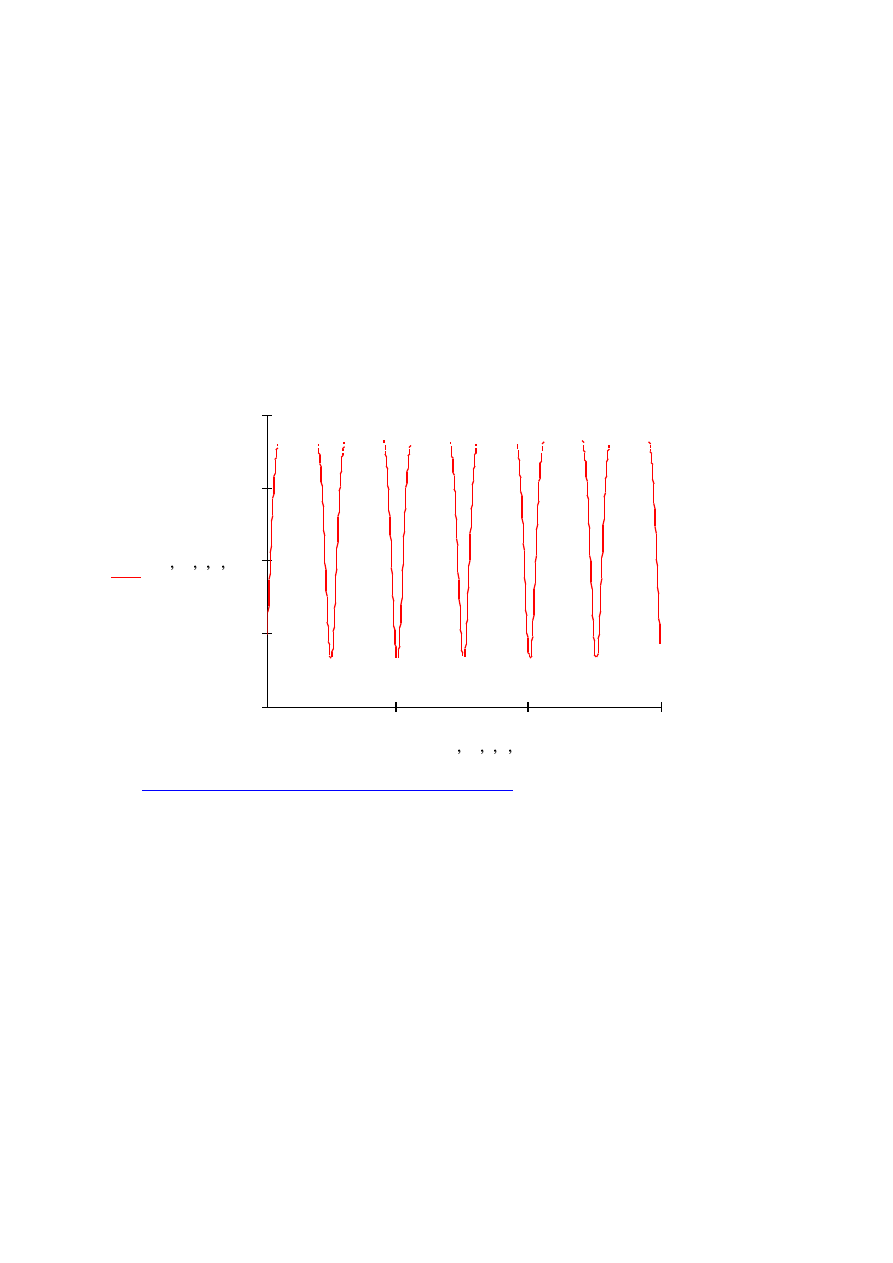
Rozwiązanie  (założenia  i  warunki  początkowe  –  jak  w  podstawowej  metodzie 
Eulera): 

 
 

 

Źródło: 

http://student.agh.edu.pl/~drelek/studia/3semestr/metody/sprawozdanie 4 rr.doc

 

 

 

2. Program. 

public

 

class

 RrrzRK { 

 

private

 Double[] 

y

 = 

new

 Double[11]; 

 

private

 Double[] 

x

 = 

new

 Double[11]; 

 

private

 Double[][] 

k

 = 

new

 Double[11][4]; 

 

private

 Double[][] 

mk

 = 

new

 Double[11][4]; 

 

private

 Double[] 

suma

 = 

new

 Double[11]; 

 

private

 Double 

h

; 

 
 

public

 RrrzRK() { 

 

 

h

 = 0.1; 

 

 

x

[0] = 1.7; 

 

 

y

[0] = 5.6; 

 

} 

 
 

private

 

double

 function(Double x, Double y) { 

 

 

return

 

h

 * (x + Math.cos((y + x) / Math.

PI

)); 

 

} 

 
 

private

 

void

 rK() { 

50

100

150

0.8

1

1.2

1.4

1.6

Euler2 t0 y0 a b h

(

)

0

Euler2 t0 y0 a b h

(

)

1

 

 

for

 (

int

 i = 0; i < 11; i++) { 

 

 

 

suma

[i] = 0.0; 

 

 

 

k

[i][0] = function(

x

[i], 

y

[i]); 

 

 

 

mk

[i][0] = 

k

[i][0]; 

 

 

 

k

[i][1] = function(

x

[i] + 0.5 * 

h

, 

y

[i] + 0.5 * 

k

[i][0]); 

 

 

 

mk

[i][1] = 2 * 

k

[i][1]; 

 

 

 

k

[i][2] = function(

x

[i] + 0.5 * 

h

, 

y

[i] + 0.5 * 

k

[i][1]); 

 

 

 

mk

[i][2] = 2 * 

k

[i][2]; 

 

 

 

k

[i][3] = function(

x

[i] + 

h

, 

y

[i] + 

k

[i][2]); 

 

 

 

mk

[i][3] = 

k

[i][3]; 

 

 

 

suma

[i] = (

mk

[i][0] + 

mk

[i][1] + 

mk

[i][2] + 

mk

[i][3]) / 6; 

 

 

 

if

 (i < 10) { 

 

 

 

 

x

[i + 1] = 

x

[i] + 

h

; 

 

 

 

 

y

[i + 1] = 

y

[i] + 

suma

[i]; 

 

 

 

} 

 

 

 

System.

out

.printf(

"y = %f   dla x = %.1f\n"

, 

y

[i], 

x

[i]); 

 

 

} 

 

} 

 
 

public

 

static

 

void

 main(String[] args) { 

 

 

RrrzRK r = 

new

 RrrzRK(); 

 

 

r.rK(); 

 

} 

} 

 

 

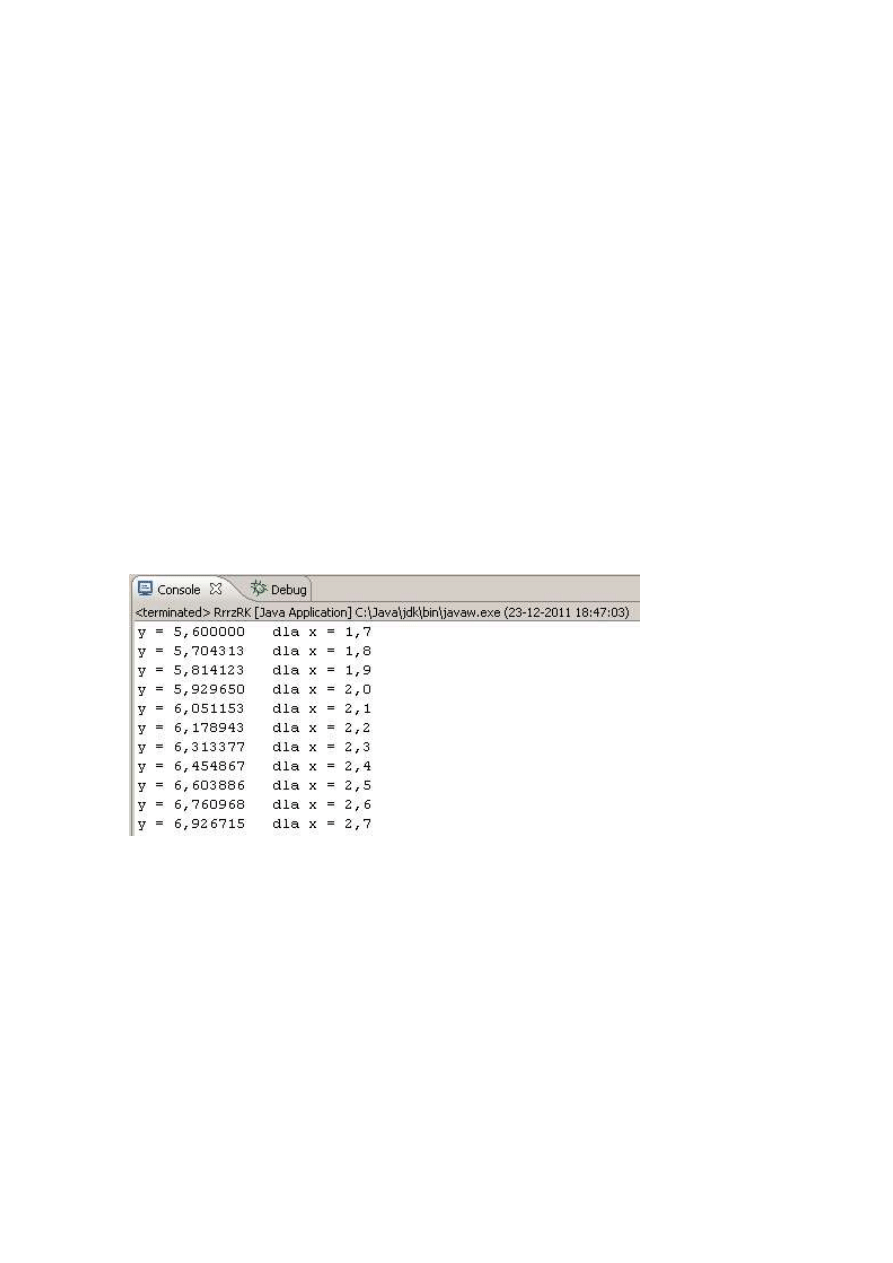
3. Konsola.