LABORATORIUM  

9

WERYFIKACJA HIPOTEZ 

STATYSTYCZNYCH

PARAMETRYCZNE TESTY 

ISTOTNOŚCI

1.Test dla dwóch średnich 

P.G.

2.Testy dla wskaźnika 

struktury

3.Testy dla wariancji

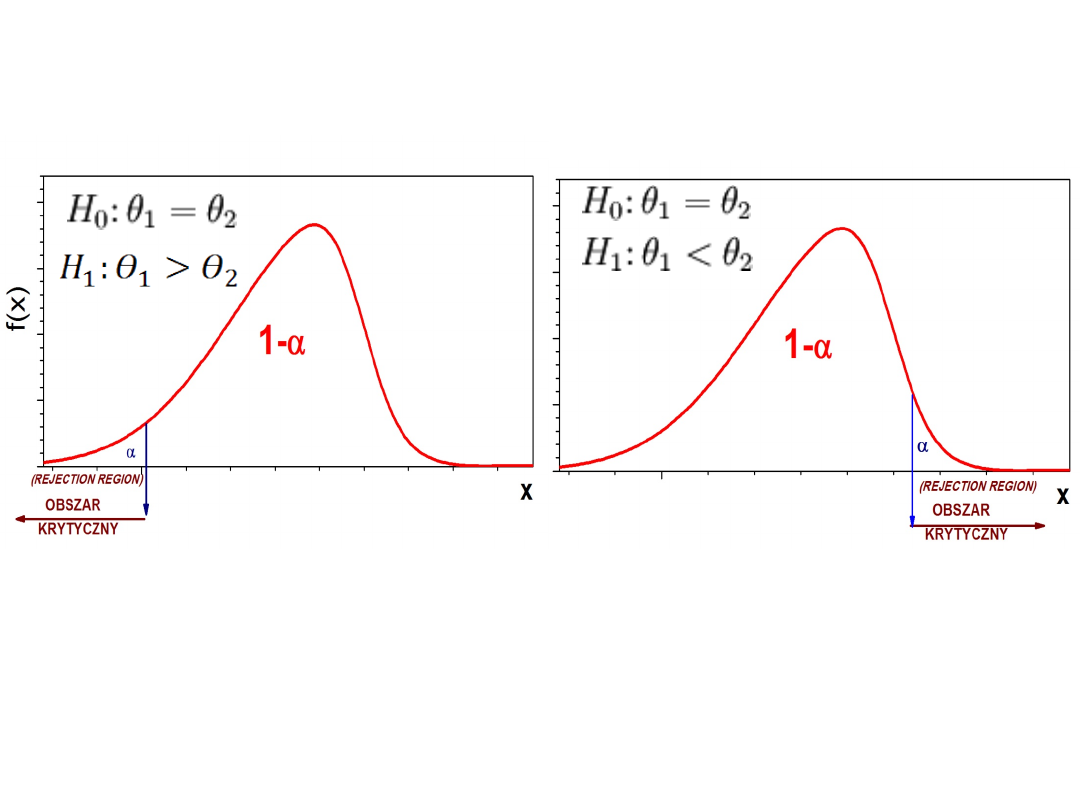
OBSZAR KRYTYCZNY

LEWOSTRONNY 

OBSZAR 

KRYTYCZNY

Test jednośladowy

(one- tail test)

PRAWOSTRONNY 

OBSZAR 

KRYTYCZNY

Test jednośladowy

(one- tail test)

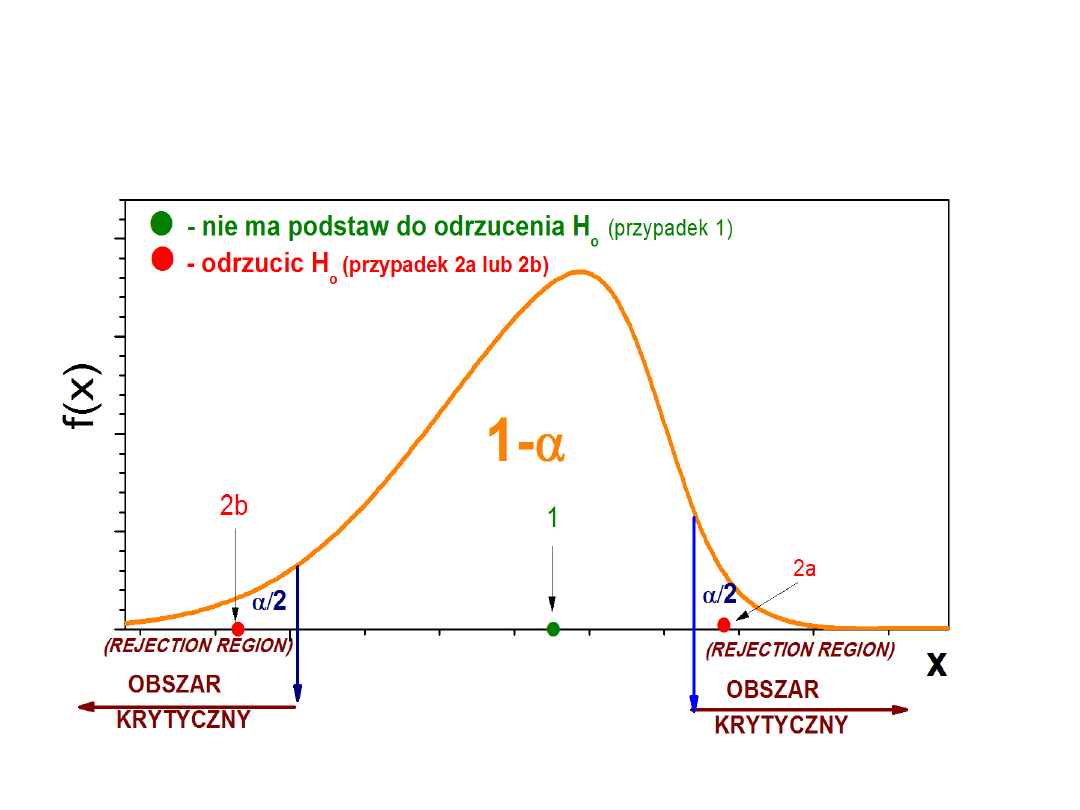
DECYZJE

Obszar krytyczny od pozostałej części rozkładu statystyki oddzielony jest przez tzw. wartości 
krytyczne testu czyli wartości odczytane z rozkładu statystyki przy danym α, tak aby spełniona 
była relacja zależna od sposobu sformułowania H

1

.

TEST DLA WSKAŹNIKA STRUKTURY 

(PROCENTU)

Populacja generalna ma rozkład dwupunktowy z 
parametrem p . Z populacji tej wylosowano  próbę n-
elementową  (n>100) próbę. W oparciu o wynik tej 
próby zweryfikować hipotezę: 

H

o 

 :  p=p

o

  

wobec  

hipotezy alternatywnej: 

H

1 

: p p

o

 

, gdzie p

o

 jest 

hipotetyczna wartość parametru p

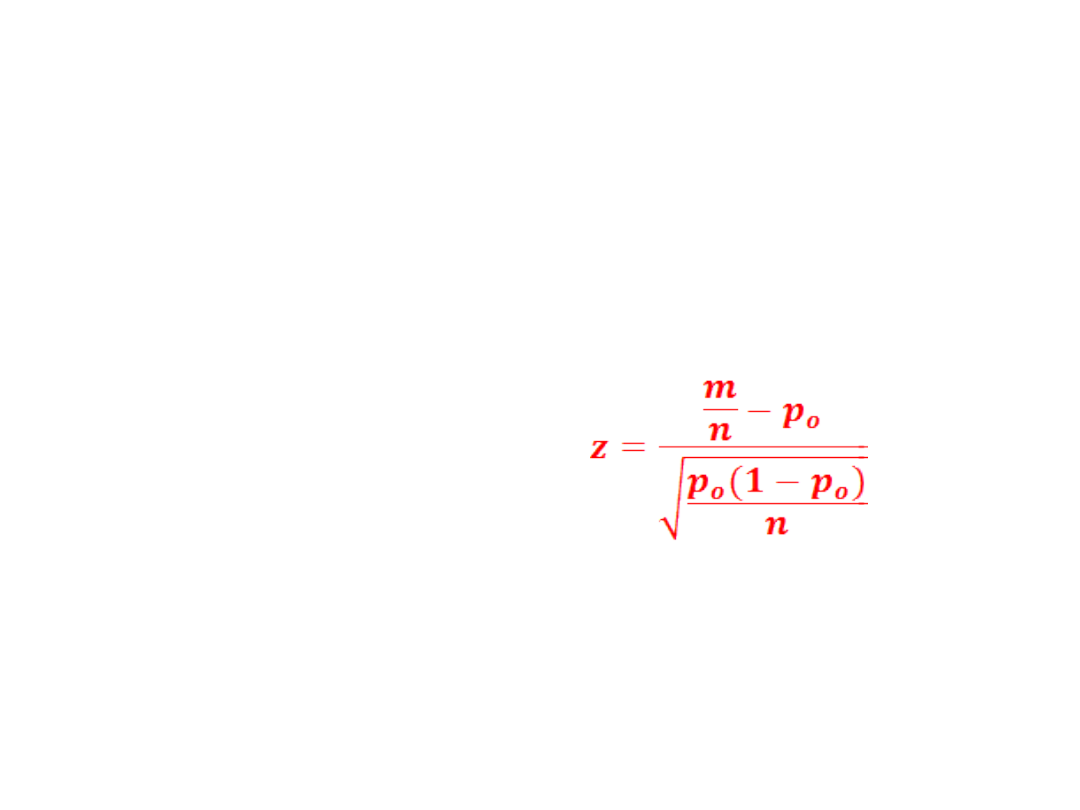
Statystyka testowa:

Gdzie m- liczba wyróżnionych elementów w 
próbie. Statystyka z ma rozkład N(0,1) 

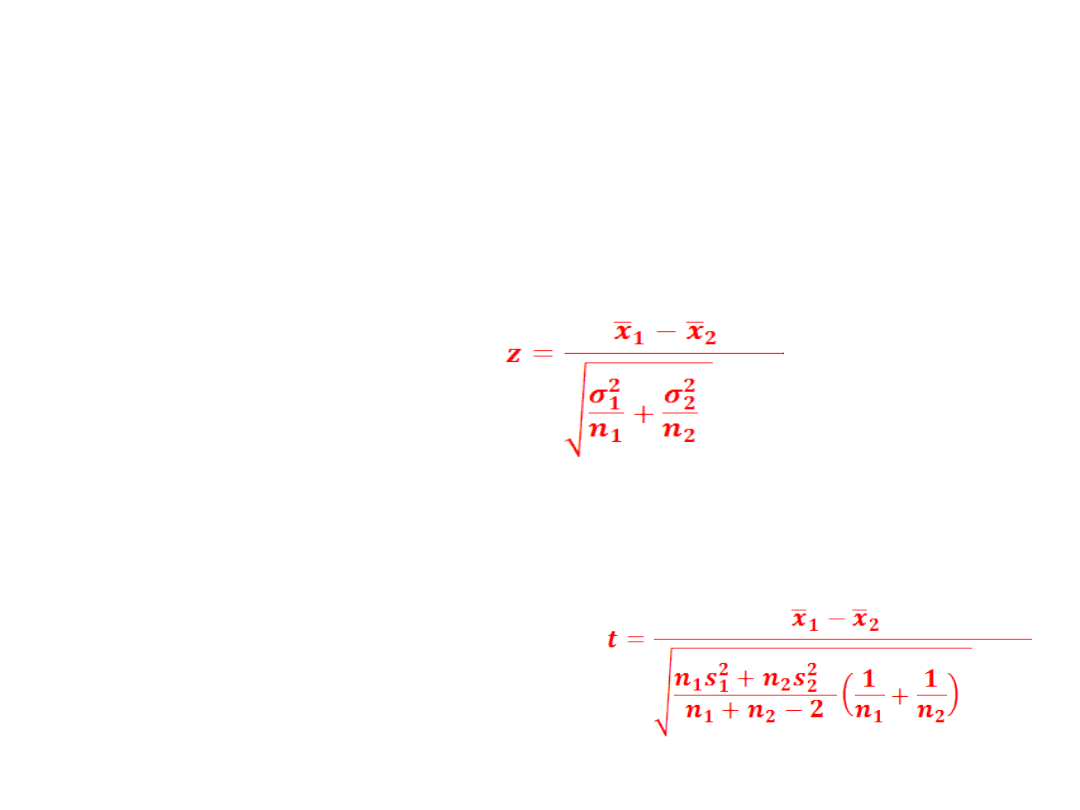
TESTY DLA DWÓCH ŚREDNICH 

POPULACJI

Przypadek 1.
Dwie populacje generalne o rozkładach normalnych N(µ

1

, σ

1

)  i 

N(µ

2

, σ

2

) . Odchylenia standardowe σ

1

 i σ

2

  są znane. W oparciu o 

wyniki dwu niezależnych prób, o liczebnościach n

1  

i  n

2  

wylosowanych z tych populacji  sprawdzić hipotezę: 

H

o 

 : µ

1

  = µ

2 

, 

wobec hipotezy alternatywnej:     

H

1 

 : µ

1

  µ

2 

Rozwiązanie:  Statystyka testowa:                                               
ma rozkład  N(0,1)

Rozwiązanie:  Statystyka testowa: 

Przypadek 2

.

Dwie populacje generalne o rozkładach normalnych N(µ

1

, σ

1

) i 

N(µ

2

, σ

2

) Odchylenia standardowe σ

1

 i σ

2

  są nieznane, ale 

jednakowe: σ

1

 = σ

2

. W oparciu o wyniki dwu niezależnych prób, o 

liczebnościach n

1  

i  n

2  

wylosowanych z tych populacji  sprawdzić 

hipotezą: 

H

o 

 : µ

1

  = µ

2 

, 

wobec hipotezy alternatywnej: 

H

1 

 : µ

1

  µ

2 

ma rozkład t-Studenta o k= n

1

 + n

2 

-2   stopniach swobody.

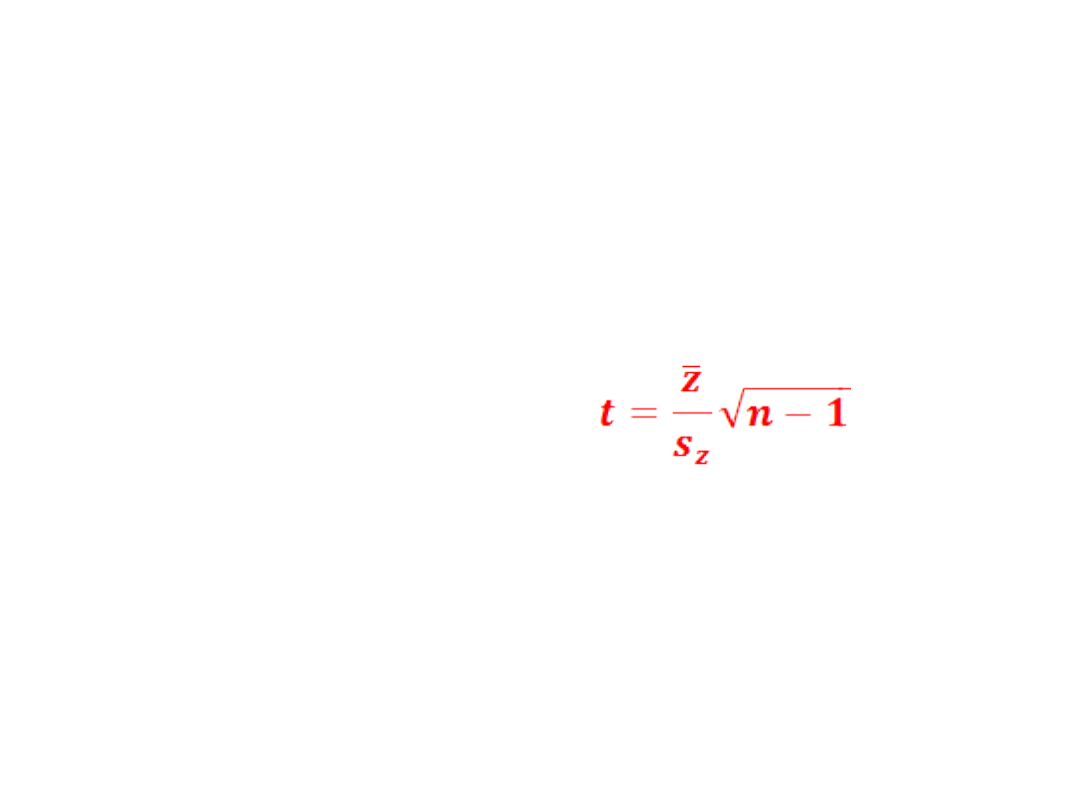
TESTY DLA DWÓCH ŚREDNICH 

POPULACJI

Uwaga: Często   zdarza się, że  wyniki obu prób możemy 
traktować  jako wyniki pomiarów na tych samych 
elementach. Typową sytuacją jest przypadek: wynik x

i

 

‘przed’ jakąś operacją i wynik y

i

 ‘po’ niej dla tego

 samego ‘i’ . Można wtedy analizować wyniki obu prób jako 
wyniki jednej próby różnicowej 

z

i 

= y

i

- x

i. 

Wówczas 

testujemy hipotezę: 

H

o

:  µ

z

=0 

, gdzie 

µ

z  

ś

rednia w populacji 

różnic. 

Statystyka testowa:

ma  rozkład t-Studenta o 
k=n-1.

Przypadek 3.
Dwie populacje generalne o rozkładach normalnych  lub innych. 
Odchylenia standardowe σ

1

 i σ

2

  są nieznane. W oparciu o wyniki 

dwu niezależnych dużych prób, o liczebnościach n

1  

i  n

2  

wylosowanych z tych populacji  sprawdzić hipotezę: 

H

o 

 : µ

1

  = µ

2 

, 

wobec hipotezy alternatywnej: 

H

1 

 : µ

1

  µ

2 

Rozwiązanie: Postępujemy tak samo, jak w Przypadku 1, z tym 
że przy obliczaniu wartości  statystyki testowej w miejsce σ

1

 i σ

2

  

wstawiamy :

s

1

 i  s

2

TEST DLA DWÓCH WSKAŹNIKÓW 

STRUKTURY

Dwie populacje generalne o rozkładach dwupunktowych 
z parametrami p

1

 i p

2

 . W oparciu o wyniki dwu 

niezależnych prób, o liczebnościach n

1  

i  n

2 

 (n

1 

>100 i 

n

2 

>100) wylosowanych z tych populacji  sprawdzić 

hipotezę, że parametry p

1

 i p

2  

są  jednakowe, tzn: 

H

o 

 :  

p

1

 =p

2  

wobec  hipotezy alternatywnej: 

H

1 

: p

1

   p

2

 .

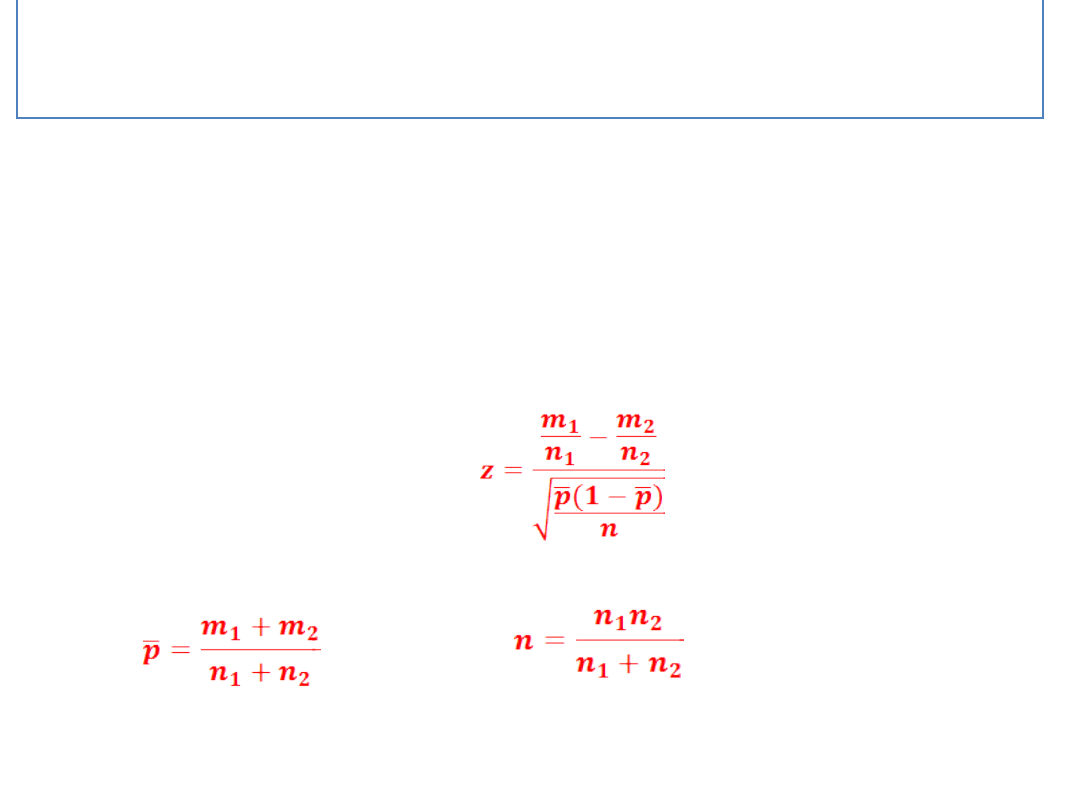
Statystyka testowa:

gdzie:  m

1 

i  m

2 

 oznaczają ilość wyróżnionych elementów w obu 

próbach, a

: 

z- ma  rozkład 
N(0,1) 

TEST DLA WARIANCJI 

POPULACJI

Populacja generalna ma rozkład normalny N(µ, σ) o nieznanych 
parametrach µ  i σ.  Z populacji tej wylosowano  próbę n-
elementową próbę, na jej podstawie sprawdzić hipotezę:  

H

o 

:           

           wobec hipotezy alternatywnej:

H

1

 :                      , 

gdzie       

 jest hipotetyczną wartością wariancji

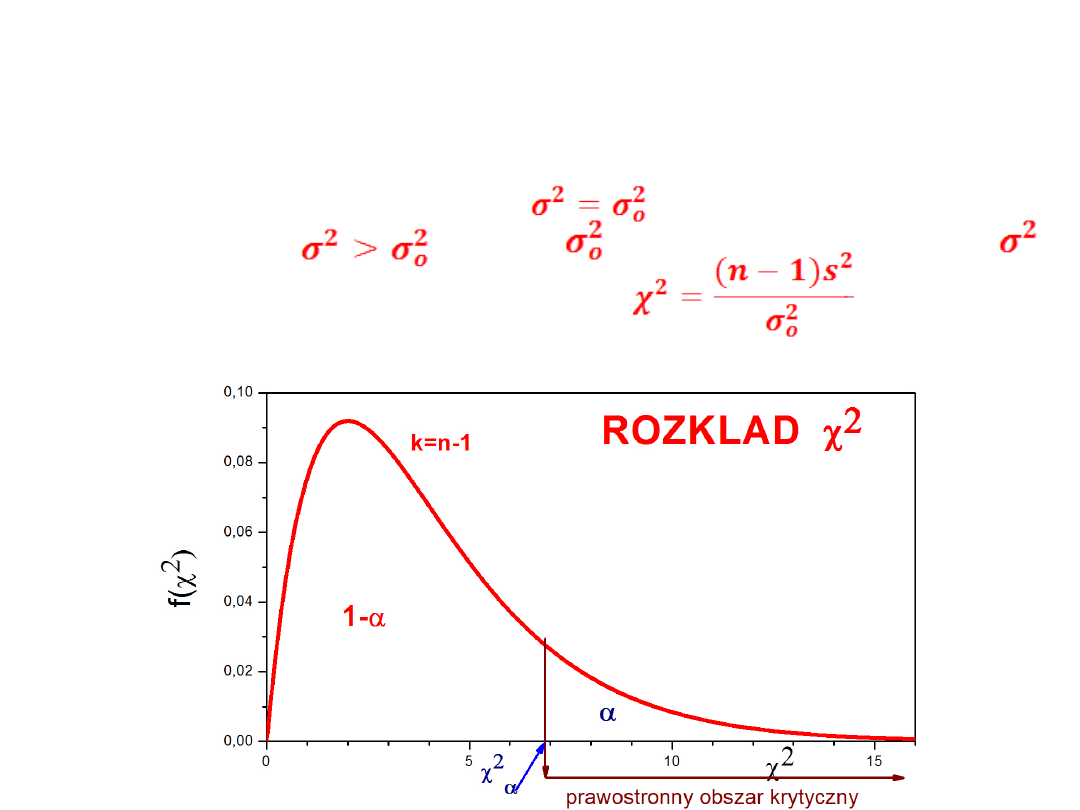
Rozwiązanie:  Statystyka testowa: 

Statystyka ta ma rozkład χ

2

 z k=n-1  stopniami 

swobody 

TEST DLA DWÓCH WARIANCJI POPULACJI

Dane są dwie populacje generalne o rozkładach normalnych 
N(µ

1

, σ

1

)  i N(µ

2

, σ

2

) . Ich parametry są nieznane. W oparciu o 

wyniki dwu niezależnych prób, o liczebnościach n

1  

i  n

2  

wylosowanych z tych populacji  sprawdzić hipotezę:  

H

o

:

          

            wobec hipotezy alternatywnej: 

H

1

:

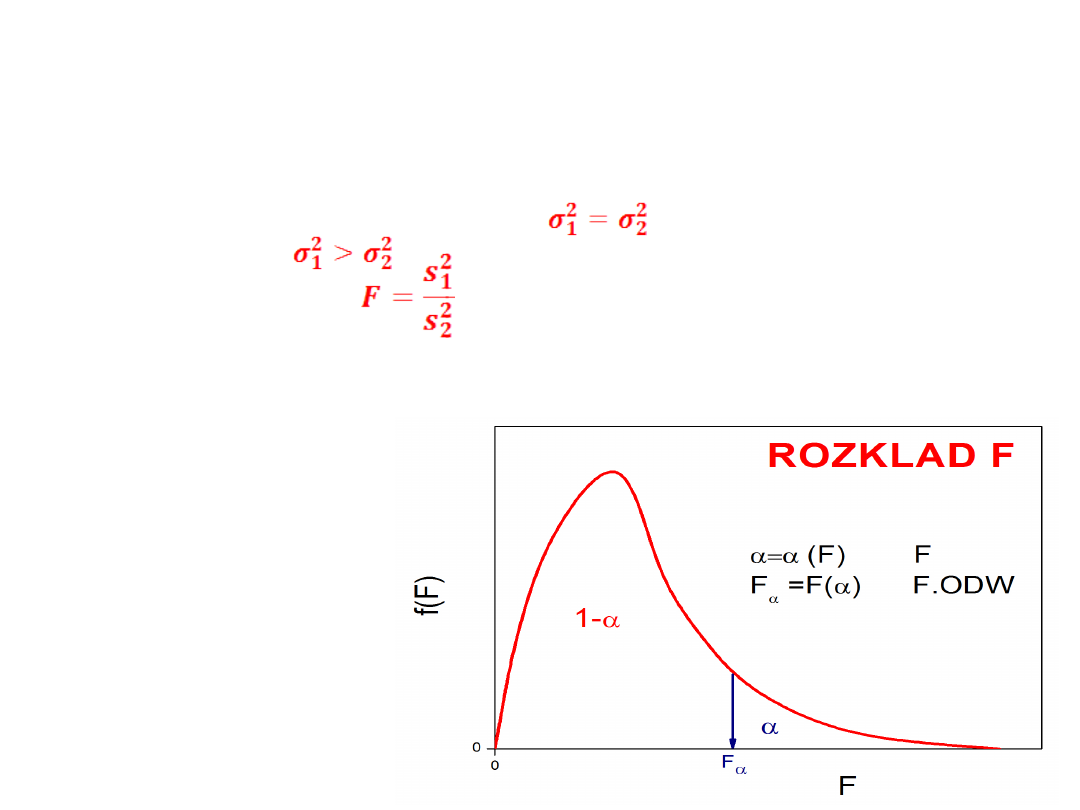
Statystyka testowa

:                         ma rozkład F-Snedecora z 

k

1

=n

1

-1 oraz  

k

2

 =n

2

 -1 stopniami swobody.                                  

Gdy  

F  

F



 

odrzucamy H

o

 

ĆWICZENIA

1. Spośród studentów AGH wylosowano niezależnie do próby 200 

studentów i zapytano ich czy palą i ile dziennie palą 
papierosów. 152 studentów z nich stwierdziło, ze pali 
systematycznie, a wariancja z tej próby wypalanych 
papierosów wynosi s

2

=50 (papierosów)

2

. Na poziomie 

istotności α=0,05 zweryfikować hipotezy:

a) palących studentów na AGH jest 60 %,
b) odchylenie standardowe liczby wypalanych dziennie 

papierosów wynosi 5. 

5G.p.87, z. 2.62, p. 78 z. 2.46 

2. Wykonano pomiary  porowatości 8-miu  wylosowanych 

kształtek ceramicznych przed i po modyfikacji polegającej na 
dodatkowym procesie spiekania, uzyskano następujace wyniki 
porowatości w [%]:

     przed modyfikacją: 21, 17, 20,  26,  23,  22,  21 , 18
           po modyfikacji: 16, 13, 14,  21,  19,  18,  26,   17 
     Na poziomie istotności  α=0,05   zweryfikować hipotezę, że 

modyfikacja zmniejsza porowatość tych wyrobów.  Zastosować 
test dla par na różnicach wyników. 

(G.p.70 z. 2.23)