Metody i narzędzia informatycznego wspomagania decyzji - projekt przejściowy Środowisko

optymalizacyjne

GAMS 2.0

Literatura

GAMS20.0\docs\gams\Tutorial.pdf

Biblioteka przykładów (GAMS Model Library)

www.gams.com

Problem (1) Fabryka produkuje napoje gazowane w trzech różnych opakowaniach – szklanym, plastikowym oraz puszkach.

Przy produkcji każdego z opakowań wykorzystywane są kolejno trzy rodzaje maszyn. Maksymalny czas pracy tych maszyn w ciągu miesiąca jest następujący - 150 godzin dla maszyn I rodzaju, 160 godzin dla maszyny II rodzaju oraz 170 godz dla maszyny II rodzaju.

Problem (2) Czas pracy poszczególnych maszyn na jedną sztukę każdego z opakowań dany jest w następującym zestawieniu:

pusz

plast

szk

ło

k

ik

a

maszyna A

2

1

1

maszyna B

1

1

2

maszyna C

1

2

1

Problem (3) Jednostkowe zyski z zastosowania poszczególnych rodzajów opakowań są następujące:

Zysk

Jak należy zaplanować produkcję by odnieść jak największy zysk, przy puszka

3

założeniu że popyt jest wystarczająco duży niezależnie od rodzaju plastik

7

opakowania?

szkło

5

Analiza problemu – zapis formalny Dla macierzy pracochłonności: 2 1 1

D =

1 1 2

Zysków jednostkowych 1 2 1

C=<3,7, 5>

Limitów pracy :

B=<150, 170, 160> Znaleźć X*=<X1*, X2*, X3*> Tak aby:

CX* = max CX , przy spełnieniu warunków: DX≤B

Problem (2) Fabryka produkuje napoje gazowane w trzech różnych opakowaniach – szklanym, plastikowym oraz puszkach.

Przy produkcji każdego z opakowań wykorzystywana jedna z trzech maszyn.

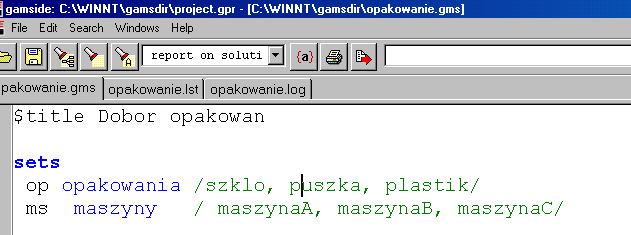
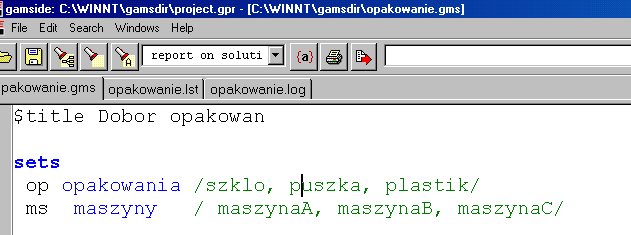
Zapis problemu w środowisku GAMS (1)

Zapis problemu w środowisku GAMS (2)

Zapis problemu w środowisku GAMS (3)

Zapis problemu w środowisku GAMS (4)

Zapis problemu w środowisku GAMS (5)

Zapis problemu w środowisku GAMS (6)