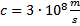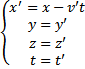
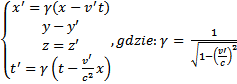
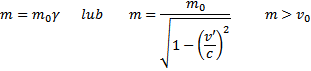
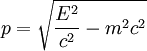
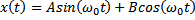
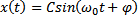
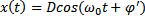
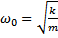
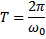
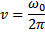
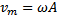
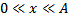
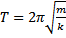
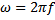
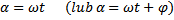
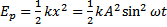
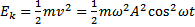
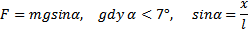
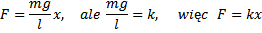
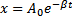
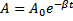
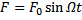
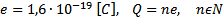
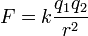
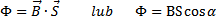
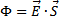
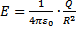
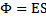
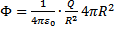
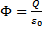
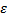
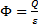
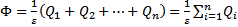
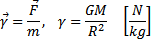
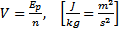
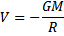
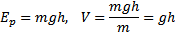
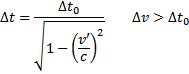
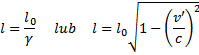
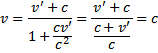
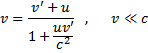
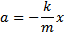
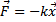
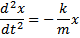
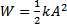
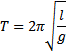
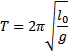
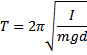
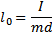
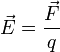
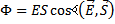
Natężenie pola grawitacyjnego stosunek siły grawitacji Energia w ruchu harmonicznym:

działającej na umieszczone w tym punkcie

ciało próbne do masy tego ciała. Jest to

wielkość wektorowa. Kierunek i zwrot

wektora natężenia jest taki sam, jak kierunek i zwrot wektora siły grawitacji (do źródła);

Wahadło matematyczne- to wyidealizowane wahadło proste, Potencjałem w danym punkcie pola

czyli mała kulka (punkt materialny) o masie m

nazywamy stosunek energii potencjalnej

zawieszona na nieważkiej i nierozciągliwej nici w

ciała o masie m umieszczonego w tym

jednorodnym polu grawitacyjnym. Siłą wprawiającą

punkcie do masy tego ciała;

wahadło w ruch jest wypadkowa siły ciężkości mg i

Potencjał pola grawitacyjnego w danym punkcie pola

reakcji nici Fn. Wartość wypadkowej siły:

informuje, jaką energię potencjalną miałoby

umieszczone w tym punkcie ciało o masie 1 kg. Ze

Wahadło fizyczne- bryła sztywna, która może wykonywać wzrostem odległości R danego punktu od źródła

obroty dookoła poziomej osi

potencjał grawitacyjny wzrasta.

przechodzącej ponad

Potencjał pola jest liniową funkcją

środkiem ciężkości tej

wysokości.

bryły.

d - odległość od punktu

Po

stulaty Einsteina szczególnej teorii wzgl ę

dn

o ś

c i:

zawieszenia do środka ciężkości; I – moment bezwładności ciała 1. Prędkość światła jest taka sama względem każdego

Ruch harmoniczny tłumiony: Drgania odbywające się w war.

inercjalnego układu odniesienia

; 2. We wszystkich

rzeczywistych, w dow. ośrodku materialnym, zawsze wiążą się z inercjalnych układach prawa fizyki mają taką samą postać i

przekazywaniem en. otoczeniu w zw. z pokonywaniem sił oporu.

zjawiska fizyczne przebiegają jednakowo;

W wyn. wyk. pracy energia ciała drgającego maleje, zmienia się Transformacje to układ równań pozwalający wyznaczyć

też A drgań. Drgania niepodtrzymywane siłą zewn. ulegają

współrzędne punktu czasoprzestrzeni w drugim układzie

tłumieniu, stopniowo zmn. swoją A i zanikają.

inercjalnym, jeśli znane są współrzędne punktu czasoprzestrzeni Wychylenie:

, A0- amplituda początkowa;

w pierwszym układzie inercjalnym.

, β- współczynnik tłumienia;

Ruch harmoniczny wymuszony: Drgania ciała może wywołać 1.

2.

zewn. siła zmieniająca się okresowo, tzn siła wymuszająca

. Drgania wymuszone mają częstotliwość V taką

samą, jak okresowo zmienna siła, ale na ogół różną od

1. transformacje Galileusza, 2. transformacje Lorentza;

częstotliwości własnej ciała. Jeżeli częstotliwość siły

Składanie szybkości wg Einsteina Jeżeli cząstka znajdująca wymuszającej i częstotliwość drgań własnych są sobie równe,

się w układzie O’ ma szybkość u względem tego układu, to

A = max (rezonans).

względem obserwatora O jej szybkość wynosi:

Wielkość ładunku elektrycznego jest wielokrotnością

ładunku elementarnego e:

gdzie e - ładunek elementarny; n - ilość ładunków elementarnych;

Zasada zachowania ładunku – w układzie ciał izolowanych Dylatacja czasu- to wydłużenie odstępu czasu, jeżeli pomiar elektrycznie ładunek może się przemieszczać z jednego ciała do zostanie przeniesiony do innego niż własny ukł. odniesienia.

drugiego, ale jego całkowita wartość (suma algebraiczna) nie

∆t0- odstęp czasu pomiędzy dwoma

może ulec zmianie.

zdarzeniami, które zaszły w układzie, Prawo Coulomba Siła F wzajemnego oddziaływania dwóch w którym też znajdował się

punktowych ładunków elektrycznych q1 i q2 jest wprost obserwator mierzący ten odstęp

proporcjonalna do iloczynu tych ładunków i odwrotnie

∆t - odstęp czasu pomiędzy

proporcjonalna do kwadratu odległości między nimi r.

zdarzeniami, które zaszły w układzie O’, i zmierzony przez

obserwatora O;

k jest współczynnikiem proporcjonalności.

Relatywistyczna długość - Korzystając z transformacji Natężenie pola elektrycznego jest równe sile działającej na Lorentza, można łatwo wyprowadzić wzór na relatywistyczną

jednostkowy dodatni ładunek próbny, co

długość pręta ustawionego wzdłuż osi x i znajdującego się w

matematycznie wyraża się jako stosunek siły F→, z jaką

układzie O’.

pole elektrostatyczne działa na ładunek elektryczny, do

x2’-x1’=l0 - długość pręta

wartości q tego ładunku.

zmierzona, gdy pręt spoczywał Strumień indukcji magnetycznej przez płaską powierzchnię względem mierzącego

obserwatora; x

jest zdefiniowany wzorem:

gdzie:

2-x1=l - długość

pręta spoczywającego w układzie O’, lecz zmierzona przez

S- powierzchnia, przez która przechodzi strumień.

obserwatora O;

Wektory B i S mnożymy przez siebie skalarnie, strumień jest Masa relatywistyczna:

wielkością skalarną. Strumień = max, gdy wektor powierzchni S

jest równoległy do wektora B; Jednostką jest weber (Wb): 1Wb

= 1T ∙ 1m2;

Strumień natężenia pola elektrostatycznego

. S -

pole powierzchni S. Jeżeli kierunek wektora S nie jest prostopadły do powierzchni strumień

m

natężenia:

0 - masa spoczynkowa

Pr

awo Gaussa dla elektryczno ś

c i i magnetyzmu.

Prawo Gaussa dotyczy zależności strumienia natężenia pola

Pęd relatywistyczny:

elektrostatycznego przechodzącego przez dowolną powierzchnię zamkniętą od ładunku Q znajdującego się w obszarze objętym

Ruch harmoniczny ruch okresowy opisywany funkcją

tą powierzchnią. Jeżeli dodatni ładunek Q otoczony jest

sinusoidalną.

powierzchnią kulistą o promieniu R, w której środku się

znajduje, to linie sił wychodzą radialnie z tego ładunku, a

kierunek i zwrot wektora E pokrywa się z kierunkiem i zwrotem wektora S. Natężenie pola E w dowolnym punkcie tej Rozwiązania tego równania można równoważnie opisać za

pomocą dowolnej z poniższych funkcji:

powierzchni wynosi

, zatem strumień elektryczny

przechodzący przez powierzchnię kuli

,

A, B, C, φ, C, φ’- stałe zal. od

warunków;

w próżni jest równy

, a w

częstość kołowa drgań pocz.:

; okres:

środowisku o przenikalności ,

.

Całkowity strumień nie zależy od promienia kuli, przez którą częstotliwość drgań:

przechodzi, zależy natomiast od ładunku znajdującego się

wewnątrz i od przenikalności elektrycznej ośrodka. Otrzymana Prędkość w r. har. ciała ulega zmianie, zmienia się jej wartość zależność nie zmienia swej postaci przy zastąpieniu kuli i zwrot. W położeniu x=0 szybkość jest maksymalna

,

dowolną zamkniętą powierzchnią.

w położeniu x = A prędkość zmienia swój zwrot, a jej wartość prawo Gaussa: Strumień wektora natężenia pola

v=0; Pojęcia: położenie równowagi (punkt 0); A – amplituda, elektrostatycznego E przechodzący przez dowolną zamkniętą czyli maksymalne wychylenie z położenia równowagi; x –

powierzchnię S jest równy całkowitemu ładunkowi zawartemu

wychylenie,

; T – okres, czyli czas, w którym ciało

wewnątrz tej powierzchni podzielonemu przez przenikalność

elektryczną ośrodka. Jeżeli w zamkniętej powierzchni znajduje wykonuje jedno pełne drganie, okres drgań oscylatora

się n ładunków Q1, Q2, …Qn (dodatnich i ujemnych), to całkowity harmonicznego

; f – częstotliwość drgań;

strumień elektryczny przechodzący przez tę powierzchnię

ω – częstość kołowa,

; α – faza drgań (kąt, jaki tworzy wynosi

.

promień okręgu z osią x)

; φ – faza

początkowa (gdy w momencie pocz., dla t = 0, ciało nie znajduje się w poł. równowagi, lecz ma wychylenie x)