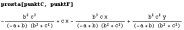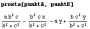m a t e m a t y k a
Nie milkną spory o maturze, która w nowym
Czysta geometria, prawda? Nie chcia³o mi siê
ujęciu czeka uczniów (a więc wielu naszych
myœleæ. W³¹czy³em program, który narysowa³ mnie taki
rysunek, jak wy¿ej i jeszcze „zanimowa³”. Wszystko siê
Czytelników) za kilka miesięcy. Przez ten czas rusza³o. Trójk¹t zmienia³ kszta³t, a proste AE i CF za-w kąciku matematycznym będzie o tej matu-
wsze sta³y do siebie ortogonalnie. Jak drut. „No, to siê
zgadza”, pomyœla³em i w³aœciwie straci³em zaintereso-
rze - ale ogólnie. Poradników szczegółowych
wanie. Wszyscy widzimy, ¿e siê zgadza. Po co wiêc da-
jest bardzo dużo. A mnie chodzi o ogólne spoj- lej rozdzielaæ w³os na czworo? Istnieje powiedzenie, ¿e dowody twierdzeñ matematycznych s¹ w ogóle niepo-rzenie - przyda się ono i młodym, i starszym.
trzebne, bo je¿eli twierdzenie jest prawdziwe, to po co
jeszcze dowód, a je¿eli nieprawdziwe, to i tak siê udo-
Środowisko naukowe i nauczycielskie jest konserwa- wodniæ nie da.
tywne. To dobrze. Wychowanie i nauczanie powinno
Program, o którym mówiê, jest autorstwa nie-
siê opieraæ na solidnych, sprawdzonych podsta-
mieckiego profesora Grothmanna. Jest freeware, w
wach. Reformy winny byæ powolne i starannie przygo-
wersji angielskiej nazywa siê c.a.r (compass and ruler),
towane. Ale konserwatyzm ma swoje z³e strony. Wci¹¿
w niemieckiej Z.u.L (Zirkel und Lineal). Mo¿na go (pro-
bronimy siê przed dopuszczeniem na egzaminy urz¹-
gram, nie profesora, i to w wersji polskiej) legalnie za-
dzeñ licz¹cych, z kalkulatorami na czele. Wielu uczo-
instalowaæ na swoim komputerze, wyszukuj¹c po na-
nych i wielu wyk³adowców starszej daty nie dostrzega,
zwisku lub po nazwie programu.
¿e komputery po prostu s¹, ¿e uczyæ trzeba inaczej.
KOMPUTER I ZADANIE
M i c h a ł S z u r e k
Z OLIMPIADY MATEMATYCZNEJ
Jak? W tym w³aœnie problem - nie na ³amy „M³odego
No tak, ale to niegodne matematyka. Zacz¹³em
Technika”.
myœleæ, ale w moim wieku nie jest to ju¿ takie ³atwe.
Jerzy Hajdukiewicz, polski himalaista lat szeœædziesi¹-
Skalê trudnoœci ujmuje autentyczna historia z za-
tych XX wieku, napisa³ kiedyœ artyku³ „Stary cz³owiek
daniem z Olimpiady Matematycznej (paŸdziernik 2004).
w górach”. Nie wiem, czy napiszê artyku³ „Stary cz³o-
Ubarwiê nieco fabu³ê, zachowuj¹c istotê sprawy. Zada-
wiek i matematyka”, ale ¿e myœleæ mi siê nie chce, to
nie by³o oto takie:
fakt.
W trójk¹cie ostrok¹tnym (rysunek) punkt D jest
Bo mo¿na obejœæ siê bez myœlenia. Wprowadzi-
spodkiem wysokoœci poprowadzonej z C na AB, punkt ³em uk³ad wspó³rzêdnych tak, by punkty A, B, C mia³y E jest rzutem D na CB, zaœ punkt F dzieli odcinek odpowiednio wspó³rzêdne ( a, 0), ( b, 0), (0, c), zaœ po-cz¹tek uk³adu by by³ w punkcie D. Nauczy³em program
AB
EF
DE tak, ¿e .
=
Mathematica, jak prowadziæ prost¹ przez dwa punkty
DB
FD
(to znaczy jak obliczyæ jej równanie!), jak prost¹ prosto-
Wykazaæ, ¿e proste AE i CF s¹ prostopad³e.
pad³¹ itp. Po naciœniêciu Enter, nim mój kot merdn¹³
ogonem, mia³em na ekranie wszystkie wspó³rzêdne
i równania:
C
punktE = {b*c^2/(b^2+c^2), b^2*c/(b^2+c^2)};
punktF = {b^2*c^2/(b–a)/(b^2+c^2), b^3*c/(b–a)/(b^2+c^2)};
Nawet nie chcia³o mi siê sprawdziæ, czy rzeczy-
M
wiœcie CF jest prostopad³e do AE. Móg³bym obliczyæ Ł
stosowny iloczyn skalarny, ale czy to warto? Na pewno
ODY
wyjdzie zero - wiêc po co jeszcze chleb, Króliku? Dla
rozrywki wyliczy³em równania prostych (dok³adniej:
TECHNIK
„lewe strony” tych równañ):
G
E
β δ
ε
A
D F
H B
52
11
/2004
K o m p u t e r y p o p r o s t u s ą i m o ż e c o ś z t e g o p o w i n n o w r e s z c i e w y n i k a ć
In[1]= Simplify [(Tan[beta] + q*Sin[beta]*Cos[beta] / (p + q*Sin[beta]^2))/
(1 – Tan[beta] * (q*Sin[beta]*Cos[beta]) / (p + q*Sin[beta]^2))]
Out[1]= –––
(p + q)
––––––p–––––
Tan[beta]
––– .
ale nie odkry³em niczego specjalnie ciekawego i zacz¹-
³em siê zastanawiaæ nad rozwi¹zaniem bardziej god-
Zadanie rozwi¹zane, bo w³aœnie to jest tangens δ.
nym matematyka. Ociê¿a³oœæ umys³owa znów da³a
znaæ o sobie. Wzi¹³em siê za trygonometriê - tam my-
W tym momencie ju¿ zupe³nie odechcia³o mi siê
œleæ nie trzeba, bo samo idzie. Oznaczy³em punkty jak
myœleæ... Ale po chwili zacz¹³em - lecz ju¿ nie jak roz-
na rysunku. Punkt G to punkt wspólny prostych AE
wi¹zaæ zadanie, tylko nad sprawami ogólniejszymi. Czy
i CF. Trzeba wykazaæ, ¿e k¹t G ma 90 stopni.
Komitet Olimpiady Matematycznej uzna³by takie roz-
Zauwa¿my, ¿e k¹t CDE jest te¿ równy β, k¹towi
wi¹zanie (to znaczy: weŸ komputer i wylicz)? A po dru-
trójk¹ta przy wierzcho³ku B. Popatrzmy na trójk¹ty pro-
gie: sposób drugi jest tak prosty i bezmyœlny, ¿e algo-
stok¹tne CED i CEF. Z warunków zadania i definicji rytm da siê przes³aæ SMS-em. Próbowa³em: umiem siê
tangensa wynika, ¿e
z zapasem zmieœciæ w trzech (po 160 znaków). Czy da
siê kompletny dowód (bo rachunki s¹ oczywiste) zmie-
tg δ
CE
CE
DE
FE + DF
q
p + q
œciæ w jednym SMS-ie? Czy Komitet bêdzie kiedyœ
=
:
=
=
= 1+ =
,
tg β
FE
DE
FE
FE
p
p
uznawaæ tak opracowane dowody?
NIECH H RZUT E NA AB NIECH G WSPOLNY
gdzie p jest d³ugoœci¹ odcinka AD, zaœ q - d³ugoœci¹
AE,CF WTEDY KAT CDE= CDB Z WAR ZAD POROWN
odcinka DB. Wyliczmy st¹d tangens δ :
TG CFE I TG CDE WYLICZ LATWIUTKO DH I TG EAB
W 4KACIE AGFD SUMA 360 STOPNI ZASTOS WZOR
p + q
NA SUME TG (EDC+EAB)I WYLICZ ZE AGF PROSTY.
tg δ =
⋅ tg β .
p
Coraz wiêcej zadañ z konkursów umiem rozwi¹-
zaæ w³aœnie tak. Czy to oznaka starzenia siê? Mojego
Na koñcu oka¿e siê, ¿e to by³o wa¿ne.
czy... konkursów?
Nie tylko w matematyce, ale w ka¿dej nauce
Standardowa analiza zale¿noœci w trójk¹tach
i mo¿e we wszystkim, co robimy, piêkne jest stosowa-
DEB i HEB daje - myœleæ prawie nie trzeba - zale¿noœci: nie nowych, nieoczekiwanych i pomys³owych metod.
Dotyczy to naprawdê wszystkich obszarów dzia³alnoœci
DE = q sin β ; EB = q cos β ; EH = DE sin (90° – β) = q ludzkiej. Przypomnijmy sobie rewolucyjne zmiany, które
sin β cos β ;
dokona³y siê w muzyce za spraw¹ Bacha, a póŸniej Mo-
zarta. Przypomnijmy sobie wymyœlony przez Johna
HD = DE cos (90° – β) = DE sin β = q sin2 β .
Fossbury’ego powszechny dziœ styl skakania wzwy¿
(„flop”). Przypomnijmy sobie kubistów w malarstwie
Zatem patrz¹c na trójk¹t AEH i stosuj¹c definicjê tan-
(oczywiœcie zdarza siê bezsensowne nowatorstwo, za
gensa, mamy:
które pisz¹cy te s³owa uwa¿a turpizm, czyli zachwyt
nad brzydot¹, np. twórczoœæ Jerzego Dudy-Gracza).
EH
q sin β cos β
tg ε
W samej matematyce rozwi¹zanie 350-letniego proble-
=
=
2
.
AH
p + q sin β
mu Fermata by³o mo¿liwe dziêki zastosowaniu metod
z zupe³nie innej dyscypliny matematycznej, mianowicie
A teraz skierujmy wzrok na czworok¹t AGFD.
geometrii algebraicznej. I tak dalej.
Jak by tu wykazaæ, ¿e k¹t przy wierzcho³ku G jest pro-
Jeœli ktokolwiek zastanawia siê nad „praktyczn¹
sty? Ojej, co za problem? Oznaczmy ten k¹t przez ξ. To
filozofi¹” matematyki, to dostrzega dwie przeciwne
³adna grecka litera. Lubiê j¹. Suma k¹tów czworok¹ta
tendencje: ograniczania stosowanych metod i rozpatry-
AGFD jest równa 360 stopni. No, to dodawajmy:
wania zagadnieñ w jak najszerszej ogólnoœci. S¹ to
ε + ξ + (180° – δ) + (β + 90°) = 360° .
przeciwne, ale nie sprzeczne tendencje. Zawodowych
A zatem jeœli wyka¿emy, ¿e β + ε = δ , to bêdzie
matematyków raduje zarówno dowód taki, w którym
dobrze. Nie myœleæ, nie myœleæ... Jak w jednym z opo-
u¿ywamy jak najskromniejszych œrodków, jak i ten, w
wiadañ Stanis³awa Lema - tam robot porusza³ siê na
którym szczegó³owe zadanie okazuje siê nam w ca³ej
planecie z zamro¿onej rtêci, a ¿e myœlenie powodowa³o
ogólnoœci - niekiedy w bardzo ogólnej ogólnoœci....
wzrost temperatury, wiêc warunkiem przetrwania by³a
Ale ka¿dy z radoœci¹ patrzy na zagadnienia,
bezmyœlnoœæ. Jakie to wspó³czesne... Jako ¿ywo, histo-
w których mo¿na powiedzieæ: „Dorysuj jedn¹ kreskê,
ria est magistra vitae.
a rozwi¹¿esz!”. Przeczuwa³em, ¿e w tym zadaniu wy-
M
Oczywiste: wystarczy porównaæ tangensy - czy
starczy tak¹ kreskê narysowaæ. Ale gdzie?
ŁODY
tangens β + ε jest równy tg δ. To jeszcze pamiêtam ze
Honorarium, jakie dostanê za ten artyku³, z na-
szko³y:
wi¹zk¹ przewy¿szy koszt telefonów do kolegi ze Szcze-
TECHNIK
cina. Bo to on dostawi³ ow¹ kreskê. Có¿, m³odoœæ...
tgβ + tg ε
Trzeba poprowadziæ DK równolegle do AE, punkt K to tg(β + ε ) =
.
1− tgβ tgε
ten, gdzie owa prosta przecina CB. W trójk¹cie DEK k¹t przy wierzcho³ku K jest równy β + ε .
Komputerze, nie kuœ... program Mathematica da³ odpo-
wiedŸ.
53
11
/2004
Bardzo zwraca siê na to uwagê w szkole amery-
C
kañskiej i w ogóle w amerykañskim wychowaniu. Pra-
ca w zespole. Teamwork. To prawda, ¿e niekiedy prze-
szkadzamy sobie wzajemnie - jak tych stu robotników
kopi¹cych studniê w 10 minut... Ale tylko niekiedy. Nie
wszystko, co pochodzi z Ameryki, jest niedobre.
I jeszcze jeden wniosek. Mo¿e najwa¿niejszy. Jeœli
robimy coœ razem, daje to po prostu wiêcej satysfakcji.
A dla Czytelników, którzy chcieliby jakieœ ³a-
twiejsze zadanie, zwi¹zane z tym zagadnieniem, pole-
G
E
cam nastêpuj¹ce: w trójk¹cie równobocznym przepro-
wadzamy analogiczn¹ konstrukcjê na ka¿dym boku; to
β δ
K
znaczy rzutujemy wierzcho³ek na przeciwleg³y bok,
ε
spodek wysokoœci rzutujemy na bok i otrzymujemy - jak
A
D F
H B
wy¿ej punkty G1, G2, G3. Tworz¹ one trójk¹t równo-I dalej jak po maœle: tangens tego k¹ta to
boczny. Jak¹ d³ugoœæ ma jego bok?
DE
DE
DE
AB
* * *
==
= tg β ⋅
.
Podsumujmy. Komputer „pomóg³”, „podsun¹³ po-
EK
EB − BK
EB − DB
AD
EB −
mys³”, a wreszcie dziêki swojej mocy obliczeniowej
AB
„rozwi¹za³” ca³e zadanie. To oczywiœcie nieprawda. To
I mamy cel: dowód jak najprostszymi metodami. Wynik
nie komputer. Tylko ja. Cz³owiek. Komputer potrzebny
pracy zespo³owej jest zwykle wiêkszy ni¿ suma wyni-
by³ mi jak tyczka Siergiejowi Bubce. Ani Bubka bez
ków, które osi¹gnêliby w pojedynkê cz³onkowie zespo-
tyczki nie skoczy³by 6 metrów. Ale tyczka bez Bubki sa-
³u. Jeœli piêciu robotników wnosi fortepian na pi¹te
ma by nawet pó³ metra nie przeskoczy³a. Ba, nawet...
piêtro w 15 minut, to w jakim czasie jeden robotnik
Komputery prêdzej czy póŸniej wkrocz¹ do szkó³
wniós³by fortepian na 60. piêtro? Takie zadanie umiemy
pe³nym frontem, nie tylko jako koñcówki do Internetu.
rozwi¹zaæ. W 15 godzin. Bez komentarza.
!
MŁODY
TECHNIK
54
11
/2004