LABORATORIUM MECHANIKI EKSPERYMENTALNEJ

Instrukcja do ćwiczenia

Wyznaczanie momentów bezwładności elementów

2

maszyn metodą podwieszenia trójpunktowego

Cel ćwiczenia

Celem ćwiczenia jest zapoznanie z eksperymentalnymi metodami wyznaczania momentów bezwładności części maszyn oraz porównanie ich z metodami analitycznymi. W ramach realizowanego ćwiczenia, wykorzystuje się metodę podwieszenia trójpunktowego.

Literatura

1. J.Leyko, Mechanika Ogólna, tom II.

2. K.Zarankiewicz, Mechanika Teoretyczna, tom III, rozdz. X.

Zagadnienia kontrolne

1. Definicje momentów bezwładności ciała sztywnego: a) względem płaszczyzny,

b) względem osi,

c) względem punktu.

2. Umiejętność wyznaczenia sposobem analitycznym momentów bezwładności prostych ciał jednorodnych, jak: walec, kula, stożek, stożek ścięty itp.

3. Twierdzenie Steinera.

4. Analityczne wyznaczenie momentów bezwładności ciała złożonego z prostych elementów.

5. Dynamiczne równanie ruchu obrotowego ciała sztywnego.

6. Umiejętność tworzenia dynamicznych równań ruchu ciała sztywnego w ruchu obrotowym.

Uwaga. Instrukcja dotyczy podstaw samego ćwiczenia. Aby opanować powyższe zagadnienia należy sięgnąć do podanej literatury.

Podstawy teoretyczne dotyczące przeprowadzenia eksperymentu

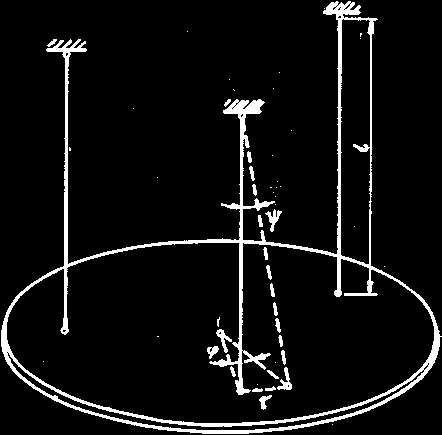
Rozpatrzymy swobodne drgania obrotowe układu, w którym na trzech jed-nakowych niciach zawieszono kołową tarczę o masie mt. Układ ten pokazano schematycznie na rys.1. Tarcza zawsze powinna się znajdować w położeniu poziomym.

Rys.1. Schemat układu dla metody trójpunktowego podwieszenia Na tarczy kładziemy element o masie m e. Równanie dynamiczne ruchu obrotowego układu, składającego się z tarczy i badanego elementu, ma postać: ( J

ϕ&&

(1)

t + J e )

+ M = 0

gdzie: Jt - moment bezwładności tarczy względem osi symetrii prostopadłej do płaszczyzny tarczy,

Je - moment bezwładności elementu względem tej samej osi, M - moment, względem tej samej osi, sił oddziaływujących na tarczę wychyloną z położenia równowagi,

ϕ - kąt obrotu tarczy.

Moment sił M można określić zależnością:

M = g( m + m

(2)

t

e ) r tgψ

gdzie: r - odległość linki od osi tarczy, ψ - kąt wychylenia linki.

Dla małych kątów (ψ <10°) mo żna przyjąć, że t ψ

g

≈ψ . Wówczas zależność (2)

przyjmie postać:

M ≈ g( m + m

t

e ) r ψ

(3)

Dla małych kątów można zapisać następującą zależność: τ = rϕ ≈ lψ

(4)

r

ψ = ϕ

l

gdzie l – długość linki.

Uwzględniając zależności (1), (2), (4) , otrzymamy ostateczną postać równania ruchu układu :

g( mt + me ) 2

ϕ&& +

r

(

ϕ

(5)

Jt + Je )

= 0

l

Tak więc, częstość drgań własnych układu wynosi:

g( m + m

2

t

e ) r

ω =

(

.

(6)

J + J

t

e ) l

Ponieważ okres wahań układu wynosi:

π

2

T = ω ,

(7)

stąd okres wahań układu tarczy i elementu na niej spoczywającej wynosi: ( J + J l

t

e )

T = π

2

(8)

r

g( m + m

t

e )

Gdy na linkach wisi tylko tarcza, to okres wahań wynosi: π

2

J l

t

T =

(9)

t

r

gmt

Znając okres drgań T i okres drgań Tt można wyznaczyć z zależności (8) i (9) moment bezwładności tarczy Jt i moment bezwładności Je: m gr T

2

2

J

t

t

=

[

2

kg ⋅ m ]

(10a)

t

2

4π l

gr T

2

2 ( m + m

t

e )

J =

− J

[

2

kg ⋅ m

(10b)

e

2

t

4π

]

l

Oszacowanie niepewności pomiarowej

Załóżmy dalej, że niepewności poszczególnych pomiarów są niezależne i losowe.

Ogólna zależność określająca jak się przenoszą błędy wielkości mierzonych na wyznaczaną pośrednio wielkość, przy założeniu niezależności błędów wielkości mierzonych, przedstawia się następująco1:

2

2

 ∂ y



 ∂ y



∆ y = 

∆ x + ... + 

∆ z

 ∂ x



 ∂ z



(11)

gdzie y( x,.. z) jest wielkością wyznaczaną metodą pośrednią na podstawie pomiaru wartości x,.. . z.

Niepewność wyznaczenia Jt metodą pośrednią można oszacować jako: 2

2

2

2

2









∂ Jt

∂ J



t

∂ J







t

∂ J



t

∂ J















∆ J

(12)

t =

∆ mt +

∆ g +

t











∆ r  +

∆ Tt +







∆ l 

 ∂ mt



 ∂ g



 ∂ r



 ∂ Tt



 ∂ l



gdzie:

m

∆ , g

∆ , r

∆ , T

∆ , l

∆ są niepewnościami pomiarowymi wielkości mierzonych t

t

bezpośrednio: masy tarczy, przyspieszenia ziemskiego, odległości zaczepienia linki do środka tarczy, okresu wahań tarczy, długości linki.

Ostatecznie można zapisać, że niepewność oszacowania momentu bezładności tarczy wynosi:

2 

 rT 

2

2

2

2

 2 m grT

2

∆ Jt = 

t

  grT m

m rT g

2 m gT

r

2 m gr T

t

t

l

2

( t∆ t) + ( t t∆ ) + ( t t ∆ ) + ( t ∆ t)



+ 

∆  

 4π l  



l

 

[

2

kg ⋅ m ]

(13)

Podobnie oszacowanie niepewności wyznaczonego momentu bezwładności elementu można oszacować jako:

2

2

 rT  

 2 MgrT





J

∆ =

2 grT M





∆

+ MrT g

∆

+ 2 MgT r

∆

+ 2 Mgr T

∆

+ 

l

∆   + J

∆

e

2

(

)2 (

)2 (

)2 (

)2

2

 4

t

π

l  



l



 

[

2

kg ⋅ m ]

(14)

gdzie: M = m + m , oraz przyjęto M

∆ = m

∆ = m

∆

t

e

e

t

1 Aby poszerzyć wiedze z tego zakresu sięgnij po książkę: John R. Taylor; Wstęp do analizy błędu pomiarowego; PWN Warszawa 1999 i późniejsze wydania (rozdział 3).

Przebieg ćwiczenia

Zdjęcie stanowiska przedstawiono na rysunku 2.

Rys. 2. Stanowisko do badań momentu bezwładności, oraz przyrząd do pomiaru czasu 10 wahnięć tarczy

Opis kolejnych kroków, które należy wykonać, znajduje się w arkuszu sprawozdania.

Poniżej zwrócono uwagę na pewne istotne zagadnienia.

• Przy pomiarze czasu 10 –ciu wahnięć samej tarczy jak i układu tarcza-element należy uważać, aby maksymalny kąt odchylenia tarczy nie przekraczał 10o.

• Element należy umieścić na tarczy w ten sposób, aby oś, względem której ma być wyznaczony moment bezwładności, pokrywała się z osią obrotu tarczy

• Ponieważ długości linek mogą nie być identyczne, podobnie jak odległości ich zamocowania od osi tarczy, należy odpowiednie wartości uśrednić z pomiarów wykonanych dla wszystkich trzech linek.

• Przy analitycznych obliczeniach momentu bezwładności elementu można skorzystać z zestawienia gęstości materiałów zamieszczonego poniżej.

• We wnioskach należy się ustosunkować do otrzymanych pomiarów, a w szczególności różnic pomiędzy otrzymanymi wartościami uzyskanymi z obliczeń analitycznych oraz z eksperymentu. Przy porównaniu wyników należy uwzględnić otrzymane oszacowanie niepewności pomiarowej.

Materiał

Gęstość [kg/m3]

Mosiądz

8500

Stal

7800

Bakelit

1100 - 1600

Ebonit

1400 - 1800

Duraluminium

2750