wer. 2014 MT

1

LABORATORIUM MECHANIKI EKSPERYMENTALNEJ

Instrukcja do ćwiczenia

2

Wyznaczanie momentów bezwładności elementów

maszyn metodą podwieszenia trójpunktowego

Cel

ć

wiczenia

Celem

ć

wiczenia jest zapoznanie z eksperymentalnymi metodami wyznaczania

momentów bezwładno

ś

ci cz

ęś

ci maszyn oraz porównanie ich z metodami

analitycznymi. W ramach realizowanego

ć

wiczenia, wykorzystuje si

ę

metod

ę

podwieszenia trójpunktowego.

Literatura

1. J.Leyko, Mechanika Ogólna, tom II.
2. K.Zarankiewicz, Mechanika Teoretyczna, tom III, rozdz. X.

Zagadnienia kontrolne

1. Definicje masowych momentów bezwładno

ś

ci bryły sztywnej i układu punktów

materialnych:

a) wzgl

ę

dem płaszczyzny,

b) wzgl

ę

dem osi,

c) wzgl

ę

dem punktu.

2. Zale

ż

no

ś

ci pomi

ę

dzy momentami bezwładno

ś

ci w prostok

ą

tnym układzie

współrz

ę

dnych (np. momentem biegunowym a momentami wzgl

ę

dem trzech

prostopadłych osi).
3. Moment dewiacyjny dla układu punktów materialnych i bryły sztywnej
4. Twierdzenie Steinera dla osi równoległych i umiej

ę

tno

ść

jego stosowania przy

wyznaczaniu momentu bezwładno

ś

ci

5. Masowe momenty bezwładno

ś

ci wzgl

ę

dem osi: walca, pr

ę

ta, prostopadło

ś

cianu,

płyty prostok

ą

tnej, tarczy kołowej, pier

ś

cienia – wzory i umiej

ę

tno

ść

stosowania

6. Promie

ń

bezwładno

ś

ci i masa zredukowana dla momentów bezwładno

ś

ci

7. Główne i główne centralne osie bezwładno

ś

ci

8. Dynamiczne równanie ruchu obrotowego bryły sztywnej
9. Zale

ż

no

ść

pomi

ę

dzy cz

ę

sto

ś

ci

ą

kołow

ą

a okresem

10. Analityczne wyznaczenie momentów bezwładno

ś

ci ciała zło

ż

onego z prostych

elementów
11. Zasadniczy przebieg

ć

wiczenia

Uwaga!
Instrukcja dotyczy podstaw samego

ć

wiczenia. Aby opanowa

ć

powy

ż

sze

zagadnienia nale

ż

y si

ę

gn

ąć

do podanej literatury.

wer. 2014 MT

2

1. Podstawy teoretyczne dotyczące przeprowadzenia eksperymentu

Rozpatrzymy swobodne drgania obrotowe układu, w którym na trzech jed-

nakowych niciach zawieszono kołow

ą

tarcz

ę

o masie m

t

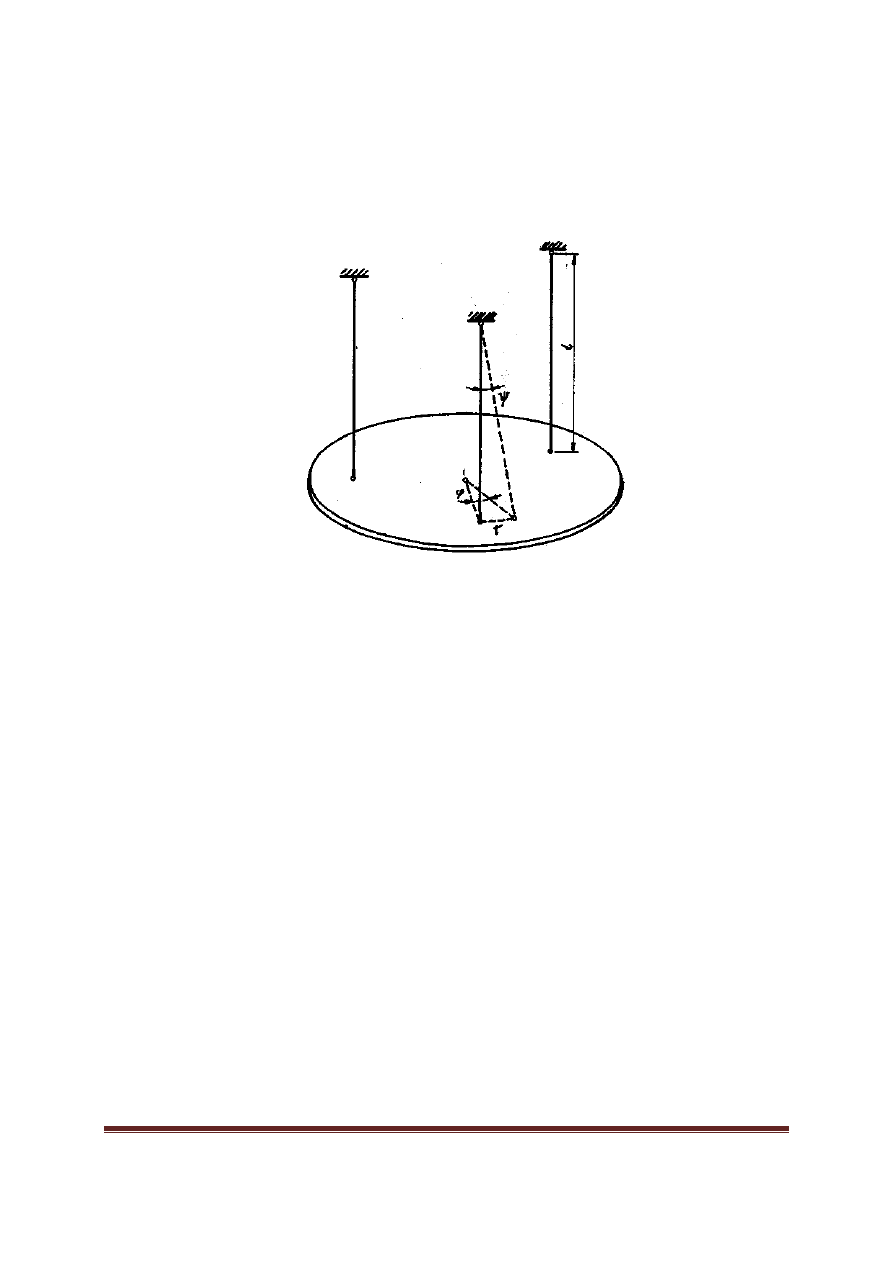
. Układ ten pokazano

schematycznie na rys.1. Tarcza zawsze powinna si

ę

znajdowa

ć

w poło

ż

eniu

poziomym.

Rys.1. Schemat układu dla metody trójpunktowego podwieszenia

Na tarczy kładziemy element o masie m

e

. Równanie dynamiczne ruchu

obrotowego układu, składaj

ą

cego si

ę

z tarczy i badanego elementu, ma posta

ć

:

(

)

0

=

+

+

M

J

J

e

t

ϕ

&

&

(1)

gdzie: J

t

- moment bezwładno

ś

ci tarczy wzgl

ę

dem osi symetrii prostopadłej do

płaszczyzny tarczy,
J

e

- moment bezwładno

ś

ci elementu wzgl

ę

dem tej samej osi,

M - moment, wzgl

ę

dem tej samej osi, sił oddziaływuj

ą

cych na tarcz

ę

wychylon

ą

z poło

ż

enia równowagi,

ϕ

- k

ą

t obrotu tarczy.

Moment sił M mo

ż

na okre

ś

li

ć

zale

ż

no

ś

ci

ą

:

(

)

ψ

tg

r

m

m

g

M

e

t

+

=

(2)

gdzie: r - odległo

ść

linki od osi tarczy,

ψ

- k

ą

t wychylenia linki.

Dla małych k

ą

tów (

ψ

<10°) mo

ż

na przyj

ąć

,

ż

e

ψ

ψ

≈

tg

. Wówczas zale

ż

no

ść

(2)

przyjmie posta

ć

:

(3)

(

)

ψ

r

m

m

g

M

e

t

+

≈

wer. 2014 MT

3

Dla małych k

ą

tów mo

ż

na zapisa

ć

nast

ę

puj

ą

c

ą

zale

ż

no

ść

:

(4)

gdzie l – długo

ść

linki.

Uwzgl

ę

dniaj

ą

c zale

ż

no

ś

ci (1), (2), (4) , otrzymamy ostateczn

ą

posta

ć

równania ruchu

układu :

(

)

(

)

0

2

=

+

+

+

ϕ

ϕ

l

J

J

r

m

m

g

e

t

e

t

&

&

(5)

Tak wi

ę

c, cz

ę

sto

ść

drga

ń

własnych układu wynosi:

(

)

(

)

l

J

J

r

m

m

g

e

t

e

t

+

+

=

2

ω

.

(6)

Poniewa

ż

okres waha

ń

układu wynosi:

ω

π

2

=

T

,

(7)

st

ą

d okres waha

ń

układu tarczy i elementu na niej spoczywaj

ą

cej wynosi:

(

)

(

)

e

t

e

t

m

m

g

l

J

J

r

T

+

+

=

π

2

(8)

Gdy na linkach wisi tylko tarcza, to okres waha

ń

wynosi:

t

t

t

gm

l

J

r

T

π

2

=

(9)

Znaj

ą

c okres drga

ń

T i okres drga

ń

T

t

mo

ż

na wyznaczy

ć

z zale

ż

no

ś

ci (8) i (9)

moment bezwładno

ś

ci tarczy J

t

i moment bezwładno

ś

ci J

e

:

l

T

gr

m

J

t

t

t

2

2

2

4

π

=

]

[

2

m

kg

⋅

(10a)

(

)

t

e

t

e

J

l

m

m

T

gr

J

−

+

=

2

2

2

4

π

]

[

2

m

kg

⋅

(10b)

ϕ

ψ

l

r

=

ψ

ϕ

τ

l

r

≈

=

wer. 2014 MT

4

2. Oszacowanie niepewno

ś

ci pomiarowej

Załó

ż

my dalej,

ż

e niepewno

ś

ci poszczególnych pomiarów s

ą

niezale

ż

ne i losowe.

Ogólna zale

ż

no

ść

okre

ś

laj

ą

ca jak si

ę

przenosz

ą

bł

ę

dy wielko

ś

ci mierzonych na

wyznaczan

ą

po

ś

rednio wielko

ść

, przy zało

ż

eniu niezale

ż

no

ś

ci bł

ę

dów wielko

ś

ci

mierzonych, przedstawia si

ę

nast

ę

puj

ą

co

1

:

2

2

...













∆

∂

∂

+

+













∆

∂

∂

=

∆

z

z

y

x

x

y

y

(11)

gdzie y(x,..z) jest wielko

ś

ci

ą

wyznaczan

ą

metod

ą

po

ś

redni

ą

na podstawie pomiaru

warto

ś

ci x,...z.

Niepewno

ść

wyznaczenia J

t

metod

ą

po

ś

redni

ą

mo

ż

na oszacowa

ć

jako:

2

2

2

2

2













∆

∂

∂

+















∆

∂

∂

+













∆

∂

∂

+













∆

∂

∂

+















∆

∂

∂

=

∆

l

l

J

T

T

J

r

r

J

g

g

J

m

m

J

J

t

t

t

t

t

t

t

t

t

t

(12)

gdzie:

l

T

r

g

m

t

t

∆

∆

∆

∆

∆

,

,

,

,

s

ą

niepewno

ś

ciami pomiarowymi wielko

ś

ci mierzonych

bezpo

ś

rednio: masy tarczy, przyspieszenia ziemskiego, odległo

ś

ci zaczepienia linki

do

ś

rodka tarczy, okresu waha

ń

tarczy, długo

ś

ci linki.

Ostatecznie mo

ż

na zapisa

ć

,

ż

e niepewno

ść

oszacowania momentu bezładno

ś

ci

tarczy wynosi:

(

) (

)

(

)

(

)



























∆

+

∆

+

∆

+

∆

+

∆













=

∆

2

2

2

2

2

2

2

2

2

2

4

l

l

grT

m

T

gr

m

r

gT

m

g

rT

m

m

grT

l

rT

J

t

t

t

t

t

t

t

t

t

t

t

t

π

]

[

2

m

kg

⋅

(13)

Podobnie oszacowanie niepewno

ś

ci wyznaczonego momentu bezwładno

ś

ci

elementu mo

ż

na oszacowa

ć

jako:

(

) (

) (

) (

)

2

2

2

2

2

2

2

2

2

2

2

2

4

t

e

J

l

l

MgrT

T

Mgr

r

MgT

g

MrT

M

grT

l

rT

J

∆

+



























∆

+

∆

+

∆

+

∆

+

∆













=

∆

π

]

[

2

m

kg

⋅

(14)

gdzie:

e

t

m

m

M

+

=

, oraz przyj

ę

to

t

e

m

m

M

∆

=

∆

=

∆

1

Aby poszerzyć wiedze z tego zakresu sięgnij po książkę: John R. Taylor; Wstęp do analizy błędu pomiarowego;

PWN Warszawa 1999 i późniejsze wydania (rozdział 3).

wer. 2014 MT

5

3. Przebieg ćwiczenia

Zdj

ę

cie stanowiska przedstawiono na rysunku 2. Na stanowisku znajduje si

ę

przyrz

ą

d, który mierzy czas i jednocze

ś

nie zlicza 10 odsłoni

ęć

fotoelementu. Po

zliczeniu 10 okresów pomiar czasu automatycznie zatrzymuje si

ę

. Nale

ż

y zadba

ć

o

to aby fotoelement był odsłaniany jednokrotnie na okres ruchu tarczy. Do
przysłaniania fotoelementu słu

ż

y mała blaszka mocowana do tarczy.

Rys. 2. Stanowisko do bada

ń

momentu bezwładno

ś

ci, oraz przyrz

ą

d do pomiaru

czasu 10 wahni

ęć

tarczy

1

2

3

4

5

6

7

8

Rys.3. Warianty

ć

wiczenia

Opis kolejnych kroków, które nale

ż

y wykona

ć

, znajduje si

ę

w arkuszu sprawozdania.

Poni

ż

ej zwrócono uwag

ę

na pewne istotne zagadnienia.

1.

Ć

wiczenie mo

ż

na wykona

ć

w ró

ż

nych wariantach wyznaczaj

ą

c momenty

bezwładno

ś

ci ró

ż

nych elementów. Wariant

ć

wiczenia narzuca prowadz

ą

cy.

W poni

ż

szej tabeli przedstawiono poszczególne warianty

ć

wiczenia. Nie

zapomnij wpisa

ć

nr wariantu do arkusza sprawozdania.

2. Przy pomiarze czasu 10 –ciu wahni

ęć

samej tarczy jak i układu tarcza-element

nale

ż

y uwa

ż

a

ć

, aby maksymalny k

ą

t odchylenia tarczy nie przekraczał kilku

stopni.

3. Element nale

ż

y umie

ś

ci

ć

na tarczy w ten sposób, aby o

ś

, wzgl

ę

dem której ma

by

ć

wyznaczony moment bezwładno

ś

ci, pokrywała si

ę

z osi

ą

obrotu tarczy.

wer. 2014 MT

6

4. Zadbaj o to aby otwory w tarczy i ruchomej podstawce (pod tarcz

ą

) były

osiowe, inaczej tarcza nie b

ę

dzie obraca

ć

si

ę

swobodnie.

5. Poniewa

ż

długo

ś

ci linek mog

ą

nie by

ć

identyczne, podobnie jak odległo

ś

ci ich

zamocowania od osi tarczy, nale

ż

y odpowiednie warto

ś

ci u

ś

redni

ć

z pomiarów

wykonanych dla wszystkich trzech linek.

6. Przy analitycznych obliczeniach momentu bezwładno

ś

ci elementu skorzystaj z

pomiaru masy, wylicz przybli

ż

on

ą

obj

ę

to

ść

i nast

ę

pnie g

ę

sto

ść

materiału. W

przypadku elementów wykonanych z kilku ró

ż

nych materiałów (płytka 2 ze

zdj

ęć

powy

ż

ej) przyjmij tablicow

ą

g

ę

sto

ść

mosi

ą

dzu (tulejki) a g

ę

sto

ść

materiału samej płytki wylicz na podstawie okre

ś

lonej do

ś

wiadczalnie masy

odejmuj

ą

c mas

ę

tulejek.

7. Aby ułatwi

ć

sobie zadanie przy obliczeniach analitycznych mo

ż

esz do

pewnego stopnia upraszcza

ć

kształty elementów zast

ę

puj

ą

c je zło

ż

eniem

okre

ś

lonych brył.

8. Obliczenia przeprowad

ź

w sposób weryfikowalny tzn. wyja

ś

nij poszczególne

kroki (nazwij konkretnie to co w danym momencie obliczasz), przedstaw wzór,
podstawienie i wynik.

9. We wnioskach nale

ż

y si

ę

ustosunkowa

ć

do otrzymanych pomiarów, a w

szczególno

ś

ci ró

ż

nic pomi

ę

dzy otrzymanymi warto

ś

ciami uzyskanymi z

oblicze

ń

analitycznych oraz z eksperymentu. Przy porównaniu wyników nale

ż

y

uwzgl

ę

dni

ć

otrzymane oszacowanie niepewno

ś

ci pomiarowej. Dodatkowo

przeanalizuj jaki bł

ą

d wprowadzasz nie uwzgl

ę

dniaj

ą

c momentu bezwładno

ś

ci

małej płytki mocowanej do tarczy, słu

żą

cej do zasłonienia fotoelementu.