LABORATORIUM MECHANIKI EKSPERYMENTALNEJ

Instrukcja do ćwiczenia

RUCH PRECESYJNY GIROSKOPU

3

Cel ćwiczenia

Obserwacja zjawiska precesji regularnej. Badanie zależności prędkości kątowej precesji od momentu sił zewnętrznych.

Literatura

Do zrozumienia zjawisk giroskopowych potrzebne jest opanowanie podstawowych wiadomości z kinematyki i dynamiki ruchu kulistego ciała sztywnego. Należy zaznaczyć, że wiadomości ogólne, zawarte w niniejszej instrukcji, stanowią tylko niewielkie streszczenie teorii giroskopu. Dlatego, przed przystąpieniem do wykonywania ćwiczenia, trzeba przestudiować zagadnienie z poniżej proponowanych podręczników.

[1] J.Leyko, Mechanika ogólna, tom I, rozdz. XIV, tom II, rozdz. VII, rozdz. IX, rozdz. XII.

[2] A.Piekara, Mechanika ogólna, strony 158-167

[3] M.Łuno, A.Szaniawski, Zarys Mechaniki ogólnej, rozdz. 11, 12, 15,17, 20, 21.

[4] A.Januszajtis, Fizyka dla Politechnik, § 34, 35, 36.

[5] S.Szozeniowski, Fizyka doświadczalna, część I, rozdz; X.

Zagadnienia kontrolne

Stopień przygotowania się do ćwiczenia, pod względem opanowania potrzebnej wiedzy ogólnej, można sprawdzić, starając się odpowiedzieć na niżej podane pytania:

Co to jest ruch kulisty?

Co to jest kręt ciała (względem punktu i względem osi)?

Jaka jest treść zasady krętu?

Co to jest moment bezwładności ciała względem osi?

Co to są główne osie i główne momenty bezwładności?

Co to jest ruch precesyjny?

Co to jest precesja regularna?

Jaka jest zależność wektora prędkości kątowej precesji od wektora momentu sił

zewnętrznych?

Podstawy teoretyczne związane z przeprowadzanym eksperymentem

Giroskop to ciało sztywne, szybko wirujące dokoła swojej osi symetrii. Gdy r

moment główny M zewnętrznych sił, przyłożonych do giroskopu, jest równy zero, to na podstawie zasady krętu:

r

K

d

r

= M ,

(1)

dt

r

kręt giroskopu jest wektorem stałym ( K = const ) i oś obrotu giroskopu zachowuje swój r

kierunek w przestrzeni. Jeżeli moment główny M zewnętrznych sił nie jest równy zero, to giroskop porusza się tak, że tylko jeden jego punkt jest nieruchomy. Ruch giroskopu w tym przypadku można traktować jako ruch obrotowy dokoła osi chwilowej, przechodzącej przez ten nieruchomy punkt. Mamy tu do czynienia z ruchem kulistym giroskopu, a środek ruchu kulistego leży na osi symetrii i jest najczęściej punktem podparcia (np. przegub kulisty) giroskopu.

Równanie wektorowe (1) jest równoważne trzem równaniom skalarnym:

dK

dK

dK

x = M ,

y = M ,

z = M ,

(2)

x

dt

y

dt

z

dt

r

gdzie: M x , M , M - miary rzutów na osie układu współrzędnych momentu sił

y

M

z

zewnętrznych działających na giroskop,

r

K

K

x , K ,

- kręty względem osi x,y,z a zarazem miary rzutów krętu K na te osie.

y

z

Jeżeli osie x,y,z pokrywają się z głównymi osiami bezwładności ciała, to:

K = I ω , K = I ω , K = I ω

x

x

x

y

y

y

z

z

z

gdzie: I

ω ω ω

x , Iy, Iz - są głównymi momentami bezwładności ciała, a x ,

y ,

z to

składowe chwilowej prędkości kątowej ωr względem głównych osi bezwładności.

Oczywiście, jeśli:

ω ≠ ω

ω ≠ ω

ω ≠ ω

x

y

y

z

x

z

I ≠ I

I ≠ I

I ≠ I

x

y

x

z

y

z

to kierunek osi chwilowej, zgodny z kierunkiem wektora ωr , nie pokrywa się z żadną z r

głównych osi bezwładności ciała i nie pokrywa się także z kierunkiem K krętu ciała.

Dlatego w giroskopie, znajdującym się pod działaniem momentu sił zewnętrznych, konieczne jest rozróżnienie trzech prostych, przechodzących przez nieruchomy punkt (punkt podparcia giroskopu), a mianowicie:

1. kierunek chwilowej prędkości kątowej ω

r

,

r

2. kierunek krętu K ,

3. kierunek osi symetrii giroskopu.

Pierwsze dwa kierunki są niewidoczne w czasie ruchu giroskopu i zmieniają się w przestrzeni oraz względem samego giroskopu. Oś symetrii giroskopu jest widoczna i w czasie ruchu giroskopu zmienia swoje położenie tylko względem otaczającej przestrzeni.

W przybliżonej, elementarnej teorii ruchu giroskopu zakłada się, że kierunki r

wektorów K i ω

r

mało się różnią od kierunku osi symetrii i to w dowolnej chwili. Tak jest wtedy, gdy giroskop szybko obraca się dokoła osi symetrii pokrywającej się, np. z osią x. Wtedy:

ω >> ω , ω

>> ω

x

y

x

z

zatem, ω

r

ma kierunek mało różniący się od kierunku osi symetrii. Ponieważ Ix , Iy, Iz są tego samego rzędu i zazwyczaj:

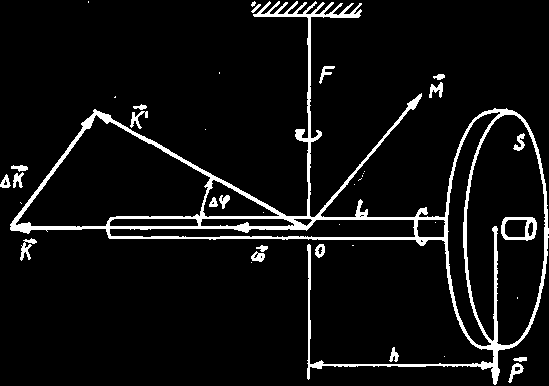
I > I , I > I ,

x

y

x

z

r

to kierunek K będzi

z e

i blils

i ki

i kie

i ru

r nkowi

w

i osi

i x. Przy bard

r zo szybkim

i wi

w ro

r wa

w niu

gir

i o

r skopu dokoła

ł osi sym

y etriii we

w ktor

r chwilowej prędkości kątowe

w j

j i

i we

w kt

k o

t r

r krętu

prawie leżą na osi symetri

r ii.

i Dlatego można wnioskować o

o ruc

u h

c u

h

u chw

h ilow

o ej

j os

o i

obrotu obserwując ruc

u h

h os

o i sym

y etr

t ii giros

o kop

o u. Gdy

y nie

i ma momentu sił

r

r

r

zewnętrznych ( M =0),

) to

t

o z

z ró

r wnania (1) otrzymujemy: K = co

c n

o s

n t. Wtedy kręt K ,

prędkość kątowa ω

r

i oś

ś sy

s m

y e

m t

e r

t i

r ii

i gi

g r

i o

r s

o k

s o

k p

o u

p

u pozostają w

w pr

p z

r e

z s

e t

s r

t z

r e

z n

e i

n

i ni

n e

i r

e u

r c

u h

c o

h me i stałe

co do wielkości.

Dl

D a

l kró

r tk

t ot

o rw

r a

w łe

ł go

g dzi

z a

i ła

ł n

a ia

i si

s łi

ł ze

z wn

w ętr

t z

r n

z yc

y h (u

( d

u e

d rz

r e

z n

e ie

i )

) cza

z s ∆t jest bardzo

ma

m ł

a y

ł ,

y

, d

l

d a

l t

a e

t g

e o

g

o (

r

( ó

r w

ó n

w a

n n

a i

n e

i

e (

1

( )

1 )

)

) b

ędzie bardzo mały przyrost krętu:

r

r

∆ K = M t

∆

(3)

r

stąd małe będą zm

z ia

i n

a y

n

y kie

i ru

r nków

w w

w prze

z strz

r eni

i we

w ktoró

r w

w K i ω

r

i

i osi

i symetrii .

Gdy zewnętr

t z

r n

z e

n

e si

s łiy

ł

y dz

d i

z a

i ł

a a

ł j

a ą dł

d u

ł g

u o

g ,

o

, na

n we

w t

e

t wt

w e

t dy

d ,

y

, gd

g y

y ic

i h

c

h mo

m m

o e

m n

e t

n

t je

j s

e t

s

t niewielki,

r

kie

i r

e u

r n

u e

n k

k w

w prz

r e

z st

s rz

r e

z n

e i

n

i we

w kto

t ra

r K i wektora ω

r

i kierunek osi symetrii będą się

zmieniać. Ta

T k

a i

k

i r

u

r c

u h

c

h n

a

n z

a y

z w

y a

w

a s

i

s ę precesją.

Ni

N e

i ch giro

r skop ma postać je

j dnoro

r dnej

j tarc

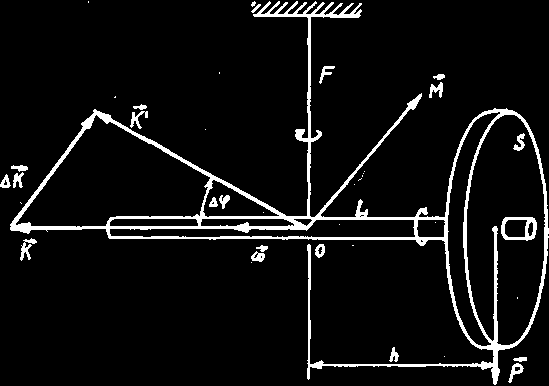
r zy S (rys.1) szybko obracającej się

na pręci

c e

i

e L

L za

z w

a i

w e

i s

e z

s o

z n

o y

n m

y

m na

n

a ni

n c

i i

c

i F.

F

. Gd

G y

d

y na

n d

a a

d m

a y

m

y gi

g r

i o

r s

o k

s o

k p

o o

p w

o i

w

i ob

o ro

r t

o y

t

y i

i us

u t

s a

t w

a i

w m

i y

m

y je

j g

e o

g

o oś

poziomo, to zacznie się

ę on

o a

n

a ob

o r

b a

r c

a a

c ć w płaszczyźnie

i pozi

z o

i mej

e

j dokoła punktu

r

za

z wi

w e

i sze

z nia

i O. W om

o awi

w a

i nym

y prz

r yp

y adku

u na gi

g roskop działa moment M siły

r

ciężkości P (np. ciężar silniczka):

M = P ⋅ h

(4)

h jest odległością od punktu O do środka ciężkości giroskopu, a M modułem wektora momentu .

Rys.1.

r

Moment M jest prostopadły do płaszczyzny rysunku i skierowany od oczu patrzącego na rysunek. Jeżeli tarcza giroskopu szybko obraca się tak, jak zaznaczono na rysunku, to wektor

r

r

r

K′ = K + K

∆

r

tworzy kąt ϕ

∆ z wektorem K . Kąt ϕ

∆ leży w płaszczyźnie poziomej.

Wymuszony ruch giroskopu będzie odbywał się w płaszczyźnie poziomej, zgodnie z ruchem wskazówek zegara, jeśli patrzy się z góry. Łatwo sprawdzić, że gdy zmieni się kierunek obrotów tarczy giroskopu, płaszczyzna obrotu osi giroskopu pozostanie ta sama ale kierunek obracania osi będzie odwrotny, niż poprzednio. Kierunki odpowiednich wektorów są znane i dalej rozpatrywane będą tylko ich wartości.

Niech Ω oznacza prędkość kątową procesji, tzn. prędkość obracania się osi giroskopu pod działaniem stałego momentu sił zewnętrznych. W czasie ∆t przyrost krętu (rys.1) będzie wynosił:

∆

K

∆

∆ϕ

K = K ⋅ ϕ

∆

stąd

= K ⋅

.

t

∆

∆ t

Przechodząc do granicy, gdy ∆t->0, otrzymujemy:

dK

dϕ

= K ⋅

(5)

dt

dt

Prędkość kątowa precesji wynosi:

dϕ

Ω =

dt

dK

Ponieważ

= M i K = ω

I , ze wzoru (5) otrzymamy:

dt

dK

d

=

ϕ

K

= KΩ = M , M = Ω

ω

I

(6)

dt

dt

Przebieg ćwiczenia

Celem wykonywanych pomiarów jest wyznaczenie prędkości obrotowej wirnika giroskopu na podstawie wyprowadzonych zależności.

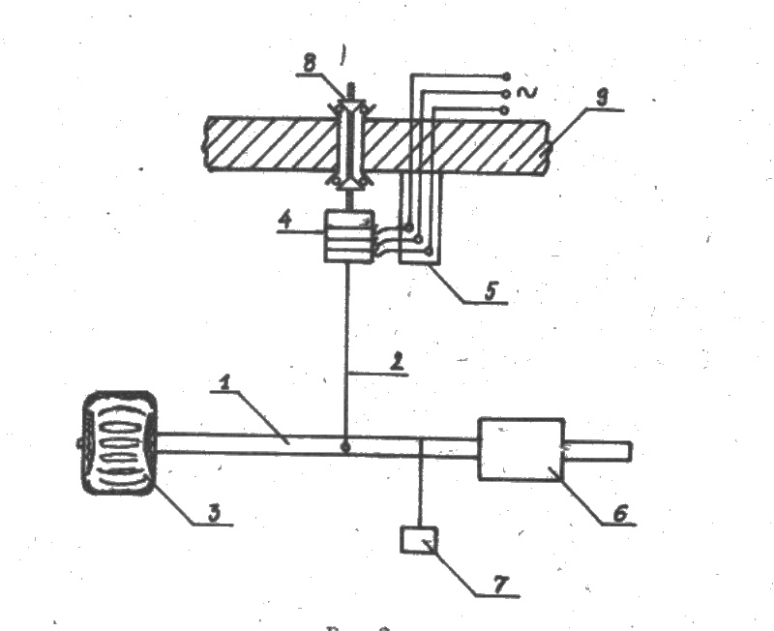
Przyrząd składa się z metalowego pręta (1) (rys.2) zawieszonego przegubowo na pionowym wałku (2) . Pręt (1) może obracać się dokoła osi poziomej i pionowej, które przechodzą przez jego środek. Na jednym końcu pręta jest umocowany silniczek (3).

Silniczek ten jest zasilany prądem trójfazowym (400 Hz, 36 V) poprzez trzy pierścienie (4) i blaszki kontaktowe (5). Zasilacz znajduje się w podstawie przyrządu.

Wirnik silniczka, obracając się z dużą prędkością kątową, jest właśnie giroskopem.

Na drugim ramieniu pręta (1) umieszcza się przeciw-wagę (6) silnika; jej położenie dobiera się tak, aby pręt (1) pozostawał w pozycji poziomej. Dodatkowy ciężarek (7) wytwarza moment siły zewnętrznej, wywołujący ruch precesyjny. Dla małego momentu będzie mała prędkość kątowa Ω precesji, a czas pełnego obrotu osi giroskopu będzie znaczny. W tym czasie może ujawnić się działanie momentu sił

tarcia w zawieszaniu (8) wałka (2) na belce (9); giroskop będzie w precesji także dokoła osi poziomej poprzecznej do pręta (1). Dlatego w zawieszeniu (8) powinny być dobre łożyska poprzeczno-wzdłużne. Wtedy, dla dwóch lub trzech obrotów precesyjnych, kąt między prętem (1) i pionem pozostanie, w przybliżeniu, prostym.

Rys.2.

Na wstępie, trzeba sprawdzić, czy pręt (1) może swobodnie obracać się dokoła pionowej i poziomej osi. Następnie ustala się położenie przeciwwagi (6) tak, aby pręt (1) pozostał w pozycji poziomej. Po włączeniu prądu, należy odczekać około 10

minut, aż wirnik silnika uzyska maksymalne obroty. Gdy silnik zacznie pracować na maksymalnych obrotach, przytrzymujemy pręt (1) i zawieszamy dodatkowy ciężarek (7). Wtedy ostrożnie puszcza się giroskop; rozpocznie się ruch precesyjny. Przy pomocy sekundomierza wyznacza się okres T pełnego obrotu precesyjnego giroskopu. Stąd prędkość kątowa precesji:

π

2

Ω =

(7 )

T

Ta prędkość odpowiada momentowi M, wytworzonemu przez ciężarek (7). Należy wyznaczyć prędkość kątową precesji dla różnych wartości momentu M, zmieniając wielkość i ramię siły ciężkości ciężarka (7).

Znając prędkość kątową precesji dla zadanego momentu siły można wyznaczyć prędkość kątową wirnika giroskopu ω z zależności:

M = Iω Ω

Należy przyjąć, że moment bezwładności wirnika giroskopu wynosi:

I = (168

, ± 0

,

1 )

5

−

2

⋅10 k gm

Po wykonaniu zadanej liczby pomiarów należy wyłączyć zasilanie silnika.

Okres ruchu precesyjnego dla niewielkich momentów siły może być bardzo długi. Z

powodu sił tarcia nie uda się wtedy zmierzyć nawet całego okresu ruchu. Należy tak dobrać masę ciężarka i ramię siły aby móc zmierzyć jeden okres ruchu.

Szczegółowe kroki przeprowadzonych pomiarów i sposób obliczenia wyników znajdują się w arkuszu sprawozdania.