1. Dane ogólne

1.1. Podstawy opracowania
[1] Rozp MTiGM z dnia 2-03-1999r w sprawie warunków technicznych, jakim powinny odpowiadać
drogi publiczne i ich usytuowanie (Dz. U. Nr 43 z 1999 r.)
[2] Rozp MTiGM z dnia 30-05-2000r w sprawie warunków technicznych, jakim powinny
odpowiadać drogowe obiekty inżynierskie i ich usytuowanie (Dz. U. Nr 63 z 2000 r.)
[3] PN-EN 1990:2004
[4] PN-EN 1991-1-1:2004

[5] PN-EN 1991-2:2003

[6] PN-EN 1992-1-1:2008

[7] PN-EN 1993-1-1:2006

[8] PN-EN 1993-1-5:2008
[9] PN-EN 1993-1-8:2006

[10] PN-EN 1994-1-1:2008

[11] PN-EN 1994-2:2010

Podstawy projektowania konstrukcji
Oddziaływania na konstrukcje - Część 1-1: Oddziaływania ogólne -
ciężar objętościowy, ciężar własny, obciążenia użytkowe w
budynków
Oddziaływanie na konstrukcje. Część 2: Obciążenia ruchome
mostów
Projektowanie konstrukcji z betonu. Część 1-1: Reguły ogólne i
reduły dla budynków.
Projektowanie konstrukcji z stalowych. Część 1-1: Reguły ogólne i
reduły dla budynków.
Projektowanie konstrukcji stalowych. Część 5: Blachownice.
Projektowanie konstrukcji stalowych. Część 8: Projektowanie
węzłów.
Projektowanie konstrukcji zespolonych stalowo-betonowych. Część
1-1: Reguły ogólne i reguły dla budynków.
Projektowanie konstrukcji zespolonych stalowo-betonowych.
Część 2: Reguły ogólne i reguły dla mostów.

1.2. Opis projektowanego mostu

Zaprojektowano most stały jednoprzęsłowy, zlokalizowany nad rzeką w spadku podłużnym

0,5%. Ustrój niosący wolnopodparty rozpiętości .... , o konstrukcji stalowej zespolonej z płytą
żelbetową monolityczną. Rusz stalowy składa się z .... belek stalowych o wysokości ..... w rozstawie
.... . Płyta żelbetowa grubości .... zespolona z belkami przy użyciu bolców stalowych. Przyczółki
monolityczne żelbetowe ze skrzydłami wolnostojącymi posadowione na wspólnej ławie żelbetowej.
Ława żelbetowa na ruszcie z pali wierconych o średnicy .... .

1.3. Parametry techniczno-użytkowe:
Po wybudowaniu obiekt będzie posiadał następujące parametry techniczno-użytkowe:
-długość całkowita ustroju niosącego 00,00 m
-rozpiętość teoretyczna przęsła 18,00 m
-światło poziome 00,00 m
-szerokość konstrukcyjna mostu 9,04 m
-elementy drogi na moście:
- jezdnia w krawężnikach 6,00 m
-szerokość użytkowa w świetle barier 6,50 m
-chodnik jednostronny 1,00 m
-obciążenie mostu:
-LM1 wg PN-EN 1991-2:2003 Oddziaływanie na kostrukcje. Część 2: Obciążenia ruchome mostów

1.4. Cechy materiałowe elementów konstrukcyjnych:

Beton C 30/37
Stal konstrukcyjna S420

1

1.4.1 Wytrzymałość betonu:

γc

1.40



-współczynnik częściowy bezpieczeństwa:

-współczynnik uwzględniający efekty długotrwałych oraz niekorzystnych
wpływów, wynikających ze sposobu przyłożenia obciążenia:

-wytrzymałość charakterystyczna przy osiowym ściskaniu:

-wytrzymałość obliczeniowa przy osiowym ściskaniu:

-wytrzymałość średnia przy osiowym ściskaniu:

-współczynnik sprężystości podłużnej betonu:

αcc

1.00



fck

30 MPa





fcd

αcc

fck

γc





fcd 21.43 MPa





fcm 38 MPa





Ecm 32 GPa





1.4.2 Wytrzymałość stali:
-współczynnik częściowy bezpieczeństwa:

-współczynnik częściowy stosowany przy sprawdzeniu
nośności przekroju poprzecznego:

-współczynnik częściowy stosowany przy sprawdzeniu
stateczności elementu:

-współczynnik częściowy stosowany przy sprawdzeniu
nośności przekroju na rozerwanie:

-współczynnik sprężystości podłużnej stali:

-wytrzymałość charakterystyczna:

-wytrzymałość obliczeniowa:

-wytrzymałość obliczeniowa na rozciąganie:

-wytrzymałość obliczeniowa na ściskanie:

γs

1.15



γMO

1.00



γM1

1.10



γM2

1.25



Es

210 GPa





fyk

420 MPa





fyd

fyk

γs



fyd 365 MPa





fu

520 MPa





ft fu 0.6





ft 312 MPa





2

2. Zebranie obciążeń działających na most
2.1 Dane wstępne

b

kc

b

n

b

kg

b

c

b

z

a/b

w

a/b

w

a/b

w

a/b

w

b

z

b

d

b

i

t

f

h

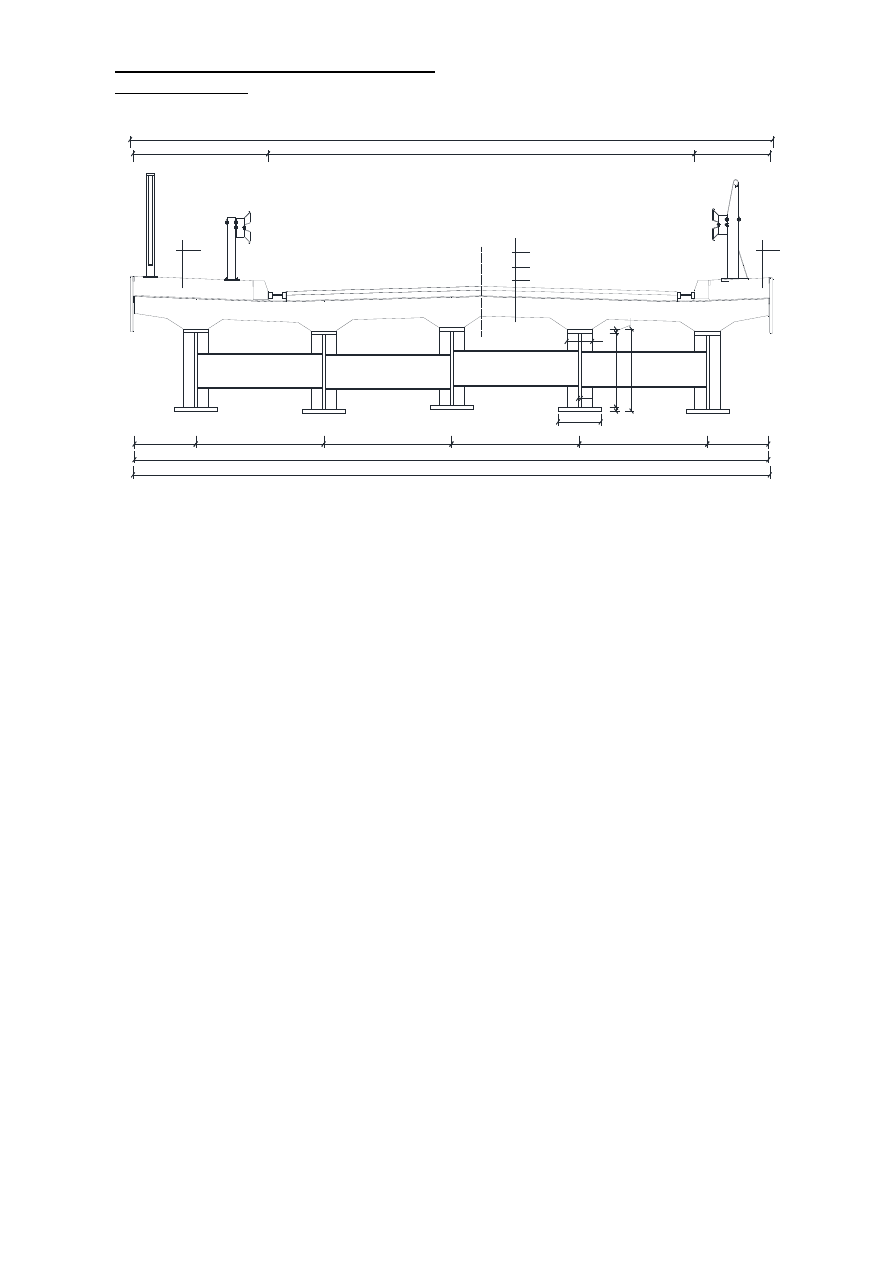
Rys. 1. Przekrój poprzeczny rozpatrywanego mostu

b

f

t

w

b

t

t

f

h

w

h

kc

h

kg

h

n

h

i

h

d

-długość całkowita przęsła:

-rozpiętość teoretyczna przęsła:

-szerokość całkowita obiektu:

-rozstaw dźwigarów:

-szerokość kapy chodnikowej:

-szerokość kapy gzymsowej:

-szerokość jezdni:

-szerokość izolacji:

-grubość kapy chodnikowej:

-grubość kapy gzymsowej:

L

37.14 m





Lt 18.00 m





bc

9.04 m





a

1.80 m





bkc

1.94 m





bkg

1.10 m





bn

6.00 m





bi 8.96 m





hkc

0.225 m





hkg

0.225 m





-grubość jezdni:

-grubość izolacji:

-szerokość wewnętrzna płyty:

-szerokość zewnętrzna płyty:

hn

0.10 m





hi 0.005 m





bw

1.80 m





bz

0.86 m





bd

8.92 m





-szerokość całkowita płyty:

-grubość płyty:

-grubość skosu płyty:

hd

0.21 m





hp

0.12 m





3

-szerokość skosu płyty:

-szerokość pasa górnego:

-grubość pasa górnego:

-wysokość środnika:

-grubość środnika:

-szerokość pasa dolnego:

-grubość pasa dolnego:

-wysokość całkowita blachownicy:

bp

0.216 m





bt 0.36 m





tt 0.02 m





hw

1.2 m





tw

0.011 m





bf

0.48 m





tf

0.04 m





h

1.26 m





2.2. Zestawienie obciążeń

Przyjęte kombinacje obciążeń w stanie granicznej nośności (STR/GEO):

j 1



γG.j Gk.j



γP P





γQ.1 Qk.1











i 1



γQ.i ψ0.i



Qk.i











i w stanie granicznej użytkowalności (kombinacja charakterystyczna):

j 1



Gk.j



P



Qk.1



i 1



ψ0.i Qk.i











W obliczeniach uwzględnia się obciążenie stałe, obciązenie ruchome w postaci taboru na jezdni (LM1)
i ciężar pieszych na chodniku. Rozpatrywana jest kombinacja obciążeń zmiennych z grupy "gr1a":

-współczynnik częściowy oddziałwań stałych:

-współczynnik częściowy oddziaływań zmiennych wiodących (LM1)
oraz zmiennych towarzyszących (piesi):

-współczynnik redukcyjny oddziaływań zmiennych towarzyszących
(wartość kombinacyjna):

-współczynniki korekcyjne oddziaływań zmiennych wiodących (LM1):

γG.j.sup

1.35



γG.j.inf

1.00



γQ

1.35



ψ0

0.40



αQ

1.00



αq

1.00



αq.r

1.00



4

Obciążenia stałe
W obliczeniach pominięto ciężar deskowania w Fazie I oraz ujemny ciężar usuniętego deskowania i
ujemny ciężar zmniejszenia ciężaru objętościowego betonu płyty w skutek odparowania części wody
zarobowej w Fazie II.

L.p. Nazwa elementów obciążenia

Ciężar objetośc.

Lub liniowy (r

i

)

Jednostki

ciężaru

Obciążenie

charakterystyczne

Jednostki

obciążeń

1.

W arstwy nawierzchni

(h

n

x r

i

)

25

kN/m

3

2,50

kN/m

2

2.

Izolacja płyty pomostu

(h

i

x r

i

)

14

kN/m

3

0,07

kN/m

2

3.

Kapa chodnikowa z

krawężnikiem (h

kc

x r

i

)

27

kN/m

3

6,08

kN/m

2

4.

Kapa gzymsowa z

krawężnikiem (h

kg

x r

i

)

27

kN/m

3

6,08

kN/m

2

5.

Deska gzymsowa

0,1

kN/mb

0,10

kN/mb

6.

Balustrada aluminiowa

0,4

kN/mb

0,40

kN/mb

7.

Bariera mostowa

0,5

kN/mb

0,50

kN/mb

8.

Barieroporęcz mostowa

0,8

kN/mb

0,80

kN/mb

9.

Płyta pomostu

(h

d

x r

i

)

26

kN/m

3

5,46

kN/m

2

Blachownica

[(b

t

x t

t

+ h

w

x t

w

+ b

f

x t

f

) x r

i

]

78,5

kN/m

3

3,11

kN/mb

Łączniki i stężenia

1

kN.mb

1,00

kN/mb

4,11

kN/mb

10.

Razem:

Obciążenie zmienne wiodące - obciążenie ruchome model LM1
układ tandemowy TS:

układ UDL:

Pas nr 1 (nacisk na oś)

Pas nr 2 (nacisk na oś)

Pas nr 1

Pas nr 2

Q1k

600 kN





Q2k

400 kN





q1k

9.00

kN

m

2





q2k

2.5

kN

m

2





Obciążenie zmienne towarzyszące - obciążenie ruchome tłum
pieszych na chodniku

Szerokość użytkowa chodnika

qfk

5.00

kN

m

2





5

2.3. Rozkład poprzeczny obciążeń ( metoda sztywnej poprzecznicy )
2.3.1. Wyznaczenie linii wpływu umownej reakcji w dźwigarze
Rzędna linii wpływu dla k-tego dźwigara od siły jednostkowej:

η

1
k

x bi



Σ

bi

2



=

gdzie:
η - rzędna linii wpływu rozkładu poprzecznego
k - liczba dźwigarów
b

i

- odległość i-tego dźwigara od osi poprzecznej mostu

x - odległośc od osi przekroju poprzecznego mostu, szukanej rzędnej linii wpływu

Sumaryczna reakcja w dźwigarze przyskrajnym od siły jednostkowej

ηs

1
k

x bps



Σ

bi

2



=

k

5



b1

3.6 m





b3

0 m





b5

3.6



m





bps

1.8 m





b2

1.8 m





b4

1.8



m





bs

b1 3.6m





Wyznaczenie przebiegu funkcji (*):

- rzędna q.dglk

xdglk 4.48 m





ηdglk

1
5

xdglk 1.8



m

3.6m

(

)

2

1.8m

(

)

2



0m

(

)

2



1.8



m

(

)

2



3.6



m

(

)

2







ηdglk 0.449



- rzędna q.balk

xbalk

4.24 m





ηbalk

1
k

xbalk bps



2

b1

 

2

b2

 

2

















ηbalk

0.436



- rzędna q.fk

xfk 3.69 m





ηfk

1
k

xfk bps



2

b1

 

2

b2

 

2

















ηfk

0.405



- rzędna dźwigara 1 x1 b1



ηb1

1
k

x1 bps



2

b1

 

2

b2

 

2

















ηb1

0.4



- rzędna q.bak

xbak

3.1 m





ηbak

1
k

xbak bps



2

b1

 

2

b2

 

2

















ηbak

0.372



6

- rzędna K.I

xKI

2.58 m





ηKI

1
k

xKI bps



2

b1

 

2

b2

 

2

















ηKI

0.343



- rzędna Q.11k

x11k

2.08 m





η11k

1
k

x11k bps



2

b1

 

2

b2

 

2

















η11k

0.316



- rzędna dźwigara 2 x2 b2



ηb2

1
k

x2 bps



2

b1

 

2

b2

 

2

















ηb2

0.3



- rzędna q.1k

x1k

1.08 m





η1k

1
k

x1k bps



2

b1

 

2

b2

 

2

















η1k

0.26



- rzędna Q.12k

x12k

0.08 m





η12k

1
k

x12k bps



2

b1

 

2

b2

 

2

















η12k

0.204



- rzędna dźwigara 3 x3 b3



ηb3

1
k

x3 bps



2

b1

 

2

b2

 

2

















ηb3

0.2



- rzędna Q.21k

x21k

0.92



m





η21k

1
k

x21k bps



2

b1

 

2

b2

 

2

















η21k

0.149



- rzędna q.2k

x2k

1.92



m





η2k

1
k

x2k bps



2

b1

 

2

b2

 

2

















η2k

0.093



7

- rzędna dźwigara 4 x4 b4



ηb4

1
k

x4 bps



2

b1

 

2

b2

 

2

















ηb4

0.1



- rzędna Q.22k

x22k

2.92



m





η22k

1
k

x22k bps



2

b1

 

2

b2

 

2

















η22k

0.038



- położenie jednostkowej, przy którym wartość umowna reakcji w dźwigarze przyskrajnym jest
zerowa

ηS

0



x0

1



k

2

b1

 

2

b2

 

2













bps





x0

3.6



m



- rzędna dźwigara 5 x5 b5



ηb5

1
k

x5 bps



2

b1

 

2

b2

 

2

















ηb5

0



- rzędna K.p

xKp

3.42



m





ηKp

1
k

xKp bps



2

b1

 

2

b2

 

2

















ηKp

0.01



- rzędna q.bmk

xbmk

4.00



m





ηbmk

1
k

xbmk bps



2

b1

 

2

b2

 

2

















ηbmk

0.022





- rzędna q,dgpk

xdgpk

4.48



m





ηdgpk

1
k

xdgpk bps



2

b1

 

2

b2

 

2

















ηdgpk

0.049





Sumaryczna reakcja w dźwigarze skrajnym od siły jednostkowej

ηs

1
k

x bps



Σ

bi

2



=

Wyznaczenie przebiegu funkcji (*):
- rzędna q.dglk

xdglk 4.48 m





ηdglk

1
5

xdglk 3.6



m

3.6m

(

)

2

1.8m

(

)

2



0m

(

)

2



1.8



m

(

)

2



3.6



m

(

)

2







ηdglk 0.698



8

- rzędna q.balk

xbalk

4.24 m





ηbalk

1
k

xbalk bs



2

b1

 

2

b2

 

2

















ηbalk

0.671



- rzędna q.fk

xfk 3.69 m





ηfk

1
k

xfk bs



2

b1

 

2

b2

 

2

















ηfk

0.61



- rzędna dźwigara 1 x1 b1



ηb1

1
k

x1 bs



2

b1

 

2

b2

 

2

















ηb1

0.6



- rzędna q.bak

xbak

3.1 m





ηbak

1
k

xbak bs



2

b1

 

2

b2

 

2

















ηbak

0.544



- rzędna K.I

xKI

2.58 m





ηKI

1
k

xKI bs



2

b1

 

2

b2

 

2

















ηKI

0.487



- rzędna Q.11k

x11k

2.08 m





η11k

1
k

x11k bs



2

b1

 

2

b2

 

2

















η11k

0.431



- rzędna dźwigara 2 x2 b2



ηb2

1
k

x2 bs



2

b1

 

2

b2

 

2

















ηb2

0.4



- rzędna q.1k

x1k

1.08 m





η1k

1
k

x1k bs



2

b1

 

2

b2

 

2

















η1k

0.32



- rzędna Q.12k

x12k

0.08 m





η12k

1
k

x12k bs



2

b1

 

2

b2

 

2

















η12k

0.209



9

- rzędna dźwigara 3 x3 b3



ηb3

1
k

x3 bs



2

b1

 

2

b2

 

2

















ηb3

0.2



- rzędna Q.21k

x21k

0.92



m





η21k

1
k

x21k bs



2

b1

 

2

b2

 

2

















η21k

0.098



- rzędna q.2k

x2k

1.11



m





η2k

1
k

x2k bs



2

b1

 

2

b2

 

2

















η2k

0.077



- położenie jednostkowej, przy którym wartość umowna reakcji w dźwigarze skrajnym jest zerowa

ηS

0



x0

1



k

2

b1

 

2

b2

 

2













bs





x0

1.8



m



- rzędna dźwigara 4

x4

b4



ηb4

1
k

x4 bs



2

b1

 

2

b2

 

2

















ηb4

0



- rzędna dźwigara 5 x5 b5



ηb5

1
k

x5 bs



2

b1

 

2

b2

 

2

















ηb5

0.2





- rzędna K.p

xKp

3.42



m





ηKp

1
k

xKp bs



2

b1

 

2

b2

 

2

















ηKp

0.18





- rzędna q.bmk

xbmk

4.00



m





ηbmk

1
k

xbmk bs



2

b1

 

2

b2

 

2

















ηbmk

0.244





- rzędna q.dgpk

xdgpk

4.48



m





ηdgpk

1
k

xdgpk bs



2

b1

 

2

b2

 

2

















ηdgpk

0.298





10

Obciążenie ruchome, które zlokalizowane jest na ujemnej gałęzi linii wpływu nie jest uwzględniane w
obliczeniach.
W związku z tym:
* wartość obciążenia występującego tylko w przypadku wyznaczania linii wpływu dźwigara
skrajnego
**wartość obciążenia występującego tylko w przypadku wyznaczania linii wpływu dźwigara
przyskrajnego

Pole powierzchni dodatniej linii wpływu:

As

1
2

0.689



m

 6.28



m



2.163 m

2





Aps

1
2

0.449



m

 8.08



m



1.814 m

2





- dźwigara skrajnego

As Aps



1



- dźwigara przyskrajnego

Z uwagi na to, że wszystkie rzędne linii wpływu dźwigara skrajnego oraz pole powierzchni dodatniej
części są większe od analogicznych wartości w przypadku dźwigara przyskrajnego, dalsze obliczenia
będą prowadzone dla dźwigara skrajnego.
2.3.1. Wyznaczenie obciążeń przypadających na dźwigar

Obciążenia stałe (wartości charakterystyczne i obliczeniowe)



- blachownica z łącznikami i stężeniami:

qbk

4.11

kN

m

ηb1 ηb2



ηb3



ηb4



ηb5











qbk 4.11

kN

m





qbd

4.11

kN

m

ηb1 γG.j.sup



ηb2 γG.j.sup





ηb3 γG.j.sup





ηb4 γG.j.inf



ηb5 γG.j.inf























qbd 5.836

kN

m





- płyta pomostu:

qdk

5.46

kN

m

2

ηdglk xdglk x0









2

ηdgpk x0 xdgpk









2



















qdk 9.784

kN

m





qdd

5.46

kN

m

2

ηdglk xdglk x0









2

γG.j.sup



ηdgpk x0 xdgpk









2

γG.j.inf































qdd 13.971

kN

m





- warstwy nawierzchni:

qwk

2.5

kN

m

2

ηKI xKI x0









2

ηKp x0 xKp









2



















qwk 2.3

kN

m





qwd

2.5

kN

m

2

ηKI xKI x0









2

γG.j.sup



ηKp x0 xKp









2

γG.j.inf































qwd 3.233

kN

m





11

- izolacja płyty pomostu:

qik 0.07

kN

m

2

ηdglk xdglk x0









2

ηdgpk x0 xdgpk









2



















qik 0.125

kN

m





qid 0.07

kN

m

2

ηdglk xdglk x0









2

γG.j.sup



ηdgpk x0 xdgpk









2

γG.j.inf































qid 0.179

kN

m





- kapa chodnikowa z krawężnikiem:

qkck

6.08

kN

m

2

ηdglk ηKI







xdglk xKI









2

ηKI xdglk xKI



























qkck 6.841

kN

m





qkcd

6.08

kN

m

2

ηdglk ηKI







xdglk xKI









2

ηKI xdglk xKI































γG.j.sup





qkcd 9.236

kN

m





- kapa gzymsowa z krawężnikiem:

qkgk

6.08

kN

m

2

ηKp xKp xdgpk









ηdgpk ηKp







xKp xdgpk









2



















qkgk

1.54



kN

m





qkgd

6.08

kN

m

2

ηKp xKp xdgpk









ηdgpk ηKp







xKp xdgpk









2























γG.j.inf





qkgd

1.54



kN

m





- deska gzymsowa:

qdgk

0.10

kN

m

ηdglk ηdgpk











qdgk 0.04

kN

m





qdgd

0.10

kN

m

ηdglk γG.j.sup



ηdgpk γG.j.inf













qdgd 0.064

kN

m





- balustrada aluminiowa:

qbalk

0.40

kN

m

ηbalk









qbalk 0.268

kN

m





qbald

0.40

kN

m

ηbalk







γG.j.sup





qbald 0.362

kN

m





- balustrada mostowa:

qbak

0.50

kN

m

ηbak

 





qbak 0.272

kN

m





qbad

0.50

kN

m

ηbak

 



γG.j.sup





qbad 0.367

kN

m





12

- barieroporęcz mostowa:

qbmk 0.80

kN

m

ηbmk









qbmk

0.196



kN

m





qbmd 0.80

kN

m

ηbmk







γG.j.sup





qbmd

0.264



kN

m





Obciążenie zmienne (wartości charakterystyczne i obliczeniowe):



- układ tandemowy TS:

Qk

300kN η11k η12k









200kN η21k







Qk 211.556 kN





Qd

300kN η11k γQ



αQ



η12k γQ αQ

















200kN η21k



γQ αQ













Qd 285.6 kN





- układ UDL i obciążenie tłumem pieszych:

qk

27

kN

m

η1k



3.35

kN

m

η2k





5

kN

m

ηfk







qk 11.947

kN

m





qd

27

kN

m

η1k



γQ



αQ



3.35

kN

m

η2k



γQ



αQ





5

kN

m

ηfk



γQ



αQ







qd 16.128

kN

m





2.4. Wyznaczenie sił wewnętrznych
Wyznaczone wartości obciążeń ustawiamy na myślowo wyjętym z ustroju nośnego dźwigarze skrajnym

Faza I



- blachownica z łącznikami, stężeniami i płytą pomostu:

(moment zg.) ->

Msk.I

qbk qdk







Lt

2



8



Msk.I 562.72 kN m







(siła tnąca) ->

Tsk.I

qbk qdk







Lt



2



Tsk.I 125.049 kN





(moment zg.) ->

Msd.I

qbd qdd







Lt

2



8



Msd.I 802.206 kN m







(siła tnąca) ->

Tsd.I

qbd qdd







Lt



2



Tsd.I 178.268 kN





Faza II



- elementy wyposażenia:

Msk.II

qwk qik



qkck



qkgk



qdgk



qbalk



qbak



qbmk







Lt

2



8



Msk.II 328.549 kN m







Tsk.II

qwk qik



qkck



qkgk



qdgk



qbalk



qbak



qbmk







Lt



2



Tsk.II 73.011 kN





Msd.II

qwd qid



qkcd



qkgd



qdgd



qbald



qbad



qbmd







Lt

2



8



Msd.II 471.349 kN m







Tsd.II

qwd qid



qkcd



qkgd



qdgd



qbald



qbad



qbmd







Lt



2



Tsd.II 104.744 kN





13

- obciążenia ruchome:

Mrk.II

qk

Lt

2

8



Qk

Lt

4







Mrk.II 1435.847 kN m







Trk.II

qk

Lt

2



Qk

1
2







Trk.II 213.299 kN





Mrd.II

qd

Lt

2

8



Qd

Lt

4







Mrd.II 1938.393 kN m







Trd.II

qd

Lt

2



Qd

1
2







Trd.II 287.954 kN





3. Wymiarowanie dźwigara głównego
3.1. Wyznaczanie naprężeń normalnych od obciążeń stałych i ruchomych

UWAGA!!!!!

Szerokość współpracującą półki należy wyznaczyć wg PN-EN 1994-2 pkt 5.4.1.2 (patrz pomoce
03.Szerokość współpracująca płyty beff)

Charakterystyki geometryczne przekroju stalowego - Faza I



- pole powierzchni przekroju stalowego:

As

bt tt



hw tw





bf tf







As 0.0396m

2



- moment statyczny przekroju stalowego względem krawędzi półki dolnej:

Ss

bt tt



tt
2

hw



tf

















hw tw



hw

2

tf



















bf tf



tf

2







Ss 0.017832 m

3





14

- środek ciężkości przekroju stalowego:

ysd

Ss

As



ysd 0.4503m



ysg

h ysd





ysg 0.8097m



- moment bezwładności przekroju stalowego względem własnej osi ciężkości:

Js

bt tt

3



12

bt tt



ysg

tt
2















2





tw hw

3



12



tw hw



ysg

hw

2



tt















2





bf tf

3



12

bf tf



ysd

tf

2















2











Js 0.010221m

4



Charakterystyki geometryczne przekroju zespolonego - Faza II



- pole powierzchni przekroju betonowego:

Ac

beff hd



2 bp



bt







bt



2













hp







Ac 0.4391m

2



- moment statyczny przekroju betonowego względem górnej krawędzi płyty:

Sc

beff hd



hd

2



bt hp



hd

hp

2



















2

bp hp



2

hd

hp

3



































Sc 0.056996 m

3





- środek ciężkości przekroju betonowego:

ycg

Sc

Ac



ycg 0.1298m



ycd

hd hp







ycg





ycd 0.2002m



- moment bezwładności przekroju betonowego względem własnej osi ciężkości:

Jc

beff hd

3



12

beff hd



ycg

hd

2















2





bt hp

3



12



bt hp



hp

2

hd



ycg















2





2

bp hp

3



36



2

bp hp



2



hd ycg



hp

3















2











Jc 0.002884m

4



- iloraz modułów sprężystości stali i betonu:

n

Es

Ecm



n

6.56



- zastępcze pole powierzchni przekroju zespolonego (przekrój sprowadzony o właściwościach stali):

Az

As

Ac

n





Az 0.1065m

2



- odległość od środka ciężkości przekroju betonowego do środka ciężkości przekroju stalowego:

a

ycd ysg





a

1.0099 m



15

- odległość od środka ciężkości przekroju stalowego do środka ciężkości przekroju zespolonego:

as

Ac

n Az



a





as 0.6345m



- odległość od środka ciężkości przekroju betonowego do środka ciężkości przekroju zespolonego:

ac

As
Az

a





ac 0.3755m



- moment bezwładności przekroju zespolonego:

Jz

Js

Jc

n



As as

2





Ac

n

ac

2







Jz 0.03603394m

4



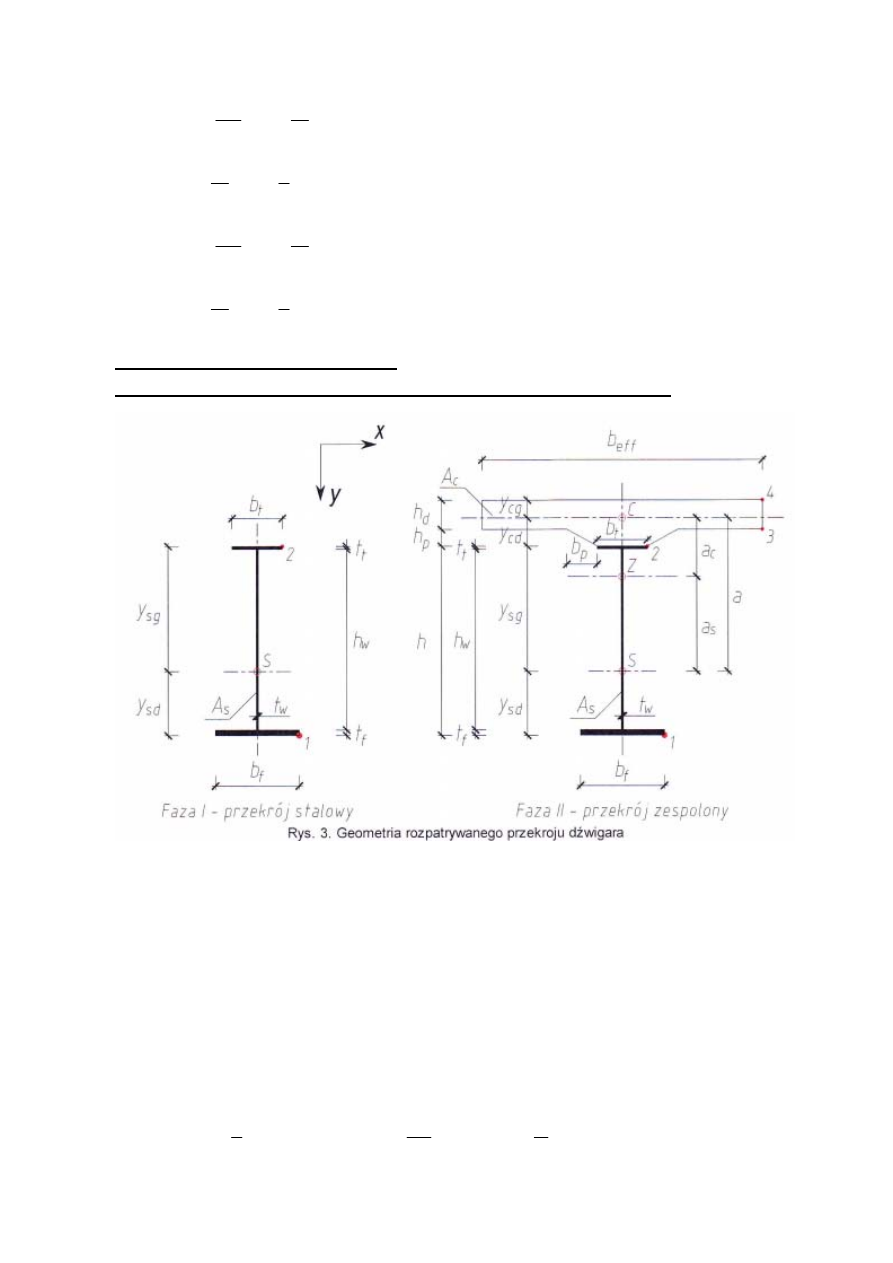
UWAGA!!!!!

Wartości naprężeń wyznaczamy w wybranych punktach przekroju, uznanych za newralgiczne -
oznaczonych na rys. 3 odpowiednio 1,2,3,4.

Wartości naprężeń - Faza I



- od obciążeń stałych:

σs1.I

Msd.I

Js

ysd





σs1.I

35.34 MPa





σs2.I

Msd.I

Js

ysg



 





σs2.I

63.55



MPa





Wartości naprężeń - Faza II



- od elementów wyposażenia:

σs1.II

Msd.II

Jz

as ysd











σs1.II

14.19 MPa





σs2.II

Msd.II

Jz

ac



ycd











σs2.II

2.29



MPa





σc2.II

Msd.II

Jz n



ac



ycd











σc2.II

0.35



MPa





σc3.II

Msd.II

Jz n



ac



hd ycg

















σc3.II

0.59



MPa





σc4.II

Msd.II

Jz n



ac



ycg











σc4.II

1.01



MPa





16

- od obciążeń ruchomych:

σr1.II

Mrd.II

Jz

as ysd











σr1.II

58.35 MPa





σr2.II

Mrd.II

Jz

ac



ycd











σr2.II

9.43



MPa





σr2.II

Mrd.II

Jz n



ac



ycd











σr2.II

1.44



MPa





σr3.II

Mrd.II

Jz n



ac



hd ycg

















σr3.II

2.42



MPa





σr4.II

Mrd.II

Jz n



ac



ycg











σr4.II

4.14



MPa





3.2. Wyznaczanie naprężeń normalnych od pełzania betonu

Zastępcze charakterystyki geometryczne przekroju zespolonego - Faza II



- mnożnik do pełzania w zależności od rodzaju obciążenia (stałe);

- średnia wilgotność względna:

- wiek betonu przy pierwszym obciążeniu mierzony w dniach:

- przekrój płyty betonowej pomostu (całej):

- obwód pola przekroju płyty betonowej stykający się z powietrzem:

- miarodajny wymiar przekroju:

ψc

1.1



RH

80%



t0

28



Acd

2.192 m

2





u

16.712 m





h0

2.Acd

u



h0 0.26m



- końcowy współczynnik pełzania (rys. 3.1 PN-EN 1992-1-1, pkt. 3.1.4 - cement N):

- zastępczy moduł sprężystości betonu uwzględniający pełzanie:

φ

1.8



Ecc

Ecm

1 ψc φ







Ecc 10.74 GPa





- iloraz modułów sprężystości uwzględniający wpływ pełzania:

nc

Es

Ecc



nc 19.56



- zastępcze pole powierzchni przekroju zespolonego (przekrój sprowadzony o właściwościach stali):

Azc

As

Ac

nc





Azc 0.0621m

2



17

- odległość od środka ciężkości przekroju stalowego do środka ciężkości przekroju zespolonego:

asc

Ac

nc Azc



a





asc 0.3654m



- odległość od środka ciężkości przekroju betonowego do środka ciężkości przekroju zespolonego:

acc

As

Azc

a





acc 0.6445m



- moment bezwładności przekroju zespolonego:

Jzc

Js

Jc

nc



As asc

2





Ac

nc

acc

2







Jzc 0.02498378m

4



Wartości naprężeń od obciążeń długotrwałych; betonowanie płyty betonowej w technologii bez



użycia rusztowań (obciążenie elementami wyposażenia) - Faza II

σs1.c

Msd.II

Jzc

asc ysd











σs1.c

15.39 MPa





σs2.c

Msd.II

Jzc

acc



ycd











σs2.c

8.38



MPa





σc2.c

Msd.II

Jzc nc



acc



ycd











σc2.c

0.43



MPa





σc3.c

Msd.II

Jzc nc



acc



hd ycg

















σc3.c

0.54



MPa





σc4.c

Msd.II

Jzc nc



acc



ycg











σc4.c

0.75



MPa





3.3. Wyznaczanie naprężeń normalnych od skurczu betonu z uwzględnieniem pełzania

Zastępcze charakterystyki geometryczne przekroju zespolonego - Faza II



- mnożnika od skurczu:
- zastępczy moduł sprężystości betonu uwzględniający skurcz:

ψs

0.55



Ecs

Ecm

1 ψs φ







Ecs 16.08 GPa





- iloraz modułów sprężystości uwzględniający wpływ skurczu:

ns

Es

Ecs



ns 13.06



- zastępcze pole powierzchni przekroju zespolonego (przekrój sprowadzony o właściwościach stali):

Azs

As

Ac

ns





Azs 0.0732m

2



- odległość od środka ciężkości przekroju stalowego do środka ciężkości przekroju zespolonego:

ass

Ac

ns Azs



a





ass 0.4638m



18

- odległość od środka ciężkości przekroju betonowego do środka ciężkości przekroju zespolonego:

acs

As

Azs

a





acs 0.5461m



- moment bezwładności przekroju zespolonego:

Jzs Js

Jc
ns



As ass

2





Ac

ns

acs

2







Jzs 0.02898907m

4



Wartość całkowitego odkształcenia skurczowego:



- współczynnik zależny od miarodajnego wymiaru h0 (wartości pośrednie należy interpolować):

kh

200

h0

mm















0.85 0.75



(

)



300 200



0.85





kh 0.788



- współczynnik:

βRH

1.55 1

RH

100%









3

















βRH

0.7564



αds1

4



- współczynniki zależne od klasy cementu (cement N):

αds2

0.12



- nominalne odkształcenie skurczu przy wysychaniu:

εcd.0

0.85 220 110 αds1









exp

αds2



fcm

10 MPa



















βRH



10

6







εcd.0

0.000269



- odkształcenie skurczowe przy wysychaniu:

εcd

kh εcd.0





εcd

0.000212



- odkształcenie końcowe skurczu autogenicznego zależne od klasy betonu:

εca

2.5

fck

MPa

10

















10

6







εca

0.000050



- odkształcenie skurczowe:

εcs

εcd εca





εcs

0.000262



Wartości sił wewnętrznych wywołanych skurczem betonu z uwzględnieniem pełzania:



- współczynnik częściowy bezpieczeństwa:

- pole powierzchni przekroju betonowego:

Wartość sił wewnętrznych:

γSH

1.00



Ac 0.439 m

2





Ns

εcs Ecs



Ac



γSH





Ns 1849.05 kN





Ms

Ns acs





Ms 1009.85 kN m







19

Wartości naprężeń od odkształceń skurczu - Faza II



σs1.s

Ns



Azs

Ms
Jzs

asc ysd













σs1.s 3.17 MPa





σs2.s

Ns



Azs

Ms
Jzs

acc



ycd













σs2.s

40.73



MPa





σc2.s

Ns
Ac

Ns



ns Azs





Ms

ns Jzs



acc



ycd













σc2.s

1.09 MPa





σc3.s

Ns
Ac

Ns



ns Azs





Ms

ns Jzs



acc



hd ycg



















σc3.s

0.77 MPa





σc4.s

Ns
Ac

Ns



ns Azs





Ms

ns Jzs



acc



ycg













σc4.s

0.21 MPa





3.4. Wpływ zmian termicznych na dźwigar zespolony

Wartości sił wewnętrznych wywołanych oddziaływaniami termicznymi - Faza II



- współczynnik rozszerzalności liniowej stali i betonu:

- różnica temperatury pomiędzy płytą żelbetową, a konstrukcją stalową:

- temperatura w środku ciężkości przekroju betonowego (płyty):

αt

10 10

6





1

C





Δ

T

10C



Δ

Tc

hd hp



ycg



hd hp



Δ

T





Δ

Tc 6.07C



- współczynnik częściowy bezpieczeństwa:

- pole powierzchni przekroju betonowego:

- współczynnik sprężystości podłużnej betonu:

- odległość od środka ciężkości przekroju betonowego do środka ciężkości
przekroju zespolonego:

Wartość sił wewnętrznych:

γQ.t

1.50



Ac 0.44m

2



Ecm 32 GPa





ac 0.38m



Nt

αt

 ΔTc



Ecm



Ac



γQ.t





Nt

1278.84



kN





Mt Nt ac





Mt

480.15



kN m







Wartości naprężeń termicznych - Faza II



σs1.t

Nt



Az

Mt

Jz

as ysd













σs1.t

2.45



MPa





σs2.t

Nt



Az

Mt

Jz

ac



ycd













σs2.t

14.34 MPa





σc2.t

Nt

Ac

Nt



n Az





Mt

n Jz



ac



ycd













σc2.t

0.73



MPa





20

σc3.t

Nt

Ac

Nt



n Az





Mt

n Jz



ac



hd ycg



















σc3.t

0.48



MPa





σc4.t

Nt

Ac

Nt



n Az





Mt

n Jz



ac



ycg













σc4.t

0.06



MPa





3.5. Zestawienie naprężeń normalnych

Elementy

wyposażenia

Obciążenie

ruchome

Pełzanie

betonu

Skurcz

betonu

min

max

1

35,34

14,19

58,35

15,39

3,17

-2,45

2,45

123,99 126,44

2

-63,55

-2,29

-9,43

-8,38

-40,73

14,34 -14,34 -110,04 -124,38

2

-

-0,35

-1,44

-0,43

1,09

-0,73

0,73

-1,86

-1,13

3

-

-0,59

-2,42

-0,54

0,77

-0,48

0,48

-3,26

-2,78

4

-

-1,01

-4,14

-0,75

0,21

-0,06

0,06

-5,75

-5,69

Punkt

Suma [MPa]

St

al

Be

to

n

Oddziaływanie

termiczne

Faza II [MPa]

Faza I

[MPa]

fyd 365.217 MPa





σs

123.99 MPa



fyd



1





fcd 21.429 MPa





σc

5.75 MPa



fcd



1





3.6. Naprężenia styczne (w przekroju podporowym)

Sprawdzenie utraty stateczności środnika nieużebrowanego przed wyczerpaniem nośności:



- parametr zależny od gatunku stali (η=1.20 <=S460, η=1.00 >S460)

- współczynnik (fyk wstawiamy w MPa)

η

1.20



ε

235

fyk

1

MPa





ε

0.75



- wysokość środnika:

- grubość środnika:

Stateczność lokalna środnika:

hw 1.2m



tw 0.011m



hw

tw

109.091



i

72

ε

η



44.881



---->

hw

tw

72

ε

η





1



Faza I



- wartość obliczeniowa sił poprzecznej:

VEd.1

Tsd.I



VEd.1 178.268 kN





- moment statyczny przekroju stalowego poniżej środka ciężkości względem własnej osi głównej:

S1

bf tf



ysd

tf

2

















tw ysd tf









ysd tf



2







S1 0.009188 m

3





- moment bezwładności przekroju stalowego:

J1

Js



J1 0.010221m

4



21

- grubość w rozpatrywanym punkcie:

t

tw



t

0.011 m



Wartość naprężeń stycznych - Faza I

τED.1

VEd.1 S1



J1 t



τED.1

14.567 MPa





Faza II



- wartość obliczeniowa sił poprzecznej:

VEd.2

Tsd.II Trd.II





VEd.2 392.698 kN





- moment statyczny przekroju stalowego poniżej środka ciężkości względem własnej osi głównej:

S2

bf tf



ysd

tf

2



as

















tw ysd tf



as









ysd tf



as



2







S2 0.026447 m

3





- moment bezwładności przekroju stalowego:

J2

Jz



J2 0.036034m

4



- grubość w rozpatrywanym punkcie:

t

tw



t

0.011 m



Wartość naprężeń stycznych - Faza I

τED.2

VEd.2 S2



J2 t



τED.2

26.201 MPa





Wartość sumaryczna naprężeń stycznych:



τED

τED.1 τED.2





τED

40.769 MPa





τED

ft



1



3.7. Naprężenia zastępcze przy jednoczesnym obciążeniu belki momentem zginającym i siłą
poprzeczną (w przekroju przęsłowym)

Faza I



- wartość naprężeń normalnych

σ1

σs1.I



σ1

35.341 MPa





- wartość naprężeń stycznych

τ1

0



τ1

0 MPa





Faza II



- wartość naprężeń normalnych

σ2

σs1.II σr1.II





σ2

72.542 MPa





- wartość obliczeniowa siły poprzecznej:

V

Qd

1
2





V

142.8 kN





- moment statyczny przekroju stalowego poniżej środka ciężkości względem własnej osi głównej:

S

S2



S

0.026447 m

3





22

- moment bezwładności przekroju zespolonego:

J

Jz



J

0.036034 m

4



- grubość w rozpatrywanym punkcie:

t

tw



t

0.011 m



Wartość naprężeń stycznych - Faza II

τ2

V S



J t





τ2

9.528 MPa





Wartość sumaryczna naprężeń normalnych



σ

σ1 σ2





σ

107.883 MPa





Wartość sumaryczna naprężeń normalnych



τ

τ1 τ2





τ

9.528 MPa





Wartość sumaryczna naprężeń normalnych



σred

σ

2

3 τ

2







σred

109.138 MPa





σred

fyk

γMO



1



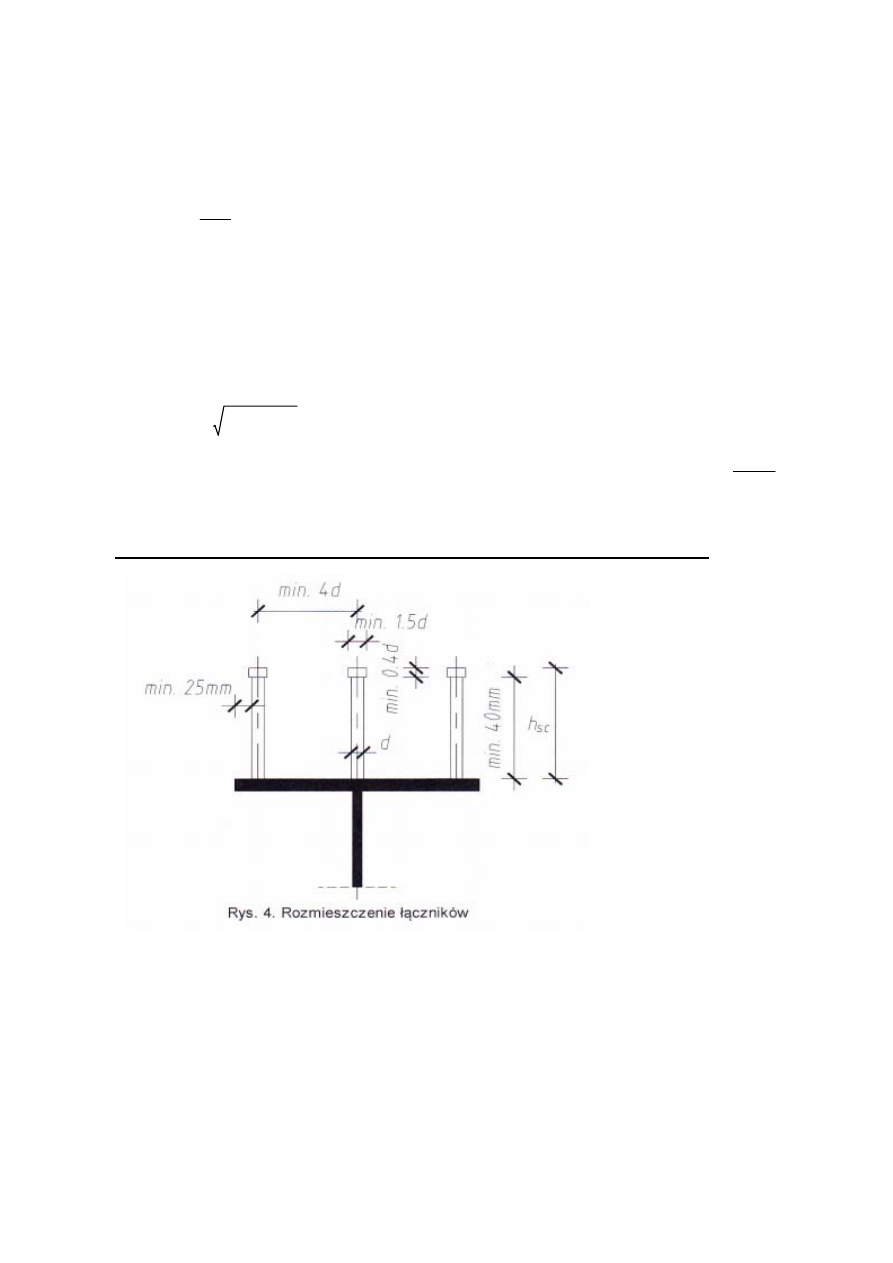
3.8. Obliczenie łączników zespalających płytę betonową z dźwigarem stalowym

- średnica łącznika (16mm < d < 25mm):

- wysokość całkowita łącznika (min. 3d):

- liczba łączników w rzędzie:

- grubość płyty:

- podłużny rozstaw łączników:

d

20 mm





hsc

200 mm





nsc

3



hd 0.21m



eI 300 mm





5 d



100 mm





5 d



eI



800mm



1



------->

23

- ilość łączników przypadająca na 1mb:

nsw

1

eI

nsc





nsw 10

1

m



Wartość siły rozwarstwiającej od obciążeń stałych i użytkowych - Faza II



- wartość obliczeniowa maksymalnej siły poprzecznej:

VII

Tsd.II Trd.II





VII 392.698 kN





- moment statyczny przekroju betonowego względem środka ciężkości przekroju zespolonego:

Sc

Ac ac





Sc 0.164878 m

3





- sprowadzony moment bezwładności przekroju zespolonego:

- iloraz modułów sprężystości stali i betonu:

Wartość jednostkowej siły rozwarstwiającej (na 1mb)

Jz 0.036034m

4



n

6.56



VL.II

VII Sc



n Jz





VL.II 273.8

kN

m





Nośność łączników:



- częściowy wspólczynnik bezpieczeństwa:

- wytrzymałość charakterystyczna na rozciąganie materiału sworznia
(fu<=500MPa):

- wytrzymałość charakterystyczna betonu na ściskanie:

- współczynnik sprężystości podłużnej betonu:

- współczynnik

γv

1.25



fu

470 MPa





fck 30 MPa





Ecm 32 GPa





α

0.2

hsc

d

1



















gdy

3

hsc

d



4



0



α

1.00



gdy

hsc

d

4



1



Obliczeniowa nośność na ścinanie łącznika:

PRd.1

0.8 fu



π

d

2


4



1

γv





PRd.1 94.499 kN





PRd.2

0.29 α

 d

2



fck Ecm





1

γv





PRd.2 90.925 kN





PRd

min PRd.1 PRd.2









PRd 90.925 kN





Sprawdzenie nośności łączników



nsw PRd



909.251

kN

m





VL.II nsw PRd





1



24

3.9. Przemieszczenia dźwigara zespolonego
3.9.1. Przemieszczenia pionowe od obciążeń ruchomych
- rozpiętość teoretyczna przęsła:

- współczynnik sprężystości podłużnej stali:

- moment bezwładności przekroju stalowego względem własnej osi ciężkości:

- moment bezwładności przekroju zespolonego:

- wartość charakterystyczna momentu zginającego w środku rozpiętości
przęsła:

- wartość ugięcia dopuszczalnego:

Lt 18m



Es 210 GPa





Js 0.010221m

4



Jz 0.036034m

4



Mrk.II 1435.85 kN m







δdop

Lt

400



δdop

45 mm





Maksymalna wartość ugięcia od obciążeń zmiennych

δr

5

48

Mrk.II Lt

2



Es Jz







δr

6.404 mm





δr

δdop



1



3.9.2. Podniesienie wykonawcze

- rozpiętość teoretyczna przęsła:

- współczynnik sprężystości podłużnej stali:

- moment bezwładności przekroju stalowego względem własnej osi
ciężkości:

- moment bezwładności przekroju zespolonego:

Lt 18m



Es 210 GPa





Js 0.010221m

4



Jz 0.036034m

4



Pionowe przemieszczenie trwałe dźwigara stalowego:



δt

1

4000

Lt





δt 4.5 mm





Pionowe przemieszczenie od obciążeń stałych w stadium montażowym



(przed zespoleniem)

- wartość charakterystyczna momentu zginającego w środku rozpiętości
przęsła

Msk.I 562.72 kN m







δs.I

5

48

Msk.I Lt

2



Es Js







δs.I

8.848 mm





Pionowe przemieszczenie od obciążeń stałych po zespoleniu



- wartość charakterystyczna momentu zginającego w środku
rozpiętości przęsła

Msk.II 328.549 kN m







δs.II

5

48

Msk.II Lt

2



Es Js







δs.II

5.166 mm





25

Pionowe przemieszczenie od skurczu betonu z uwzględnieniem pełzania



- moment bezwładności przekroju zespolonego

- wartość odkształceń skurczowych

- wartość charakterystyczna momentu zginającego

Jzs 0.028989m

4



εcs

0.000262



Ms 1009.848 kN m







δcs.II

Ms Lt

2



8 Es



Js



1

Js

Jzs



















δcs.II

12.336 mm





Pionowe przemieszczenie od obciążeń ruchomych



δr.II

0.25 δr





δr.II

1.601 mm





Strzałka podniesienia wykonawczego

δw

δt δs.I



δs.II



δcs.II



δr.II





δw

32.45 mm





Przyjęto odwrotną strzałkę ugięcia równą δw

33 mm





26