Akademia Górniczo-Hutnicza

im. S. Staszica w Krakowie

Podstawowe prawa i definicje elektrotechniki

Wykonał :

Marcin Szybowski

Elektrotechnika gr.8

Rok 2001/2002

Spis treści

Prawo Coulomba

Coulomb wykrył doświadczalnie, że dwa dostatecznie małe ciała naelektryzowane, oddalone od siebie na odległość r, z których jedno naładowane jest ładunkiem Q₁ drugie zaś ładunkiem Q₂ oddziaływają na siebie z siłą

[N]

gdzie k ma następującą postać :

Jeżeli ciała, które na siebie oddziałują, zamiast w próżni znajdują się w innym środowisku stanowiącym dielektryk, to w mianowniku wzoru Coulomba zamiast przenikalności elektrycznej próżni ε₀ należy podstawić przenikalność elektryczną danego środowiska oznaczoną przez ε. Charakteryzuje ona środowisko pod wzglę­dem jego udziału w zjawiskach elektrycznych, zachodzących w przestrzeni miedzy ciałami naładowanymi. Zazwyczaj dla celów praktycznych przyjęto porównywać przenikalność elektryczną środowiska ε z przenikalnością elektryczną próżni ε₀. Stosunek przenikalności środowiska ε do przenikalności próżni ε₀ nazywamy przenikalnością względną i oznaczamy przez ε_r czyli

Przenikalność elektryczna względna wskazuje, ile razy przenikalność elektryczna środowiska jest większa od przenikalności elektrycznej próżni. Przenikalność względna nosi również nazwę stałej dielektrycznej.

Pole elektryczne

Miedzy ciałami naładowanymi elektrycznie istnieją siły wzajemnego oddziaływania. Przestrzeń, w której istnieje stan elektryczny, prze­jawiający się w postaci wywierania sił na ładunki elektryczne znajdujące się w tej przestrzeni lub, w której przewodniki elektryzują się przez indukcję, nazywamy polem elektrycznym. Pole elektryczne dokoła ciała naelektryzowanego rozciąga się w przestrzeni nieograniczenie, jednak przy wielkich odległościach oddziaływanie jego zmniejsza, się do zera.

Jeżeli w polu naładowanego przewodnika, np. kuli metalowej, umieścimy małe lekkie ciało podłużnego kształtu zawieszone na jedwabnej nitce, np. pałeczkę to zauważymy, że pa­łeczka ustawi się w kierunku promienia kuli, wskazując na obu końcach różnoimienne ładunki elek­tryczne. Pałeczka naelektryzowała się przez indukcję i wytworzyły się dwa bieguny - dodatni i ujemny, tworząc tak zwany dipol elektryczny. Oś podłużna tak usta­wionego dipola wskazuje kierunek działania sił w polu elektrycznym. Przesuwa­jąc dipol wzdłuż jego osi w polu elektrycznym, przesuwamy się po linii, wzdłuż której działają siły pola. Linie te nazywamy liniami sił pola elektrycznego. W przypadku, gdy naelektryzowanym ciałem jest kula, linie sił pola elektrycznego pokrywają się z kierunkiem promieni wychodzących ze środka kuli. Jeżeli kula naładowana jest dodatnio (ma ładunek dodatni) to linie sił pola elektrycznego oznaczamy umownie jako skierowane na zewnątrz kuli, gdy zaś naładowana jest ujemnie (ma ładunek ujemny) to linie sił pola oznaczamy jako skierowane do kuli.

Jeżeli byśmy umieścili w pobliżu siebie dwie metalowe kule naładowane różnoimiennie, miedzy nimi zaś przesuwalibyśmy dipol w kierunku jego własnej osi, to zakreśli on linie krzywe, które będą liniami pola elektrycznego miedzy naładowanymi kulami (rys. 1.). Styczne w każdym punkcie krzywych wskazują kierunek działania sił pola elektrycznego. Pole elektryczne niezmienne w czasie nazywamy wiem elektrostatycznym.

Natężenie pola elektrycznego

Jeżeli w jakimś punkcie przestrzeni umieścimy ciało naładowane ładunkiem dodatnim +Q, to wytwarza ono wokół siebie pole elektryczne. Umieszczając teraz w dowolnym punkcie pola mały ładunek próbny +q zauważymy, że oddziaływa na niego pole ładunku +Q z siłą F proporcjonalną, wg prawa Coulomba, do ładunku +q.

Stosunek siły F do wartości ładunku +q nazywamy natężeniem pola elektrycznego w danym punkcie i oznaczymy symbolem E. Otrzymamy, zatem

W otoczeniu ciała o ładunku Q powstaje od niego pole elektryczne, którego natężenie w jakimś punkcie możemy znaleźć ze wzoru

We wzorze tym przez r oznaczono odległość punktu, w którym mierzymy natężenie pola od ładunku +Q, przez q zaś próbny ładunek elektryczny umieszczony w tym punkcie.

Natężenie pola jest wektorem, którego kierunek jest styczny do linii pola w danym punkcie i którego wartość zależy tylko od współrzędnych, wyznaczających położenie danego punktu.

Jednostką jest wolt na metr [W/m].

Jeżeli we wszystkich punktach pola natężenie jest jednakowe zarówno, co do wartości jak i kierunku, to pole takie na­zywamy polem jednorodnym. W przy­padku gdy, pole elektryczne wytworzo­ne jest przez kilka naładowanych ciał, to natężenie pola w jakimś punkcie bę­dzie wypadkową geometryczną natężeń składowych.

Napięcie

Jeżeli w punkcie A pola elektrycznego, pochodzącego np. od kuli naładowanej, umieścimy ładunek próbny +q, to na ładunek ten będzie działać siła

F=qE

gdzie E jest natężeniem pola w punkcie A.

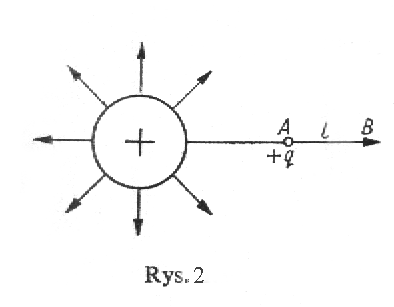
Obliczmy pracę, jaką wykonają siły pola przy przesunięciu ładunku +q na drodze l z punktu A do punktu B, gdy ładunki te jako jednoimienne odpychają się (rys. 2). Ponieważ siła F zmienia się wzdłuż drogi l, to dzieląc ją na odcinki dostatecznie małe dl takie, aby można było przyjąć na tych długościach siłę F jako stałą, znajdziemy pracę A jako

Gdyby ładunek poruszał się nie po linii natężenia pola, lecz po innej drodze, to praca A_AB może być wyrażona wzorem

gdzie cos(E, dl) jest kątem pomiędzy kierunkiem natężenia pola E oraz drogi dl.

Stosunek pracy wykonanej przez siły pola przy przesunięciu ładunku q od punktu A do B do wartości tego ładunku, czyli

zależy jedynie od położenia punktów A i B i nazywamy go napięciem miedzy punktami A oraz B i oznaczamy znakiem U_AB.

Otrzymamy zatem

Napięcie jest wielkością skalarną. Gdy przy przesunięciu ładunku l kulomba od punktu A do punktu B siły pola wykonają pracę l dżula, to napięcie miedzy punktami A oraz B jest równe woltowi (V), czyli w układzie Ze wzoru na napięcie zauważymy, że jeżeli napięcie punktu A względem B wynosi V_AB, to praca wykonana przez siły pola przy przesunięciu ładunku +q wyniesie W_AB = qU_AB.

Potencjał

Napięcie w jakimś punkcie A pola elektrycznego względem innego punktu, w którym napięcie przyjęto równe zeru, nazywamy potencjałem w punkcie A. Ponieważ w punkcie nieskończenie odległym od punktu A, w którym umieszczony jest ładunek +Q, wytwarzający pole elektryczne, siła działająca na jakikolwiek ładunek jest równa zeru, co wynika z prawa Coulomba, to przy przesuwaniu ładunku jednostkowego z punktu A do nieskończoności, gdzie siły pola mają wartość równą zeru, zostanie wykonana praca, która równa się liczbowo poten­cjałowi pola w punkcie A. Zatem potencjał w jakimś punkcie pola będzie się równał liczbowo pracy wyko­nanej przez siły pola przy przesunięciu jednostkowego ładunku elektrycznego z danego punktu do nieskończoności. Ponieważ pomiar tak zdefiniowanej pracy wykonanej przez siły pola jest niemożliwy, wiec ze względów praktycznych przy­jęto uważać potencjał ziemi za równy zeru i względem niej mierzyć pracę wyko­naną przy przesuwaniu ładunku; jednak we wzorach teoretycznych dla ścisłości obliczeń uwzględnia się przesunięcie ładunku do nieskończoności. Potencjał w punkcie A oznaczamy umownie symbolem V_A, W myśl, zatem powyższej definicji potencjału możemy napisać

Powierzchnie ekwipotencjalne

W otoczeniu naelektryzowanego ciała o potencjale V wszystkie punkty prze­strzeni mają różne potencjały. Istnieją jednak takie zbiory punktów, których potencjał jest jednakowy. Wszystkie te punkty leżą w ogólności na pewnych krzywych powierzchniach, otaczających naelektryzowane ciało. Powierzchnie takie nazywamy powierzchniami jednakowego potencjału, czyli ekwipotencjalnymi. Wo­kół ciała naelektryzowanego można wyrysować dowolną liczbę linii lub po­wierzchni ekwipotencjalnych, przy czym na każdej powierzchni potencjał będzie miał inną wartość. Ponieważ między dwoma jakimikolwiek sąsiednimi punktami krzywej ekwipotencjalnej nie ma różnicy potencjałów, to składowa styczna natężenia pola w każdym punkcie krzywej będzie równa zeru i pozostanie tylko skła­dowa normalna. Gdyby istniała składowa styczna E to, ponieważ natężenie pola jest skierowane od potencjału większego do mniejszego, na powierzchni ekwipo­tencjalnej istniałby spadek potencjału, co w myśl definicji o powierzchniach ekwipotencjalnych jest niemożliwe. Powierzchnią ekwipotencjalną jest np. po­wierzchnia każdego przewodnika pod warunkiem, aby przez niego nie przepływał żaden prąd, gdyż wtedy istniałby na nim spadek napięcia.

Indukcja elektryczna (przesuniecie elektryczne)

Po zbliżeniu ciała naelektryzowanego do nienaelektryzowanego indukują się na nim ładunki elektryczne. Jeżeli w polu elektrycznym naładowanej kuli umieścimy np. płytkę próbną, to ładunki na niej pod wpływem pola zostają przesunięte w ten sposób, że na stronie zwróconej do kuli grupują się ładunki przeciwnego znaku niż ładunek kuli, na stronie zaś przeciwnej ładunki zgodne.

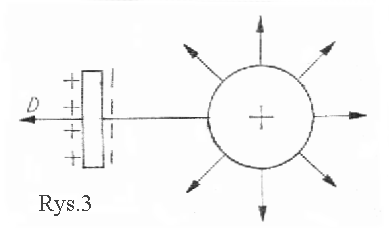
Z tego powodu indukcję elektryczną nazy­wamy również przesunięciem elektrycznym i oznaczamy przez D.

Indukcja elektryczna, jako przesunięcie elektronów w płytce, jest wielkością wektorową, której kierunek jest zgodny z kierunkiem linii pola w danym punkcie. Miarą indukcji jest stosunek ładunku indukowanego q na powierzchni płytki, umieszczonej w jakimś punkcie pola prostopadle do linii pola, do wielkości jed­nostronnej powierzchni tej płytki. Możemy za­tem wyrazić indukcję elektryczną D jako

gdzie q jest indukowanym ładunkiem płytki, S — jednostronnym polem powierzchni płytki. Jeżeli ładunek indukowany wyrazimy w kulombach (C), powierzchnię S w m², to jednostkę indukcji otrzymamy w C/m².

Jeżeli pole nie jest jednorodne, to indukcja jest większa w tych miejscach, w których natężenie pola jest większe.

Związek między natężeniem pola elektrycznego i indukcją elektryczną wyraża się wzorem:

z wzoru tego można znaleźć względna przenikalność elektryczna ośrodka jako

gdzie ε₀ jest przenikalnością elektryczną próżni, natężenie zaś poła, jak i indukcję, można pomierzyć za pomocą metod znanych w fizyce.

Pojemność

Jeżeli dwie jednakowe płytki zbliżone do siebie, lecz rozdzielone dielektry­kiem, np. powietrzem, naładowaliśmy ładunkiem +Q oraz -Q, to wytworzy się między nimi napięcie. Układ taki nazywamy kondensatorem, zaś tworzące go płytki - okładzinami kondensatora. Stosunek ładunku znajdującego się na okła­dzinach kondensatora do napięcia między nimi nazywamy pojemnością konden­satora i oznaczamy przez C. Możemy, zatem napisać:

Widzimy, więc, że liczbowo ładunek przypadający na l wolt jest dla danego kondensatora stały. Pojemność kondensatora zależy od jego wymiarów, kształtu i rodzaju dielektryka między okładzinami. W układzie SI jednostką pojem­ności jest farad (F). Kondensator ma pojemność l farada, gdy po wprowadzeniu nań ładunku l kulomba uzyska potencjał l wolta. Ponieważ farad jest jednostką zbyt dużą, to dla celów praktycznych używa się jednostek mniejszych, mianowicie mikrofaradów: l µF = 10^-6 F oraz pikofaradów l pF = 10^-12 F.

Zazwyczaj zamiast powietrza jako die­lektryka używa się innych materiałów izo­lujących płytki od siebie. Jako materiału na okładziny w kondensatorach używa się zwykle folii cynowej lub aluminiowej, jako dielektryk zaś stosuje się mikę, papier nasycony lakierem izolacyjnym, a czasem szkło.

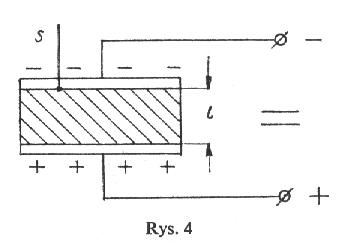
Najprostszym kondensatorem jest kondensator piaski (rys.4), składający się z dwóch płytek, oddzielonych dielektrykiem. Gdy do takiego kondensatora doprowadzić napięcie, na okładzinach jego pojawi się ładunek elektryczny - dodatni na okładzinie przyłączonej do bieguna dodatniego, ujemny zaś na okładzinie przyłączonej do bieguna ujemnego. Jeżeli teraz okładziny naładowanego kondensatora połączymy przewodnikiem, to przepłyną po nim ładunki elektryczne.

Prąd ładunków elektrycznych płynie pod wpływem działania tzw. siły elektromotorycznej pojemności równej

która w miarę ubywania ładunku maleje.

Strumień (elektryczny i magnetyczny)

Strumień (symbol Φ ) jest własnością wszystkich pól wektorowych. Jest to wielkość skalarna.

Aby zrozumieć jego znaczenie wygodnie jest się posłużyć strumieniem przepływu cieczy Φ_v np. wody. Jeżeli teraz przez S oznaczymy powierzchnie, przez którą przepływa nasza ciecz, a przez A ilość tej ciecz to możemy zapisać.

Teraz postępując analogicznie, ale zastępując A wektorem pola elektrycznego E możemy zapisać równanie na strumień elektryczny

lub w postaci całkowej

Różnica w stosunku do cieczy polega na tym, że tutaj nie występu żaden przepływ.

Zastępując wektor pola elektrycznego E wektorem pola magnetycznego H otrzymamy wzór na strumień magnetyczny

Jednostką strumienia elektrycznego jest [V*m], strumienia magnetycznego Weber [Wb].

Prawo Gaussa

Strumień elektryczny przez powierzchnię zamkniętą równa się ładunkowi zawartemu we wnętrzu tej powierzchni i podzielonemu przez przenikalność elektryczną ε.

Co możemy zapisać w postaci:

Oznacza to, że pole elektryczne jest polem źródłowym, a źródłem pola elektrycznego jest ładunek. Źródłem linii pola elektrycznego są ładunki, przy czym linie pola zaczynają się na ładunkach dodatnich, a kończą na ładunkach ujemnych. Linie pola elektrycznego maja zatem początek oraz koniec i nie są liniami zamkniętymi.

Prawo Gaussa dla magnetyzmu

Strumień magnetyczny przez powierzchnię zamkniętą równa się zero.

Oznacza to, że nie istnieje w przyrodzie ładunek magnetyczny. Linie indukcji pola magnetycznego są krzywymi zamkniętymi.

Obwód elektryczny

Prąd elektryczny jest przepływem elektronów swobodnych lub jonów. W prze­wodnikach, w których znajduje się dostateczna liczba elektronów swobodnych, następuje pod wpływem pola elektrycznego, wytworzonego przez różnicę poten­cjałów na końcach przewodnika, uporządkowany ruch elektronów, tworząc prąd elektryczny. W roztworach kwasów, zasad i soli następuje dysocjacja czą­steczek w roztworze i prąd elektrycz­ny tworzą przepływające przez roz­twór jony. Zamkniętą drogę, po której przesuwają się elektrony, nazywa­my obwodem elektrycznym. Prąd elek­tryczny może płynąć w obwodzie tyl­ko w przypadku, gdy istnieje w ob­wodzie źródło energii elektrycznej, po­ wodujące powstanie tzw. siły elektro­motorycznej (SEM), która zdolna jest przesunąć elektrony wzdłuż zamkniętego obwodu. Siła elektromotoryczna jest, zatem przyczyną ruchu elektronów wzdłuż obwodu. Źródło siły elektromotorycznej, zwanej często źródłem prądu, nazywa się generatorem. Najprostszy obwód elektryczny przedstawiony jest na rys.5

Obwód tworzy źródło siły elektromotorycznej (SEM) w postaci generatora G, odbiornik O i przewody łączące źródło z odbiornikiem. Za umowny dodatni zwrot prądu przyjęto zwrot, jaki miałyby ładunki dodatnie, gdyby miały możność poruszania się w przewodniku. Jest to pogląd zwyczajowo-historyczny. Zatem w przewodnikach, w których prąd elektryczny powstaje na skutek przesuwania się elektronów swobodnych mających ładunek ujemny, umowny zwrot prądu jest przeciwny do zwrotu poruszających się elektronów. Na rys.5 zwrot prądu przedstawiony jest w postaci strzałek. Zaciski generatora również oznaczono umownie znakiem plus (+) i znakiem minus (-), aby prąd w obwodzie poza generatorem przepływał od zacisku dodatniego do ujemnego. W elektrolitach i gazach zwrot poruszających się jonów dodatnich jest zgodny z umownym zwrotem prądu elektrycznego, zwrot zaś poruszających się jonów ujemnych jest przeciwny.

Natężenie prądu elektrycznego

Ponieważ ładunek jednego elektronu jest zbyt mały, wiec jako jednostkę praktyczną ilości elektryczności w układzie SI przyjęto l kulomb, którego ładunek, jak podano poprzednio, równa się 6,25*10¹⁸ elementarnych ładunków elektronu.

Stosunek ładunku elektrycznego przepływającego przez przewodnik do czasu jego przepływu nazywamy natężeniem prądu elektrycznego.

Gdy przez przewodnik przepływa ładunek l kulomba (l C) w ciągu l sekundy (l s), to mówimy, że natężenie prądu wynosi 1 amper (l A). Amper jest jed­nostką prądu w układzie SI. Natężenie prądu wynosi l amper, jeśli prąd o stałym natężeniu, przepływając w każdym z dwóch nieskończenie długich rów­noległych przewodów o pomijalnie małym przekroju, znajdujących się w próżni i odległych od siebie o l metr, wywołuje miedzy tymi przewodami siłę wzajem­nego oddziaływania równą 2*10^-7 niutonów na każdy metr długości przewodu.

Jeżeli prąd płynie nierównomiernie w czasie, to możemy mówić tylko o war­tości chwilowej natężenia prądu, którą oznaczamy literą i. Wartość chwilową natężenia prądu znajdujemy jako

przy czym dq jest elementarną ilością ładunku elektrycznego, jaka przepływa przez przewodnik w czasie dt.

Jeżeli natężenie prądu nie zmienia się w czasie, co do wartości, a wiec przy

i = I =const

ładunek elektryczny Q, jaki przepływa w czasie t, wynosi :

Q = It

Przez I oznaczamy natężenie prądu o jednakowym zwrocie i stałej wartości w rozpatrywanym okresie czasu. Prąd taki nazywamy prądem stałym

Opór i przewodność elektryczna

Podczas przepływu prądu przez przewodnik, na skutek zderzeń elektronów swobodnych przy ich ruchu międzycząsteczkowym z cząsteczkami materiału przewodnika, następuje częściowa strata energii i zamiana jej na ciepło. Wartość straconej energii zależna jest od własności przewodzącego materiału, czyli tak zwanego oporu przewodnika.

Opór zależy od rodzaju materiału, długości, przekroju i temperatury prze­wodnika. Jednostką oporu jest om i oznacza się symbolem Ω.

Jeden om jest to opór takiego przewodnika, w którym przy różnicy potencjałów miedzy jego końcami l wolta płynie prąd o natężeniu l ampera.

Opór przewodnika o długości l metra i przekroju l mm² nazywa się oporem właściwym materiału i oznacza się literą ρ. Wymiar jego jest

Ponieważ opór właściwy ρ jest oporem l metra przewodu o przekroju l mm², zatem opór przewodnika o długości l metrów i przekroju S mm², który ozna­czamy literą R, będzie l/S razy większy, czyli

Wraz ze wzrostem temperatury opór czystych metali rośnie. Objaśnia się to tym, że ze wzrostem temperatury wzrasta ruch drgający cząsteczek, utrudniający przepływ elektronów swobodnych i dlatego następuje większa strata energii przy ich przepływie.

Odwrotnością oporu jest przewodność, którą oznacza się symbolem G oraz mierzy się w simensach (S). Zatem

Jeden simens jest to przewodność przewodnika o oporze l Ω.

Odwrotność oporu właściwego nazywamy przewodnością właściwą

i mierzymy w

Siła elektromotoryczna i prawo Ohma

W czasie pracy generatora w obwodzie zamkniętym z rys.5 płynie prąd elektryczny. Przy przepły­wie prądu przez obwód zostaje zużyta energia elektryczna, która zamienia się na pracę mechaniczną, ciepło lub światło. Energię tę dostarcza przepływającym elek­tronom generator elektryczny, który w czasie pracy podnosi ich potencjał.

Przyczyna powodująca w obwodzie otwartym wytworzenie różnicy potencja­łów miedzy dwoma punktami obwodu, a w obwodzie zamkniętym przepływ prądu elektrycznego nazywa się siłą elektromotoryczną i oznacza się symbolem E oraz nazwą SEM.

Siłę elektromotoryczną, tak jak potencjał, mierzy się w woltach. Jednostką siły elektromotorycznej jest l wolt. Jeden wolt możemy również określić jako różnicę potencjałów miedzy dwoma punktami przewodnika o oporze l Ω, jeżeli płynie przez niego prąd l amper.

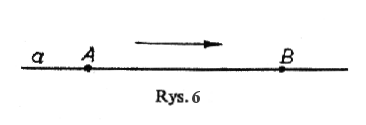
Jeżeli wzdłuż przewodu a między, punktami A i B płynie prąd elektryczny od A do B, to w punkcie A potencjał będzie wyższy niż w punkcie B (rys.6). Różnica potencjałów punktów A i B będzie napięciem lub też spadkiem napięcia między punktami A i B.

Jeżeli potencjał w punkcie A oznaczymy przez v_A, potencjał w punkcie B przez V_B, różnicę zaś potencjałów między A i B przez V_AB, to możemy napisać

U_AB =V_A - V_B

Doświadczenie wykazano, że spadek napięcia na odcinku AB jest proporcjo­nalny do natężenia prądu i przepływającego przez ten odcinek oraz do oporu odcinka R_AB, a zatem

U_AB = R_ABI

Powyższa zależność miedzy napięciem, natężeniem prądu i oporem jest wy­razem prawa Ohma.

Pierwsze Prawo Kirchoffa

W każdym węzłowym punkcie sieci algebraiczna suma prądów równa się zero, czyli ile prądu wpływa, tyle musi odpłynąć, co możemy zapisać

Drugie Prawo Kirchoffa

W każdym zamkniętym obwodzie suma algebraiczna sił elektromotorycznych równa się sumie algebraicznej spadków napięć na wszystkich elementach obwodu.

Lub inaczej w każdym zamkniętym obwodzie suma algebraiczna napięć jest równa zero. Co możemy zapisać

Moc i praca elektryczna

Wyznaczymy pracę, jaką wykonuje prąd elektryczny przepływając przez jakiś odcinek obwodu, np. od punktu A o potencjale wyższym V_A do punktu B o potencjale niższym V_B. Ponieważ potencjały w punktach A i B mierzy się pracą, jaką należy wykonać, aby przenieść elementarny ładunek z punktu A lub B do ziemi, to praca wykonana przy przesunięciu ładunku dq od punktu A do punktu B wzdłuż przewodu będzie się równać iloczynowi różnicy potencjałów w obu punktach przez przesuwany ładunek dq, czyli

przy czym
jest napięciem miedzy punktami A i B. Jeżeli przyj­miemy, że dq jest ładunkiem elektrycznym, jaki przepłynął w czasie dt, czyli

gdzie i jest wartością chwilową prądu w rozpatrywanym odcinku, to podstawia­jąc wartość na dq do wzoru poprzedniego i całkując go, otrzymamy

W przypadku stałego napięcia i przy założeniu, że natężenie prądu I jest stałe co do wartości, to otrzymamy wzór na pracę elektryczną

Wiadomo z mechaniki, że mocą układu nazywamy stosunek pracy wykonywanej przez układ do czasu jej wykonania, czyli

Przy stałych wartościach napięcia U oraz prądu I otrzymamy

Zatem moc elektryczna równa się iloczynowi napięcia i prądu przepływającego.

Jednostką mocy jest wat i oznacza się symbolem W.

Jeden wat jest to stosunek pracy elektrycznej do czasu jej trwania, wykonanej przy przepływie przez obwód prądu l ampera przy różnicy potencjałów na koń­cach obwodu równej l woltowi czyli l wat = l wolt *1 amper.

Jeżeli w wyrażeniu na pracę elektryczną moc wyrazimy w watach, a czas w sekundach, to pracę otrzymamy w watosekundach, czyli dżulach, i oznaczymy przez J.

Jak wiemy, l dżul jest to praca, jaką siła l niutona wykonuje na drodze l metra, czyli

l dżul = l N* l m.

Jeżeli we wzorze na pracę czas wyrażony jest w godzinach, to otrzymamy pracę w watogodzinach

l watogodzina = 3600 watosekund = 3,6-10^S J, 1000 watogodzin = l kilowatogodzina = l kWh = 3,6-10⁶ J.

Pole magnetyczne

Przestrzeń otaczającą magnes albo przewodnik z prądem nazywamy polem magnetycznym, podobnie jak przestrzeń w pobliżu naładowanego pręta nazywaliśmy polem elektrycznym.

Pole magnetyczne jest wektorem, którego oznaczamy jako H. Jednostką jest amper na metr [A/m] .

Indukcja magnetyczna

Niektóre ciała umieszczone w polu magnetycznym magnesują się, wytwarzając własne pole magnetyczne. Zjawisko powstawania pola własnego pod wpływem magnetycznego pola zewnętrznego nazywa się namagnesowywaniem się ciała.

Wytworzenie pola własnego przez ciała namagnesowane związane jest ze zo­rientowaniem elementarnych magnesów w ciele w kierunku wektora H pola zewnętrznego.

Krążące wokół jądra w atomie elektrony stanowią pewien rodzaj obwodu prądu elektrycznego, który wytwarza pole magnetyczne w kierunku prostopadłym do płaszczyzny orbity krążącego elektronu. Jednocześnie elektrony, wirując wokół własnej osi, stanowią także elementarne prądy, które wytwarzają dodatkowe pola magnetyczne. Atomy lub cząsteczki, w których wypadkowe pole magnetyczne wirujących elektronów nie jest równe zeru, zachowują się jak elementarne mag­nesy. Jeśli osie elementarnych magnesów w ciele skierowane są chaotycznie tak, że ich pola magnetyczne wzajemnie się znoszą, to ciało nie może wytworzyć na zewnątrz własnego pola magnetycznego. Dopiero pod wpływem pola zewnętrz­nego elementarne magnesy ustawiają się swymi osiami w kierunku wektora H, wywołując powstanie biegunów magnetycznych w ciele.

Poprzednio rozpatrywaliśmy pole magnetyczne prądów, nie biorąc pod uwagę właściwości magnetycznych środowiska, w którym znajduje się przewodnik z prądem. Prawa poprzednio wyprowadzone odnoszą się nie tylko do próżni, ale również do środowisk o zbliżonych właściwościach magnetycznych, np. powietrza.

Niektóre ciała, jak np. żelazo, nikiel i kobalt, wykazują wybitne właściwości magnetyczne i udział tych ciał w wytworzeniu wypadkowego pola magnetycznego ma zasadnicze znaczenie. W ten sposób pole wypadkowe składa się z dwóch pól, jednego zewnętrznego pochodzącego od prądu oraz drugiego pochodzącego od ciała namagnesowanego.

Jeżeli oznaczymy tak jak poprzednio, natężenie pola magnetycznego przez H, zaś natężenie pola wypadkowego przez B, to możemy napisać

Natężenie wypadkowe B nosi nazwę indukcji magnetycznej. Stosunek indukcji magnetycznej B do natężenia pola H oznaczamy symbolem µ i nazywamy bez­względną przenikalnością magnetyczną środowiska:

Bezwzględna przenikalność magnetyczna µ charakteryzuje udział środowiska w wartości wytworzonego pola magnetycznego i pokazuje, ile razy indukcja mag­netyczna B większa jest od natężenia magnetycznego przenikalność. Bezwzględną przenikal­ność magnetyczną środowiska przedstawiamy również w postaci

gdzie wielkość bezwymiarowa µ_r wskazuje, ile razy bezwzględna przenikalność magnetyczna danego środowiska jest większa od bezwzględnej przenikalności magnetycznej próżni, zaś µ₀ jest bezwzględną przenikalnością próżni. W układzie SI wartość liczbowa µ₀ ze względów przeliczeniowych wynosi

przy czym Vs (woltosekunde) nazwano weberem i oznaczono [Wb].

Jednostką indukcji magnetycznej w układzie SI jest weber na metr kwadratowy (1Wb/m²)

Przy czym 1Wb/m² = 1 tesla [T].

Prawo Ampere'a

Prawo to dotyczy wytwarzania pola magnetycznego przez przewodnik z prądem lub poruszający się ładunek. Biorąc pod uwagę, że zmienne pole magnetyczne wytwarza pole elektryczne (prąd) możemy napisać

prąd ↔ pole (B) ↔ prąd

Przykład poniżej obrazuje prawo Ampere'a.

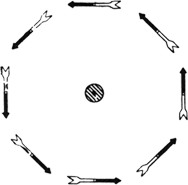
Na rys.7 przedstawiony jest drut otoczony pewną liczbą małych magnesików. Jeżeli przez drut nie płynie prąd, magnesiki układają się wzdłuż poziomej składowej ziemskiego pola magnetycznego. Kiedy przez drut płynie silny prąd, magnesiki otaczają wokoło drut wskazując, że linie pola magnetycznego wytworzonego przez ten prąd są kołami zamkniętymi.

Ilościowa zależność pomiędzy prądem i a polem magnetycznym B jest następująca

Zależność ta nosi nazwę prawa Ampere'a. Prawo Ampere'a, łącznie z jego uogólnieniem i rozszerzeniem dokonanym przez Maxwella, jest jednym z podstawowych równań teorii elektromagnetyzmu.

Prawo Biota - Savarta

Prawo Ampere'a możemy stosować do znajdowania pola magnetycznego tylko wtedy, gdy rozkład prądów jest na tyle symetryczny, że pozwala na łatwe obliczenie całki krzywoliniowej
Ogranicza to użyteczność tego prawa przy rozwiązywaniu praktycznych zagadnień. Oczywiście, prawo nie przestaje być słuszne, tylko trudno jest je zastosować. Podobnie prawo Gaussa można w elektrostatyce stosować do znajdowania pól elektrostatycznych tylko wtedy, jeśli rozkład ładunku ma na tyle wysoką symetrię, że łatwo jest obliczyć całkę powierzchniową
. Na przykład możemy użyć prawa Gaussa do znalezienia pola elektrycznego wytworzonego przez równomiernie naładowany pręt, nie możemy go jednak zastosować w przypadku dipola elektrycznego, gdyż w tym przypadku symetria rozkładu ładunku jest niewystarczająca.

W celu obliczenia natężenia E pola wytworzonego w danym punkcie przez dowolnie rozłożony ładunek, dzieliliśmy ten ładunek na elementy ładunku dq i stosując prawo Coulomba obliczaliśmy wkład dE, jaki wnosi w natężenie pola w rozważanym punkcie każdy z tych elementów. Całkowite natężenie pola E otrzymywaliśmy sumując, a właściwie całkując wkłady dE po całym ładunku.

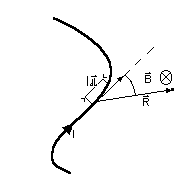
Podobnie postępujemy chcąc obliczyć w jakimś punkcie indukcję B pola magnetycznego, wytworzonego przez dowolny rozkład prądów. Dzielimy mianowicie każdy z prądów I ni nieskończenie małe elementy i stosując prawo Biota - Savarta (które podaje niżej). Obliczamy wkłady dB, dawane w rozważanym punkcie przez każdy z tych elementów. Wypadkowy wektor B w tym punkcie uzyskujemy całkując te wkłady po całym rozkładzie prądów.

Element prądu dl wytwarza w punkcie P pole magnetyczne o indukcji dB, której wartość liczbowa wynosi:

A w postaci wektorowej:

Wypadkową indukcję magnetyczną B w punkcie P znajdujemy sumując przyczynki od poszczególnych odcinków dl:

Prawo indukcji Faradaya

Prawo indukcji Faradaya głosi, że indukowana w obwodzie SEM (siła elektromotoryczna) równa jest (wyłączając znak minus) szybkości, z jaką zmienia się strumień przechodzący przez ten obwód. Jeśli szybkość zmian strumienia jest mierzona w [Wb/s], to SEM otrzymamy w woltach. Prawo to możemy przedstawić w postaci równania

Równanie to nosi nazwę prawa indukcji Faradaya. Znak minus dotyczy kierunku induko­wanej SEM

Reguła Lenza

Prąd indukowany ma taki kierunek, że przeciwstawia się zmianie, która go wywalała. Znak minus w prawie Faradaya wyraża właśnie to przeciwstawienie się.

Reguła Lenza dotyczy prądów indukowanych, co oznacza, że odnosi się ona tylko do przewodzących obwodów zamkniętych. Jeśli obwód jest otwarty, to kierunek indukowanej SEM możemy znaleźć rozważając, co by się stało, gdyby obwód ten był zamknięty.

Literatura :

1. Zygmunt Rybicki „Elektrotechnika Ogólna”.

2. Dawid Halloday, Robert Resnick „Fizyka 2”.

3. B.M. Jaworski “Fizyka - Poradnik Encyklopedyczny”.

4. Mieczysław Jerzewski „Fizyka”.

1

---