KATEDRA TECHNIKI CIEPLNEJ

Laboratorium Wymiany Ciepła

POMIAR RADIACYJNEGO STRUMIENIA CIEPŁA.

1 Wstęp

Każda powierzchnia o temperaturze powyżej 0 [ K ] otoczona płynem optycznie

przezroczystym wypromieniowuje do otoczenia strumień ciepła będący funkcją jej

temperatury T

w

4

.

Proces ten jest niezależny od zjawisk konwekcyjnych zachodzących na tej samej powierzchni.

Oznacza to, że strumień ciepła przejmowany z powierzchni jest sumą konwekcji i

promieniowania czyli:

Q = Q

k

+ Q

r

Konwekcje opisuje równanie

Q

k

= 

k

(T

w

– T

f

) A

gdzie: 

k

– wspólczynnik przejmowania ciepła wyznaczony z równań kryterialnych

T

w

– temperatura powierzchni

T

f

– temperatura płynu

A – powierzchnia

Radiacyjny strumień ciepła określa równanie

Q

r

= 

1-2

A C

o

[(T

w

/100)

4

– (T

∞

/100)

4

]

gdzie: 

1-2

= 1 / [ 1/

1

+ A/A

∞

(1/

2

– 1)] – efektywny współczynnik emisji układu

powierzchni A otoczonej powierzchnią A

∞







1

– współczynnik emisji powierzchni A



2

– wspólczynnik emisji powierzchni A

∞

otaczającej powierzchnie A

C = 5.76 [W/m

2

K

4

] – stała promieniowania

W oparciu o te równania można wyznaczyć zastępczy radiacyjny współczynnik

przejmowania ciepła



r

= Q

r

/ [(T

w

– T

f

) A]

W rezultacie łączny strumień ciepła przekazywany do otoczenia można wyznaczyć z

równania

Q = ( 

k

+ 

r

) ( T

w

– T

f

) A

zakładają, że T

∞

= T

f

2. Pomiar radiacyjnego strumienia ciepła.

Układ pomiarowy składa się z dwóch kul o średnicy D = 50 mm różniących się

emisyjnością powierzchni. Powierzchnia jednej kuli pokryta jest polerowanym chromem



1

= 0.1 a druga czarnym matowym lakierem o emisyjnosci 

1

= 0.96.

Kula wykonana jest z miedzi co zapewnia izotermiczność jej powierzchni przy

umiarkowanych intensywnościach konwekcji. Kulki grzane są prądem elektrycznym z

zasilaczy prądu stałego z jednoczesnym pomiarem prądu I i napięcia U.

Wartości wielkości mierzonych rejestruje cyfrowy system akwizycji danych pomiarowych.

Pomiar wykonyjemy w warunkach stanu ustalonego utrzymując równe temperatury obu

powierzchni. W tych warunkach konwkcyjny strumień ciepła na obu kulach będzie taki sam.

Stąd różnica mocy elektrycznej zasilającej obie kulki jest efektem większej radiacji z czarnej

kulki tzn.

Q = Q

0.96

–Q

0.1

= [Q

k

+ Q

r

]

0.96

– [Q

k

+ Q

r

]

0.1

= [Q

r

]

0.96

– [Q

r

]

0.1

Po podstawieniu relacji na radiacyjny strumień ciepła mamy

Q = [

1-2

]

0.96

A C

o

[(T

w

/100)

4

– (T

f

/100)

4

] – [

1-2

]

0.1

A C

o

[(T

w

/100)

4

– (T

f

/100)

4

]

stąd

Q =

{

[

1-2

]

0.96

– [

1-2

]

0.1

}

A C

o

[(T

w

/100)

4

– (T

f

/100)

4

]

Zakładając, że iloraz A/A

∞

≈ 0 mamy

Q = [

0.96

– 

0.1

] A C

o

[(T

w

/100)

4

– (T

f

/100)

4

]

Przyjmując tablicowe wartości dla polerowanego chromu 

0.1

= 0.1 i dla czarnego matowego

lakieru 

0.96

= 0.96 mamy wartość obliczeniową

Q = [0.96 – 0.1] A C

o

[(T

w

/100)

4

– (T

f

/100)

4

]

Mierzą tą wartość jako różnicę mocy zasilania obu kulek możemy wyznaczyć niedokładność

procedury obliczeniowej

Q

oblicz

– Q

pomiar

 = --------------------------------- 100 %
Q

pomiar

Podstawowym źródłem powyższej niedokładności jest przybliżony charakter wartości

współczynników emisyjności e odczytywanych z tablic.

Korzystając z wyników pomiarów i obliczeń wyznaczyć zmianę udziału radiacji Q

r

w

całkowitym strumieniu ciepła Q ze wzrostem temperatury powierzchni.

Q

r

R

r

=

[

------

]

T

100 %

Q

.

T

Q

r

/Q

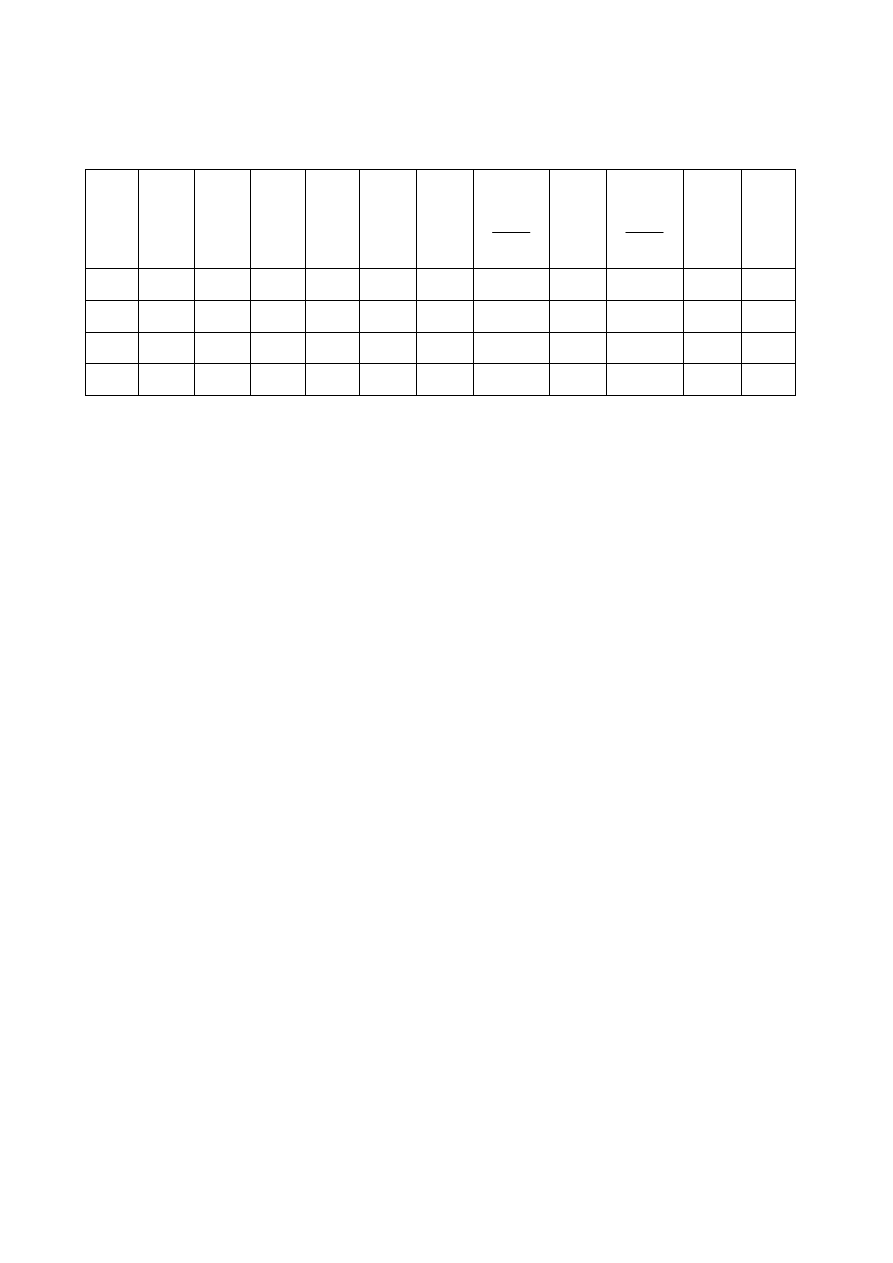
Tabela obliczeniowa 1.

lp

T

f

[K]

T

w

[K]

U

[V]

I

[A]

el

Q

[W]

r

Q

[W]

r



2

W

m K













k

Q

[W]

k



2

W

m K













Q



[W]

R

r

[%]