
Jagiellonian University
Theoretical
Computer Science
Matematyka Dyskretna
Wykład 04
WSZIB NLU
Edward Szczypka
szczypka@tcs.uj.edu.pl
zima 2013
Edward Szczypka
1 / 1

Jagiellonian University
Theoretical
Computer Science
spis
Edward Szczypka
2 / 1

Jagiellonian University
Theoretical
Computer Science
Zło˙zono ´s ´c Obliczeniowa Algorytmu
bardzo nieformalnie
jak du˙zo czasu dany algorytm potrzebuje, by wykona´c
obliczenia, w proporcji do danych wej´sciowych
nieformalnie
ile elementarnych kroków (np. dodawa ´n, mno˙ze ´n, podstawie ´n)
dany algorytm wykona przy danych wej´sciowych
pewnego rozmiaru
formalnie funkcja
t : N −→ N podaj ˛
aca liczb ˛e kroków t(n) dla
danych wej´sciowych o rozmiarze n.
Uwagi:
zamiast mierzy´c czas np. w sekundach, zliczamy kroki algorytmu.
Chodzi o to, by uniezale˙zni´c si ˛e od szybko´sci konkretnego komputera i zajmowa´c si ˛e
samym algorytmem
zwykle jako kroki wybieramy operacje wykonywana w algorytmie najcz ˛e´sciej
rozmiar danych wej´sciowych mo˙zna mierzy´c np. w bajtach, ale mo˙zna posługiwa´c si ˛e
dowolna jednostka. Zmiana jednostki oznacza jedynie przemno˙zenie rozmiaru danych
przez stała (np. 1 KB = 1024 B)
Edward Szczypka
3 / 1

Jagiellonian University
Theoretical
Computer Science
Zło˙zono ´s ´c Obliczeniowa Algorytmu - przykład
Przykład 1 Algorytm dodawania liczb z tablicy n-elementowej. Dane wej´sciowe:
T [1], T [2], . . . , T [n]
Algorytm:
i := 1
s := 0
while i <= n do
s := s + T[i]
i := i + 1
end
Jako rozmiar danych wej´sciowych bierzemy po prostu n. Ten algorytm dla danych o rozmiarze n
wykonuje n kroków – dodawa ´n postaci: s := s + T [i].
Czyli zło˙zono´s´c opisana jest funkcja t(n) = n.
Je´sli wyst ˛epuj ˛
ace w tablicy liczby s ˛
a du˙ze (przekraczaj ˛
ace 2n), musimy uwzgl ˛edni´c to w ilo´sci
wykonywanych operacji bitowych.
Edward Szczypka
4 / 1

Jagiellonian University
Theoretical
Computer Science
Zło˙zono ´s ´c pesymistyczna i ´srednia
Cz ˛esto jest tak, ze nie ka˙zde dane rozmiaru n wymagaj ˛
a takiego samego czasu oblicze ´n.
Np. niektóre algorytmy sortowania n-elementowej tablicy wykonuj ˛
a od n do n
2
kroków, w
zale˙zno´sci od tego, jak bardzo tablica była juz na wej´sciu posortowana. Innymi słowy, czas
oblicze ´n zale˙zy zwykle nie tylko od samego rozmiaru danych, ale tez od tego, jakie konkretnie
dane we´zmiemy.
Rozró˙znia si ˛e wiec zło˙zono´s´c algorytmu pesymistyczna i ´sredni ˛
a:
Zło˙zono´s´c pesymistyczna to najwi ˛eksza liczba kroków przy danych o rozmiarze n.
Zło˙zono´s´c ´srednia to ´srednia liczba kroków przy danych o rozmiarze n.
Czyli:
zło˙zono´s´c pesymistyczna to zło˙zono´s´c dla najgorszych mo˙zliwych danych,
zło˙zono´s´c ´srednia to zło˙zono´s´c dla przeci ˛etnych danych.
Edward Szczypka
5 / 1

Jagiellonian University
Theoretical
Computer Science
Zło˙zono ´s ´c pesymistyczna i ´srednia
Algorytm z przykładu 1 wykonuje n kroków niezale˙znie od tego, jakie liczby otrzymał.
Jego zło˙zono´s´c pesymistyczna jest wiec taka sama jak zło˙zono´s´c ´srednia. Oszacowanie
zło˙zono´sci ´sredniej jest cz ˛esto bardzo trudne, trzeba bowiem zna´c rozkład danych wej´sciowych
(co si ˛e trafia na wej´sciu i jak cz ˛esto). Ale zło˙zono´s´c ´srednia jest interesuj ˛
aca i wa˙zna: Istniej ˛
a
algorytmy, które maja zło˙zono´s´c ´srednia istotnie mniejsza od pesymistycznej, i dzi ˛eki temu s ˛
a
u˙zyteczne (np. quicksort).
Edward Szczypka
6 / 1

Jagiellonian University
Theoretical
Computer Science
Zło˙zono ´s ´c pami ˛eciowa
Oprócz czasochłonno´sci algorytmów rozwa˙za si ˛e tez ich pami ˛eciochłonno´sci.
Pojecie to jest opisywane przez zło˙zono´s´c pami ˛eciowa algorytmu.
Formalnie jest to funkcja s : N −→ N, która podaje ilo´s´c pami ˛eci s(n), której algorytm
potrzebuje przy danych wej´sciowych o rozmiarze n.
Tu tak˙ze mo˙zna mówi´c o zło˙zono´sci pesymistycznej i ´sredniej.
Zło˙zono´s´c czasowa jest jednak na ogół bardziej interesuj ˛
aca, m.in. dlatego, ze ogranicza
ona zło˙zono´s´c pami ˛eciowa (algorytm, który działa krótko, nie ma czasu, by zaj ˛
ac du˙zo
pami ˛eci).
Edward Szczypka
7 / 1

Jagiellonian University
Theoretical
Computer Science
Porównywanie funkcji zło˙zono ´sci
Dokładne obliczenie zło˙zono´sci algorytmu jest na ogół trudne.
Jest jednak potrzebne przy porównywaniu szybko´sci ich działania i podejmowaniu decyzji o
wyborze algorytmu przy rozwi ˛
azywaniu konkretnego problemu.
Z drugiej strony nie zwracamy uwagi na popraw ˛e szybko´sci algorytmu o stała multiplikatywna –
nie rozró˙zniamy np. miedzy zło˙zono´sciami t(n) = n oraz t
0
(
n) = 3n + 2.
przyspieszenie o stała – np. trzykrotnie –
to ró˙znica hardwareñowa (3 razy szybszy procesor),
a nie softwareñowa Chcemy jednak rozró˙zni´c funkcje działaj ˛
ace w czasie rz ˛edu log n i n,
czy tez n
2
i 2n.
Edward Szczypka
8 / 1
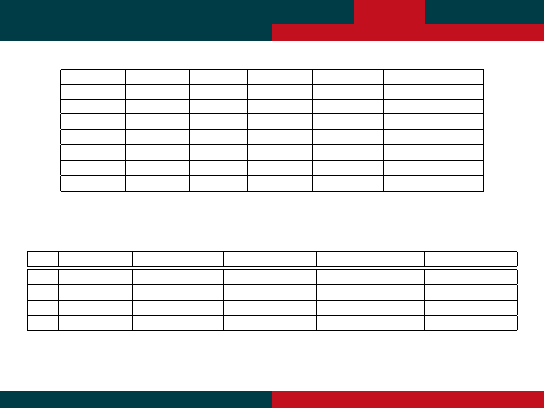
Jagiellonian University
Theoretical
Computer Science
n
10
50
100
300
1000
5n
50
250
500
1500
3000
n · log
2
n
33
282
665
2469
9966
n
2
100
2500
10000
90000
1000000
n
3
1000
125000
1000000
27000000
1000000000
2
n
1024
≈ 10
6
≈ 10
31
≈ 10
91
≈ 10
302
n!
3628800
≈ 10
65
≈ 10
161
≈ 10
623
niewyobra˙zalne
n
n
10
1
0
≈ 10
8
5
≈ 10
2
01
≈ 10
7
44
niewyobra˙zalne
oraz czasu działania programu na komputerze taktowanym 1MHz – tzn. milion operacji na
sekund ˛e:
n
10
50
100
300
1000
n
2
0.0001
sec
0.0004
sec
0.0025
sec
0.01
sec
0.9
sec
n
5
0.1
sec
3.2
sec
5.2
min
2.8
godzin
28.1
dnia
2
n
0.001
sec
1
sec
35.7
lat
≈ 4 · 10
12
stuleci
≈ 10
75
stuleci
n
n
2.8
godzin
3.3
biliony lat
≈ 10
74
stuleci
≈ 10
185
stuleci
10
728
stuleci
Wida´c tu, ze nawet przyspieszenie o stała nie pomaga
A 300 w praktycznych zastosowaniach to niewielkie dane . . .
Edward Szczypka
9 / 1

Jagiellonian University
Theoretical
Computer Science
Rz ˛
ad wielko ´sci - Notacja O
Funkcje porównujemy z uwagi na rz ˛
ad wielko´sci ˝
O zaniedbuj ˛
ac stała, tzn. przyspieszenie
hardwareñowe.
Mówimy, ze funkcja f jest rz ˛edu co najwy˙zej takiego, jak funkcja g, je´sli dla pewnej stałej c i
odpowiednio du˙zych n, zachodzi f (n) ¬ c · g(n)
Symbolicznie dla f , g : N −→ N
∃c ∈ N ∃m ∈ N ∀n m f (n) ¬ c · g(n).
Piszemy wówczas f (n) = O(g(n)) lub poprawniej f (n) ∈ O(g(n)).
Nieformalnie – funkcja f ro´snie nie szybciej ni˙z funkcja g, czyli
szybko´s´c(f ) ¬ szybko´s´c(g).
Nie zwracamy uwagi na to, co si ˛e dzieje na pocz ˛
atku
interesuj ˛
a nas tylko du˙ze liczby (czyli du˙ze rozmiary danych wej´sciowych).
Nie zwracamy tez uwagi na jednostki
mo˙zna przemno˙zy´c funkcje przez dowolna stała i to nie zmienia jej rz ˛edu.
Edward Szczypka
10 / 1

Jagiellonian University
Theoretical
Computer Science
Rz ˛
ad wielko ´sci - Notacja O
Przykład 2 Niech f (n) = 2n + 5. Jest f (n) ∈ O(n), czyli f jest rz ˛edu co najwy˙zej takiego jak
funkcja liniowa g(n) = n.
Istotnie, wystarczy wzi ˛
a´c c = 3 oraz m = 5:
wtedy dla n > 5 mamy 2n + 5 ¬ 3n.
Wszystkie funkcje postaci an + b s ˛
a rz ˛edu O(n)
– o algorytmach działaj ˛
acych w takim czasie mówimy ze s ˛
a liniowe.
Przykład 3 Funkcja 132 · n ∈ O(n
2
)
.
Istotnie dla c = 132 mamy 132 · n ¬ 132n
2
Przykład 4 Ale n
2
/
∈ O(n).
Nie ma bowiem takiej stałej c, dla której n
2
¬ c · n zachodziłoby dla prawie wszystkich n.
Gdyby taka stała była, to: n
2
¬ c · n dawałoby n ¬ c, czyli po˙z ˛
adana nierówno´s´c zachodzi tylko
dla sko ´nczenie wielu n = 0, 1, 2, . . . , c.
O funkcjach rz ˛edu O(n
2
)
mówimy, ze s ˛
a kwadratowe, a o funkcjach rz ˛edu O(n
3
)
mówimy, ze s ˛
a
sze´scienne.
Edward Szczypka
11 / 1

Jagiellonian University
Theoretical
Computer Science
Rz ˛
ad wielko ´sci - własno ´sci
Zadanie 5 Udowodnij, ˙ze;
f ∈ O(f )
je´sli f ∈ O(g) i g ∈ O(h), to f ∈ O(h),
je´sli f
1
,
f
2
∈ O(g) to f
1
+
f
2
∈ O(g),
je´sli f
1
,
f
2
∈ O(g) to f
1
· f
2
∈ O(g
2
)
Nadu˙zywaj ˛
ac troch ˛e notacji mo˙zemy pisa´c, ze:
c · O(f ) = O(c · f )
O(f ) + O(g) = O(f + g)
O(f ) · O(g) = O(f · g)
O(O(f )) = O(f )
f (n) · O(g(n)) = O(f (n) · g(n))
Edward Szczypka
12 / 1

Jagiellonian University
Theoretical
Computer Science
Rz ˛
ad wielko ´sci - wielomianów
Przykład 6 Dla wielomianów f , g rz ˛
ad ich wielko´sci wyznaczony jest przez stopie ´n:
f ∈ O(g) ⇐⇒
stopie ´n(f) = stopie ´n(g).
Ustala to hierarchi ˛e rz ˛edów funkcji:
n, n
2
,
n
3
,
n
4
, . . . ,
n
d
,
n
d +1
, . . .
Równie˙z dla stopni b ˛ed ˛
acymi dowolnymi liczbami dodatnimi mamy
n
a
∈ O(n
b
)
wtedy i tylko wtedy, gdy a ¬ b
Na przykład:
√
n ∈ O(n)
3
√
n ∈ O(
√
n)
Edward Szczypka
13 / 1

Jagiellonian University
Theoretical
Computer Science
Rz ˛
ad wielko ´sci wielomianów i funkcji wykładniczej
Przykład 7 Mamy n ∈ O(2
n
)
. Istotnie łatwo dowie´s´c indukcyjnie, ze n ¬ 2
n
.
Podobnie n
2
∈ O(2
n
)
. Wiemy juz, ze ka˙zda funkcja liniowa jest w O(2
n
)
, istnieje wiec stała c
taka, ze od pewnego miejsca 2n + 1 ¬ c · 2
n
.
Pokazemy, ze wtedy tez n
2
¬ c · 2
n
. Indukcyjnie
(
n + 1)
2
=
n
2
+
2n + 1 ¬ c · 2
n
+ (
2n + 1) ¬ c · 2
n
+
c · 2
n
=
c · 2
n+1
Analogicznie, wiedz ˛
ac juz, ze ka˙zda funkcja kwadratowa jest w O(2n), czyli ze dla pewnej stałej c
od pewnego miejsca mamy 3n
2
+
3n + 1 ¬ c · 2
n
, mo˙zemy pokaza´c indukcyjnie, ze n
3
¬ c · 2
n
.
Istotnie
(
n + 1)
3
=
n
3
+
3n
2
+
3n + 1 ¬ c · 2n + c · 2
n
=
c · 2
n+1
Ogólnie, dla dowolnego stopnia d mamy n
d
∈ O(a
n
)
, o ile tylko a > 1.
Edward Szczypka
14 / 1

Jagiellonian University
Theoretical
Computer Science
Rz ˛
ad wielko ´sci wielomianów i funkcji wykładniczej
Przykład 8 Oczywi´scie 2
n
¬ 3
n
, wiec 2
n
∈ O(3
n
)
.
Ale 3
n
/
∈ O(2
n
)
. Gdyby bowiem 3
n
¬ c · 2
n
to
3
2
n
=
3
n
2
n
¬ c
podczas gdy funkcja wykładnicza
3
2
n
ro´snie do niesko ´nczono´sci, nie mo˙ze zatem by´c
ograniczona przez stał ˛
a c.
Ogólnie dla a, b > 1, mamy a
n
∈ O(b
n
)
wtedy i tylko wtedy, gdy a ¬ b.
Przykład 9 Mamy 2
n
∈ O(n!) oraz n! ∈ O(n
n
)
.
Istotnie 2
n
¬ 2 · 1 · 2 · 3 · . . . · n = 2 · n!, bo ka˙zdy czynnik (poza pierwszym) w n! jest równy co
najmniej 2. Pokazuje to, ze 2
n
∈ O(n!). Podobnie n! = 1 · 2 · 3 · . . . · n ¬ n · n · n · . . . · n = n
n
, bo
ka˙zdy czynnik w n! jest nie wi ˛ekszy ni˙z n.
Edward Szczypka
15 / 1

Jagiellonian University
Theoretical
Computer Science
Rz ˛
ad wielko ´sci - zadania
Zadanie 10 Pokaza´c, ˙ze:
3
n
∈ O(n!)
n! /
∈ O(2
n
)
n
n
/
∈ O(n!)
log n ∈ O(
√
n)
log n ∈ O(
3
√
n)
Uogólnij, tak jak umiesz, powy˙zsze fakty.
Przykład 11 Czy
√
n ∈ O(
n
log n
)
P
n
i=1
i ∈ O(n)
P
n
i=1
i ∈ O(n
2
)
n
2
∈ O(
P
n
i=1
i)
P
n
i=1
i
2
∈ O(n
2
)
Edward Szczypka
16 / 1

Jagiellonian University
Theoretical
Computer Science
Zło˙zono ´s ´c algorytmów raz jeszcze
Do czego u˙zywamy "O du˙zego":
"O du˙ze" jest potrzebne do opisywania zło˙zono´sci algorytmów
by pomin ˛
a´c zb ˛edne (i trudne do policzenia. . . ) szczegóły i skupi´c si ˛e na rz ˛edzie
funkcji
zwykle wiec podajemy zło˙zono´s´c algorytmu za pomoc ˛
a "O du˙zego", najdokładniej jak
potrafimy
np. o algorytmie sumowania liczb powiemy, ze ma zło˙zono´s´c O(n) – a nie O(n
2
)
, cho´c to
tez byłaby prawda.
Przykłady:
najlepsze algorytmy sortowania maja zło˙zono´s´c O(n log n), gdzie n jest liczba
sortowanych elementów
popularne algorytmy sortowania – O(n
2
)
algorytm Floyda znajduj ˛
acy wszystkie najkrótsze ´scie˙zki w danym grafie maj ˛
acym n
wierzchołków – O(n
3
)
algorytm wyszukiwania elementu w posortowanej bazie danych zawieraj ˛
acej n elementów
– O(log n).
Edward Szczypka
17 / 1

Jagiellonian University
Theoretical
Computer Science
Zło˙zono ´s ´c algorytmów raz jeszcze
Powszechnie uwa˙za si ˛e, ze praktycznie u˙zyteczne s ˛
a algorytmy o zło˙zono´sci
wielomianowej lub lepszej, np.:
log n,
3
√
n,
√
n, n, n log n, n
√
n, n
2
,
n
3
,
n
k
Algorytmy o zło˙zono´sci wykładniczej lub gorszej, np.: 2
n
,
n!, n
n
uwa˙za si ˛e za
niepraktyczne.
Czasem rozwa˙za si ˛e w praktyce (zwłaszcza w kryptografii przy łamaniu kodów) algorytmy
o zło˙zono´sci n
log n
, która nie jest wielomianowa, ale ro´snie znacznie wolniej ni˙z 2
n
.
Jeden z centralnych problemów współczesnej informatyki (P = NP) dotyczy zło˙zono´sci
algorytmów.
Zadanie 12 Udowodnij, ze n
log n
/
∈ 2O(n
k
)
, dla ˙zadnego stałego k , ale n
log n
∈ O(a
n
)
dla
dowolnego a > 1.
Edward Szczypka
18 / 1

Jagiellonian University
Theoretical
Computer Science
spis
Edward Szczypka
19 / 1

Jagiellonian University
Theoretical
Computer Science
Definicja rekurencyjna
nieformalnie – taka definicja, która odwołuje si ˛e do samej siebie
ale trzeba tu uwa˙za´c, by odwołanie było do instancji o mniejszej komplikacji
zwykle chodzi o ci ˛
ag ha
0
,
a
1
,
a
2
,
a
3
, . . .i
,
dla którego przepis na element a
n
wykorzystuje jaki(e)´s poprzedni(e) element(y):
a
n−1
,
a
n−2
, . . .
itp.
pocz ˛
atkowy element (lub kilka pocz ˛
atkowych) musza by´c zadane konkretnie
˙zeby było od czego zacz ˛
a´c
zwykle definicja rekurencyjna odwołuje si ˛e do jednego lub kilku poprzednich elementów,
ale mo˙ze tez odwoływa´c si ˛e do wszystkich poprzednich
Edward Szczypka
20 / 1

Jagiellonian University
Theoretical
Computer Science
Definicja rekurencyjna - przykłady
Przykład 13 Silnia, tzn. ci ˛
ag 0!, 1!, 2!, 3!, 4!, . . . mo˙ze by´c zadany rekurencyjnie jako:
s
0
=
1
s
n
=
n · s
n−1
dla n > 1
Mo˙zna te˙z zada´c go jako:
s
0
=
1
s
n+1
= (
n + 1) · s
n
dla n > 0
Poniewa˙z pierwszy wyraz jest zadany, to mo˙zemy kolejno oblicza´c:
s
0
=
1
s
1
=
1 · s
0
=
1 · 1 = 1
s
2
=
2 · s
1
=
1 · 2 = 2
s
3
=
3 · s
2
=
3 · 2 = 6
s
4
=
4 · s
3
=
4 · 6 = 24
. . .
Edward Szczypka
21 / 1

Jagiellonian University
Theoretical
Computer Science
Definicja rekurencyjna - przykłady
Zadanie 14 Jaki ci ˛
ag jest zdefiniowany poprzez mała modyfikacje w definicji silni?
s
0
=
0
s
n
=
n · s
n−1
dla n > 1
A co definiuj ˛
a nast ˛epuj ˛
ace okre´slenia:
s
0
=
1
2
s
n
=
n · s
n−1
dla n > 1
oraz
s
0
=
1
s
n
=
n · s
n−2
dla n > 2
W ostatnim przypadku wida´c, ze poniewa˙z odwołanie jest dwa wyrazy wstecz, to juz wyliczenie
pierwszego wyrazu s
1
staje si ˛e niemo˙zliwe.
Edward Szczypka
22 / 1

Jagiellonian University
Theoretical
Computer Science
Ci ˛
ag arytmetyczny
Przykład 15 W ci ˛
agu zadanym poprzez równania:
s
0
=
0
s
n
=
s
n−1
+
2
dla n 1
łatwo rozpozna´c kolejne liczby parzyste:
s
n
=
2n
Ogólnie ci ˛
ag zadany poprzez ustalenie a
0
oraz zadanie
a
n
=
a
n−1
+
r
to tzw. ci ˛
ag arytmetyczny. Jego n-ty wyraz dany jest wzorem:
a
n
=
a
0
+
n · r
Aby to uzasadni´c, pokazujemy indukcyjnie, ze:
a
0
+
0 · r = a
0
jest rzeczywi´scie zerowym wyrazem ci ˛
agu
oraz
a
0
+
n · r = (a
0
+ (
n − 1)r ) + r = a
n−1
+
r = a
n
Edward Szczypka
23 / 1

Jagiellonian University
Theoretical
Computer Science
Ci ˛
ag geometryczny
Przykład 17 W ci ˛
agu zadanym poprzez równania:
s
0
=
1
s
n
=
2 · s
n−1
dla n 1
łatwo rozpozna´c kolejne pot ˛egi liczy 2:
s
n
=
2
n
Ogólnie ci ˛
ag zadany poprzez ustalenie a
0
oraz zadanie
a
n
=
q · a
n−1
to tzw. ci ˛
ag geometryczny. Jego n-ty wyraz dany jest wzorem:
a
n
=
a
0
· q
n
Aby to uzasadni´c, pokazujemy indukcyjnie, ze:
a
0
· q
0
=
a
0
· 1 = a
0
jest rzeczywi´scie zerowym wyrazem ci ˛
agu
oraz
a
0
· q
n
= (
a
0
· q
n−1
) ·
q = a
n−1
· q = a
n
Edward Szczypka
24 / 1
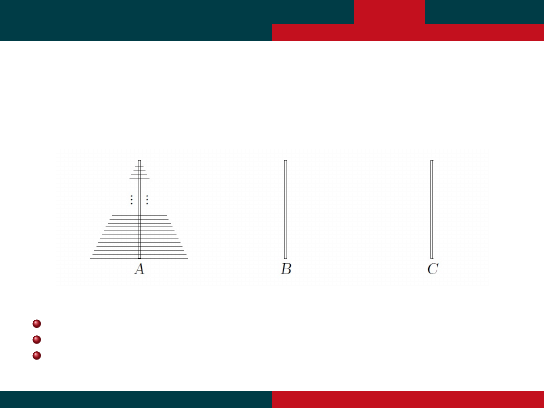
Jagiellonian University
Theoretical
Computer Science
Wie˙za Hanoi
Zadanie 18 (E.Lucas, 1883) U zarania czasu Bóg umie´scił 64 złote kr ˛
a˙zki na jednej z trzech
diamentowych iglic tak, ze kr ˛
a˙zki wy˙zej umieszczone miały mniejsze promienie.
Nast ˛epnie Bóg polecił grupie mnichów przeło˙zenie tych kr ˛
a˙zków na trzecia iglice (C), ale tak by:
w jednym ruchu przenosi´c tylko jeden kr ˛
a˙zek,
kr ˛
a˙zek wi ˛ekszy nigdy nie mo˙ze le˙ze´c na kr ˛
a˙zku mniejszym,
mo˙zna posługiwa´c si ˛e iglica B.
Mnisi pracuj ˛
a od zarania dziejów dzie ´n i noc . . . Ile czasu im to zajmie?
Edward Szczypka
25 / 1

Jagiellonian University
Theoretical
Computer Science
Wie˙ze Hanoi -cd
Aby obliczy´c wystarczaj ˛
ac ˛
a ilo´s´c ruchów do wykonania zadania, zanalizujmy najpierw małe
przypadki:
Łatwo zauwa˙zy´c, ze dla 1 kr ˛
a˙zka potrzebny jest jeden ruch: A −→ C
Podobnie dla dwu kr ˛
a˙zków mo˙zemy post ˛
api´c: A −→ B, A −→ C, B −→ C
Przy 3 kr ˛
a˙zkach post ˛epujemy tak:
najpierw przenosimy dwa górne kr ˛
a˙zki na iglice B posługuj ˛
ac si ˛e iglica C:
A −→ C, A −→ B, C −→ B
przenosimy najwi ˛ekszy kr ˛
a˙zek z A na C: A −→ C
przenosimy kr ˛
a˙zki z B na C posługuj ˛
ac si ˛e iglic ˛
a A: B −→ A, B −→ C, A −→ C
co pokazuje, ze wystarcza tu 7 ruchów. Czy juz wiesz jak rozwi ˛
aza´c to zadanie w ogólno´sci (dla
n kr ˛
a˙zków)?
Edward Szczypka
26 / 1

Jagiellonian University
Theoretical
Computer Science
Mamy wiec równanie rekurencyjne
H
1
=
1
H
n
=
2 · H
n−1
+
1
dla n > 2
bardzo podobne do ci ˛
agu geometrycznego.
Mo˙zemy policzy´c kilka jego wyrazów:
1, 3, 7, 15, 31, 63, 127, . . .
i rozpozna´c w nim ci ˛
ag pot ˛eg dwójki zmniejszonych o 1.
Ale czy rzeczywi´scie H
n
=
2
n
− 1?
I znów, aby si ˛e upewni´c, ˙ze nasze odgadni ˛ecie było poprawne, sprawdzamy indukcyjnie, ˙ze:
2 · H
n−1
+
1 = 2 · (2
n−1
− 1) + 1 = 2 · 2
n−1
− 2 + 1 = 2
n
− 1 = H
n
co oznacza, ze rzeczywi´scie ci ˛
ag 2
n
− 1 spełnia równanie rekurencyjne, którym zadany jest ci ˛
ag
H
n
.
A wiec H
64
=
2
64
− 1 ≈ 100 000 000 000 000 000 000, co przy przenoszeniu jednego kr ˛
a˙zka na
sekund ˛e zajmie ponad 3 000 000 000 000 a przenosz ˛
ac te kr ˛
a˙zki "komputerem" 3GHz potrzeba
b ˛edzie i tak ponad tysi ˛
ac lat . . .
Edward Szczypka
27 / 1

Jagiellonian University
Theoretical
Computer Science
Wie˙ze Hanoi - cd
Co zrobi´c z funkcj ˛
a/ci ˛
agiem zadanym za pomoc ˛
a definicji rekurencyjnej:
próbowa´c znale´z´c definicje lub algorytm nierekurencyjny – mo˙ze si ˛e okaza´c
efektywniejszy w obliczeniach
oblicza´c za pomoc ˛
a programu rekurencyjnego
ale wtedy nie wida´c wprost jaka zło˙zono´s´c obliczeniowa ma taki program/procedura.
Jak znale´z´c definicje nierekurencyjna:
znajdowanie nierekurencyjnej definicji dla ci ˛
agu zadanego rekurencyjnie to rozwi ˛
azywanie
równania rekurencyjnego,
jest to w ogólno´sci trudny problem
cz ˛esto nie ma ˙zadnej rozs ˛
adnej definicji nierekurencyjnej
istniej ˛
a metody rozwi ˛
azywania równa ´n rekurencyjnych, ale tylko dla pewnych
szczególnych rodzajów
czasem mo˙zna spróbowa´c odgadn ˛
a´c definicje nierekurencyjna i nast ˛epnie udowodni´c, ˙ze
rzeczywi´scie opisuje ona ten sam ci ˛
ag.
Taki dowód robi si ˛e za pomoc ˛
a indukcji.
Edward Szczypka
28 / 1

Jagiellonian University
Theoretical
Computer Science
Ci ˛
ag Fibonacci’ego
Ci ˛
ag Fibonacciñego zadany nast ˛epuj ˛
aco:
f
0
=
1
f
1
=
1
f
n
=
f
n−1
+
f
n−2
dla n > 2
a jego pierwsze wyrazy to:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, . . .
Jak odgadnac wzór na ogólny wyraz ci ˛
agu?
Je´sli nie mo˙zna odgadn ˛
a´c, to jak oszacowa´c szybko´s´c wzrostu tego ci ˛
agu?
Czy ro´snie on wielomianowo czy raczej wykładniczo?
Pierwsze pytanie – póki co – wydaje si ˛e do´s´c beznadziejne.
Edward Szczypka
29 / 1

Jagiellonian University
Theoretical
Computer Science
Ci ˛
ag Fibonacci’ego – szacowanie wzrostu
Czy f
n
ro´snie wielomianowo? tzn. czy f
n
∈ O(n
k
)
? Zauwa˙zmy, ˙ze dla ci ˛
agu an zachowuj ˛
acego
si ˛e jak wielomian stopnia k , nowo zdefiniowany ci ˛
ag:
a
0
n
=
a
n+1
− a
n
zachowuje si ˛e jak (n + 1)
k
− n
k
– wielomian stopnia k − 1.
podobnie ci ˛
ag a
00
dany przez
a
00
n
=
a
0
n+1
− a
0
n
zachowuje si ˛e jak wielomian stopnia k − 2, i post ˛epuj ˛
ac tak dalej, otrzymaliby´smy, ˙ze ci ˛
ag ró˙znic
kolejnych wyrazów w
a
(
i)
n
=
a
(
i−1)
n+1
− a
(
i−1)
n
zachowuje si ˛e jak wielomian stopnia k − i.
Ostatecznie, gdyby ci ˛
ag a
n
zachowywał si ˛e jak wielomian stopnia k to ci ˛
ag a
(
k )
n
byłby stały.
A jak wygl ˛
adaj ˛
a takie ci ˛
agi ró˙znic dla ci ˛
agu Fibonacciego?
Edward Szczypka
30 / 1
Jagiellonian University
Theoretical
Computer Science
Ci ˛
ag Fibonacci’ego – szacowanie wzrostu
Badaj ˛
ac kolejne ci ˛
agi ró˙znic wywiedzione z Ciagu Fibonacciñego dostajemy:
f
0
n
=
f
n+1
− f
n
= (
f
n
+
f
n−1
) −
f
n−1
czyli
f
n
f
0
f
1
f
2
f
4
f
4
f
5
f
6
f
7
f
8
. . .
f
0
n
f
0
f
1
f
2
f
4
f
4
f
5
f
6
f
7
. . .
f
00
n
f
0
f
1
f
2
f
4
f
4
f
5
f
6
. . .
f
(
3)
n
f
0
f
1
f
2
f
4
f
4
f
5
. . .
.
.
.
i widzimy, ze ci ˛
ag ten odradza si ˛e sam z siebie
nigdy tym samym nie prowadz ˛
ac do ci ˛
agu stałego.
Nie jest to ´scisły dowód, ze f
n
nie mo˙ze by´c rz ˛edu O(n
k
)
.
Sugeruje jednak taka mo˙zliwo´s´c.
Mo˙ze wiec 2
n
∈ O(f
n
)
lub cho´cby a
n
∈ O(f
n
)
dla pewnego a > 1?
Edward Szczypka
31 / 1

Jagiellonian University
Theoretical
Computer Science
Spróbujmy pokaza´c, ˙ze 2
n
∈ O(f
n
)
tzn., 2
n
¬ c · f
n
.
Dowód taki indukcyjnie szedłby nast ˛epuj ˛
aco:
c · f
n
=
c · f
n−1
+
c · f
n−2
>
2
n−1
+
2
n−2
=
2
n−2
(
2 + 1) = 3 · 2
n−2
=
3
4
· 2
n
a chcieliby´smy, by c · f
n
>
2
n
. Mo˙ze wiec f
n
nie ro´snie tak szybko jak 2
n
, a raczej jak a
n
dla
jakiego´s 1 < a < 2?
Pojawiaj ˛
aca si ˛e liczba 3 sugeruje, ze mo˙ze a =
3
2
byłoby dobrym wyborem?
Sprawdzamy
c · f
n
=
c · f
n−1
+
c · f
n−2
3
2
n−1
+
3
2
n−2
=
3
n−1
2
n−1
+
3
n−2
2
n−2
=
3
n−1
+
2 · 3
n−2
2
n−1
=
5 · 3
n−2
2
n−1
Gdyby wiec
5·3
n−2
2
n−1
3
2
n
, to mogliby´smy zako ´nczy´c dowód naszego przypuszczenia, ˙ze
3
2
n
∈ O(f
n
)
z sukcesem. Po˙z ˛
adana nierówno´s´c:
5·
n−2
2
n−1
3
n
2
n
redukuje si ˛e wszak˙ze do równowa˙znej jej, prawdziwej nierówno´sci:
5
1
3
2
2
=
9
2
co ko ´nczy dowód.
Edward Szczypka
32 / 1

Jagiellonian University
Theoretical
Computer Science
Ci ˛
ag Fibonacci’ego – szacowanie wzrostu
Spróbujmy rozwi ˛
aza´c równanie ci ˛
agu Fibonacciñego. Chwilowo zaniedbamy ile wynosz ˛
a
pocz ˛
atkowe wyrazy f
0
i f
1
i skupimy si ˛e na wzorze:
f
n
=
f
n−1
+
f
n−2
Przypu´s´cmy przez chwile, ze rozwi ˛
azaniem tego równania jest jaki´s ci ˛
ag geometryczny c · x
n
.
Wtedy
c · x
n
=
c · x
n−1
+
c · x
n−2
co, przy zało˙zeniu, ze c, x 6= 0 pozwala na wydzielenie przez c · x
n−2
i doprowadza do równania
kwadratowego:
x
2
=
x + 1
które ma dwa rozwi ˛
azania:
x
1
=
1 +
√
5
2
i x
2
=
1 −
√
5
2
Edward Szczypka
33 / 1

Jagiellonian University
Theoretical
Computer Science
Który wiec z ci ˛
agów miałby by´c szukanym ci ˛
agiem Fibonacciego?
Zauwa˙zmy, ˙ze gdy ci ˛
agi x
n
i y
n
nadaj ˛
a si ˛e na rozwi ˛
azania, to i ci ˛
ag c
1
· x
n
+
c
2
· y
n
nadaje si ˛e na
takie rozwi ˛
azanie i to przy zupełnie dowolnych stałych c
1
,
c
2
(ich dokładne ustalenie, zale˙ze´c
b ˛edzie od tymczasowo zaniedbanych warto´sci wyrazów pocz ˛
atkowych).
A zatem naszym rozwi ˛
azaniem mo˙ze by´c:
f
n
=
c
1
· x
n
1
+
c
2
x
n
2
Aby wyznaczy´c stałe c
1
,
c
2
zauwa˙zmy, ze musz ˛
a one spełnia´c układ równa ´n:
f
0
=
c
1
+
c
2
f
1
=
c
1
· x
1
+
c
2
· x
2
co po rozwi ˛
azaniu daje:
c
1
=
f
1
− f
0
x
2
x
1
− x
2
=
1 −
1−
√
5
2
1+
√
5
2
−
1−
√
5
2
=
1
√
5
1 +
√
5
2
c
2
=
f
1
− f
0
x
1
x
2
− x
1
=
1 −
1+
√
5
2
1−
√
5
2
−
1+
√
5
2
= −
1
√
5
1 −
√
5
2
i ostatecznie
f
n
=
1
√
5
"
1 +
√
5
2
n+1
−
1 −
√
5
2
n+1
#
Edward Szczypka
34 / 1

Jagiellonian University
Theoretical
Computer Science
Ci ˛
ag Fibonacciego – szacowanie wzrostu
Zadanie 18 Zweryfikuj, ˙ze
f
n
=
1
√
5
"
1 +
√
5
2
n+1
−
1 −
√
5
2
n+1
#
jest ci ˛
agiem Fibonacciego.
Zadanie 19 Rozwi ˛
a˙z równanie rekurencyjne:
s
0
=
3
s
1
=
3
s
n
=
s
n−1
+
2s
n−2
poprzez rozwi ˛
azanie równania kwadratowego x
2
=
x + 2, a nast ˛epnie wyznaczenie
odpowiednich stałych c
1
,
c
2
.
Edward Szczypka
35 / 1

Jagiellonian University
Theoretical
Computer Science
Aby rozwi ˛
aza´c równanie rekurencyjne
s
n
=
a · s
n−1
+
b · s
n−2
rozwi ˛
azujemy równanie kwadratowe
x
2
=
a · x + b
i je´sli ma ono dwa pierwiastki x
1
,
x
2
, to rozwi ˛
azaniem jest
s
n
=
c
1
· x
n
1
+
c
2
· x
n
2
ze stałymi
c
1
=
s
1
− s
0
x
2
x
1
− x
2
c
2
=
s
1
− s
0
x
1
x
2
− x
1
Gdy równanie x
2
=
ax + b ma tylko jeden pierwiastek x
0
(podwójny, gdy a
2
=
4b), to
rozwi ˛
azaniem jest
s
n
=
c
1
· x
n
0
+
c
2
· n · x
n
ze stałymi wyznaczonymi, jak poprzednio, poprzez dwa pierwsze wyrazy pocz ˛
atkowe:
c
1
=
s
0
c
2
=
s
1
− s
0
x
0
x
0
Edward Szczypka
36 / 1

Jagiellonian University
Theoretical
Computer Science
Przykład 19 A co si ˛e dzieje je´sli równanie x
2
=
ax + b nie ma rozwi ˛
aza ´n?
Np. dla ciagu g
n
=
g
n−1
− g
n−2
.
Przecie˙z, gdy ustalimy dwa pierwsze wyrazy pocz ˛
atkowe np. g
0
=
2 i g
2
=
3 dostaniemy ci ˛
ag:
3, 5, 2, −3, −5, −2, 3, 5, 2, −3, −5, −2, 3, 5, 2, −3, −5, −2, 3, 5, 2, . . .
W istocie równanie x
2
=
ax + b ma wtedy dwa rozwi ˛
azania w´sród liczb zespolonych, i mo˙zemy
post ˛epowa´c analogicznie jak w przypadku dwu rozwi ˛
aza ´n rzeczywistych.
Zadanie 20 Rozwi ˛
a˙z równanie rekurencyjne
s
0
=
1
s
1
=
2
s
n
=
2s
n−1
− s
n−2
Czy rozwi ˛
azanie tez cechuje si ˛e wzrostem wykładniczym?
Zadanie 21 Rozwi ˛
a˙z równanie rekurencyjne
s
0
=
1
s
1
=
1
s
n
=
s
n−1
− 2 · s
n−2
Czy rozwi ˛
azanie ma wzrost wykładniczy? a mo˙ze jest okresowe jak w przykładzie 19?
Edward Szczypka
37 / 1

Jagiellonian University
Theoretical
Computer Science
spis
Edward Szczypka
38 / 1

Jagiellonian University
Theoretical
Computer Science
Proste zasady zliczania
Zasada nr 1:
Je´sli zbiory A i B s ˛
a rozł ˛
aczne, to kA ∪ Bk = kAk + kBk
Ta zasada pozwala rozpatrywa´c osobno i nast ˛epnie doda´c wszelkie odr ˛ebne przypadki.
Zasada nr 2:
Dla dowolnych zbiorów A i B mamy kA × Bk = kAk · kBk.
Ta zasada pozwala zlicza´c pary (zestawienia) niezale˙znych obiektów
Edward Szczypka
39 / 1

Jagiellonian University
Theoretical
Computer Science
Proste zasady zliczania
Przykład 24 W pewnym niewielkim ksi ˛estwie tablice rejestracyjne zawieraj ˛
a zawsze jedna liter ˛e i
jedna cyfr ˛e.
Liter jest 26, cyfr jest 10.
Zgodnie z zasada nr 2 liczba mo˙zliwych tablic rejestracyjnych to 26 · 10 = 260.
Przykład 25: Niewielkie ksi ˛estwo nieco si ˛e rozrosło i oprócz tablic takich, jak opisano wcze´sniej,
s ˛
a potrzebne jeszcze tablice zawieraj ˛
ace dwie litery i dwie cyfry.
Zgodnie z zasada nr 1 rozpatrujemy osobno dwa przypadki:
tablice typu LC oraz tablice typu LLCC.
Dla przypadku LC mamy 26 · 10 = 260 mo˙zliwych tablic.
Dla przypadku LLCC mamy 26 · 26 · 10 · 10 = 67600 mo˙zliwych tablic.
Zgodnie z zasada nr 1 mamy razem 260 + 67600 = 67860 mo˙zliwych tablic. Tu wa˙zne jest to, ze
owe dwa przypadki nie zaz ˛ebiaj ˛
a si ˛e, tzn. ˙zadna tablica typu LC nie jest tablica typu LLCC.
Edward Szczypka
40 / 1

Jagiellonian University
Theoretical
Computer Science
Zliczanie funkcji
Ile jest funkcji
ze zbioru k -elementowego X = {x
1
,
x
2
, . . . ,
x
k
}
do zbioru n-elementowego Y = {y
1
,
y
2
, . . . ,
y
n
}?
Liczymy sposoby przyporzadkowania:
elementowi x
1
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y – na n sposobów
elementowi x
2
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y – na n sposobów
. . .
elementowi x
k
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y – na n sposobów
Zatem, korzystaj ˛
ac z Zasady nr 1, widzimy ze wszystkich takich przyporz ˛
adkowa ´n jest
n · n · . . . · n = n
k
.
Ka˙zda funkcje postaci X −→ Y , mo˙zemy uto˙zsami´c z kX k = k elementowym ci ˛
agiem, którego
wyrazami s ˛
a elementy zbioru Y , a zatem z elementem produktu X × X × . . . × X = X
k
.
Cz ˛esto zbiór funkcji postaci X −→ Y oznaczany jest jako Y
X
. Wtedy
kX
Y
k = kX k
kY k
Edward Szczypka
41 / 1

Jagiellonian University
Theoretical
Computer Science
Zliczanie funkcji
Przykład 27: Ile jest 8-mio cyfrowych tablic rejestracyjnych?
Ka˙zda taka tablica to ci ˛
ag 8-mio elementowy. A zatem liczb takich jest 10
8
.
Przykład 4 Ile jest 8-mio cyfrowych liczb naturalnych w zapisie dziesi ˛etnym?
Tu, w odró˙znieniu od poprzedniego przykładu, zabroniona jest sytuacja, w której na pocz ˛
atku
wyst ˛epuj ˛
a nieznacz ˛
ace zera
(chyba, ˙ze jest w ogóle tylko jedno zero, tzn. rozwa˙zamy liczb ˛e 0).
A zatem 10
8
to ilo´s´c liczb co najwy˙zej 8-cyfrowych.
Spo´sród wszystkich liczb co najwy˙zej 8-mio cyfrowych musimy wyrzuci´c te, które maja co
najwy˙zej 7 cyfr i dostaniemy wtedy,
˙ze liczb o dokładnie 8-miu cyfrach jest
10
8
− 10
7
= (
10 − 1) · 10
7
=
9 · 10
7
.
Edward Szczypka
42 / 1

Jagiellonian University
Theoretical
Computer Science
Zliczanie bijekcji
Aby pomi ˛edzy dwoma zbiorami sko ´nczonymi istniała jakakolwiek bijekcja zbiory te musz ˛
a mie´c
tyle samo elementów.
Ile jest wobec tego bijekcji pomiedzy dwoma zbiorami n-elementowymi X = {x
1
,
x
2
, . . . ,
x
n
} i
Y = {y
1
,
y
2
, . . . ,
y
n
}?
Liczymy sposoby przyporz ˛
adkowania:
elementowi x
1
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y na n sposobów
elementowi x
2
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y na n + 1 sposobów
gdy˙z jeden element juz jest wykorzystany, a injektywno´s´c zabrania wykorzystania go
ponownie
elementowi x
3
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y na n − 2 sposoby,
gdy˙z dwa elementy s ˛
a ju˙z wykorzystane, a injektywno´s´c zabrania . . .
. . .
elementowi x
n−1
mo˙zemy przyporzadkowac jeden z elementów zbioru Y na 2 sposoby,
gdy˙z n − 2 elementy zbioru Y zostały juz wykorzystane,
wreszcie dla elementu x
n
nie mamy juz wcale wyboru, mo˙zemy (i musimy)
przyporzadkowa´c mu pozostały, niewykorzystany jeden element, czyli jest tylko jeden taki
sposób
a zatem takich sposobów jest
n · (n − 1) · (n − 2) · . . . · 2 · 1
Edward Szczypka
43 / 1

Jagiellonian University
Theoretical
Computer Science
Zliczanie bijekcji cd (permutacje)
W szczególno´sci policzyli´smy liczb ˛e bijekcji zbioru X = {x
1
,
x
2
, . . . ,
x
n
} w siebie. Takie
auto-bijekcje nazywamy permutacjami zbioru X .
Niech n! oznacza liczb ˛e permutacji zbioru n-elementowego
Czy rzeczywi´scie policzyli´smy liczb ˛e permutacji ka˙zdego zbioru sko ´nczonego?
A co ze zbiorem pustym?
łatwo sprawdzi´c formalnie, ze
∅ ⊆ ∅ × ∅ jest nie tylko funkcj ˛
a ∅ : ∅ −→ ∅
ale i bijekcj ˛
a
i jest to jedyna bijekcja ∅ −→ ∅
A zatem
0! = 1
1! = 1
n! = 1 · 2 · 3 · . . . · (n − 1) · n
wyra˙za liczb ˛e permutacji zbioru n-elementowego.
Edward Szczypka
44 / 1

Jagiellonian University
Theoretical
Computer Science
Zliczanie inijekcji (wariacji bez powtórze ´
n)
Ile jest injekcji
ze zbioru k-elementowego X = {x
1
,
x
2
, . . . ,
x
k
}
do zbioru n-elementowego Y = {y
1
,
y
2
, . . . ,
y
n
}?
Liczymy sposoby przyporz ˛
adkowania:
elementowi x
1
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y na n sposobów
elementowi x
2
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y na n − 1 sposobów,
gdy˙z jeden element ju˙z jest wykorzystany, a injektywno´s´c zabrania wykorzystania go
ponownie
elementowi x
3
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y na n − 2 sposoby,
. . .
elementowi x
k
mo˙zemy przyporz ˛
adkowa´c jeden z elementów zbioru Y na n − (k − 1)
sposobów
Zatem, korzystaj ˛
ac z Zasady nr 2 widzimy, ze wszystkich takich przyporz ˛
adkowa ´n jest
n · (n − 1) · (n − 2) . . . · (n − k + 2) · (n − k + 1) =
n!
(
n − k )!
Edward Szczypka
45 / 1

Jagiellonian University
Theoretical
Computer Science
Zliczanie funkcji
Zadanie 27 Na ka˙zde z 16-tu województw trzeba wydelegowa´c jednego z 20-tu specjalistów
zarz ˛
adzaj ˛
acych spisem powszechnym w tym województwie. Ka˙zde województwo ma mie´c
innego specjalist ˛e. Na ile sposobów mo˙zna to zrobi´c?
Zadanie 28 128-miu uczestnikom pewnej konferencji informatycznej przygotowano konta
komputerowe, gdzie ID s ˛
a 8-znakowe i utworzone wył ˛
acznie z liter a, b. Przydzielono je pó´zniej
losowo ˚
U na ile sposobów było to mo˙zliwe?
Zadanie 29 Ile jest 8-mio cyfrowych liczb (w systemie dzisi ˛etnym), w których ˙zadna cyfra si ˛e nie
powtarza?
Zadanie 30 Ile jest co najwy˙zej 10-cio cyfrowych liczb (w systemie dziesi ˛etnym), w których
˙zadna cyfra si ˛e nie powtarza?
Edward Szczypka
46 / 1
Document Outline
Wyszukiwarka
Podobne podstrony:
lecture 05
Feynman Lectures on Physics Volume 1 Chapter 05
lecture slides 05
Lecture 04 05 06 C Primer New
Lecture 04 05 06 C Primer New
IR Lecture1
podrecznik 2 18 03 05
regul praw stan wyjątk 05
uml LECTURE
lecture3 complexity introduction
05 Badanie diagnostyczneid 5649 ppt
Podstawy zarządzania wykład rozdział 05
05 Odwzorowanie podstawowych obiektów rysunkowych
05 Instrukcje warunkoweid 5533 ppt
więcej podobnych podstron