- 18 -
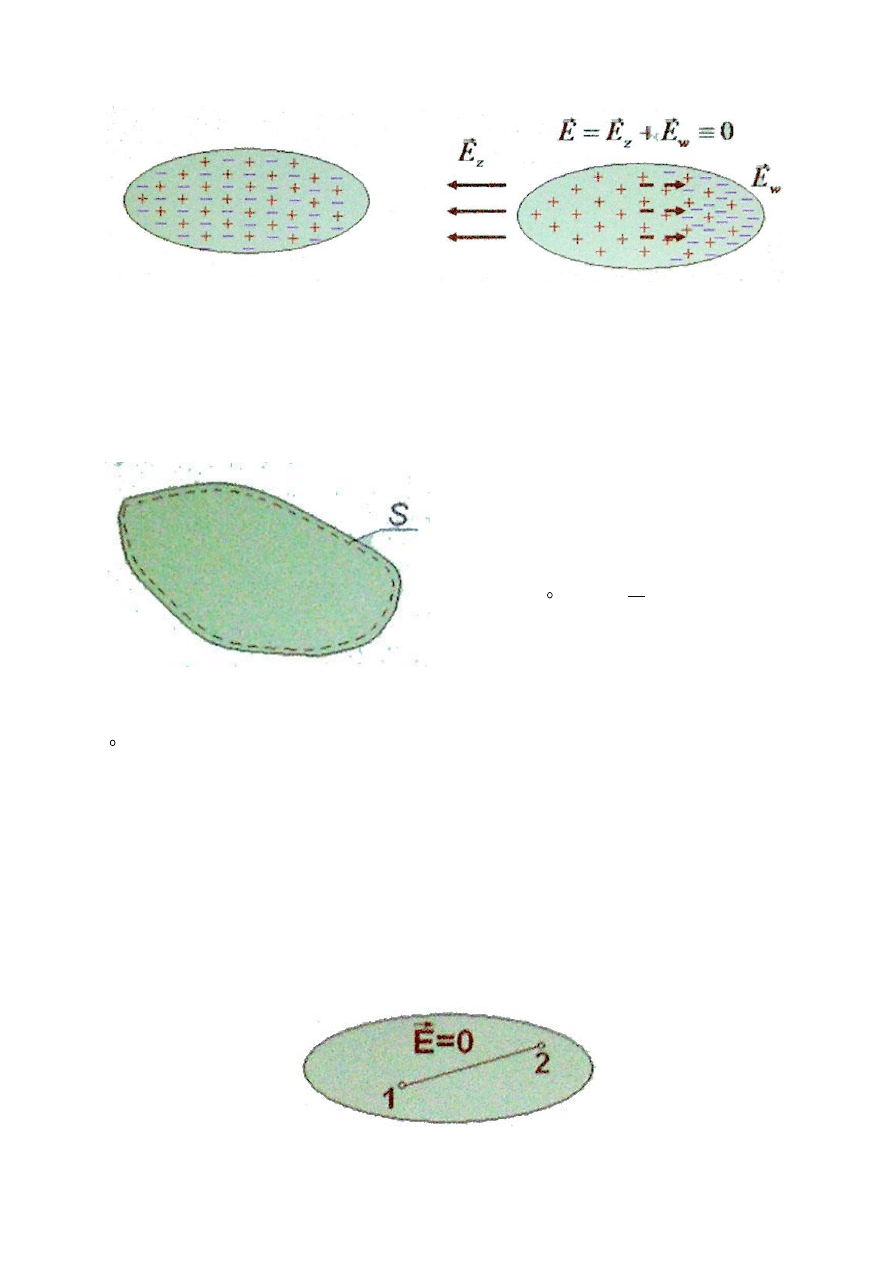
Przewodnik w równowadze Przewodnik w zewnętrznym polu elektrycznym
Ładunek w przewodniku
Udowodnimy, na podstawie prawa Gaussa, że dowolny ładunek wprowadzony do
przewodnika zawsze musi się zbierać na jego powierzchni.
Pomyslaną powierzchnią S wybieramy tuż
poniżej realnej powierzchni przewodnika
0
Q
S
d
E
V
W równowadze, w dowolnym pkt. powierzchni S, pole elektryczne jest równe 0.
0
0
Q
dS
E
V
Ponieważ pomyślaną powierzchnię S możemy wybrac dowolnie stad w każdym
elemencie objętości Q=0
Stąd ładunek wprowadzony do przewodnika musi się zawsze zbierać na jego
powierzchni.
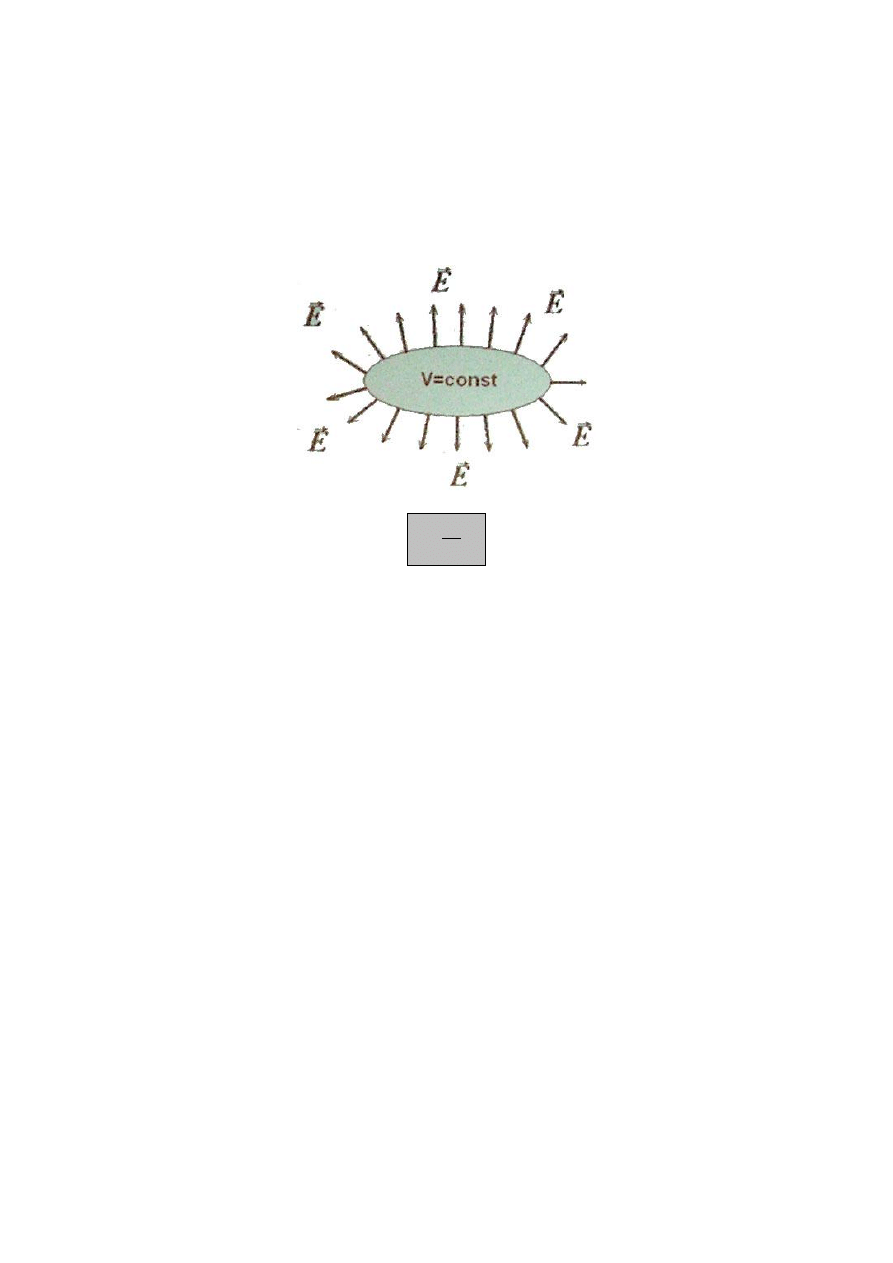
Potencjał elektryczny przewodnika
Znając pole elektryczne w przewodniku możemy obliczyć jego potencjał.
- 19 -
const
V
V
r
d
E
V
V
V
1
2
2
1
1
2
0
Przewodnik stanowi obszar stałego potencjału. Pole elektryczne jest zawsze
prostopadłe do powierzchni stałego potencjału, czyli jest zawsze prostopadła do
powierzchni przewodnika.
n
E
0
- 20 -
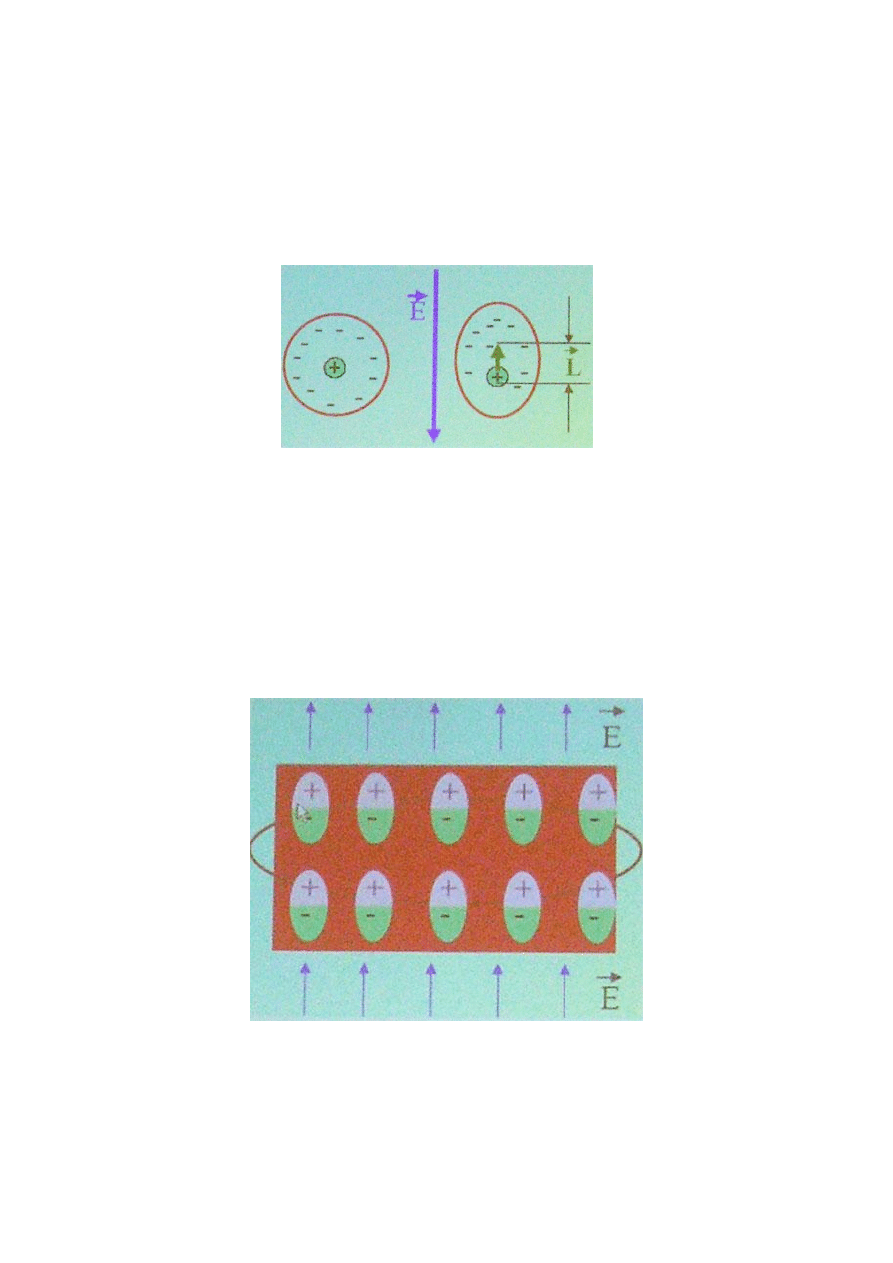
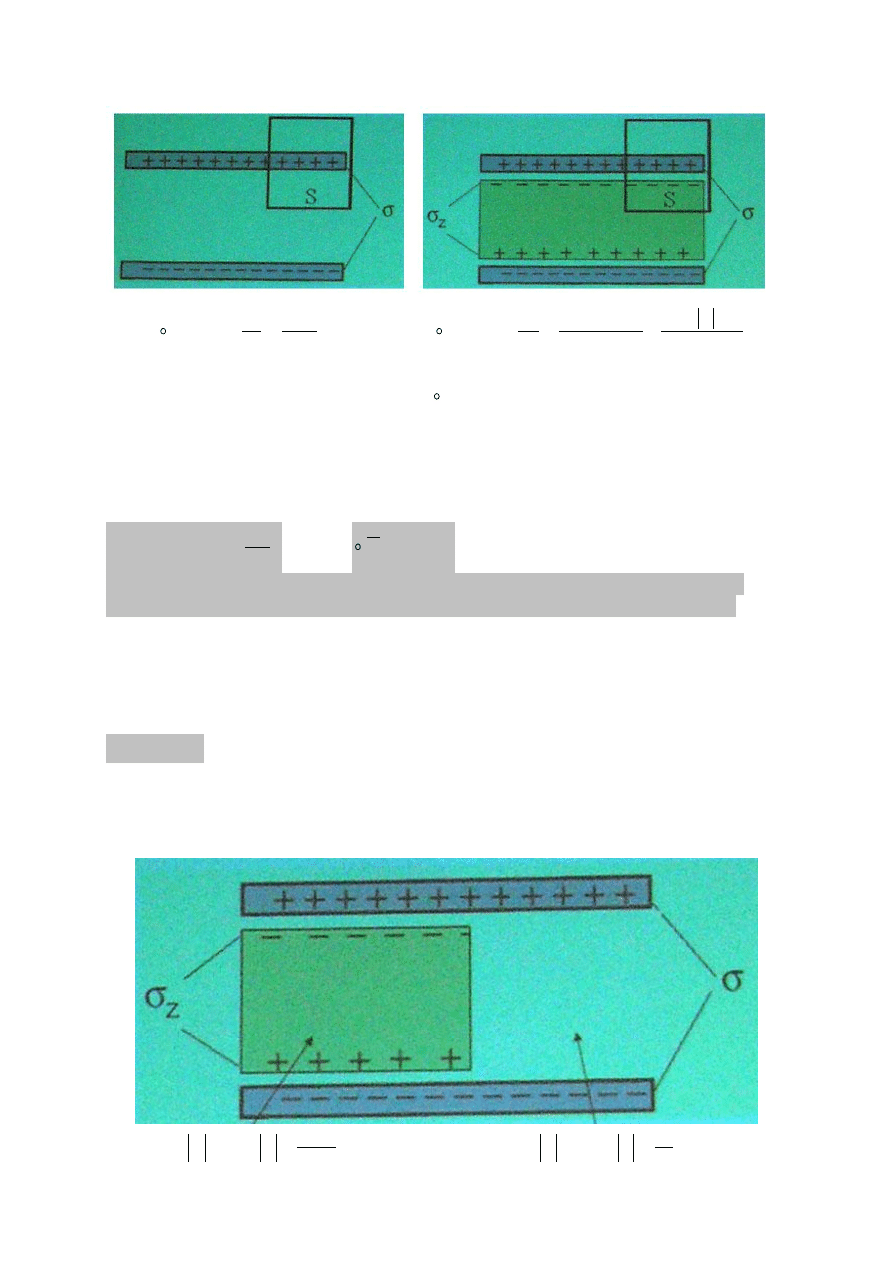
Pole elektryczne w dielektrykach
W dielektryku, nie zawierającym swobodnych ładunków elektrycznych, obserwujemy
ruch ładunków związanych polem dodatnim jonowym na odległości mikroskopowej.
W objętości dielektryka tworzą się dipole elektryczne o momencie dipolowym p
Zewnętrzne pole elektryczne indukuje moment dipolowy p związany z rozdzieleniem
na odległości L ładunku q cząstki.
Jeżeli w dielektryku mamy N cząsteczek na jednostkę objętości to wypadkowy
moment dipolowy na jednostkę objętości jest równy:
L
q
N
p
N
P
Wektor ten nazywany jest wektorem polaryzacji.
Ponieważ cząsteczki pozostają obojętne elektrycznie średni ładunek w objętości
dielektryka pozostaje równy 0.
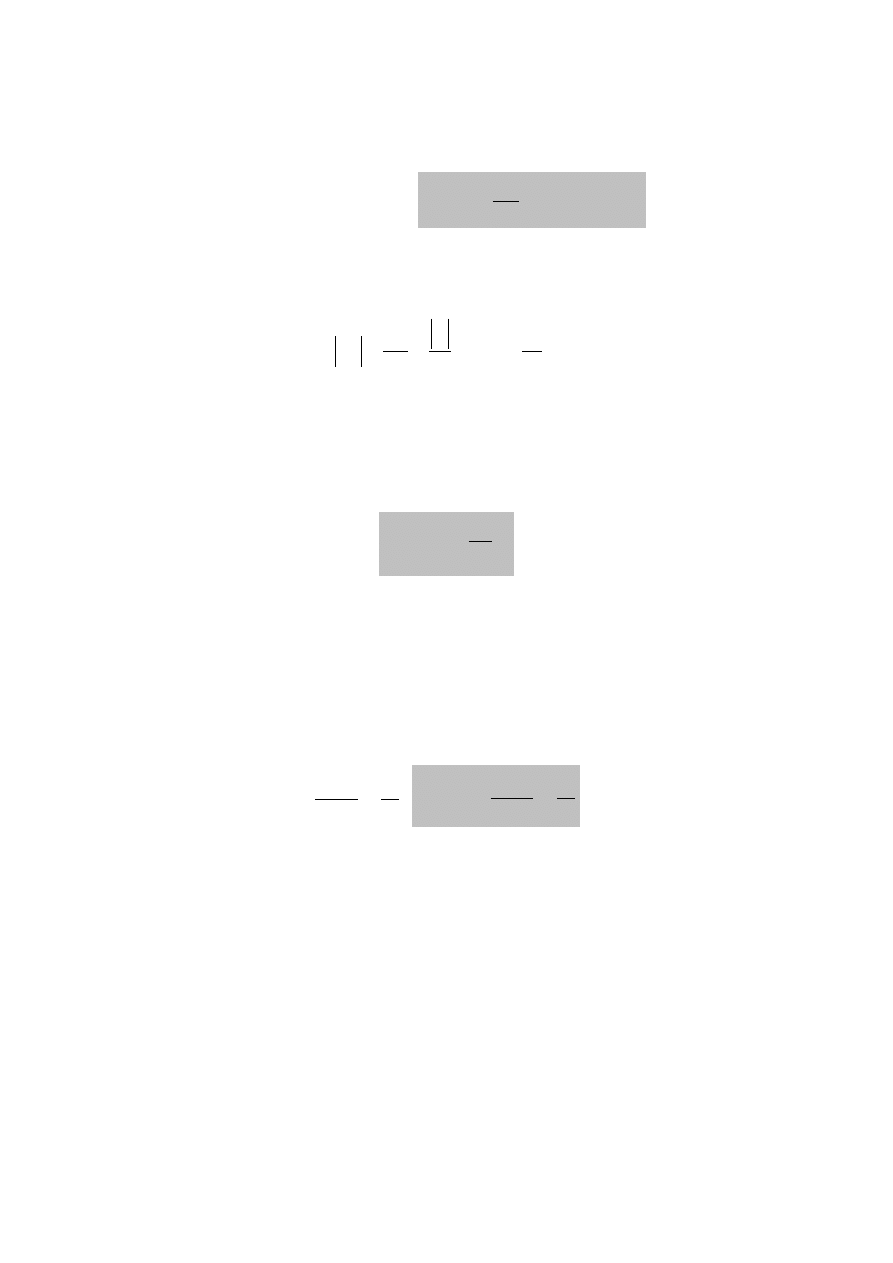
Dodatkowy ładunek Q
z
pojawi się na powierzchni zewnętrznej dielektryka. Ładunek
ten wytworzy dodatkowe pole elektryczne skierowane przeciwnie do pola
zewnętrznego.
- 21 -
Dla powierzchni S dielektryka wartość tego ładunku wynosi:
q
N
L
S
Q
z
P
L
q
N
S
Q
z
z
Ten dodatkowy ładunek powierzchniowy wytwarza w objętości dielektryka pole
wewnętrzne E
w
skierowane przeciwnie do pola zewnętrznego E
P
E
P
E
w
Z
w
0
0
0
1
Stad wypadkowe pole w dielektryku:
P
E
E
d
0
1
Zakłada się, ze moment dipolowy jednostki objętości indukowany polem E jest do
tego pola proporcjonalny
d
E
P
0
Stała
nosi nazwę podatności elektrycznej dielektryka. Podstawiając:
E
E
E
E
E
E
d
d
d
1
E
E
E
d
1
Przenikalność dielektryczna
>1 mówi nam ile razy pole w dielektryku jest mniejsze
od pola zewnętrznego.
Prawo Gaussa w dielektrykach
Obliczymy pole elektrostatyczne wytworzone prze z dwie płyty naładowane
ładunkami
i
Bez dielektryka Z dielektrykiem
- 22 -
0
0
S
Q
dS
E
v
0
0
0
'
)
(
)
(
S
P
S
Q
dS
E
z
v
Q
S
dS
P
E
v
)
(
0
Wprowadzamy wielkość wektorową – wektor indukcji elektrycznej:
2
0
m
C
P
E
D
Q
S
d
D
v
Strumień wektora indukcji elektrycznej przez powierzchnie zamknięta równy jest
ładunkowi swobodnemu zawartemu w obszarze ograniczonym ta powierzchnia.
Dla najprostszego modelu polaryzacji dielektryka:
E
E
E
D
E
P
0
0
0
0
)
1
(
E
D
0
Wektor indukcji elektrycznej
D
0
E
D
0
E
- 23 -
)
1
1
(
P
0
P
Pojemność elektryczna
Kondensator stanowią dwa przewodniki (okładki) na których może się gromadzić
ładunek elektryczny, jeżeli do okładek przyłożona będzie różnica potencjałów
Pojemność C zdefiniowana jest jako stosunek nagromadzonego ładunku Q do różnicy
potencjałów
V
C
F
V
Q
C
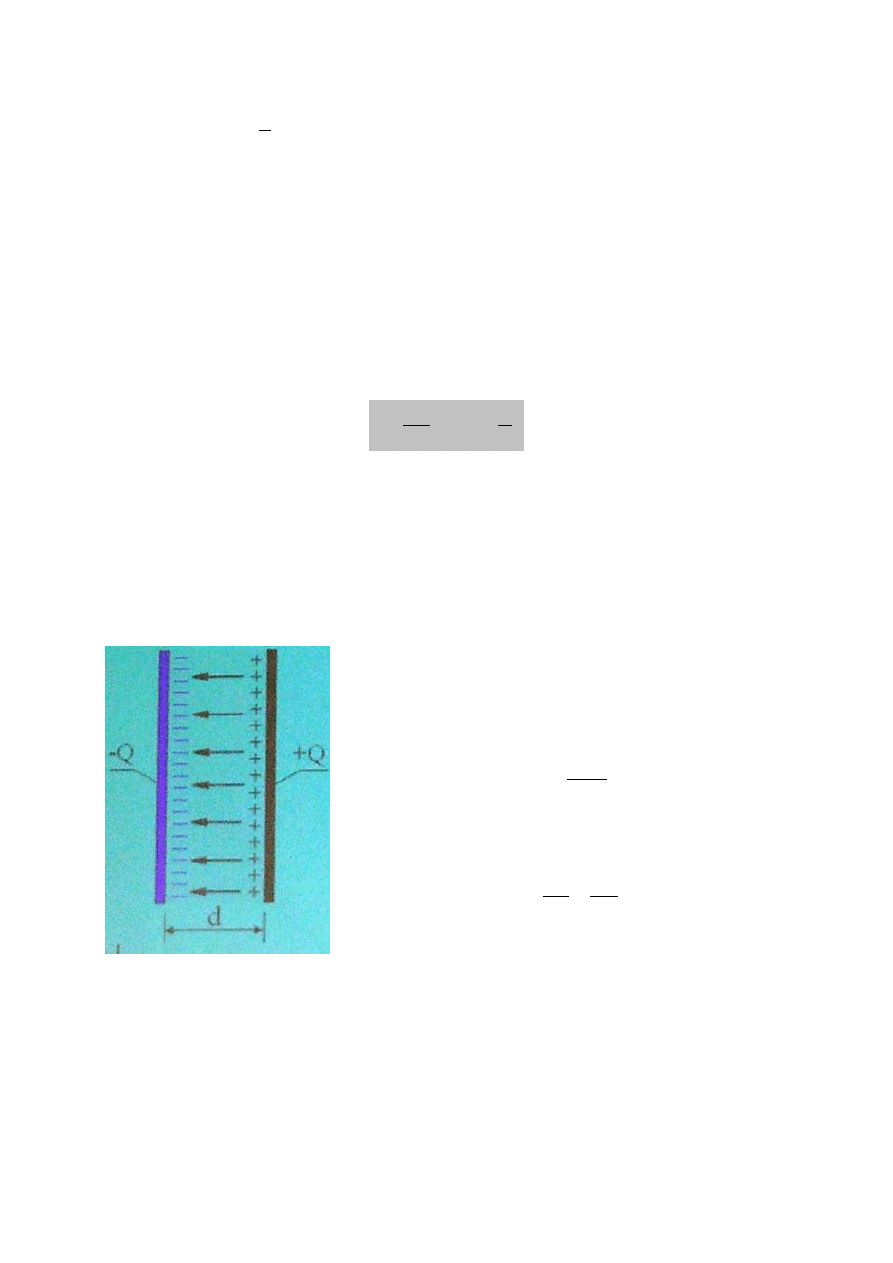
Kondensator płaski:
Różnica potencjałów pomiędzy płytami o
powierzchniach S, odległych o d i naładowanych
ładunkami Q wynosi:
S
d
Q
V
0
Stąd pojemność kondensatora:
d
V
Q
C
S
0
Pojemność
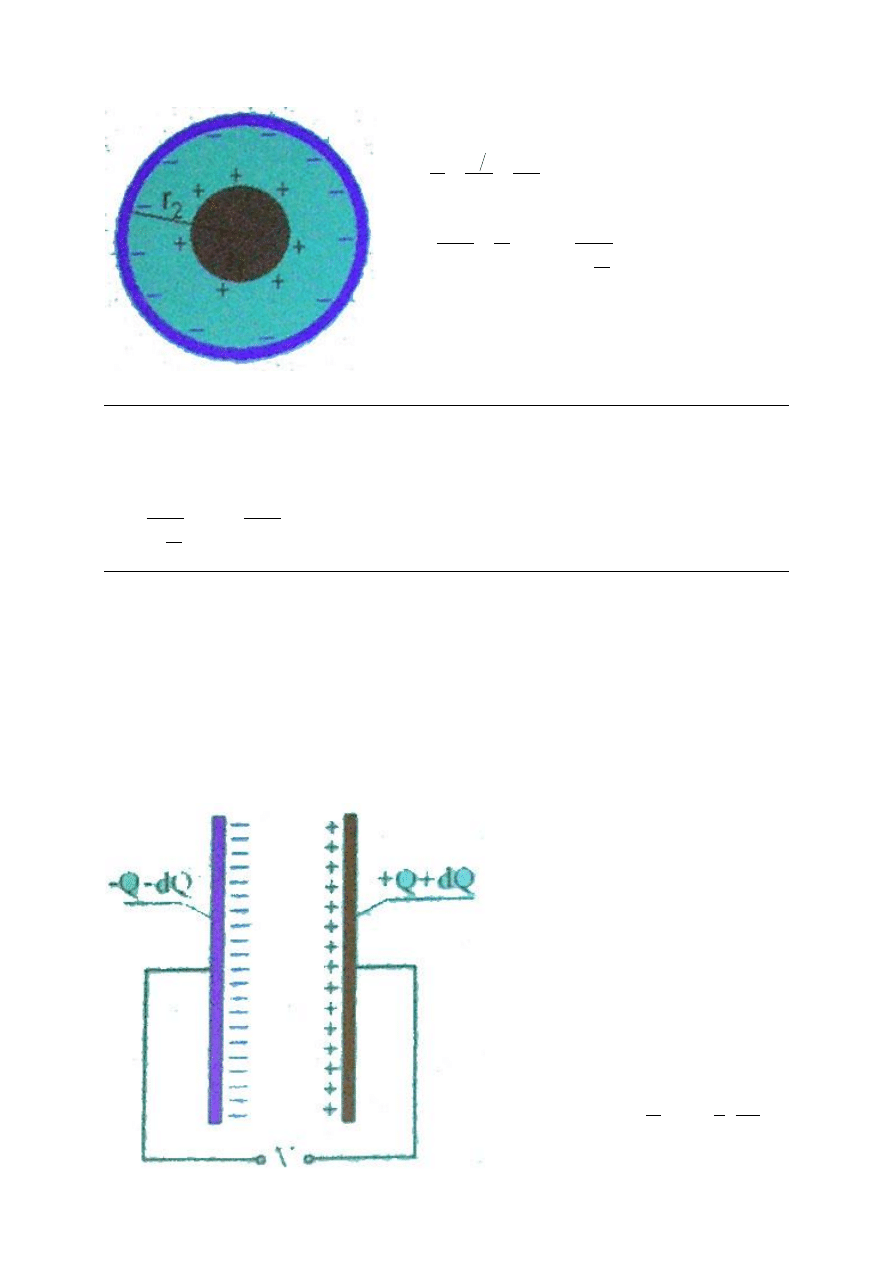
Obliczamy pojemność na jednostkę długości omawianego wcześniej kabla
koncentrycznego
- 24 -
Pojemność na jednostkę długości:
V
V
l
Q
l
C
C
l
2
2
0
2
2
0
ln
2
ln
2
r
r
C
r
r
V
l
Przykład
Ile wynosi pojemność kabla hi-fi długości 1m, w którym wewnętrzny
przewodnik na średnicę 1mm a osłona średnice 5mm
]
[
5
.
34
]
[
10
5
.
34
]
[
5
ln
2
]
[
1
ln
2
12
0
2
2
0
pF
F
m
l
m
r
r
C
l
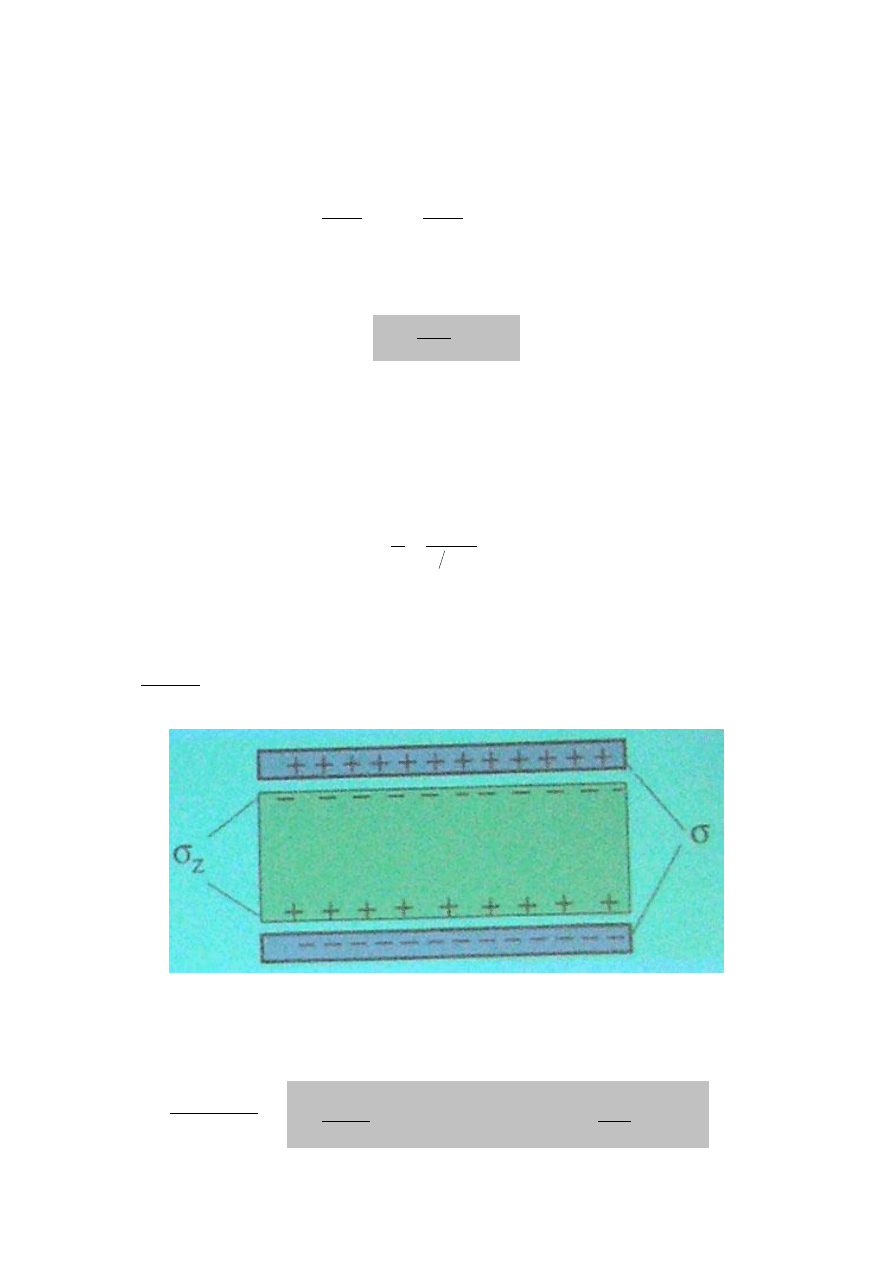
Energia pola elektrycznego w kondensatorze
W kondensatorze gromadzona jest energia pola elektrycznego.
W skutek stopniowego zwiększania różnicy potencjałów na kondensatorze od
wartości 0 do
0
V wzrasta jego ładunek od 0 do
0
Q .
Praca zużytą na przeniesienie
ładunku dQ z ujemnej okładki na
dodatnią, zwiększająca do dU
energię zgromadzona w
kondensatorze, równa jest:
dQ
V
dU
Całkowita energia zgromadzona w
kondensatorze:
0
0
0
2
0
0
2
1
Q
Q
C
Q
dQ
C
Q
dQ
V
U
- 25 -
Energie pola elektrycznego wygodniej jest wyrazić za pomocą natężenia pola:
S
Q
E
0
0
d
S
E
U
d
S
C
2
0
0
Stąd gęstość energii pola
E
:
2
0
E
d
S
U
E
Dielektryk w kondensatorze
Dielektryk wprowadzony pomiędzy okładki kondensatora zmniejsza
razy wartość
natężenia pola elektrycznego pomiędzy okładkami i zmienia jego pojemność
0
C
d
E
Q
V
Q
C
Dla kondensatora płaskiego
d
S
C
0
Obecność ośrodka dielektrycznego wpływa również na gęstość energii pola
zgromadzoną w kondensatorze
S
Q
E
0
0
2
0
2
0
0
E
d
S
U
d
S
E
U
d
S
C
E

- 26 -
Wyszukiwarka
Podobne podstrony:
,Elektrycznosc i magnetyzm, pol Nieznany
,Elektrycznosc i magnetyzm, prz Nieznany (2)
,Elektrycznosc i magnetyzm, ene Nieznany
ETwP TEST ODP WYJAS Final, ZASTOSOWANIE SILNYCH PÓL ELEKTRYCZNYCH I MAGNETYCZNYCH
mielenie elektroniki weee rohs Nieznany
Elektromonter sieci trakcyjnej Nieznany
Echo elektroniczne id 149974 Nieznany
4 Elektryczność i magnetyzm
Fizyka Prad elektryczny test id Nieznany
11 elektryczne zrodla swiatlaid Nieznany
03 wyklad elektryczny nid 4625 Nieznany
33 Schemat elektryczny FM445 id Nieznany (2)
Ludwig von Mises Ekonomia i Pol Nieznany
Mikroskopia elektronowa id 3018 Nieznany
iii2 transformacja lorentza pol Nieznany
16 Wytwarzanie podstawowych pol Nieznany (2)
Ewolucja definiowania MSp w Pol Nieznany
Elektromonter linii napowietrzn Nieznany
elektro 3 id 157863 Nieznany
więcej podobnych podstron