Akademia Techniczno-Humanistyczna
w Bielsku - Białej
Wydział Nauk o Materiałach i Środowisku
Kierunek: Budownictwo
I rok, II semestr

Ćwiczenie nr 61

„Wyznaczanie natężenia pola

elektrycznego metodą sondy

płomykowej.”

Robert Sikorski

G5/2011/BD58

Budownictwo

(niestacjonarne)

I.

CZĘŚĆ TEORETYCZNA

1) Pole elektryczne

Ładunki działają na siebie wzajemnie. Wynika stąd, że wokół każdego ładunku

występuje obszar, w którym działają siły elektrostatyczne. Obszar ten nazywamy polem

elektrycznym.

Pole elektryczne stałe w czasie nazywamy polem elektrostatycznym. Podobnie, jak w polu
grawitacyjnym, tak i tu pole obrazują linie pola, czyli linie, do których wektor natężenia pola
w każdym punkcie jest styczny.
wielkości charakteryzujące pole elektryczne to: natężenie i potencjał tego pola.

Natężeniem pola elektrycznego E nazywamy stosunek siły F, jaką pole działa na ładunek
próbny q

0

umieszczony w danym jego punkcie do wartości tego ładunku:

0

3

q

F

s

A

kg

m

C

N

E



















q

0

– to ładunek próbny, czyli jest to ładunek dodatni o bardzo małym punktowym (w

przypadku pola elektrostatycznego nieruchomym) umieszczonym w danym punkcie pola

elektrycznego.

F – to siła działająca w polu na ten ładunek

Pole elektrostatyczne w danym punkcie przestrzeni można scharakteryzować podając jego
potencjał elektryczny. Potencjał elektryczny V w danym punkcie pola jest to stosunek
energii potencjalnej E

p

ładunku próbnego dodatniego q

0

umieszczonego w tym punkcie do

wartości tego ładunku:























V

s

A

m

kg

C

J

V

q

E

V

p

3

2

0

Różnice potencjałów



V miedzy dwoma punktami pola elektrycznego okreslamy jako

napiecie elektryczne U:

[V]

V2)

-

(V1

=

V

=

U



Związek pomiędzy wartością natężenia pola E i potencjałem, V

















m

V

l

V

E

Powyższa zależność określa wartość natężenia pola elektrostatycznego jako stosunek spadku
potencjału -



V na niewielkim odcinku prostopadłym do powierzchni ekwipotencjalnej

(powierzchnia równego potencjału) do długości



l tego odcinka. Znak „ – ” wynika stąd, że

zwrot wektora E jest przeciwny do spadku potencjału.

Gęstość powierzchniową ładunku określamy jako:















2

m

C

S

q



gdzie:

q



- to ładunek elektryczny znajdujący się w elementarnej powierzchni

S



Związek między gęstością powierzchniową ładunku i natężeniem pola elektrycznego.

Ważny jest związek między gęstością powierzchniową ładunku i natężeniem pola

elektrycznego, który można zastosować np. do obliczenia wartości na podstawie
znajomości natężenia pola elektrycznego E.
Rozważmy dwie przewodzące płytki, o jednakowych rozmiarach (powierzchnia każdej
z płytek wynosi S) ustawione w odległości d od siebie. Przypuśćmy, że na jednej
płytce znajduje się ładunek Q a na drugiej – Q, a odpowiednie wartości potencjałów
oznaczymy przesz V

1

i V

2

. Zakładając pole jednorodne w całym obszarze między płytkami,

odpowiednia gęstość ładunku na wewnętrznej powierzchni jednej z płytek wynosi:

E

d

V

V

0

2

1

0

)

(





















2

m

C

gdzie:

12

0

10

85

,

8









[F/m] – przenikalność elektryczna próżni.

Sonda płomykowa - to bardzo cienką rurką przez którą przepływa gaz świetlny. Jest ona
umieszczona między okładkami kondensatora płaskiego, jej koniec znajduje się na osi
symetrii płytek. Sonda umieszczona jest na izolowanym statywie który można przesuwać
wzdłuż osi kondensatora. Odległość płytek kondensatora można zmieniać. Potencjał
mierzymy woltomierzem elektrostatycznym. Całość podłączona jest do elektrycznego
zasilacza wysokonapięciowego.

Kondensator powietrzny - składa się z dwóch równoległych płytek, na których
zgromadzone są ładunki elektryczne. Pomiędzy płytkami kondensatora powietrznego
wytworzone jest jednorodne pole elektryczne w którym linie sił pola są równoległe.

II. PRZEBIEG ĆWICZENIA

Po przygotowaniu układu przystąpiliśmy do wykonania ćwiczenia zgodnie z instrukcją tzn.

1. Sprawdzamy czy zasilacz jest wyłączony
2. Zapalamy sondę płomykową i ustawiamy jak najmniejszy płomień
3. Włączmy zasilacz i woltomierz
4. Ustawiamy sondę w takim położeniu aby woltomierz wskazywał 600V
5. Wykonujemy pomiar potencjału przez przesuwanie sondy co 2 mm dla d=40 mm i co

3 mm dla d=80mm oraz d=120mm

dla różnych odległości d między okładkami kondensatora wielokrotnie dokonaliśmy pomiaru
potencjału, wyniki są zamieszczone w tabeli nr 1:

Tabela 1.

Gdzie:

U – potencjał

l – wartość określająca położenie sondy względem okładek kondensatora

d - odległość między płytkami kondensatora

d=40[mm]

d=80[mm]

d=120[mm]

l

l

[mm]

10

21

36

V

l

[V]

V

l

[V]

V

l

[V]

1.

740

650

660

2.

880

700

700

3.

1070

800

770

4.

1230

920

840

5.

1420

1020

890

6.

1580

1150

960

7.

1780

1260

1030

8.

1960

1380

1100

9.

2120

1520

1180

10.

2330

1640

1260

11.

2490

1780

1330

12.

2660

1920

1420

13.

2840

2040

1500

14.

2960

2200

1600

15.

2340

1700

16.

2490

1780

17.

2630

1910

18.

2780

1960

19.

2920

2060

20.

2170

21.

2300

22.

2400

23.

2530

24.

2620

25.

2760

26.

2870

27.

2980

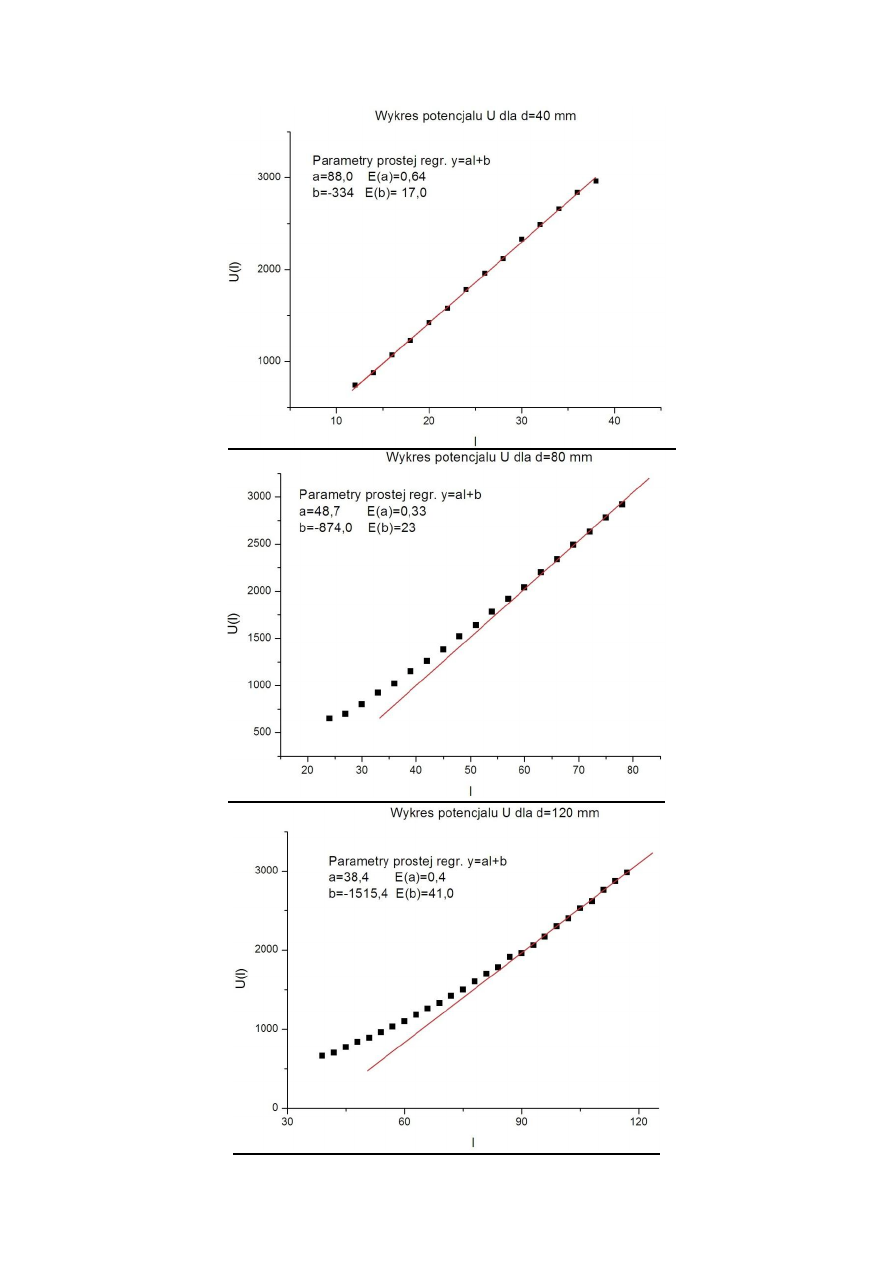
III. OPRACOWANIE WYNIKÓW.

1) W programie komputerowym obliczamy wartości współczynników a, b, funkcji liniowej oraz

błędów



a,



b. Wyniki w poniższej tabeli:

2) Obliczamy teoretyczne wartości natężenia pola elektrycznego E

t

dla poszczególnych

wartości d i zadanego napięcia miedzy okładkami (wartość napięcia odczytana z
zasilacza WN wynosi U = 3kV = 3000V)

.

E

t

=U / d [V/mm]

d - odległość między płytkami kondensatora

dla d = 40 mm

5

7

40

3000

E

t





V/mm

dla d = 80 mm

5

,

37

80

3000

E

t





V/mm

dla d = 120

25

120

3000

E

t





V/mm

3) Ze współczynnika a prostej regresji wyznaczamy natężenie pola elektrycznego E

d

, gdyż

wartości a są równe wartościom E

d

:

dla d = 40 mm

E

d

= 88,0 V/mm

dla d = 80

E

d

= 49,0 V/mm

dla d = 120 mm

E

d

= 38,4 mm

4) Obliczamy względne odchylenia



(wyrażone w procentach) wartości doświadczalnych

natężenia pola elektrycznego E

d

od wartości teoretycznych E

t

ze wzoru:

%

100

E

E

-

E

=

t

t

d





dla d

1

= 40 mm

%

3

,

17

%

100

75

75

88

=









dla d

2

= 80 mm

%

31

%

100

37,5

5

,

37

49

=









dla d

3

= 120 mm

%

54

%

100

25

25

4

,

38











Wyniki obliczeń zestawiamy w poniższej tabelce:

d=40[mm]

d=80[mm]

d=120[mm]

a = 88 V/mm



a = 0,65 V/mm a= 49



a=0,33

a=38,4



a=0,4

b = -334 V/mm



b = 17,0

b= -837



b=23

b= -1516



b=41

d

l

=40 mm

d

2

=80 mm

d

3

=120 mm

E

d

[V/mm]

E

t

[V/mm]



[%]

E

d

[V/mm]

E

t

[V/mm]



[%]

E

d

[V/mm]

E

t

[V/mm]



[%]

88

75

17,3

49

37,5

31

38,4

25

54

5) Obliczamy gęstości powierzchniowe ładunku



d

na wewnętrznej powierzchni jednej z

płytek, na podstawie trzech doświadczalnych zależności U=f(l) wyznaczonych w pkt.1.















m

F

mm

V

E

d

0





d = 40 mm
E

d

= 87,8 [V/mm]































































































2

7

2

13

2

15

3

12

12

0

10

8

,

7

10

8

,

7

10

8

,

778

10

10

85

,

8

8

,

87

10

85

,

8

88,0

mm

C

mm

C

mm

C

mm

F

mm

V

m

F

mm

V

E

d







d = 80 mm
E

d

=48,7 [V/mm]



















































2

7

2

13

12

0

10

34

,

4

10

34

,

4

10

85

,

8

49

mm

C

mm

C

m

F

mm

V

E

dl







d = 120 mm
E

dl

=38,4 [V/mm]



















































2

7

2

13

12

0

10

4

,

3

10

40

,

3

10

85

,

8

4

,

38

mm

C

mm

C

m

F

mm

V

E

dl







Wyniki obliczeń zestawiamy w poniższej tabelce:

6) Dla wszystkich 3 przypadków liczymy liczbę elektronów przypadającą na 1 mm

2

powierzchni płytki. Otrzymuje się ją przez podzielenie obliczonych wartości



przez

ładunek elementarny e = 1,602·10

-19

C = 1,602·10

-13



C

Dla d=40mm

liczba elektronów







































2

6

2

13

7

1

10

0

,

5

10

602

,

1

10

8

,

7

mm

C

mm

C

e







Dla d=80mm

liczba elektronów







































2

6

2

13

7

1

10

7

,

2

10

602

,

1

10

34

,

4

mm

C

mm

C

e







Dla d=120mm

liczba elektronów







































2

6

2

13

7

1

10

1

,

2

10

602

,

1

10

4

,

3

mm

C

mm

C

e







d

1

=40mm

d

2

=80mm

d

3

=120mm

E

d

[V/mm]

σ

x 10

-7

[μC/mm

2

]

E

d

[V/mm]

σ

x 10

-7

[μC/mm

2

]

E

d

[V/mm]

σ

x 10

-7

[μC/mm

2

]

88

7,8

49

4,34

38,4

3,4

d=40mm

d=80mm

d=120mm

liczba elektronów

[1/mm

2

]

liczba elektronów

[1/mm

2

]

liczba elektronów

[1/mm

2

]

5,0*10

6

2,7*10

6

2,1*10

6

IV. WNIOSKI.

Wyniki różnią się od wielkości tablicowych z powodu niedokładności podziałki

określającej odległość sondy od lewej okładki kondensatora, w ćwiczeniu używaliśmy linijki
do zmierzenia odległości między okładkami. Błędy pojawiły się przy odczytywaniu wyników
z woltomierza (drgania wskazówki spowodowane wstrząsami stołu).