Michał Szuchnik

Elektrotechnika

Sem. V

Niestacjonarne

15-12-2012r.

Zbadać własności dynamiczne układu nieliniowego pokazanego na rysunku:

Przekaźnik dwupołożeniowy bez histerezy B=5. Transmitancja:

10

5

Obliczam transmitancję widmową G(jω):

10

5

Korzystam z kryterium Nyquista dla układów nieliniowych:

0

Wydzielamy z powyższego wyrażenia część rzeczywistą i część urojoną:

0

0

Zatem:

L(jω)=10

Re[L(jω)]=10

Im[L(jω)]=0

M(jω)=jω(jω+5)

2

=(jω)[(jω)

2

+2(jω)×5+5

2

]=(jω)[-ω

2

+10jω+25]=-jω

3

-10ω

2

+j25ω

Re[M(jω)]=-10ω

2

Im[M(jω)]=-ω

3

+25ω

Y

X

B

-B

J(A)

G(s)

X(t)

Y(s)

+

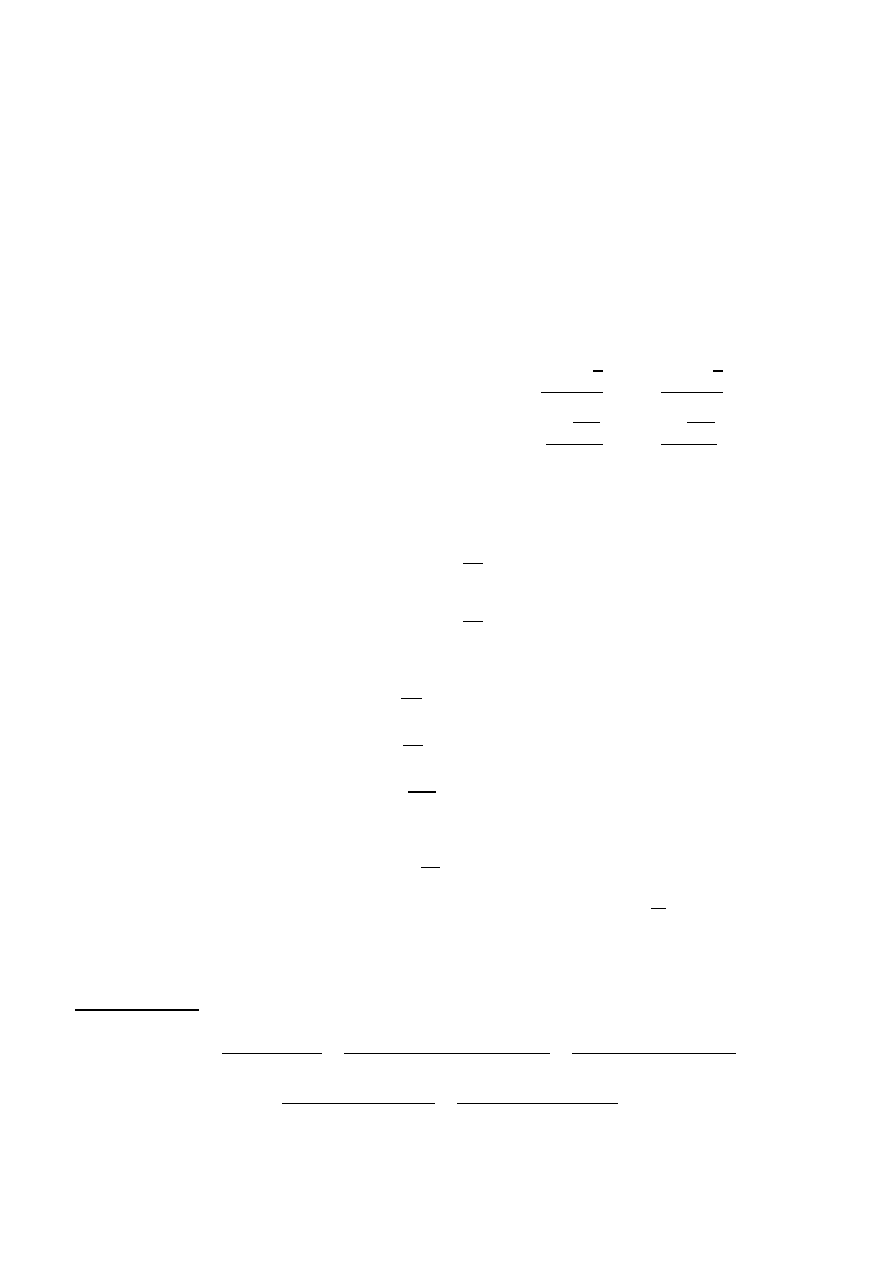
Czyli:

10 10

0

0 ·

25 0

Z równania drugiego obliczamy pulsację ω:

25 0

25 0

ω=0 v -ω

2

+25=0

Δ=b

2

-4ac

Δ=-4×(-1)×25

Δ=100

√∆

2!

;

√∆

2!

√100

2 · 1 ;

√100

2 · 1

#

0; $

5; $

5

Równanie zatem ma trzy rozwiązania w dziedzinie liczb rzeczywistych. Dwa skrajne rozwiązania odrzucamy.
Obliczamy teraz amplitudę A. Funkcja opisująca przekaźnik dwupołożeniowy bez histerezy dana jest wzorem:

4&

'

Ponieważ B=5, zatem

20

'

czyli:

10 ·

20

' 10 ·

0

10 ·

20

' 10 · 5

0

200

' 250

200 250'

1

4'

Dla pulsacji ω=5 w układzie nieliniowym powstaną drgania okresowe o amplitudzie A=

#

()

Metoda graficzna:
Wyznaczamy transmitancję widmową:

10

5

10

jωjω

2 · jω · 5 5

10

jωω

j10ω 25

10

10

25

10

10

25

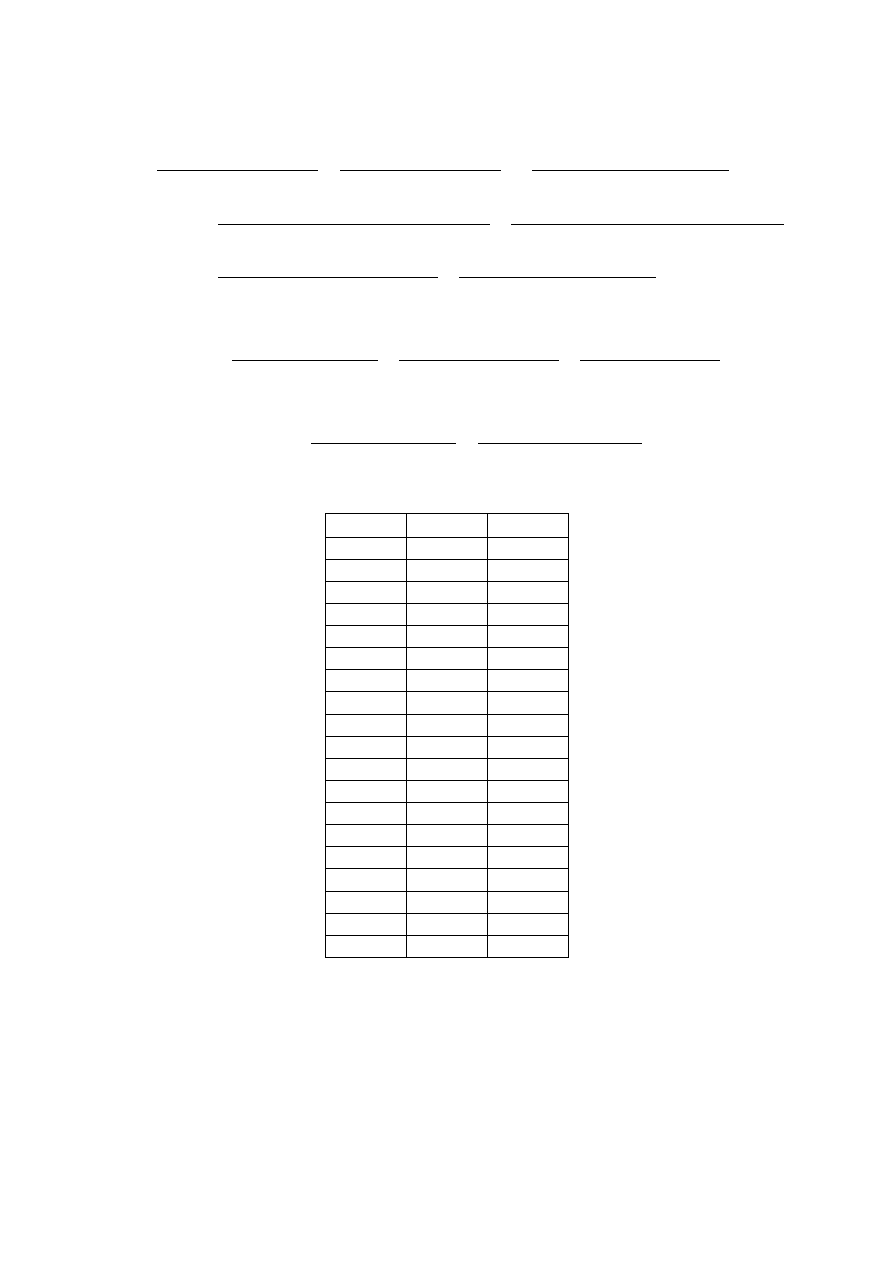
Aby rozdzielić część rzeczywistą i część urojoną powyższej liczby zespolonej należy licznik i mianownik
pomnożyć przez liczbę sprzężoną.

10

10

25 · +

10

25

10

25,

100

10

250

10

25

100

10

250

100

(

-

2 ·

· 25 625

100

10

250

100

(

-

2 ·

· 25 625

100

10

250

100

(

-

50

(

625

100

10

250

50

(

-

625

Zatem część rzeczywista P(ω) wynosi:

/

100

50

(

-

625

100

50

(

625

100

50

(

625

Część urojona Q(ω) wynosi:

0

10

250

50

(

-

625

10

250

50

1

625

Aby narysować charakterystykę amplitudowo-fazową należy podstawić do powyższych wzorów ω w szerokim
zakresie zmian od wartości 0 do ∞

ω

P(ω)

Q(ω)

1

-0,14793

-0,35503

2

-0,11891

-0,12485

3

-0,08651

-0,04614

4

-0,05949

-0,01338

5

-0,04

0

6

-0,02687 0,004927

7

-0,01826 0,006261

8

-0,01262 0,006155

9

-0,0089 0,005538

10

-0,0064

0,0048

11

-0,00469 0,004094

12

-0,0035 0,003472

13

-0,00266 0,002943

14

-0,00205 0,002501

15

-0,0016 0,002133

20

-0,00055 0,001038

30

-0,00012 0,000341

40

-3,8E-05 0,000149

50

-1,6E-05

7,76E-05

Kształt charakterystyki G(jω) przedstawia rysunek:

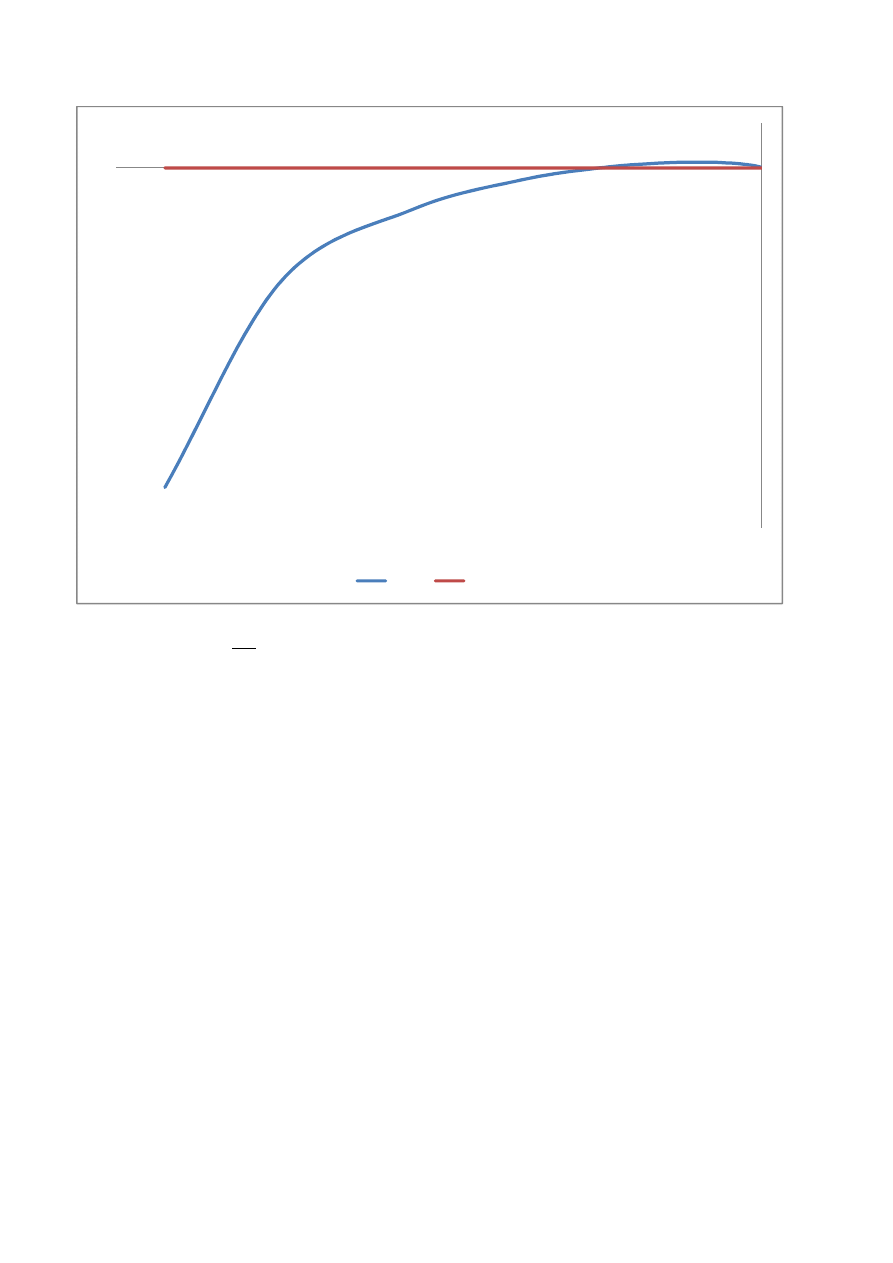
Ponieważ charakterystyka amplitudowo fazowa G(jω) części liniowej do punktu P nie obejmuje wykresu

krytycznego

2

#

34

, zatem układ jest stabilny. W punkcie P następuje przecięcie obu wykresów, zatem

powstają drgania okresowe nietłumione o amplitudzie A i pulsacji ω wyznaczonej w rozwiązaniu analitycznym i
układ nieliniowy wejdzie w tryb pracy niestabilnej.

-0,4

-0,35

-0,3

-0,25

-0,2

-0,15

-0,1

-0,05

0

0,05

-0,16

-0,14

-0,12

-0,1

-0,08

-0,06

-0,04

-0,02

0

Im

Re

G(jω)

-1/J(A)

P