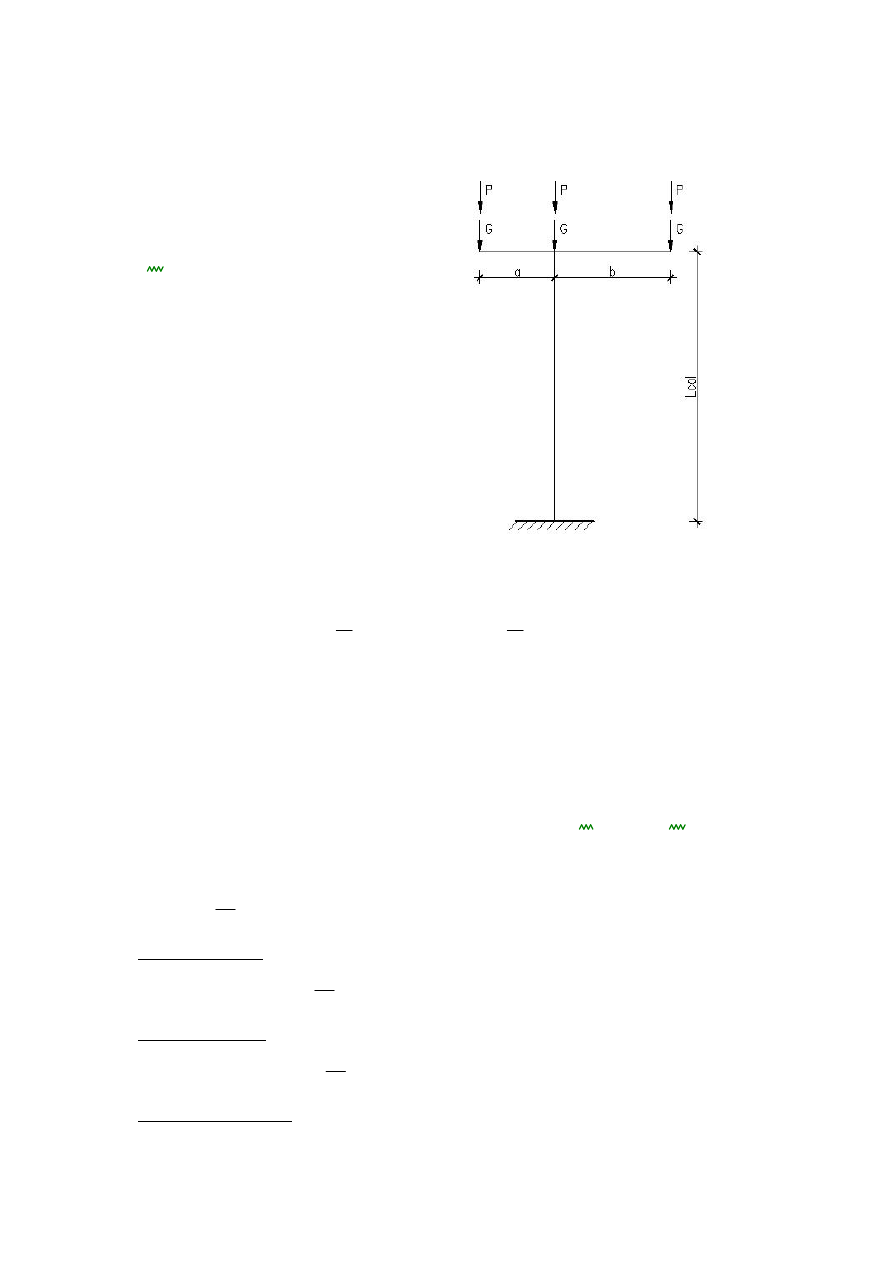
1. Dane geometryczne i założenia wyjściowe do projektowania:
Lcol
6.8m
:=
- wysokość słupa
a
2.3m
:=
- wysięg lewego rygla
b
3.3m
:=
- wysięg prawego rygla
G
55kN
:=
- ciężar rurociagu
P
110kN
:=
- ciężar m edia
f
0.12
:=
- współczynnik tarcia
Lokalizacja: Wrocław
głębokość strefy przemarzania:
hz
1.0m
:=
2. Dobór wymiarów poszczgólnych elementów:
2.1 Słup
l0
2 Lcol
13.6 m
=
:=
hs1
l0
20
0.68 m
=
:=
hs2
l0
25
0.544 m
=
:=
przyjmuje:
hs
0.6m
:=
bs
hs 0.6 m
=
:=
2.2 Rygiel:
br
bs 0.6 m
=
:=
hr
br 0.2m
+
0.8 m
=
:=
2.3 Stopa fundamentowa
Wstępnie przyjęto wymiary stopy fundam entowej:
B
4.0m
:=
L
4.0m
:=
H
1.1m
:=
3. Zestawienie obciążeń
3.1. Obciążenia stałe
γbet
25
kN
m
3
:=
- ciężar obj. betonu
γG
1.35
:=
1.0
(
) - wsp. obliczeniowy
Ciężar własny rygla
gr
hr br
γbet
γG
16.2
kN
m
=
:=
Ciężar własny słupa
gs
hs bs
γbet
γG
12.15
kN
m
=
:=
Ciężar własny rurociągu

Gd
G
γG
74.25 m
kN
m
=
:=
3.2. Obciążenia zmienne
γQ
1.50
:=
0.0
(
) - wsp. obliczeniowy dla obciążenia zmiennego
Obciążenie pionowe
Pd
P
γQ
165 kN
=
:=
- obciążenia pionowe od m edium
Obciążenie poziome
Hd
f Pd Gd
+
(
)
28.71 kN
=
:=
- obciążenia pozoime od tarcia m edium o ścianki rurociągu
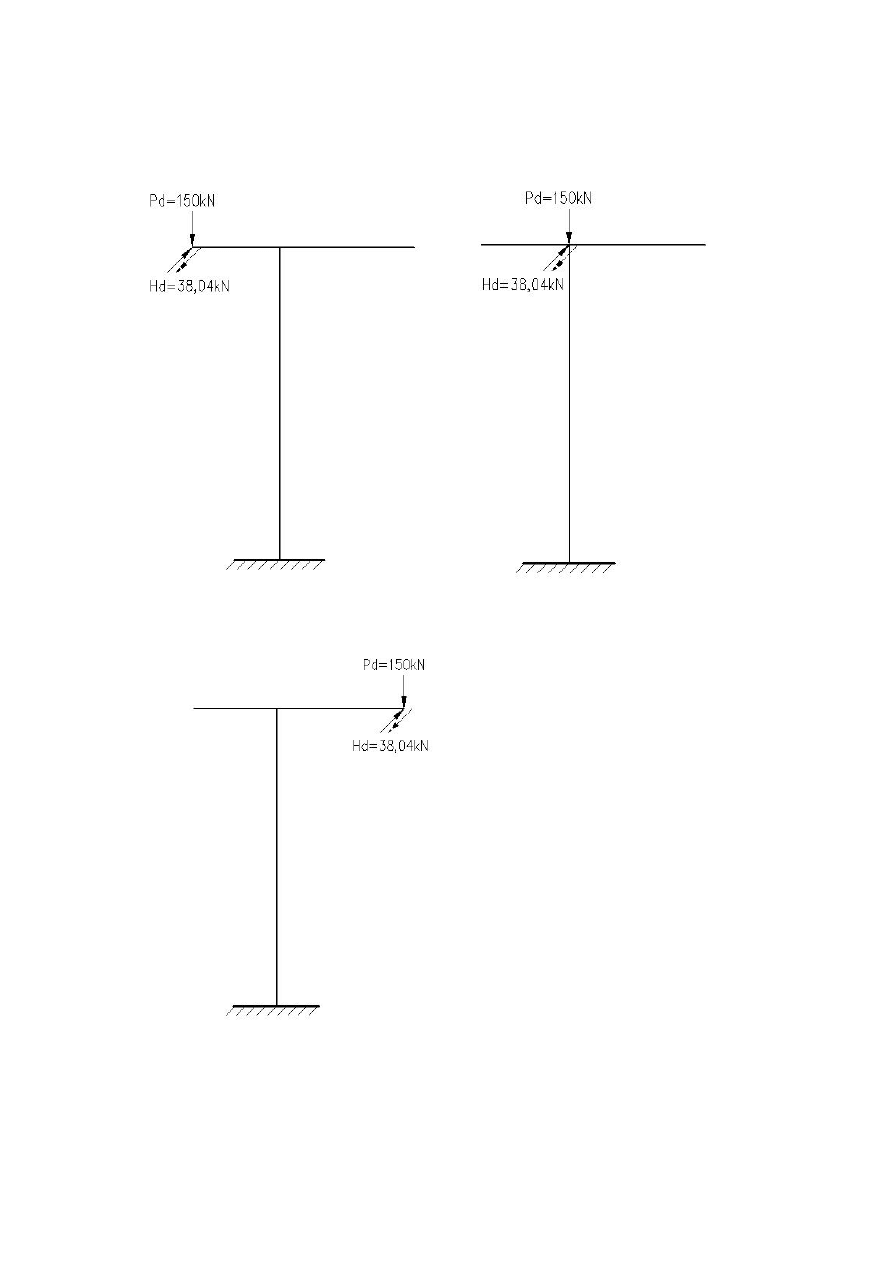
4.3 Obciążenia zmienne w pkt A
4.4 Obciążenia zmienne w pkt. B
4.5 Obciążenia zmienne w pkt. C

5. Zestwienie maksymalnych sił przekrojowych
5.1 Rygiel lewy
Mx.rl
gr a
2
2
Gd a
+
Pd a
+
593.124 kN m
=
:=
My.rl
Hd a
66.033 kN m
=
:=
Qx.rl
gr a
Gd
+
Pd
+
276.51 kN
=
:=
Qy.rl
Hd 28.71 kN
=
:=
5.2 Rygiel prawy
Mx.rp
gr b
2
2
Gd b
+
Pd b
+
877.734 kN m
=
:=
My.rp
Hd b
94.743 kN m
=
:=
Qx.rp
gr b
Gd
+
Pd
+
292.71 kN
=
:=
Qy.rp
Hd 28.71 kN
=
:=
5.3 Słup
Kombinacje dla zginania
I Kom binacja (Maxymalny moment M.x oraz wartości odpowiadajace)
Mx.s
gr
b
2
2
gr
a
2
2
-
Gd b a
-
(
)
+
Pd b
+
664.11 kN m
=
:=
My.s
Hd Lcol
195.228 kN m
=
:=
Ns
gr a b
+
(
)
gs Lcol
(
)
+
3 Gd
+
Pd
+
561.09 kN
=
:=
Qy.s
Hd 28.71 kN
=
:=
II. Kom binacja (Maxymalny m oment M.y oraz wartości odpowiadające)
My.s
3Hd Lcol
585.684 kN m
=
:=
Mx.s
gr
b
2
2
gr
a
2
2
-
Gd b a
-
(
)
+
Pd b a
-
(
)
+
284.61 kN m
=
:=
Ns
gr a b
+
(
)
gs Lcol
(
)
+
3 Gd
+
3Pd
+
891.09 kN
=
:=
Qy.s
3Hd 86.13 kN
=
:=
Kombinacje dla skręcania
I. Maksym alny m oment skręcający i odpowiadająca m u siła ścinająca:
Mz.s
a
b
+
(
) Hd
160.776 kN m
=
:=
Qy.s
Hd 28.71 kN
=
:=
II. Maksymalna siła ścinająca i odpowiadający mom ent skręcający:
Mz.s
b
a
-
(
) Hd
28.71 kN m
=
:=
Qy.s
3Hd 86.13 kN
=
:=
6. Dane materiałowe
6.1 Beton C30/37
γc
1.4
:=
współczynnik bezpieczeństwa
fck
30MPa
:=
wytrzymałość charakterystyczna na ściskanie betonu
fcd
fck
γc
21.429 MPa
=
:=
wytrzymałść obliczeniowa na śćiskanie betonu
fcm
fck 8MPa
+
38 MPa
=
:=
średnia wytrzymałośc na ściskanie betonu
fctm
0.3
fck
MPa
2
3
MPa
:=
średnia wytrzymałość na rozciąganie betonu
fctk
2MPa
:=
wytrzymałość charakterystyczna na rozciąganie betonu
fctd
fctk
γc
1.429 MPa
=
:=
wytrzymałość obliczeniowa na rozciąganie betonu
Ecm
22 0.1
fcm
MPa
0.3
MPa
10
3
32.837 GPa
=
:=
średni m oduł sprężystości betonu
6.2 Stal zbrojeniowa RB 500W
współczynnik bezpieczeństwa
γs
1.15
:=
fyk
500MPa
:=
charakterystyczna granica plastyczności
fyd
fyk
γs
434.783 MPa
=
:=
obliczeniowa granica plastyczności
ftk
550MPa
:=
wytrzymałość charakterystyczna na rozciąganie
ftd
ftk
γs
478.261 MPa
=
:=
wytrzymałość obliczeniowa na rozciąganie
Es
200GPa
:=
m oduł sprężystości stali
7. Wymiarowanie rygla
7.1 Otulenie zbrojenia
Klasa ekspozycji XC4
Zalecana klasa konstrukcji: S4
ϕ
25mm
:=
przyjęta średnica zbrojenia
cmin.b
ϕ
25 mm
=
:=
otulenie ze względu na przyczepność
cmin.dur
30mm
:=
otulenie ze wzgl. na warunki środowiska

Δcdur.γ
0mm
:=
otulenie ze wzgl. na bezpieczeństwo
Δcdur.st
0mm
:=
zm niejsznie otulenia ze wzgl. na stal nierdzewną
Δcdur.add
0mm
:=
zm niejszenie otulennia ze wzgl. na dodatkowe
zabezpieczenie
Δcdev
10mm
:=
dodatek ze wzgl. na odchyłkę
Minim alne otulenie:
cmin
max cmin.b cmin.dur Δcdur.γ
+
Δcdur.st
-
Δcdur.add
-
,
10mm
,
(
)
30 mm
=
:=
Nominalen otulenie:
cnom
cmin Δcdev
+
40 mm
=
:=
7.2 Graniczna względna wysokość strefy ściskanej
εcu2
0.0035
:=
odkształcenia w betonie ściskanym
εyd
fyd
-
Es
2.174
-
10
3
-
=
:=
odkształcenia w stali
ξeff
εcu2
εcu2 εyd
-
0.617
=
:=
względna wysokość strefy ściskanej
ξeff.lim
0.8
ξeff
0.493
=
:=
graniczna względna wysokośc strefy ściskanej
7.3 Wymiarowanie rygla na zginanie
Momenty zginające:
Mx.rl 593.124 kN m
=
Mx.rp 877.734 kN m
=
My.rl 66.033 kN m
=
My.rp 94.743 kN m
=
Obliczenie potrzebnego zbrojenia A.s1x
hr 0.8 m
=
wysokość rygla
br 0.6 m
=
szerokość rygla
dx
hr 0.5ϕ
-
8mm
-
cnom
-
0.74 m
=
:=
wysokość użyteczna
MEd.x
Mx.rp 877.734 kN m
=
:=
m oment obliczeniowy
Sc.eff
MEd.x
br dx
2
fcd
0.125
=
:=
współczynnik pom ocniczy

ξeff
1
1
2 Sc.eff
-
-
0.134
=
:=
zasięg efektywnej strefy ściskanej
ξeff.lim 0.493
=
graniczny zasięg strefy ściskanej
ξeff ξeff.lim
<
1
=
WARUN EK SP EŁNIONY
xeff
dx ξeff
9.893 cm
=
:=
efektywna wysokość strefy ściskanej
As1.x
fcd xeff
br
fyd
29.256 cm
2
=
:=
pole zbrojenia
Obliczenie powierzchni zbrojenia minimalnego:
k
0.65
:=
współczynnik zależny od naprężeń w betonie
kc
0.4
:=
współczynnik zależny od rozkładu naprężeń
Act
0.5 br
hr
0.24 m
2
=
:=
pole rozciąganego przekroju
σs.lim
200MPa
:=
przyjęte naprężenia w zbrojeniu po zerwaniu
As.min.1
0.26
fctm
fyk
br
dx
6.683 cm
2
=
:=
As.min.2
0.0013 br
dx
5.768 cm
2
=
:=
As.min.3
k kc
fctm
Act
σs.lim
9.037 cm
2
=
:=
Powierzchnia zbrojenia minimalnego:
As.min
max As.min.1 As.min.2
,
As.min.3
,
(
)
9.037 cm
2
=
:=
As1.x As.min
>
1
=
WARUN EK SP EŁNIONY
Przyjęcie zbrojenia: As1.x 29.256 cm
2
=
ϕ
22mm
:=
Przyjęto 11ϕ25
As1.x.prov
11
π ϕ
2
4
41.815 cm
2
=
:=
Obliczenie potrzebnego zbrojenia A.s1y
hr 0.8 m
=
wysokość rygla
br 0.6 m
=
szerokość rygla
dy
br 0.5ϕ
-
8mm
-
cnom
-
0.541 m
=
:=
wysokość użyteczna
MEd.y
My.rp 94.743 kN m
=
:=
m oment obliczeniowy

Sc.eff
MEd.y
hr dy
2
fcd
0.019
=
:=
współczynnik pom ocniczy
ξeff
1
1
2 Sc.eff
-
-
0.019
=
:=
zasięg efektywnej strefy ściskanej
ξeff.lim 0.493
=
graniczny zasięg strefy ściskanej
ξeff ξeff.lim
<
1
=
WARUN EK SP EŁNIONY
xeff
dy ξeff
1.031 cm
=
:=
efektywna wysokość strefy ściskanej
As1.y
fcd xeff
hr
fyd
4.067 cm
2
=
:=
pole zbrojenia
Obliczenie powierzchni zbrojenia minimalnego:
k
0.76
:=
współczynnik zależny od naprężeń w betonie
kc
0.4
:=
współczynnik zależny od rozkładu naprężeń
Act
0.5 br
hr
0.24 m
2
=
:=
pole rozciąganego przekroju
σs.lim
200MPa
:=
przyjęte naprężenia w zbrojeniu po zerwaniu
As.min.1
0.26
fctm
fyk
br
dy
4.889 cm
2
=
:=
As.min.2
0.0013 hr
dy
5.626 cm
2
=
:=
As.min.3
k kc
fctm
Act
σs.lim
10.566 cm
2
=
:=
Powierzchnia zbrojenia minimalnego:
As.min
max As.min.1 As.min.2
,
As.min.3
,
(
)
10.566 cm
2
=
:=
As1.y As.min
>
0
=
WARUN EK N IE SPEŁNIONY- przyjęcie zbrojenia minim alnego
Przyjęcie zbrojenia: As1.y
As.min 10.566 cm
2
=
:=
Przyjęto 4ϕ22
As1.y.prov
4
π ϕ
2
4
15.205 cm
2
=
:=
Nośność obliczeniowa przekroju na zginanie w płaszczyśnie x:
ξeff
fyd As1.x.prov
fcd br
dx
0.191
=
:=

ξeff ξeff.lim
<
1
=
MRd.x
fcd br
dx
2
ξeff
1
0.5
ξeff
-
(
)
1.216
10
3
kN m
=
:=
Nośność obliczeniowa przekroju na zginanie w płaszczyśnie y:
ξeff
fyd As1.y.prov
fcd hr
dy
=
:=
ξeff ξeff.lim
<
1
=
MRd.y
fcd hr
dy
2
ξeff
1
0.5
ξeff
-
(
)
344.908 kN m
=
:=
Sprawdzenie warunku nośności na zginanie dwukierunkowe:
MEd.x
MRd.x
MEd.y
MRd.y
+
0.997
=
WARUN EK SP EŁNIONY
7.4 Wymiarowanie rygla na ścinanie
Przekrojowe siły poprzeczne:
Qx.rl 276.51 kN
=
VEd.x
Qx.rp 292.71 kN
=
:=
Qy.rl 28.71 kN
=
VEd.y
Qy.rp 28.71 kN
=
:=
Wymiarowanie na ścinanie w płaszczyżnie x:
Sprawdzenie czy waymagane jest wym iarowanie zbrojenia na ścinanie
k
min 1
200mm
dx
+
2
,
1.52
=
:=
CRd.c
0.18
γc
0.129
=
:=
współczynniki
νmin
0.035 k
3
2
fck
MPa
0.5
MPa
0.359 MPa
=
:=
Asl
As1.x.prov 41.815 cm
2
=
:=
pole zastosowanego zbrojenia na
zginanie
ρL
min 0.02
Asl
br dx
,
9.424
10
3
-
=
:=
stopień zbrojenia przekroju
obliczeniowa nosność na ścinanie
elementów bez zbrojenia
VRd.c
CRd.c k
100
ρL
fck
MPa
1
3
br
dx
MPa
264.167 kN
=
:=
VRd.c.min
νmin br
dx
159.406 kN
=
:=
VRd.c VEd.x
>
0
=
WARUN EK N IE SPEŁNIONY- wymagane wym iarowanie zbrojenia na
ścinanie
Sprawdzenie warunku ściskanych krzyżulców betonowych
fywd
fyd 434.783 MPa
=
:=
obliczeniowa granica plastyczności
dx 0.74 m
=
wysokość użyteczna przekroju
br 0.6 m
=
szerokość rygla
ramię sił wewnetrznych
z
0.9 dx
66.555 cm
=
:=
współczynnik zależny od naprężenia
w pasie ściskanym (kst. niesprężone)
αcw
1
:=
ν
0.6 1
fck
250MPa
-
0.528
=
:=
współczynnik redukcji wytrzym ałości
betonu zarysowanego przy ścinaniu
Θ
26.6deg
:=
cot
Θ
( )
1.997
=
kąt nachylenia krzyżólców bet.
m ax. siła ścinąjąca jaką przenoszą
krzyzólce betonowe
VRd.max
αcw br
z
ν
fcd
cot
Θ
( )
tan
Θ
( )
+
1.809
10
3
kN
=
:=
VRd.max VEd.x
>
1
=
WARUN EK SP EŁNIONY - krzyżulce betonowe nie ulegną zmiażdżeniu
Wyznaczenie rozstawu zbrojenia poprzeznego:
α
90deg
:=
kąt nachylenia strzemion
ϕs
8mm
:=
średnica strzem ion
pole przekroju zbrojenia na ścianie
(strzem iona 2-cięte)
Asw
2
π
ϕs
2
2
1.005 cm
2
=
:=
s1
Asw
VEd.x
fywd
z
cot
Θ
( )
19.846 cm
=
:=
Dobrano: s1
15cm
:=
Sprawdzenie rozstawu i stopnia zbrojenia:
sI.max
0.75dx 55.463 cm
=
:=
m aksym alny rozstaw strzemion
s1 sI.max
<
1
=
WARUN EK SP EŁNIONY
ρw.min
0.08
fck MPa
1
-
fyk MPa
1
-
0.088 %
=
:=
m inimalny stopień zbrojenia
ρw
Asw
br s1
0.112 %
=
:=
stopień zbrojenia
ρw ρw.min
>
1
=
WARUN EK SP EŁNIONY
Wymiarowanie na ścinanie w płaszczyżnie y:
Sprawdzenie czy waymagane jest wym iarowanie zbrojenia na ścinanie
k
min 1
200mm
dy
+
2
,
1.608
=
:=
CRd.c
0.18
γc
0.129
=
:=

współczynniki
νmin
0.035 k
3
2
fck
MPa
0.5
MPa
0.391 MPa
=
:=
Asl
As1.y.prov 15.205 cm
2
=
:=
pole zastosowanego zbrojenia na
zginanie
ρL
min 0.02
Asl
br dx
,
0.343 %
=
:=
stopień zbrojenia przekroju
obliczeniowa nosność na ścinanie
elementów bez zbrojenia
VRd.c
CRd.c k
100
ρL
fck
MPa
1
3
hr
dy
MPa
194.565 kN
=
:=
VRd.c.min
νmin hr
dy
169.181 kN
=
:=
VRd.c VEd.y
>
1
=
WARUN EK SP EŁNIONY- nie wym agane wymiarowanie zbrojenia na
ścinanie
Sprawdzenie warunku na Vb
fywd
fyd 434.783 MPa
=
:=
obliczeniowa granica plastyczności
dy 0.541 m
=
wysokość użyteczna przekroju
szerokość rygla
hr 0.8 m
=
współczynnik redukcji wytzrym ałości
betonu zarysowanego przy ścinaniu
ν
0.6 1
fck
250MPa
-
0.528
=
:=
Vb
0.5 hr
dy
ν
fcd
2.448
10
3
kN
=
:=
Vb VEd.y
>
1
=
WARUN EK SP EŁNIONY - krzyżulce betonowe nie ulegną zmiażdżeniu
Przyjęcie zbrojenia konstrukcyjnego:
ϕs
8mm
:=
średnica strzem ion
Asw
2
π
ϕs
2
2
1.005 cm
2
=
:=
pole przekroju zbrojenia na ścianie
(strzem iona 2-cięte)
s1
12.5cm
:=
dobrany rozstaw strzem ion
sI.max
0.75dx 55.463 cm
=
:=
m aksym alny rozstaw strzemion
s1 sI.max
<
1
=
WARUN EK SP EŁNIONY
ρw.min
0.08
fck MPa
1
-
fyk MPa
1
-
0.088 %
=
:=
m inimalny stopień zbrojenia
ρw
Asw
hr s1
0.101 %
=
:=
stopień zbrojenia

ρw ρw.min
>
1
=
WARUN EK SP EŁNIONY
8. Wymiarowanie słupa
8.1. Dane i założenia
bs 0.6 m
=
szerokość słupa
hs 0.6 m
=
wysokość słupa
Lcol 6.8 m
=
długość obliczeniowa słupa
βx
2
:=
βy
2
:=
współczynniki wyboczeniowe
mx
1
:=
my
1
:=
liczba elem entów pionowych wpływających na
rozpatrywany efekt
ϕ
32mm
:=
przyjęta średnica zbrojenia głównego
n
16
:=
przyjęta liczba pretów
As
n
π ϕ
2
4
128.68 cm
2
=
:=
pole przyjętego zbrojenia
ϕs 8 mm
=
przyjęta średnica strzemion
cnom 40 mm
=
otulenie zbrojenia
d
bs cnom
-
ϕs
-
0.5
ϕ
-
53.6 cm
=
:=
wysokość użyteczna w płaszczyżnie x i y
a1
cnom ϕs
+
0.5
ϕ
+
6.4 cm
=
:=
odległość środka ciężkości zbrojenia od
krawędzi
a2
a1 6.4 cm
=
:=
8.2.1 I kombinacją: Maksymalny M.x i wartości odpowiadające
Mx.s
664.11kN m
:=
MEd.x
Mx.s 664.11 kN m
=
:=
obliczeniowy m om ent zginający
(pł.x, dół słupa)
My.s
195.228kN m
:=
MEd.y
My.s 195.228 kN m
=
:=
obliczeniowy m om ent zginający
(pł.y, dół słupa)
Ns
561.09kN
:=
NEd
Ns 561.09 kN
=
:=
obliczeniowa siła ściskająca (dół słupa)
8.2.2 Zbrojenie minimalne i maksymalne dla słupa
As.min
max
0.1NEd
fyd
0.002 hs
bs
,
7.2 cm
2
=
:=
zbrojenie m inimalne
As.max
4% bs
hs
144 cm
2
=
:=
zbrojenie m aksym alne
8.2.3 Inperfekcje geometryczne
Θo
1
200
0.005
=
:=
wartość bazowa

αh
2
Lcol
m
0.767
=
:=
2
3
αh
<
1
<
1
=
WARUN EK SP EŁNIONY. współczynnik
redukujący wysokość
αm
0.5 1
1
mx
+
1
=
:=
współczynnik redukcyjny ze względu na liczbę
elementów
Θl
Θo αh
αm
0.004
=
:=
kąt pochylenia
l0.x
βx Lcol
13.6 m
=
:=
l0.y
l0.x 13.6 m
=
:=
długości efektywne słupa
ei.x
Θl l0.x
2
26.077 mm
=
:=
ei.y
ei.x 26.077 mm
=
:=
m im ośród imperfekcji
ee.x
MEd.x
NEd
1183.607 mm
=
:=
m im ośród I rzędu w pł. x
ee.y
MEd.y
NEd
347.944 mm
=
:=
m im ośród I rzędu w pł. y
e0.x
max 20mm ei.x ee.x
+
,
bs
30
,
120.968 cm
=
:=
e0.y
max 20mm ei.y ee.y
+
,
hs
30
,
37.402 cm
=
:=
8.2.4. Współczynnik pełzania
8.2.4.1. Końcowy współczynnik pełzania
Ac
bs hs
3.6
10
3
cm
2
=
:=
pole przekroju słupa
u
2 bs hs
+
(
)
240 cm
=
:=
obwód elementu kontaktującego się z atmosferą
h0
2 Ac
u
30 cm
=
:=
m iarodajny wymiar elementu
RH
50
:=
wilgotność względna powietrza (%)
Δt
28
:=
wiek betonu w chwili obciążenia (dni)
TΔt
15
:=
temperatura dojrzewania betonu (st. cel.)
α1
35MPa
fcm
0.7
0.944
=
:=
współczynniki zależne od wytrzymałości betonu
α2
35 MPa
fcm
0.2
0.984
=
:=

współczynnik zależny od wpływu wilgotności
względnej na podstawie współczynnika pełzania
ϕRH
1
1
RH
100
-
0.1
3
h0 cm
1
-
α1
+
α2
2.478
=
:=
βfcm
16.8
fcm MPa
1
-
2.725
=
:=
wiek betonu dostosowany do temperatury
dojrzewania 15 st. C przez 28 dni
t0.T
Δt e
4000
273 TΔt
+
13.65
-
-
22.05
=
:=
α
0
:=
wykładnik potegowy dla cemnetu klasy N
t0
max t0.T
9
2
t0.T
1.2
+
1
+
α
0.5
,
22.05
=
:=
wiek betonu z uwzględnieniem rodzaju cementu
βt.0
1
0.1
t0
0.2
+
0.511
=
:=
współczynnik zależny od wieku betonu w chwili
obciążenia
ϕoo.to
ϕRH βfcm
βt.0
3.452
=
:=
końcowy współczynnik pełzania
8.2.4.2 Efektywny współczynnik pełzania
obliczeniowa siła od prawie stałych obciążeń
(długotrwałych)
NE.g
0.8 NEd
448.872 kN
=
:=
ME.g.x
0.8MEd.x 531.288 kN m
=
:=
γGsup
1.35
:=
współczynnik od obciążeń stałych
ME.qp.x
ME.g.x
γGsup
393.547 kN m
=
:=
charakterystyczny mom ent od prawie stałych
obciążeń długotrwałych
NE.qp.x
NE.g
γGsup
332.498 kN
=
:=
charakterystyczna siła od prawie stałych obciążeń
M0.E.qp.x
ME.qp.x NE.qp.x ei.x
+
402.217 kN m
=
:=
charakterystyczny mom ent I rzędu od prawie
stałych obciążeń
M0.Ed.x
MEd.x NEd ei.x
+
678.741 kN m
=
:=
obliczeniowy m om ent I rzędu od wszystkich
obciążeń
ϕef
ϕoo.to
M0.E.qp.x
M0.Ed.x
2.046
=
:=
efektywny współczynnik pełzania
M0.E.qp.x
M0.Ed.x
0.593
=
0.8
γGsup
0.593
=
W drugiej płaszczyźnie wartość efektywnego współczynnika jest taka sam a
8.2.5 Sprawdzenie czy należy uwzględnić efekty II rzędu

Płaszczyzna x
Ac
bs hs
3.6
10
3
cm
2
=
:=
pole przekroju słupa
Ic.x
bs hs
3
12
1.08
10
6
cm
4
=
:=
m oment bezwładności przekroju słupa
ix
Ic.x
Ac
17.321 cm
=
:=
promień bezwładności
λx
βx Lcol
ix
78.52
=
:=
sm ukłość słupa
A
1
1
0.2
ϕef
+
0.71
=
:=
ω
As fyd
Ac fcd
0.725
=
:=
m oc zbrojenia (pole przekroju zbrojenia podłużnego)
B
1
2
ω
+
1.565
=
:=
rm
1
:=
C
1.7
rm
-
0.7
=
:=
na
NEd
Ac fcd
0.073
=
:=
względna siła normalna
λlim.x
20 A
B
C
na
57.669
=
:=
sm ukłośc graniczna
λx λlim.x
>
1
=
słup smukły - należy uwzględnić efekty II rzędu
Płaszczyzna y
Ac
bs hs
3.6
10
3
cm
2
=
:=
pole przekroju słupa
Ic.y
bs hs
3
12
1.08
10
6
cm
4
=
:=
m oment bezwładności przekroju słupa
iy
Ic.y
Ac
17.321 cm
=
:=
promień bezwładności
λy
βy Lcol
iy
78.52
=
:=
sm ukłość słupa
A
1
1
0.2
ϕef
+
0.71
=
:=
ω
As fyd
Ac fcd
0.725
=
:=
m oc zbrojenia (pole przekroju zbrojenia podłużnego)
B
1
2
ω
+
1.565
=
:=
:=
-
=
:=
rm
1
:=
C
1.7
rm
-
0.7
=
:=
na
NEd
Ac fcd
0.073
=
:=
względna siła normalna
λlim.x
20 A
B
C
na
57.669
=
:=
sm ukłośc graniczna
λx λlim.x
>
1
=
słup smukły - należy uwzględnić efekty II rzędu
8.2.6. Analiz a II rzędu - m etoda nominalnej krzywiz ny
Płaszczyzna x
na
NEd
Ac fcd
0.073
=
:=
względna siła normalna
wartość dla której osiąga się m aksymalny mom ent
graniczny, m ożna przyjm ować =0,4
nbal
0.4
:=
ω
As fyd
Ac fcd
0.725
=
:=
m oc zbrojenia (pole przekroju zbrojenia podłużnego)
nu
1
ω
+
1.725
=
:=
Kr
min 1
nu na
-
nu nbal
-
,
1
=
:=
współczynnik poprawkowy zależny od siły podłużnej
β'
0.35
fck
200 MPa
+
λx
150
+
1.023
=
:=
Kϕ
max 1
β' ϕef
+
1
,
(
)
3.094
=
:=
współczynnik uwzględniający pełzanie
εyd
fyd
Es
2.174
10
3
-
=
:=
As2.x
As1.x
:=
As1.x
7
π ϕ
2
4
56.297 cm
2
=
:=
pole przekroju zbrojenia w płaszczyznie x
As.x
As1.x As2.x
+
85.554 cm
2
=
:=
m oment bezwładności całkowitego zbrojenia słupa względem środka ciężkości
Is.x
n
π ϕ
4
64
As.x 0.5bs a1
-
(
)
2
+
4
π ϕ
2
4
0.5 bs
a1
-
10cm
-
(
)
2
+
5.368
10
4
cm
4
=
:=
is
Is.x
n
π ϕ
2
4
20.425 cm
=
:=
promień bezwładności
d
53.6 cm
=
d'
bs
2
is
+
50.425 cm
=
:=
skorygowana wysokość użyteczna
ro
0.45 d'
εyd
104.38 m
=
:=
1
ro
9.58
10
3
-
1
m
=
krzywizna elem entów o sym etrycznym przekroju
poprzecznym ( włączając zbrojenie)
r
ro
Kr Kϕ
33.741 m
=
:=
1
r
0.03
1
m
=
c
10
:=
przekrój poprzczny stały
e2.x
1
r
l0.x
2
c
54.818 cm
=
:=
m im ośród II rzędu w płaszczyźnie x
etot.x
e0.x e2.x
+
175.786 cm
=
:=
m im ośród całkowity ( I i II rzędu + przypadkowy)
MEd.x.tot
NEd etot.x
986.318 kN m
=
:=
m oment całkowity
Płaszczyzna y
na
NEd
Ac fcd
0.073
=
:=
względna siła normalna
wartość dla której osiąga się m aksymalny mom ent
graniczny, m ożna przyjm ować =0,4
nbal
0.4
:=
ω
As fyd
Ac fcd
0.725
=
:=
m oc zbrojenia (pole przekroju zbrojenia podłużnego)
nu
1
ω
+
1.725
=
:=
Kr
min 1
nu na
-
nu nbal
-
,
1
=
:=
współczynnik poprawkowy zależny od siły podłużnej
β'
0.35
fck
200 MPa
+
λy
150
+
1.023
=
:=
Kϕ
max 1
β' ϕef
+
1
,
(
)
3.094
=
:=
współczynnik uwzględniający pełzanie
εyd
fyd
Es
0.002
=
:=
As1.y
8
π ϕ
2
4
64.34 cm
2
=
:=
As2.y
As1.y
:=
pole przekroju zbrojenia w płaszczyznie y
As.y
As1.y As2.y
+
128.68 cm
2
=
:=
m oment bezwładności całkowitego zbrojenia słupa względem środka ciężkości
Is.y
n
π ϕ
4
64
As.y 0.5hs a1
-
(
)
2
+
4
π ϕ
2
4
0.5 hs
a1
-
10cm
-
(
)
2
+
7.77
10
4
cm
4
=
:=
is
Is.y
n
π ϕ
2
4
0.246 m
=
:=
promień bezwładności
d
53.6 cm
=
d'
hs
2
is
+
54.573 cm
=
:=
skorygowana wysokość użyteczna
ro
0.45 d'
εyd
112.966 m
=
:=
1
ro
0.009
1
m
=
krzywizna elem entów o sym etrycznym przekroju
poprzecznym ( włączając zbrojenie)
r
ro
Kr Kϕ
36.517 m
=
:=
1
r
0.027
1
m
=
c
10
:=
przekrój poprzeczny stały
e2.y
1
r
l0.y
2
c
50.651 cm
=
:=
m im ośród II rzędu w płaszczyźnie y
etot.y
e0.y e2.y
+
88.053 cm
=
:=
m im ośród całkowity ( I i II rzędu + przypadkowy)
MEd.y.tot
NEd etot.y
494.057 kN m
=
:=
m oment całkowity
8.2.6.1. Sprawdzenie czy słup należy projektować jako jedno czy dwukierunkowo
zbrojony
λx 78.52
=
λy 78.52
=
λx
λy
1
=
λx
λy
2
<
1
=
λy
λx
1
=
λy
λx
2
<
1
=
WARUN KI
SPEŁNIONE
WARUN IKI NIE
SPEŁNIONE
etot.x
bs
etot.y
hs
1.996
=
etot.x
bs
etot.y
hs
0.2
<
0
=
etot.y
hs
etot.x
bs
0.501
=
etot.y
hs
etot.x
bs
0.2
<
0
=
SŁUP DWUKIERUNKOWO ZBROJONY
8.2.6.2 Nośność słupa
8.2.6.2.1 Nośność MRd dla płaszczyzny x - przy znanej sile ściskającej
ξeff
NEd fyd As2.x
-
fyd As1.x
+
fcd bs
d
0.252
=
:=
ξeff.lim 0.493
=
ξ'eff
NEd
2
1
ξeff.lim
-
1
-
fyd
As1.x
+
fyd As2.x
-
fcd bs
d
2
1
ξeff.lim
-
fyd
As1.x
+
0.393
=
:=
ξ''eff
NEd fyd As2.x
-
fyd As1.x
-
fcd bs
d
0.458
-
=
:=
ξeff ξeff.lim
<
1
=
ξeff 0.252
=
es2
fyd As1.x
d
a2
-
(
)
NEd
205.906 cm
=
:=
es1
fcd bs
d
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.x
d
a2
-
(
)
+
NEd
252.01 cm
=
:=

ξeff
2 a2
d
<
0
=
MRd.x
fyd As1.x
d
a2
-
(
)
NEd
bs
2
a2
-
+
1.288
10
3
kN m
=
:=
MEd.x.tot 986.318 kN m
=
8.2.6.2.2 Nośność MRd dla płaszczyzny y - przy znanej sile ściskającej
ξeff
NEd fyd As2.y
-
fyd As1.y
+
fcd hs
d
0.081
=
:=
ξeff.lim 0.493
=
ξ'eff
NEd
2
1
ξeff.lim
-
1
-
fyd
As1.y
+
fyd As2.y
-
fcd hs
d
2
1
ξeff.lim
-
fyd
As1.y
+
0.335
=
:=
ξ''eff
NEd fyd As2.y
-
fyd As1.y
-
fcd hs
d
0.73
-
=
:=
ξeff ξeff.lim
<
1
=
ξeff 0.081
=
es2
fyd As1.y
d
a2
-
(
)
NEd
235.321 cm
=
:=
es1
fcd hs
d
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.y
d
a2
-
(
)
+
NEd
286.739 cm
=
:=
ξeff
2 a2
d
<
1
=
MRd.y
fyd As1.y
d
a2
-
(
)
NEd
hs
2
a2
-
+
1.453
10
3
kN m
=
:=
MEd.y.tot 494.057 kN m
=
ZESTAWIEN IE WYN IKÓW:
NEd 561.09 kN
=
MEd.x.tot 986.318 kN m
=
MEd.y.tot 494.057 kN m
=
MRd.x 1.288 10
3
kN m
=
MRd.y 1.453 10
3
kN m
=
MRd.x MEd.x.tot
>
1
=
MRd.y MEd.y.tot
>
1
=
8.2.6.2.3 Określenie nośności słupa osiowo ściskanego
n
16
=
liczba pętów
As.cal
n
π ϕ
2
4
128.68 cm
2
=
:=
powierzchnia prętów zbrojenia

Nośność obliczeniowa słupa
ściskanego
NRd.0
bs hs
As.cal
-
(
)
fcd As.cal fyd
+
1.303
10
4
kN
=
:=
NEd
NRd.0
0.043
=
a
1
:=
wg Tabela pkt.5.8.9 EC-2
8.2.6.2.4. Określenie nośności słupa dwukierunkowo zginanego:
MEd.x.tot
MRd.x
a
MEd.y.tot
MRd.y
a
+
1.106
=
MEd.x.tot
MRd.x
a
MEd.y.tot
MRd.y
a
+
1
0
=
8.2.7 Analiza II rzędu - metoda nominalnej sztyw ności
Nominalna sztywność - płaszczyzna x
γCE
1.2
:=
Ic.x 1.08 10
6
cm
4
=
Ecd
Ecm
γCE
27.364 GPa
=
:=
Is.x 5.368 10
4
cm
4
=
ρx
As
Ac
3.574 %
=
:=
ρx 0.002
1
=
stopień zbrojenia
k1
fck
20 MPa
1.225
=
:=
współczynnik zależny od klasy cementu
n
NEd
Ac fcd
0.073
=
:=
względna siła podłużna
λx 78.52
=
sm ukłość słupa
współczynnik zależny od siły osiowej i smukłości
słupa
k2
min n
λx
170
0.2
,
0.034
=
:=
Ks
1
:=
współczynnik wyrażający udział zbrojenia
Kc
k1 k2
1
ϕef
+
0.014
=
:=
współczynnik wyrażąjący efekty zarysowania,
pełzania, itp.
EI
Kc Ecd
Ic.x
Ks Es
Is.x
+
111.358 MN m
2
=
:=
nom inalna sztywność sm ukłych elementów
ściskanych
NB.x
π
2
l0.x
2
EI
5.942
10
3
kN
=
:=
nośność przy wyboczeniu ustalona prze założeniu
sztywności nom inalnej
co
8
:=
współczynnik zależny od rozkładu m omentu
β'
π
2
co
1.234
=
:=
założenie sinusoiealnego rozkładu m omentu I rzędu
M0.Ed.x
MEd.x NEd ei.x
+
678.741 kN m
=
:=
m oment I rzędu uwzględniający efekty im perfekcji
MEd.x.tot
M0.Ed.x 1
β'
NB.x
NEd
1
-
+
766.055 kN m
=
:=
m oment całkowity
etot.x
MEd.x.tot
NEd
136.53 cm
=
:=
m im ośród całkowity
Nominalna sztywność - płaszczyzna y
γCE
1.2
:=
Ic.y 1.08 10
6
cm
4
=
Ecd
Ecm
γCE
27.364 GPa
=
:=
Is.y 7.77 10
4
cm
4
=
ρy
As
Ac
3.574 %
=
:=
ρy 0.002
1
=
stopień zbrojenia
k1
fck
20 MPa
1.225
=
:=
współczynnik zależny od klasy cementu
n
NEd
Ac fcd
0.073
=
:=
względna siła podłużna
λy 78.52
=
sm ukłość słupa
współczynnik zależny od siły osiowej i smukłości
słupa
k2
min n
λy
170
0.2
,
0.034
=
:=
Ks
1
:=
współczynnik wyrażający udział zbrojenia
Kc
k1 k2
1
ϕef
+
0.014
=
:=
współczynnik wyrażąjący efekty zarysowania,
pełzania, itp.
EI
Kc Ecd
Ic.y
Ks Es
Is.y
+
159.396 MN m
2
=
:=
nom inalna sztywność sm ukłych elementów
ściskanych
NB.y
π
2
l0.y
2
EI
8505.507 kN
=
:=
nośność przy wyboczeniu ustalona prze założeniu
sztywności nom inalnej
co
12
:=
współczynnik zależny od rozkładu m omentu
β'
π
2
co
0.822
=
:=
założenie sinusoiealnego rozkładu m omentu I rzędu
M0.Ed.y
MEd.y NEd ei.y
+
209.859 kN m
=
:=
m oment I rzędu uwzględniający efekty im perfekcji
MEd.y.tot
M0.Ed.y 1
β'
NB.y
NEd
1
-
+
222.05 kN m
=
:=
m oment całkowity
etot.y
MEd.y.tot
NEd
39.575 cm
=
:=
m im ośród całkowity
8.2.7.1. Sprawdzenie czy słup należy projektować jako jedno czy dwukierunkowo
zbrojony
λx 78.52
=
λy 78.52
=
λx
λy
1
=
λx
λy
2
<
1
=
λy
λx
1
=
λy
λx
2
<
1
=
WARUN KI
SPEŁNIONE
WARUN IKI NIE
SPEŁNIONE
etot.x
bs
etot.y
hs
3.45
=
etot.x
bs
etot.y
hs
0.2
<
0
=
etot.y
hs
etot.x
bs
0.29
=
etot.y
hs
etot.x
bs
0.2
<
0
=
SŁUP DWUKIERUNKOWO ZBROJONY
8.2.7.2 Nośność słupa
8.2.7.2.1 Nośność MRd dla płaszczyzny x - przy znanej sile ściskającej
ξeff
NEd fyd As2.x
-
fyd As1.x
+
fcd bs
d
0.252
=
:=
ξeff.lim 0.493
=
ξ'eff
NEd
2
1
ξeff.lim
-
1
-
fyd
As1.x
+
fyd As2.x
-
fcd bs
d
2
1
ξeff.lim
-
fyd
As1.x
+
0.393
=
:=
ξ''eff
NEd fyd As2.x
-
fyd As1.x
-
fcd bs
d
0.458
-
=
:=
ξeff ξeff.lim
<
1
=
ξeff 0.252
=
-
(
)
es2
fyd As1.x
d
a2
-
(
)
NEd
205.906 cm
=
:=
es1
fcd bs
d
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.x
d
a2
-
(
)
+
NEd
252.01 cm
=
:=
ξeff
2 a2
d
<
0
=
MRd.x
fcd hs
dx
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.x
dx a2
-
(
)
+
NEd
bs
2
a1
-
-
2.276
10
3
kN m
=
:=
MEd.x.tot 766.055 kN m
=
8.2.7.2.2 Nośność MRd dla płaszczyzny y - przy znanej sile ściskającej
ξeff
NEd fyd As2.y
-
fyd As1.y
+
fcd hs
d
0.081
=
:=
ξeff.lim 0.493
=
ξ'eff
NEd
2
1
ξeff.lim
-
1
-
fyd
As1.y
+
fyd As2.y
-
fcd hs
d
2
1
ξeff.lim
-
fyd
As1.y
+
0.335
=
:=
ξ''eff
NEd fyd As2.y
-
fyd As1.y
-
fcd hs
d
0.73
-
=
:=
ξeff ξeff.lim
<
1
=
ξeff 0.081
=
es2
fyd As1.y
d
a2
-
(
)
NEd
235.321 cm
=
:=
es1
fcd hs
d
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.y
d
a2
-
(
)
+
NEd
286.739 cm
=
:=
ξeff
2 a2
d
<
1
=
MRd.y
fyd As1.y
d
a2
-
(
)
NEd
hs
2
a2
-
+
1.453
10
3
kN m
=
:=
MEd.y.tot 222.05 kN m
=
ZESTAWIEN IE WYN IKÓW:
NEd 561.09 kN
=
MEd.x.tot 766.055 kN m
=
MEd.y.tot 222.05 kN m
=
MRd.x 2.276 10
3
kN m
=
MRd.y 1.453 10
3
kN m
=
MRd.x MEd.x.tot
>
1
=
MRd.y MEd.y.tot
>
1
=
8.2.7.2.3 Określenie nośności słupa osiowo ściskanego
n
24
:=
liczba pętów
As.cal
n
π ϕ
2
4
193.019 cm
2
=
:=
powierzchnia prętów zbrojenia
nośność obliczeniowa słupa
ściskanego
NRd.0
bs hs
As.cal
-
(
)
fcd As.cal fyd
+
1.569
10
4
kN
=
:=
NEd
NRd.0
0.036
=
a
1
:=
wg Tabela pkt.5.8.9 EC-2
8.2.7.2.4. Określenie nośności słupa dwukierunkowo ściskanego:
MEd.x.tot
MRd.x
a
MEd.y.tot
MRd.y
a
+
0.489
=
MEd.x.tot
MRd.x
a
MEd.y.tot
MRd.y
a
+
1
1
=
8.3.1 II kombinacją: Maksymalny M.y i wartości odpowiadające
My.s
585.684kN m
:=
MEd.y
My.s 585.684 kN m
=
:=
obliczeniowy m om ent zginający
(pł.y, dół słupa)
Mx.s
284.61kN m
:=
MEd.x
Mx.s 284.61 kN m
=
:=
obliczeniowy m om ent zginający
(pł.x, dół słupa)
Ns
891.09kN
:=
NEd
Ns 891.09 kN
=
:=
obliczeniowa siła ściskająca (dół słupa)
8.3.1.1 Anali za II rz ędu - metoda nominal nej sztywności
Nominalna sztywność - płaszczyzna x
γCE
1.2
:=
Ic.x 1.08 10
6
cm
4
=
Ecd
Ecm
γCE
27.364 GPa
=
:=
Is.x 5.368 10
4
cm
4
=
ρx
As
Ac
3.574 %
=
:=
ρx 0.002
1
=
stopień zbrojenia
k1
fck
20 MPa
1.225
=
:=
współczynnik zależny od klasy cementu
n
NEd
Ac fcd
0.116
=
:=
względna siła podłużna
λx 78.52
=
sm ukłość słupa
współczynnik zależny od siły osiowej i smukłości
słupa
k2
min n
λx
170
0.2
,
0.053
=
:=
Ks
1
:=
współczynnik wyrażający udział zbrojenia
Kc
k1 k2
1
ϕef
+
0.021
=
:=
współczynnik wyrażąjący efekty zarysowania,
pełzania, itp.
EI
Kc Ecd
Ic.x
Ks Es
Is.x
+
113.706 MN m
2
=
:=
nom inalna sztywność sm ukłych elementów
ściskanych
NB.x
π
2
l0.x
2
EI
6.067
10
3
kN
=
:=
nośność przy wyboczeniu ustalona prze założeniu
sztywności nom inalnej
co
8
:=
współczynnik zależny od rozkładu m omentu
β'
π
2
co
1.234
=
:=
założenie sinusoiealnego rozkładu m omentu I rzędu
M0.Ed.x
MEd.x NEd ei.x
+
307.847 kN m
=
:=
m oment I rzędu uwzględniający efekty im perfekcji
MEd.x.tot
M0.Ed.x 1
β'
NB.x
NEd
1
-
+
373.227 kN m
=
:=
m oment całkowity
etot.x
MEd.x.tot
NEd
41.884 cm
=
:=
m im ośród całkowity
Nominalna sztywność - płaszczyzna y
γCE
1.2
:=
Ic.y 1.08 10
6
cm
4
=
Ecd
Ecm
γCE
27.364 GPa
=
:=
Is.y 7.77 10
4
cm
4
=
ρy
As
Ac
3.574 %
=
:=
ρy 0.002
1
=
stopień zbrojenia
k1
fck
20 MPa
1.225
=
:=
współczynnik zależny od klasy cementu
n
NEd
Ac fcd
0.116
=
:=
względna siła podłużna
λy 78.52
=
sm ukłość słupa
współczynnik zależny od siły osiowej i smukłości
słupa
k2
min n
λy
170
0.2
,
0.053
=
:=
Ks
1
:=
współczynnik wyrażający udział zbrojenia
Kc
k1 k2
1
ϕef
+
0.021
=
:=
współczynnik wyrażąjący efekty zarysowania,
pełzania, itp.
EI
Kc Ecd
Ic.y
Ks Es
Is.y
+
161.744 MN m
2
=
:=
nom inalna sztywność sm ukłych elementów
ściskanych
NB.y
π
2
l0.y
2
EI
8.631
10
3
kN
=
:=
nośność przy wyboczeniu ustalona prze założeniu
sztywności nom inalnej
co
12
:=
współczynnik zależny od rozkładu m omentu
β'
π
2
co
0.822
=
:=
założenie sinusoiealnego rozkładu m omentu I rzędu
M0.Ed.y
MEd.y NEd ei.y
+
608.921 kN m
=
:=
m oment I rzędu uwzględniający efekty im perfekcji
MEd.y.tot
M0.Ed.y 1
β'
NB.y
NEd
1
-
+
666.581 kN m
=
:=
m oment całkowity
etot.y
MEd.y.tot
NEd
74.805 cm
=
:=
m im ośród całkowity
8.3.1.2. Sprawdzenie czy słup należy projektować jako jedno czy dwukierunkowo
zbrojony
λx 78.52
=
λy 78.52
=
λx
λy
1
=
λx
λy
2
<
1
=
λy
λx
1
=
λy
λx
2
<
1
=
WARUN KI
SPEŁNIONE
WARUN IKI NIE
SPEŁNIONE
etot.x
bs
etot.y
hs
0.56
=
etot.x
bs
etot.y
hs
0.2
<
0
=
etot.y
hs
etot.x
bs
1.786
=
etot.y
hs
etot.x
bs
0.2
<
0
=
SŁUP DWUKIERUNKOWO ZBROJONY
8.3.1.3 Nośność słupa
8.3.1.3.1 Nośność MRd dla płaszczyzny x - przy znanej sile ściskającej
ξeff
NEd fyd As2.x
-
fyd As1.x
+
fcd bs
d
0.3
=
:=
ξeff.lim 0.493
=

ξ'eff
NEd
2
1
ξeff.lim
-
1
-
fyd
As1.x
+
fyd As2.x
-
fcd bs
d
2
1
ξeff.lim
-
fyd
As1.x
+
0.413
=
:=
ξ''eff
NEd fyd As2.x
-
fyd As1.x
-
fcd bs
d
0.41
-
=
:=
ξeff ξeff.lim
<
1
=
ξeff 0.3
=
es2
fyd As1.x
d
a2
-
(
)
NEd
129.652 cm
=
:=
es1
fcd bs
d
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.x
d
a2
-
(
)
+
NEd
173.054 cm
=
:=
ξeff
2 a2
d
<
0
=
MRd.x
fcd hs
dx
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.x
dx a2
-
(
)
+
NEd
bs
2
a1
-
-
2.441
10
3
kN m
=
:=
MEd.x.tot 373.227 kN m
=
8.3.1.3.2 Nośność MRd dla płaszczyzny y - przy znanej sile ściskającej
ξeff
NEd fyd As2.y
-
fyd As1.y
+
fcd hs
d
0.129
=
:=
ξeff.lim 0.493
=
ξ'eff
NEd
2
1
ξeff.lim
-
1
-
fyd
As1.y
+
fyd As2.y
-
fcd hs
d
2
1
ξeff.lim
-
fyd
As1.y
+
0.354
=
:=
ξ''eff
NEd fyd As2.y
-
fyd As1.y
-
fcd hs
d
0.683
-
=
:=
ξeff ξeff.lim
<
1
=
ξeff 0.129
=
es2
fyd As1.y
d
a2
-
(
)
NEd
148.174 cm
=
:=
es1
fcd hs
d
2
ξeff
1
0.5
ξeff
-
(
)
fyd As2.y
d
a2
-
(
)
+
NEd
198.309 cm
=
:=
ξeff
2 a2
d
<
1
=

MRd.y
fyd As1.y
d
a2
-
(
)
NEd
hs
2
a2
-
+
1.531
10
3
kN m
=
:=
MEd.y.tot 666.581 kN m
=
ZESTAWIEN IE WYN IKÓW:
NEd 891.09 kN
=
MEd.x.tot 373.227 kN m
=
MEd.y.tot 666.581 kN m
=
MRd.x 2.441 10
3
kN m
=
MRd.y 1.531 10
3
kN m
=
MRd.x MEd.x.tot
>
1
=
MRd.y MEd.y.tot
>
1
=
8.3.1.4 Określenie nośności słupa osiowo ściskanego
n
24
:=
liczba pętów
As.cal
n
π ϕ
2
4
193.019 cm
2
=
:=
powierzchnia prętów zbrojenia
Nośność obliczeniowa słupa
ściskanego
NRd.0
bs hs
As.cal
-
(
)
fcd As.cal fyd
+
1.569
10
4
kN
=
:=
NEd
NRd.0
0.057
=
a
1
:=
wg Tabela pkt.5.8.9 EC-2
8.3.1.5. Określenie nośności słupa dwukierunkow ściskanego:
MEd.x.tot
MRd.x
a
MEd.y.tot
MRd.y
a
+
0.588
=
MEd.x.tot
MRd.x
a
MEd.y.tot
MRd.y
a
+
1
1
=
8.4. Zbrojenie na skręcanie i ścinanie
8.4.1 I. kombinacja (maksymalny moment skręcający i odpowiadająca siła ścinająca)
Mz.s
160.776kN m
:=
TEd
Mz.s 160.776 kN m
=
:=
Qy.s
28.71kN
:=
VEd
Qy.s 28.71 kN
=
:=
Sprawdzenie czy zbrojenie na ścinanie i skręcanie jest konieczne
CRd.c
0.18
γc
0.129
=
:=
k
min 1
200mm
d
+
2
,
1.611
=
:=
AsL
As.x 85.554 cm
2
=
:=
ρL
min
AsL
bs dx
2%
,
1.928 %
=
:=
k1
0.15
:=
σcp
0MPa
:=
νmin
0.035 k
3
2
fck
MPa
1
2
MPa
0.392 MPa
=
:=

VRd.c
CRd.c k
100
ρL
fck
MPa
1
3
MPa
k1 σcp
+
bs
dx
355.395 kN
=
:=
VRd.c
νmin k1 σcp
+
(
)
bs
dx
>
1
=
WARUN EK SP EŁNIONY
VRd.c 355.395 kN
=
>
VEd 28.71 kN
=
NIE POTRZEBA ZBROJENIA NA
ŚCINANIE
tef
max 2 a1
bs hs
2 bs hs
+
(
)
,
0.15 m
=
:=
Ak
bs tef
-
(
)
hs tef
-
(
)
2.025
10
3
cm
2
=
:=
uk
2 bs tef
-
hs
+
tef
-
(
)
1.8 m
=
:=
TRd.c
2 Ak
tef
fctd
86.786 kN m
=
:=
TRd.c TEd
<
1
=
Należy zastosować zbrojenie na
skręcania
Maksym alna siła ściskająca ściankę:
τT
TEd
2 Ak
tef
2.647 MPa
=
:=
τV
VEd
bs 0.9 dx
(
)
0.072 MPa
=
:=
VEd.i
τT τV
+
(
)
tef
hs tef
-
(
)
183.493 kN
=
:=
Asw
π ϕs
2
4
0.503 cm
2
=
:=
ν
0.6 1
fck
250MPa
-
0.528
=
:=
αcw
1
:=
θ
1
2
asin
2 VEd.i
αcw ν
fcd
tef
hs tef
-
(
)
14.36 deg
=
:=
cot
θ
( )
3.906
=
>
2
Przyjęto:
θ
26.6deg
:=
cot
θ
( )
1.997
=
fywd
fyd
:=
s1
Asw
VEd.i
hs tef
-
(
)
fywd
cot
θ
( )
10.703 cm
=
:=
przyjęto rozstaw:
s1
10cm
:=
VRd.s.i
Asw
s1
hs tef
-
(
)
fywd
cot
θ
( )
196.391 kN
=
:=
VRd.s.i VEd.i
>
1
=
VRd.max.i
αcw tef
hs tef
-
(
)
ν
fcd
cot
θ
( )
tan
θ
( )
+
305.765 kN
=
:=
VRd.max.i VEd.i
>
1
=
TRd.max
2
ν
αcw
fcd
Ak
tef
sin
θ
( )
cos
θ
( )
275.188 kN m
=
:=
VRd.max
αcw bs
0.9
dx
ν
fcd
cot
θ
( )
tan
θ
( )
+
1.809
10
3
kN
=
:=

TEd
TRd.max
VEd
VRd.max
+
0.6
=
<
1
WARUN EK SP EŁNIONY
Wymagane pole przekroju zbrojenia podłużnego na skręcanie:
ASL
TEd
2 Ak
uk
fyd
cot
θ
( )
32.82 cm
2
=
:=
ASL As
<
1
=
Nie trzeba przyjmować dodatkowego zbrojenia podłużnego
Sprawdzenie warunków na m inim alny stopień zbrojenia oraz warunków konstrukcyjnych:
ρw
2Asw
s1 bs
0.168 %
=
:=
ρw.min
0.08
fck MPa
1
-
fyk MPa
1
-
0.088 %
=
:=
ρw ρw.min
>
1
=
smax
min 0.75 dx
bs
,
uk
8
,
22.5 cm
=
:=
s1 smax
<
1
=
WARUN EK SP EŁNIONY
8.4.2 II. kombinacja (maksymalna siłą ścinająca i odpowiadający moment skręcający)
Mz.s
28.71kN m
:=
TEd
Mz.s 28.71 kN m
=
:=
Qy.s
86.13kN
:=
VEd
Qy.s 86.13 kN
=
:=
Sprawdzenie czy zbrojenie na ścinanie i skręcanie jest konieczne
CRd.c
0.18
γc
0.129
=
:=
k
min 1
200mm
d
+
2
,
1.611
=
:=
AsL
As.x 85.554 cm
2
=
:=
ρL
min
AsL
bs dx
2%
,
1.928 %
=
:=
k1
0.15
:=
σcp
0MPa
:=
νmin
0.035 k
3
2
fck
MPa
1
2
MPa
0.392 MPa
=
:=
VRd.c
CRd.c k
100
ρL
fck
MPa
1
3
MPa
k1 σcp
+
bs
dx
355.395 kN
=
:=
VRd.c
νmin k1 σcp
+
(
)
bs
dx
>
1
=
WARUN EK SP EŁNIONY
VRd.c 355.395 kN
=
>
VEd 86.13 kN
=
NIE POTRZEBA ZBROJENIA NA
ŚCINANIE
tef
max 2 a1
bs hs
2 bs hs
+
(
)
,
0.15 m
=
:=
Ak
bs tef
-
(
)
hs tef
-
(
)
2.025
10
3
cm
2
=
:=
uk
2 bs tef
-
hs
+
tef
-
(
)
1.8 m
=
:=
TRd.c
2 Ak
tef
fctd
86.786 kN m
=
:=
TRd.c TEd
<
0
=
NIE POTRZEBA ZBROJENIA NA
SKRĘCANIE
TEd
TRd.max
VEd
VRd.max
+
0.152
=
<
1
WARUN EK SP EŁNIONY
Sprawdzenie warunków na m inim alny stopień zbrojenia oraz warunków konstrukcyjnych:
s1 10 cm
=
jak dla I kom binacji
ρw
2Asw
s1 bs
0.168 %
=
:=
ρw.min
0.08
fck MPa
1
-
fyk MPa
1
-
0.088 %
=
:=
ρw ρw.min
>
1
=
smax
min 0.75 dx
bs
,
uk
8
,
22.5 cm
=
:=
s1 smax
<
1
=
WARUN EK SP EŁNIONY
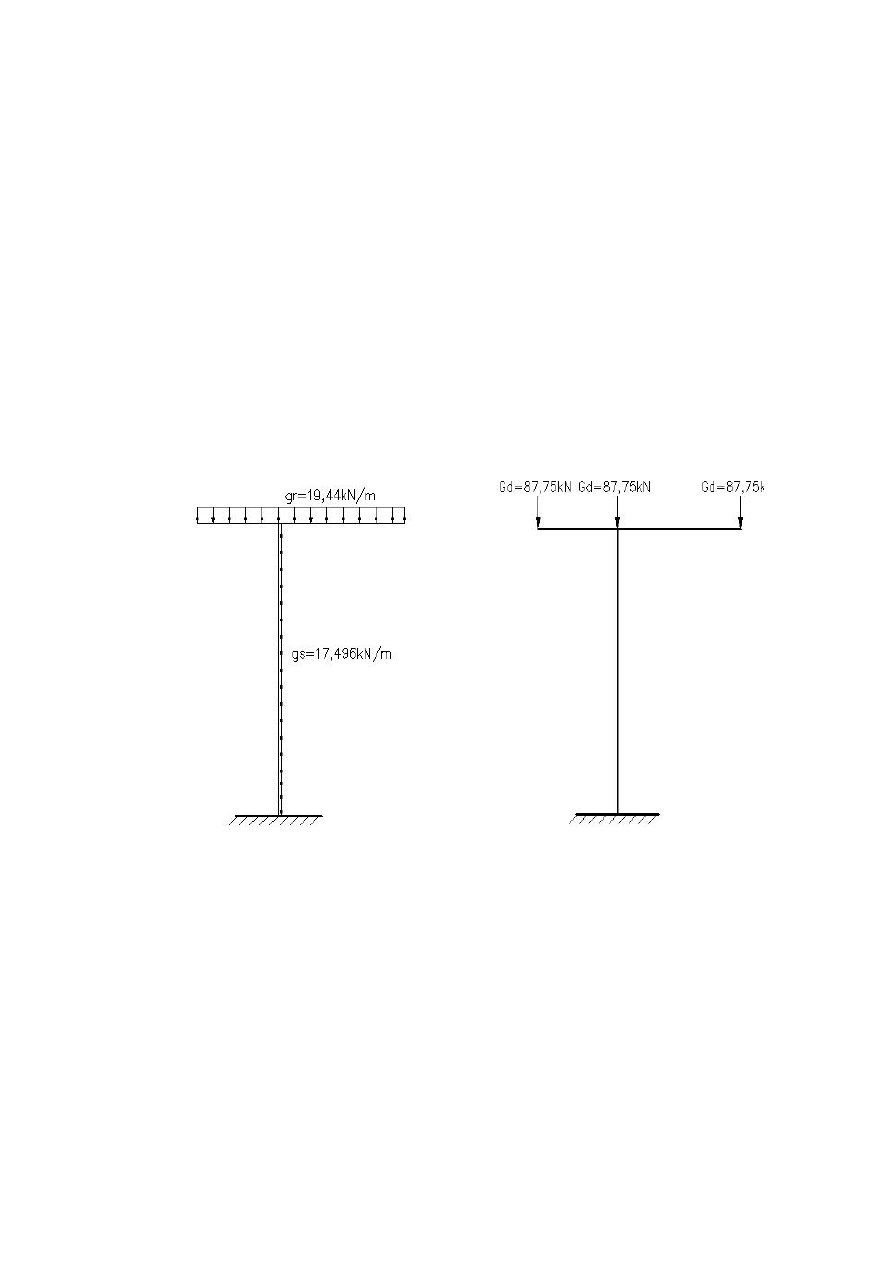
4. Przypadki obciążenia
4.1 Obciążenie stałe (ciężar podpory)
4.2 Obciążenie stałe (ciężar rurociągu)





moc zbrojenia (pole przekroju zbrojenia podłużnego)


tutaj cos






4.2 Obciążenie stałe (ciężar rurociągu)
Wyszukiwarka
Podobne podstrony:
CAŁOSC OD W6 DO W10, podstawy woiągów i kanalizacji
Test wolanin 2011, 7 sem od Jacka, Dla Kamila, VII SEMESTR, do druku wolanin
zoonozy od M zoonozy referat do druku
projekt do druku!
PPM Podstawy Projektowania Maszyn Dziedzic Calów Do druku PPM 04 Koło zębate A3
projekt działki do druku
od pomyslu do realizacji projektu wyklad
do druku PKM., Obliczenia projektowe zasuwa Dn80 "FALI"
projekt wstepny do linii wplywu do druku
Projekt do druku plan
PPM Podstawy Projektowania Maszyn Dziedzic Calów Do druku, PPM 05 Spis Części A3
do druku projekt z?yty
PROJEKT Z ERGONOMII SPAWACZ DO DRUKU
moje, IŚ Tokarzewski 27.06.2016, V semestr COWiG, PKM (Podstawy konstrukcji mechanicznych), PKM XYZ,
od michała j, Inżynieria środowiska, Podstawy Projektowania Stacji Uzdatniania Wody
Projekt 1 karta projektowa do druku id 39
projekcyjne, Testy psychologiczne, materialy do druku
PPM Podstawy Projektowania Maszyn Dziedzic Calów Do druku, PPM 06 Obliczenia Programowe A4
więcej podobnych podstron