Ekonometria I
Ćwiczenia 1
Ćwiczenia 1
Modele przepływów międzygałęziowych. Działania na macierzach.
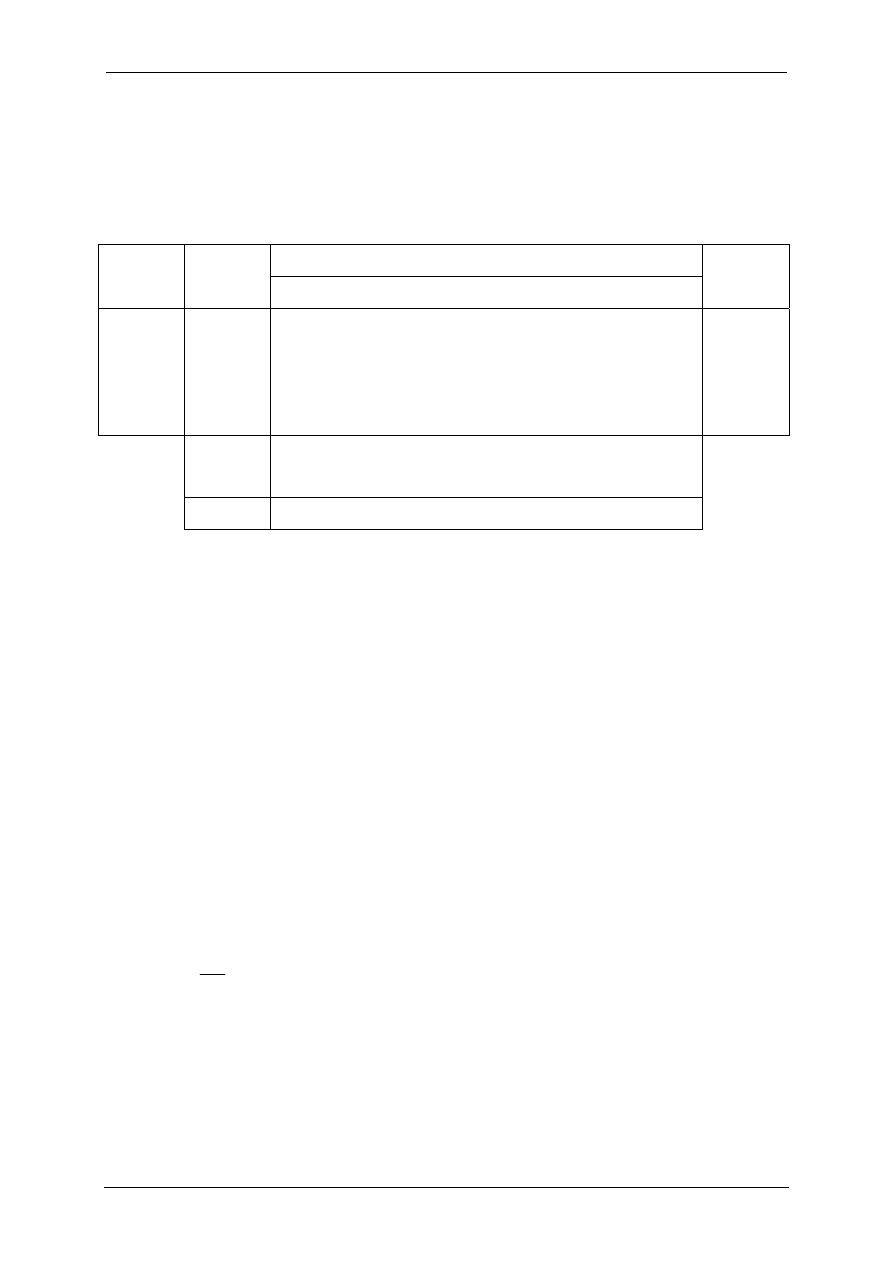
TABLICA PRZEPŁYWÓW MIĘDZYGAŁĘZIOWYCH
x
ij
i X
i
1 2 3 … n
Y
i
1 X
1
x
11
x
12
x
13
… x
1n
Y
1
2 X
2
x
21
x
22
x
23
… x
2n
Y
2
M
M
… M
n X
n
x
n1
x
n2
x
n3
… x
nn
Y
n
x
0j
x
01
x
02
x
03
… x
0n
Z
j
Z
1
Z
2
Z
3
… Z
n
X
j
X
1
X
2
X
3
… X
n
X
i
-
wartość produktu globalnego i-tej gałęzi;
i = 1, 2, …,n
x
ij
-
przepływ z gałęzi i do j, czyli wartość produktu wytworzonego w gałęzi i-tej,
a zużytego przez gałąź j-tą;
j = 1, 2, …,n
Y
i
-
wartość produktu końcowego gałęzi i-tej;
x
0j
-
płace gałęzi j-tej;
Z
j
- zysk gałęzi j-tej.
MODEL LEONTIEFA
Relacje pomiędzy nakładami a wynikami produkcji zwane są relacjami input – output.
W modelu Leontiefa zakłada się, że są one stałe w czasie.
Dla j-tej gałęzi oblicza się współczynniki kosztów:
n
j
X
x
a
j
ij
ij
,...,
1
i,
,
=
=
zwane też współczynnikami bezpośredniej materiałochłonności.
ij
a
- oznacza wartość produktu pochodzącego z gałęzi i-tej, a zużywanego w gałęzi j-tej
w celu wytworzenia w tej gałęzi produktu o wartości jednostkowej.
1
Ekonometria I
Ćwiczenia 1
Współczynniki kosztów
tworzą macierz
ij
a
[ ]
n
n
ij
a
A
×
=
zwaną macierzą struktury kosztów.
Elementy tej macierzy są nieujemne, suma elementów tworzących j-tą kolumnę jest równa
współczynnikowi materiałochłonności m
j
.
Model Leontiefa ma postać:
Y
X
A
I
=
− )
(
X
- n-wymiarowy kolumnowy wektor produktu globalnego;
Y
- n-wymiarowy kolumnowy wektor produktu końcowego.
Macierz Leontiefa ma postać:
A
I
−
Model Leontiefa służy do prognozowania lub symulacji wektora produktu końcowego przy
ustalonej wartości wektora produktu globalnego.
Macierz
A
I
−
jest nieosobliwa, a macierz
ma elementy nieujemne, jeśli suma
elementów każdej kolumny macierz A jest mniejsza od 1.
1
)
(
−
− A
I
Znając powyższe własności macierzy można dokonać przekształcenia:
Y
X
A
I
=
− )
(
Y
A
I
X
A
I
A
I
1
1
)
(
)
(
)
(
−
−
−
=
−
−
Y
A
I
X
1
)
(
−
−
=
Elementy macierzy
noszą nazwę współczynników pełnej materiałochłonności.
1
)
(
−
− A
I
Zadanie 1
Dana jest tablica przepływów międzygałęziowych postaci:
i X
i
x
ij
Y
i
1 500 50 195 0 255
2 300 100 0 90 110
3 150 80 45 15 10
x
0j
200 30 15
Z
j
70 30 30
X
j
500 300 150
2
Ekonometria I
Ćwiczenia 1
a) Obliczyć współczynniki kosztów.
b) Zapisać macierz struktury kosztów. Zinterpretować elementy drugiej kolumny
utworzonej macierzy.
c) Zapisać macierz Leontiefa.
d) Obliczyć wektor produktu końcowego, na podstawie modelu Leontiefa, wykorzystując
dany wektor produktu globalnego.
e) Wyznaczyć macierz odwrotną do macierzy Leontiefa.
f) Wykorzystując macierz odwrotną do macierzy Leontiefa oraz wektor produktu
końcowego, wyznaczyć wektor produktu globalnego.
Zadanie 2
Dana jest tablica przepływów międzygałęziowych trzygałęziowego układu gospodarczego:
Produkt globalny
Przepływy
Produkt
końcowy
200 40 50 36 74
250 50 75 36 89
180 20 45 72 43
a) Wyznaczyć macierz struktury kosztów A oraz podać interpretację wyrazów drugiego
wiersza tej macierzy.
b) Wyznaczyć macierz I-A i sprawdzić, która z podanych macierzy jest macierzą do niej
odwrotną:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
81
,
1
65
,
0
24
,
0
38
,
0
83
,
1
22
,
0
73
,
0
69
,
0
15
,
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
04
,
2
66
,
0
46
,
0
84
,
0
84
,
1
68
,
0
72
,
0
62
,
0
53
,
1
Zadanie 3
Dane są macierze:
3
1 2
1
2 3
2 0
2 0
1 0 3 ,
4
0 1 ,
0 1 ,
1 1
4
2 1
1 2 2
1 1
⎡
⎤
⎡
⎤
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
= −
=
=
= ⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
⎢
⎥
−
⎣
⎦
⎣
⎦
⎣
⎦
A
B
C
D
Wyznaczyć:
a)
b)
T
C
(2
)
−
A
B C
c)
2
D
3
Ekonometria I
Ćwiczenia 1
Zadanie 4
Wykonać działania:
a)
b)
[
]
c)
2
1 0
2 1
⎡
⎤
⎢
⎥
⎣
⎦
1
2
1 2 3 4
3
4
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎣ ⎦
1
0
1
2 1
2
1
3
2
0
1 5
⎡
⎤
−
⎡
⎤ ⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦ ⎢
⎥
−
⎣
⎦
d)
8
1
1 6
2
7
5 2
6
3
3 4
0
0
T
⎡
⎤
⎡
⎤ ⎢
⎥
−
⎢
⎥ ⎢
⎥
⋅
⎢
⎥ ⎢
⎥
−
⎢
⎥ ⎢
⎥
⎣
⎦
⎣
⎦
Zadanie 5
Jeżeli to możliwe, obliczyć:
a)
b) c)
⋅ + ⋅
A C B C
T
+
A C
T
T
T
+
⋅
A B
C
A
d)
(
)
T
⋅
A B
,
gdy:
i
2
1 0
1
1
5
0
1
3
−
⎡
⎤
⎢
⎥
= ⎢
⎥
⎢
⎥
⎣
⎦
A
1 1
0
1 0
5
0
1
2
−
⎡
⎤
⎢
⎥
= −
−
⎢
⎥
⎢
⎥
−
−
⎣
⎦
B
oraz
1 3
2 2
3 1
⎡
⎤
⎢
⎥
= ⎢
⎥
⎢
⎥
⎣
⎦
C
Zadanie 6
Znaleźć wartości wyznaczników:
a)
0 3
1 1
b)
2sin
2cos
-cos
sin
x
x
x
x
c)
3 0 1
2 0 1
0 1 1
d)
0
0
0
1
1
1
5
1 4
−
e)
7
2
1
0
3
5
7
1
6
−
−
−
Zadanie 7
Znaleźć macierz odwrotną do macierzy:
a)
b)
c)
3 1
0 2
⎡
⎤
⎢
⎥
⎣
⎦
2 1
1
5 2
4
7 3
2
−
⎡
⎤
⎢
⎢
⎢
⎥
⎣
⎦
⎥
⎥
2 7 3
3 9 4
1 5 3
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
d)
1 2 1
1 4 2
1 3 2
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
e)
1 2 3
0 1 2
2 1 1
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Zadanie 8
Dla poniższych danych sprawdzić, czy prawdziwa jest równość
1
−
=
⋅
X
A
B
:
1
1
1
1
0 ,
1 1
1 ,
0
1
1
1
1
−
⎡ ⎤
⎡
⎤
⎡ ⎤
⎢ ⎥
⎢
⎥
⎢ ⎥
=
= −
−
=
⎢ ⎥
⎢
⎥
⎢ ⎥
⎢ ⎥
⎢
⎥
⎢ ⎥
0
2
−
−
−
⎣ ⎦
⎣
⎦
⎣ ⎦
X
A
B
Zadanie 8
Sprawdzić, czy
(
)
, jeżeli
T
T
⋅
=
⋅
A B
B
A
T
1 1 3
3 2 1
,
2 2 1
2 1 1
3 2 1
⎡
⎤
⎡
⎤
⎢
⎥
=
=
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎣
⎦
A
B
4