Obraz w układzie bliskich

soczewek

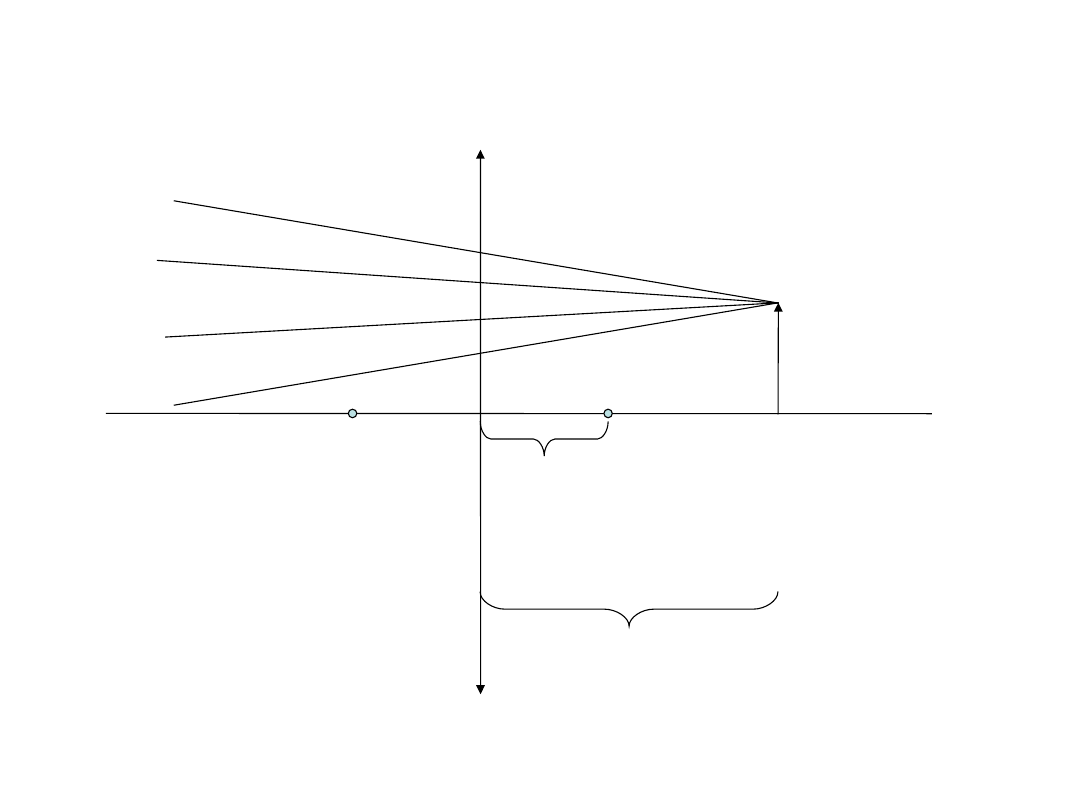
Zadanie 1

W zbieżną wiązkę promieni, które tworzą obraz rzeczywisty, wstawiono soczewkę o
ogniskowej f=3cm w odległości 7 cm od punktu skupienia. W jakiej odległości od soczewki
powstanie nowy obraz?

7cm

3cm

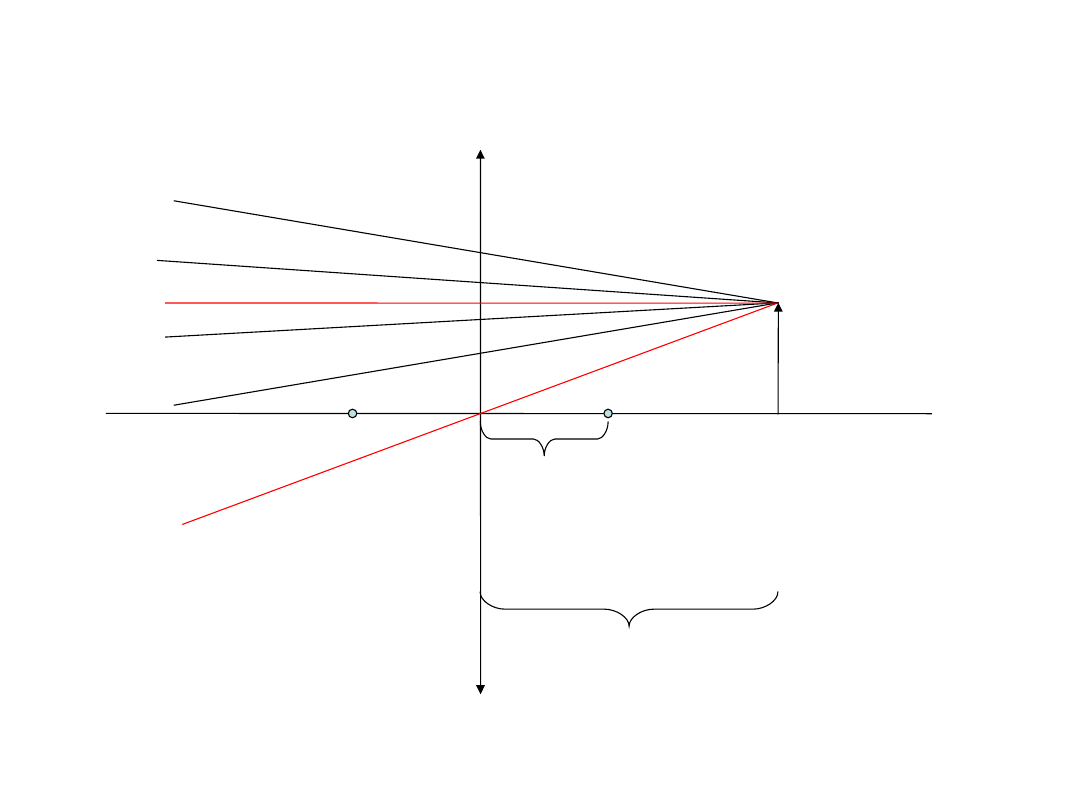
Zadanie 1

W zbieżną wiązkę promieni, które tworzą obraz rzeczywisty, wstawiono soczewkę o
ogniskowej f=3cm w odległości 7 cm od punktu skupienia. W jakiej odległości od soczewki
powstanie nowy obraz?

7cm

3cm

Pomogą nam promienie
charakterystyczne.

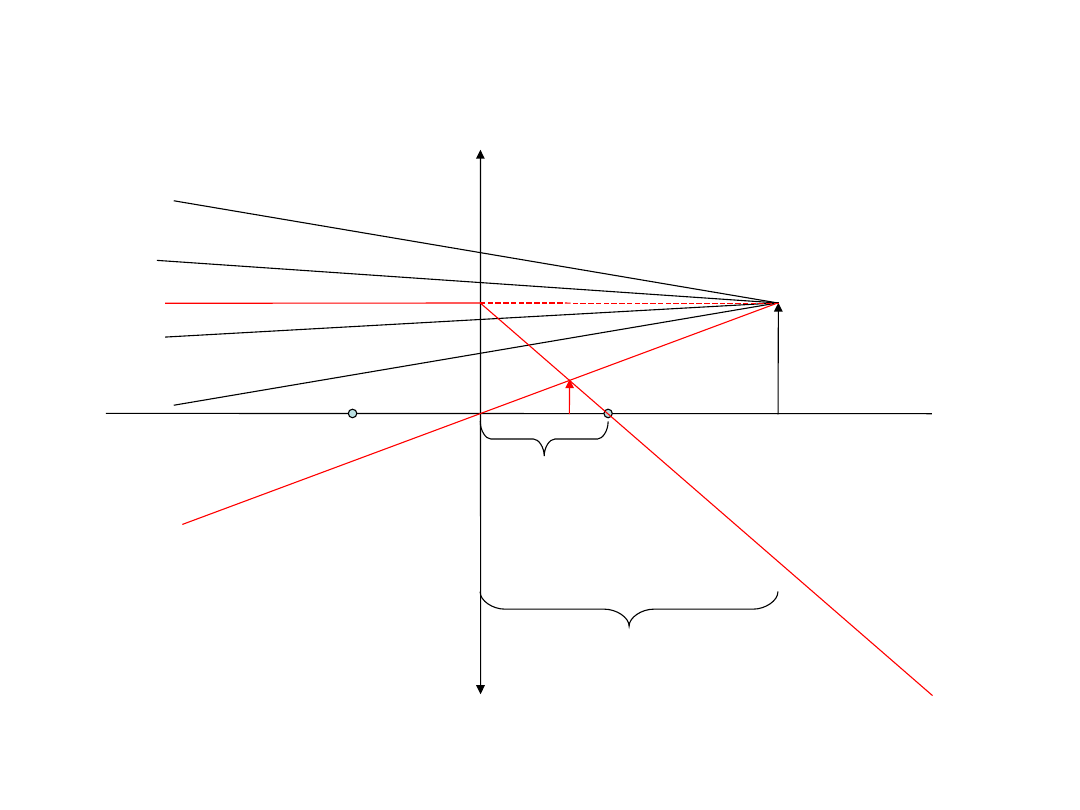
Zadanie 1

W zbieżną wiązkę promieni, które tworzą obraz rzeczywisty, wstawiono soczewkę o
ogniskowej f=3cm w odległości 7 cm od punktu skupienia. W jakiej odległości od soczewki
powstanie nowy obraz?

7cm

3cm

Sukces! Ale jak obliczyć położenie nowego punktu skupienia?

Zauważmy, że bieg promieni jest taki sam jak w lupie.

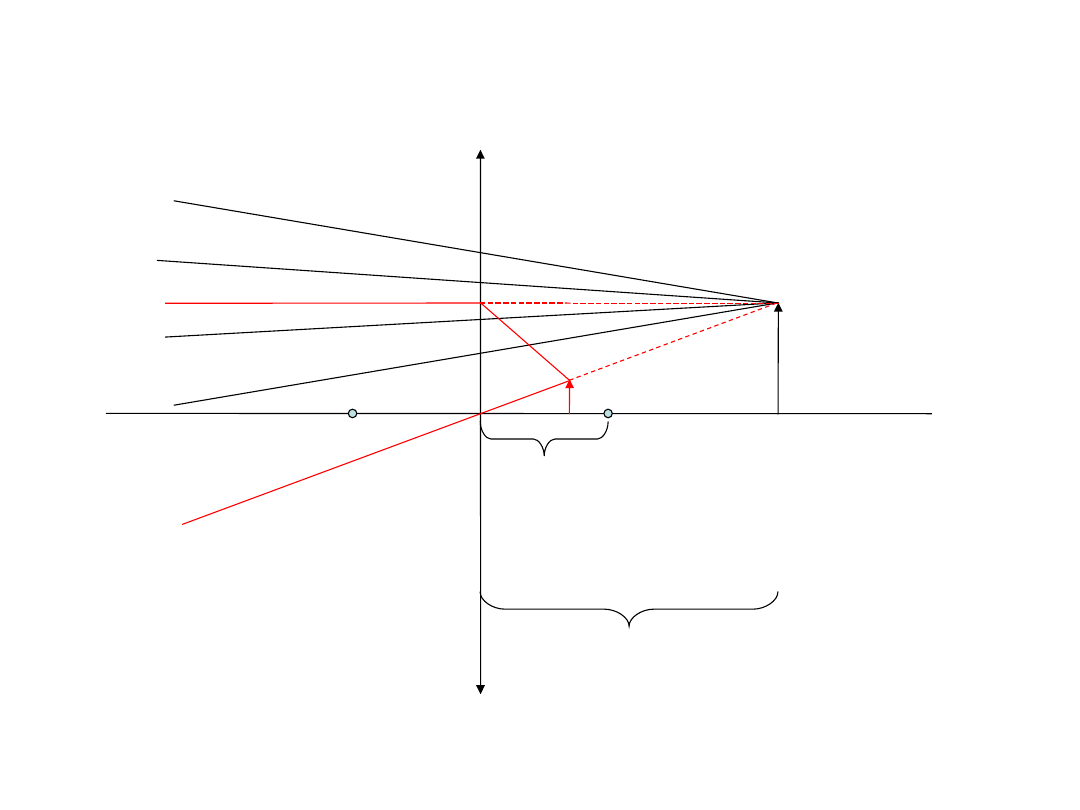
Zadanie 1

W zbieżną wiązkę promieni, które tworzą obraz rzeczywisty, wstawiono soczewkę o
ogniskowej f=3cm w odległości 7 cm od punktu skupienia. W jakiej odległości od soczewki
powstanie nowy obraz?

7cm

3cm

Możemy zastosować równanie soczewki, w którym x jest nieznane, f=3, y=-7. Wynik to x=2,1.
Przy okazji widzimy, że gdy wstawiamy soczewkę w zbieżną wiązkę promieni, odległość między
soczewką a pierwotnym punktem skupienia musi być w równaniu użyta z minusem. Ten punkt
pełni zawsze rolę pozornego obrazu.

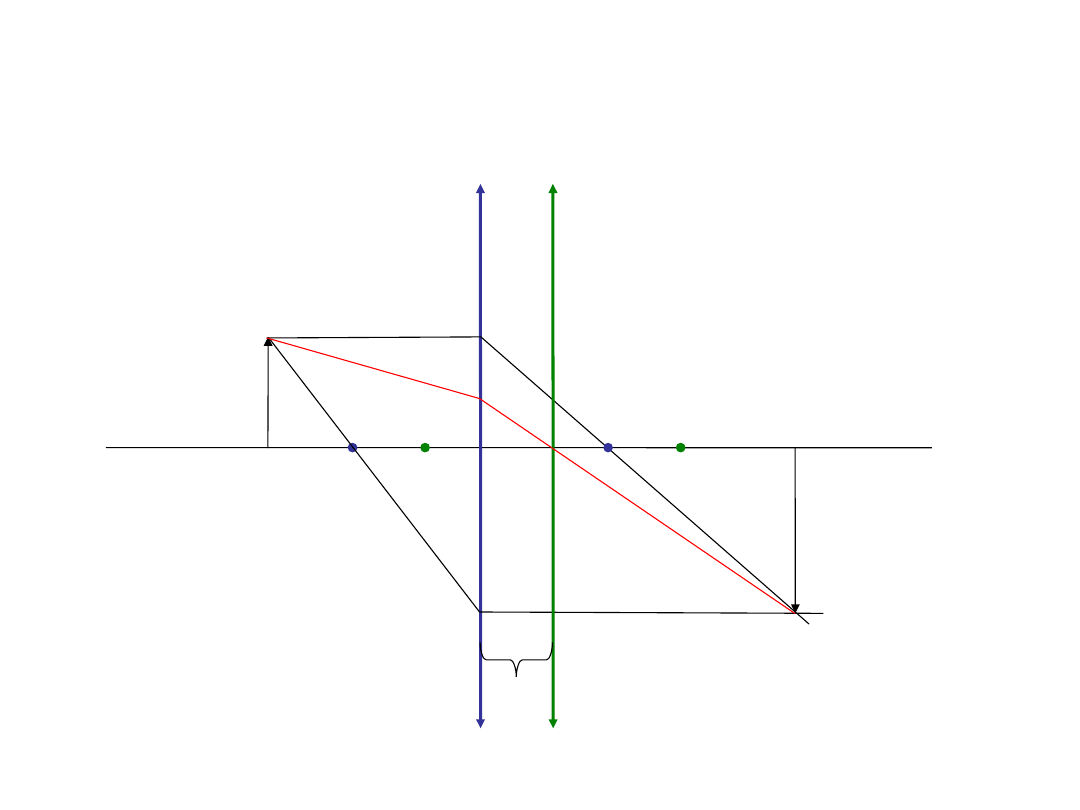
Zadanie 2

Znajdź położenie obrazu, gdy światło przechodzi przez dwie blisko siebie leżące soczewki
skupiające o ogniskowych f

1

, f

2

. Odległość między soczewkami wynosi a. Soczewki leżą tak

blisko siebie, że promienie idące przez pierwszą soczewkę trafiają do drugiej nim utworzą
obraz.

a

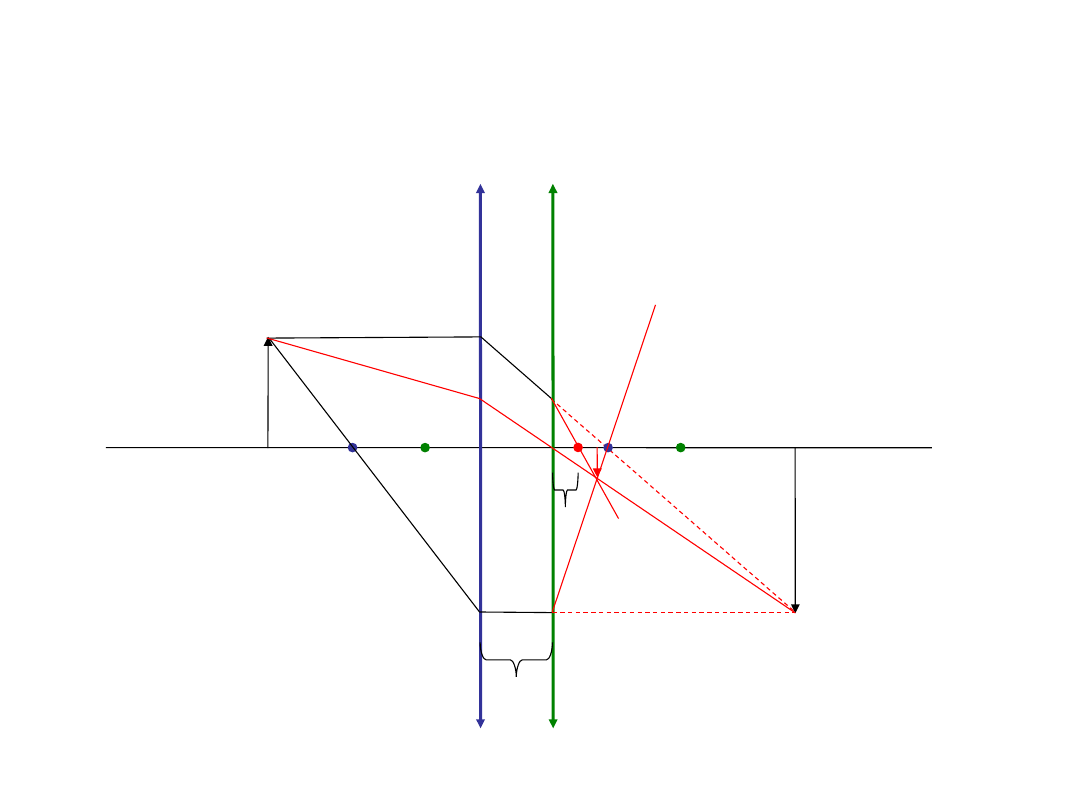
Zadanie 2

Znajdź położenie obrazu, gdy światło przechodzi przez dwie blisko siebie leżące soczewki
skupiające o ogniskowych f

1

, f

2

. Odległość między soczewkami wynosi a. Soczewki leżą tak

blisko siebie, że promienie idące przez pierwszą soczewkę trafiają do drugiej nim utworzą
obraz.

a

f

Zadanie 3

Oblicz położenie obrazu gdy f

1

=f

2

=1, x=2, a=1/2.

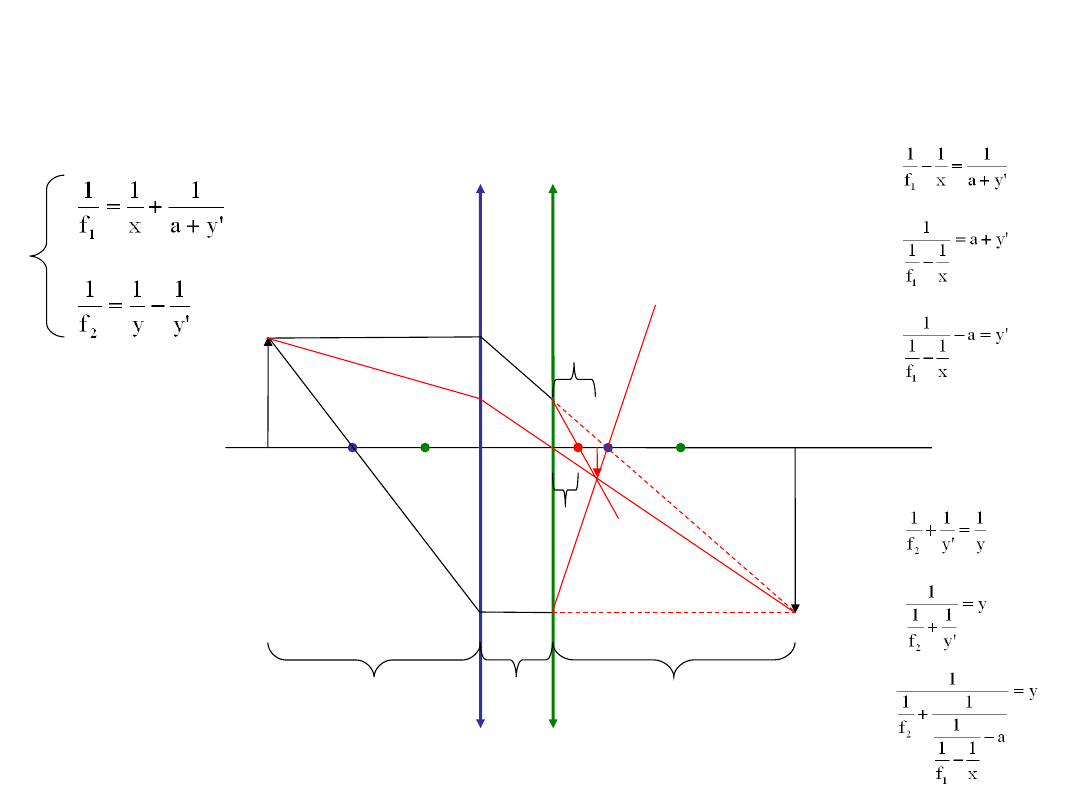
a

f

y’

y

x

W drugim
równaniu
uwzględniliśmy,
że odległość y’
trzeba wstawić z
minusem.

Wprowadźmy kilka oznaczeń, by zapisać równanie dla każdej z soczewek.

Odp: y=3/5

Radzimy
rozwiązywać ten
układ na liczbach. W
rozwiązaniu na
samych literach
łatwo o pomyłkę,
zwłaszcza gdy ktoś
próbuje usuwać
ułamki piętrowe.
Rozwiązanie na
literach jest do
prześledzenia obok .

Z pierwszego
równania
wyznaczamy y’.

Z drugiego równania
otrzymujemy:

Po podstawieniu y’ z
pierwszego równania
otrzymujemy:

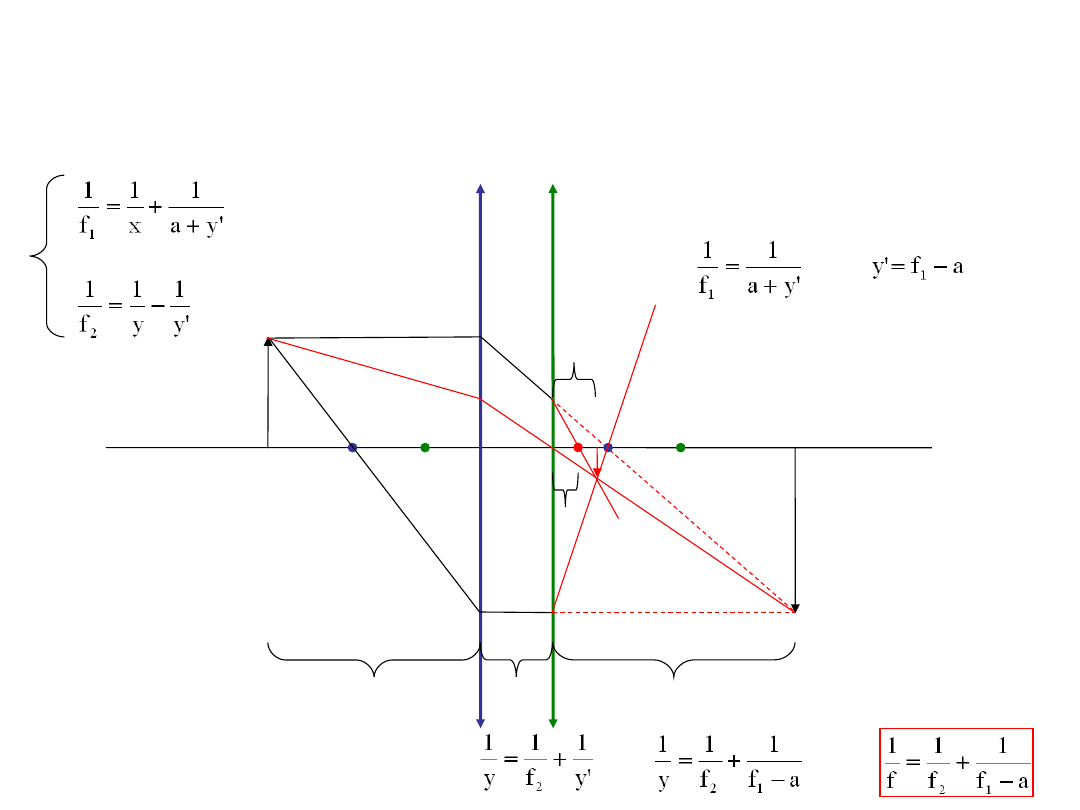
Zadanie 4

Jaki jest związek ogniskowej sumarycznej z ogniskowymi soczewek składowych?

a

f

y’

y

x

Startujemy ze znanego nam układu równań:

Aby obraz znalazł się w ognisku
przedmiot musi być w nieskończoności.
Wtedy z pierwszego równania
dostajemy:

Z drugiego wyliczamy 1/y i
wstawiamy y’ z pierwszego. W końcu
uwzględniamy, że w założonej
sytuacji y=f:

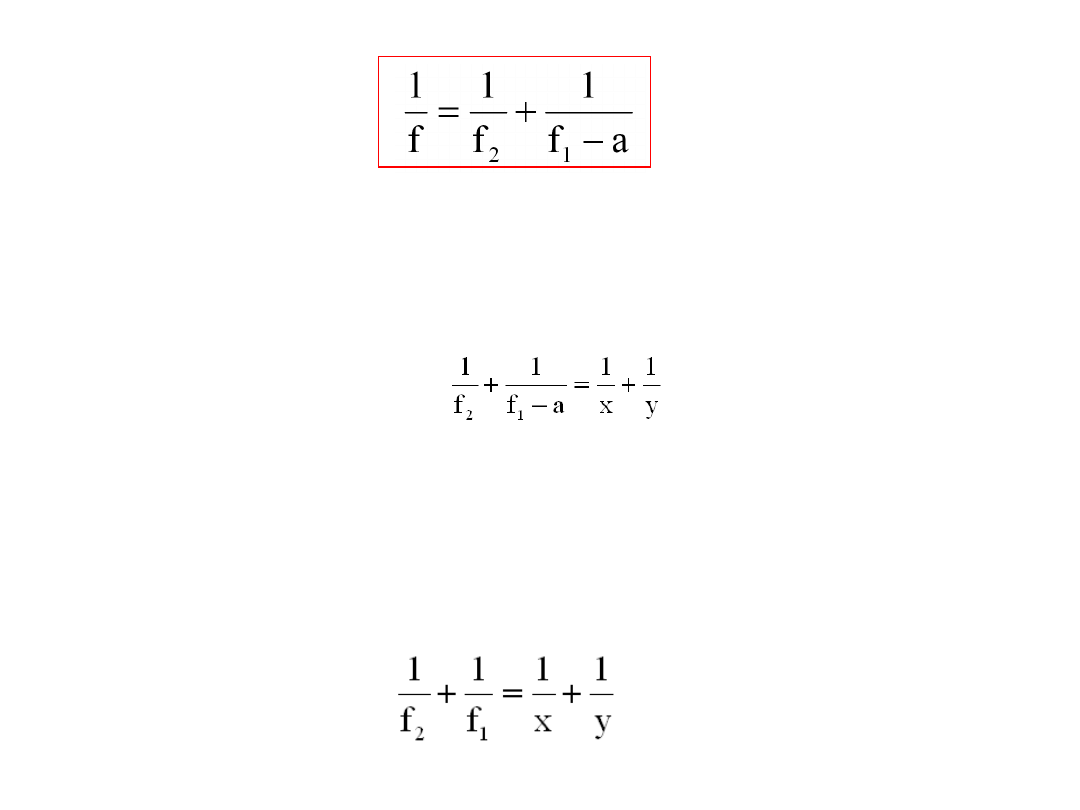
Jednak takiej ogniskowej nie możemy wstawiać do równania soczewki. Układ soczewek nie
działa jak jedna soczewka.

Zadanie 5.

Wykaż, że założenie słuszności wzoru prowadzi do błędnego
wyniku.

W tym celu oblicz położenie obrazu, gdy f

1

=f

2

=1, x=2, a=1/2 .

Odpowiedź: y=2/5.

Zadanie 6

Za pomocą znanego nam układu równań wykaż, że gdy soczewki są nieskończenie blisko
siebie, słuszne jest równanie:

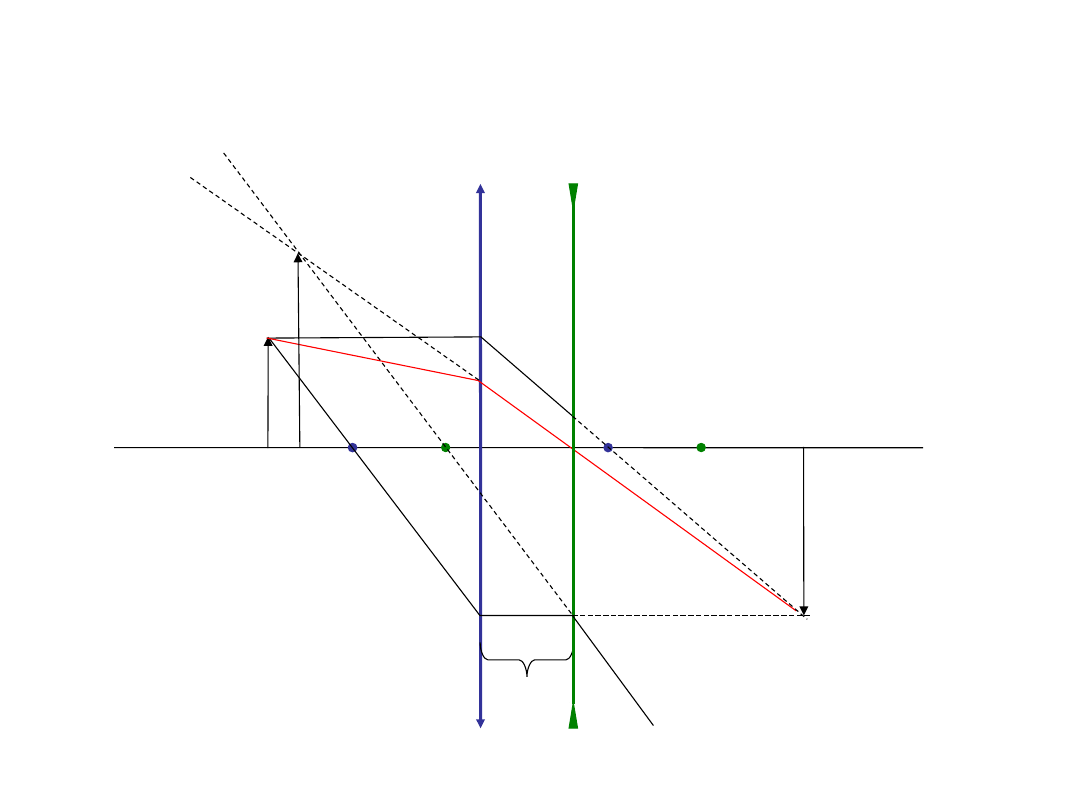
Zadanie 7

Znajdź graficznie położenie obrazu, gdy światło przechodzi przez dwie blisko siebie leżące
soczewki - najpierw skupiającą, potem rozpraszającą o przeciwnej mocy.

a

Zadziałały jak soczewka rozpraszająca, bo obraz jest pozorny, ale jednocześnie jak lupa, bo jest
powiększony.

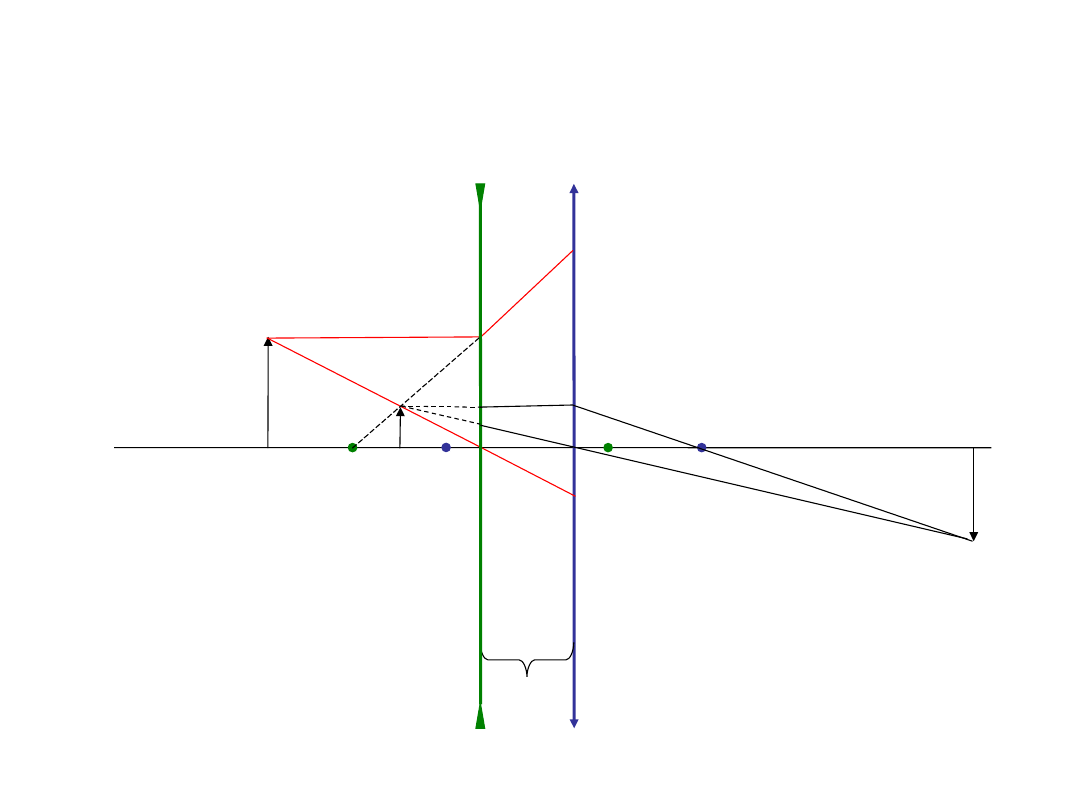
Zadanie 8

Zamieniliśmy soczewki miejscami. Znajdź graficznie położenie obrazu, gdy światło
przechodzi przez dwie blisko siebie leżące soczewki najpierw rozpraszającą, potem
skupiającą o przeciwnej mocy.

a

Zadziałały jak soczewka skupiająca.

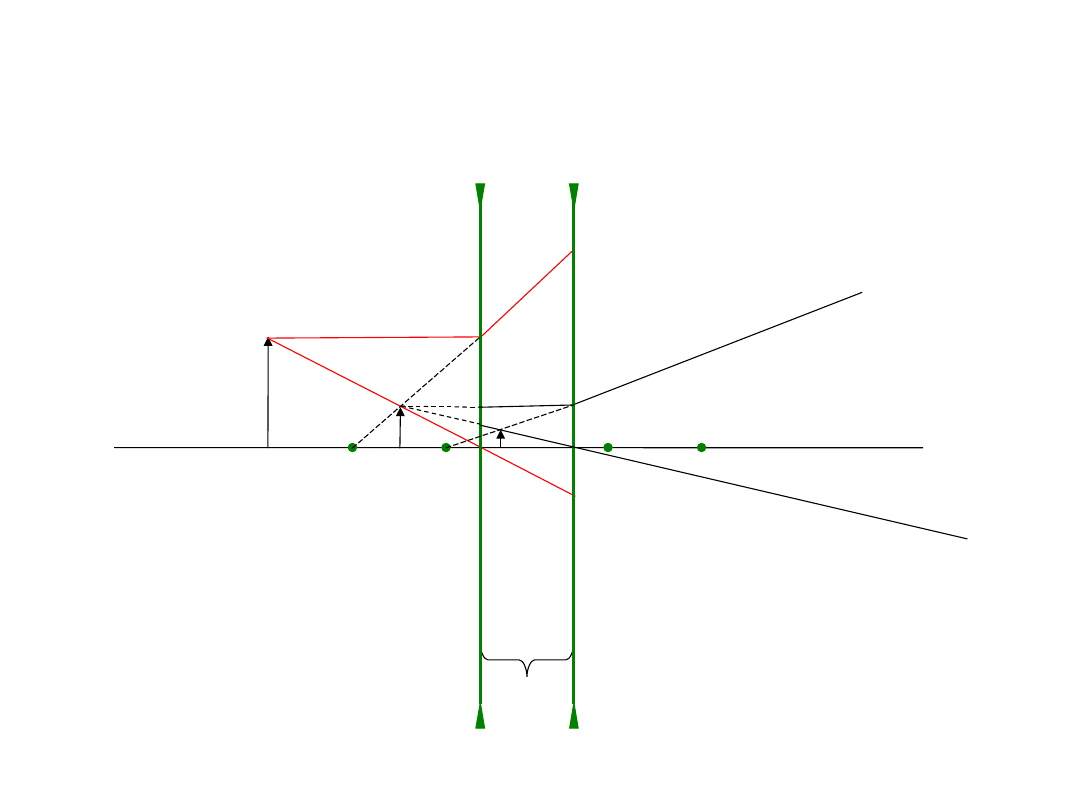
Zadanie 9

Znajdź graficznie położenie obrazu, gdy światło przechodzi przez dwie
blisko siebie leżące soczewki rozpraszające.

a

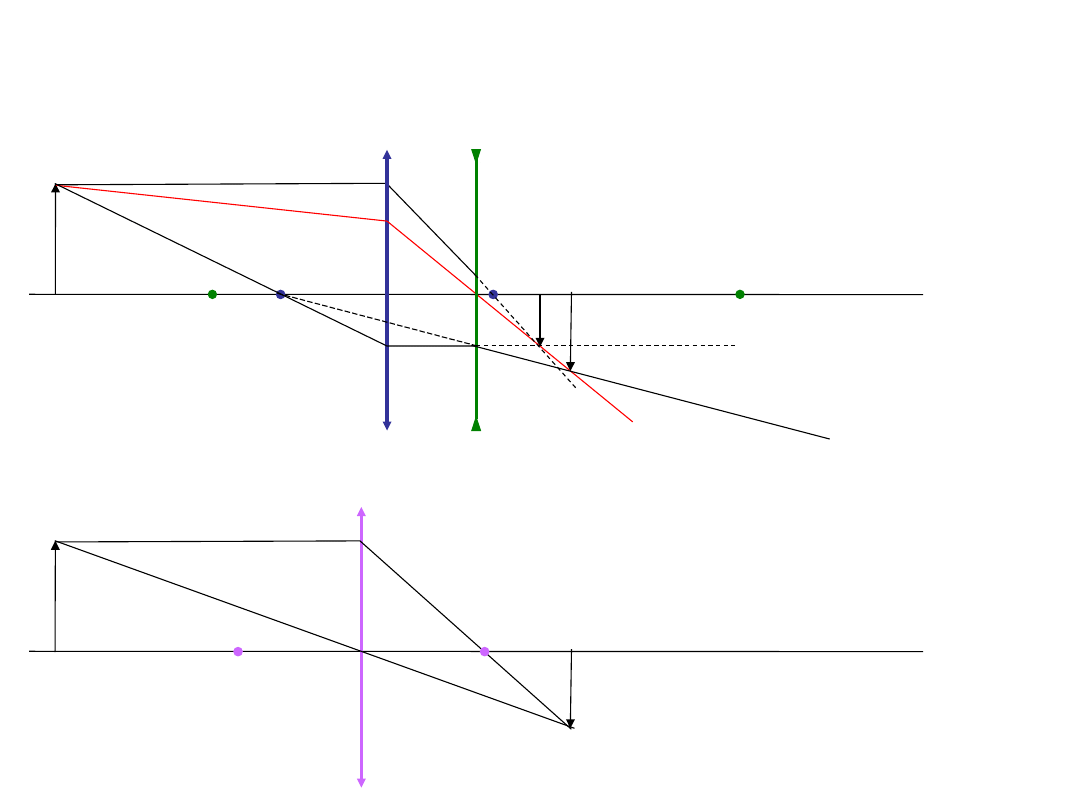
Zadanie 7

Znajdź graficznie położenie obrazu, gdy światło przechodzi przez dwie blisko siebie leżące
soczewki - najpierw skupiającą, potem dużo słabszą rozpraszającą.

Tak użyta soczewka rozpraszająca, tzw.
soczewka Barlowa, pozwala skrócić długość
obiektywu w stosunku do obiektywu z jednej
soczewki, dającego to samo powiększenie.

Zadanie 8

Udowodnij poprzednie stwierdzenie. Znajdź graficznie położenie i ogniskową soczewki
pojedynczej, która daje to samo powiększenie z tej samej odległości.

Porównajmy soczewki skupiające.

Prezentację wykonał

Wiesław Kruczała

styczeń 2019