Rodzaje algorytmów
i
sposoby ich
prezentacji

Wykonała Agnieszka Karczmarczyk 2 inf

Spis treści



Co to algorytm?



Po co nam te algorytmy?

 



Cechy algorytmów



Jak prezentujemy algorytmy?



Jak powstaje algorytm? 



Algorytmy liniowe 



Algorytmy z warunkami



Algorytmy iteracyjne  



Rodzaje bloków



Poprawność algorytmu



Pomysł Euklidesa na obliczanie NWD



Budowa schematu blokowego

Algorytm



Algorytm – w matematyce oraz informatyce to skończony,

uporządkowany ciąg jasno zdefiniowanych czynności,

koniecznych do wykonania pewnego zadania. Słowo

"algorytm" pochodzi od nazwiska Muhammed ibn Musa

Alchwarizmi matematyka perskiego z IX wieku i

początkowo oznaczało w Europie sposób obliczeń oparty na

dziesiętnym systemie liczbowym.



Algorytm ma przeprowadzić system z pewnego stanu

początkowego do pożądanego stanu końcowego. Badaniem

algorytmów zajmuje się algorytmika. Algorytm może

zostać zaimplementowany w postaci programu

komputerowego lub dla innego urządzenia. Kiedy podczas

tego procesu programista popełni błąd, może to

doprowadzić do poważnych konsekwencji np. błędy w

implementacji algorytmów bezpieczeństwa mogą ułatwić

popełnienie przestępstwa komputerowego.

Powró
t

Po co nam te
algorytmy?

 



Algorytmika dostarczyła wiele efektywnych metod

rozwiązywania różnorodnych problemów, które mogą

być użyte w dowolnym języku programowania.



Algorytmy stanowią trzon informatyki. Są głównym

obiektem zainteresowania naukowców i inżynierów 

w wielu dziedzinach techniki.



Głównym celem poznawania zasad prawidłowego

konstruowania i analizowania algorytmów jest to, że

dzięki nim otrzymuje się możliwość ogromnych

oszczędności zasobów.



Prawidłowo skonstruowane algorytmy, oparte na

przemyślanej koncepcji algorytmicznej, są nieraz

miliony razy szybsze od amatorskich, a często jako

jedyne pozwalają na rozwiązanie danego zadania.

Powró
t

Cechy algorytmów



Poprawność



dla poprawnych danych algorytm powinien podawać

prawidłowy wynik.



Skończoność



algorytm musi dać się wykonać w skończonej liczbie

kroków (musi się zakończyć).



Uniwersalność



rozwiązanie danego problemu powinno być możliwe dla

każdego zestawu danych.



Efektywność



algorytm powinien wykonywać swoje zadanie w jak

najkrótszym czasie, wykorzystując przy tym jak

najmniejszą ilość pamięci.



z każdym algorytmem wiąże się miara efektywności, zwana

złożonością obliczeniową, wyrażana liczbą operacji

wykonywanych przez algorytm.

Powró
t

Jak prezentujemy
algorytmy? 



Algorytmy można przedstawiać w różnych postaciach, 

w zależności od problemu, którego dotyczą.



Najczęściej stosowane sposoby zapisu algorytmów:

•

opis słowny - jest to najprostszy i najmniej ścisły sposób

przedstawienia algorytmu,

•

lista kroków - to przedstawienie algorytmu w kolejnych

punktach, w których podaje się wykaz podejmowanych działań

oraz ewentualne warunki przechodzenia do innych kroków.

•

schemat blokowy (zwany także siecią działań) - jest jednym

z najbardziej popularnych graficznych sposobów

przedstawiania algorytmów. W takim schemacie

poszczególnym krokom algorytmu odpowiadają bloki o różnym

kształcie, a kolejność ich wykonywania ilustrują strzałki.

•

drzewo algorytmu - uproszczona odmiana schematu

blokowego

Powró
t

Jak powstaje algorytm?

 



Algorytmy budowane są na podstawie specyfikacji.



Problem algorytmiczny składa się z dwóch elementów:



specyfikacja danych do problemu (określenie jaką postać

mają dane i jakie spełniają założenia)



specyfikacja wyniku jako pewnej funkcji danych.



Przykłady specyfikacji:



Problem: Obliczanie pola powierzchni i objętości

czworościanu  

                    foremnego o boku a. 

Dane: dowolna liczba rzeczywista dodatnia a. 

Wynik: wartość pola P i objętości V.



Problem: Sprawdzanie, czy dany wyraz jest palindromem. 

Dane: dowolny wyraz (ciąg znaków składający się z liter). 

Wynik: określenie „tak”, jeśli wyraz jest palindromem, 

                    „nie” - w przeciwnym przypadku.

Powró
t

Algorytmy liniowe 



W algorytmie liniowym wszystkie kroki
są wykonywane jeden po drugim,
dokładnie w takiej kolejności, w jakiej
występują.



Algorytm liniowy nie może zawierać
konstrukcji warunkowych (czyli
rozgałęzień), ani pętli. Nie jest więc
możliwe ani ominięcie, ani powtórne
wykonanie jakiegoś kroku.

Powró
t

Algorytmy z
warunkami 



W praktyce często spotykamy się z algorytmami, 

w których występują alternatywne warianty działań.

Takie algorytmy nie mogą być liniowe. Nazywamy je

algorytmami z warunkami lub rozgałęzieniami.



W algorytmach z warunkami istnieją konstrukcje

warunkowe. W wyniku sprawdzenia zapisanego w

nich warunku mogą być wykonywane różne kroki

algorytmu.



Przykłady algorytmów z warunkami:



algorytm obliczania wartości bezwzględnej danej liczby

całkowitej,



algorytm wyboru większej z dwóch liczb,



algorytm rozwiązywania równania liniowego a?x+b=0.

Powró
t

Algorytmy iteracyjne

 



W algorytmach iteracyjnych pewien

krok (lub zespół kroków) wykonywany

jest wielokrotnie w pętli, aż do

momentu spełnienia określonego

warunku.



Algorytmy iteracyjne nazywane są

także algorytmami pętlą.



Przykładem algorytmu iteracyjnego jest

sposób obliczania wartości potęg liczb

o wykładnikach naturalnych.

Powró
t

Rodzaje bloków



Bloki graniczne. Mają kształt zaokrąglonego

prostokąta. Wskazują początek i koniec wykonywanego

algorytmu. 



Blok wejścia-wyjścia. Jest równoległobokiem. Oznacza

wprowadzanie danych do programu lub wyprowadzanie

wyników. 



Blok operacyjny. Jest prostokątem, w którym

umieszczone są polecenia lub grupy poleceń

odpowiadające wykonywaniu obliczeń i innych działań na

danych. 



Blok warunkowy. Ma kształt rombu. Oznacza wybór

jednego z dwóch wariantów dalszego wykonywania

programu. 

Powró
t

Poprawność algorytmu



Poprawność semantyczna oznacza, że program

rzeczywiście wykonuje postawione przed nim

zadanie.



Program P jest częściowo poprawny względem

warunku początkowego a i warunku

końcowego b, 

gdy dla dowolnych danych d spełniających a,

jeśli obliczenie programu P zakończy się, to

otrzymany wynik spełnia warunek b.



Program P jest całkowicie poprawny gdy:



jest częściowo poprawny,



dla dowolnych danych d spełniających a obliczenie

programu P zakończy się.

Powró
t

Pomysł Euklidesa na obliczanie
NWD

1. Dane są dwie niezerowe liczby naturalne a i

b.

2. Dopóki liczby nie są równe powtarzaj krok 3,
w przeciwnym razie przejdź do kroku 4.
3. Od większej liczby odejmij mniejszą i tę

większą zastąp otrzymaną różnicą.

4. Wyprowadź wynik: NWD (największy

wspólny dzielnik) jest równy pierwszej
liczbie.

Powró
t

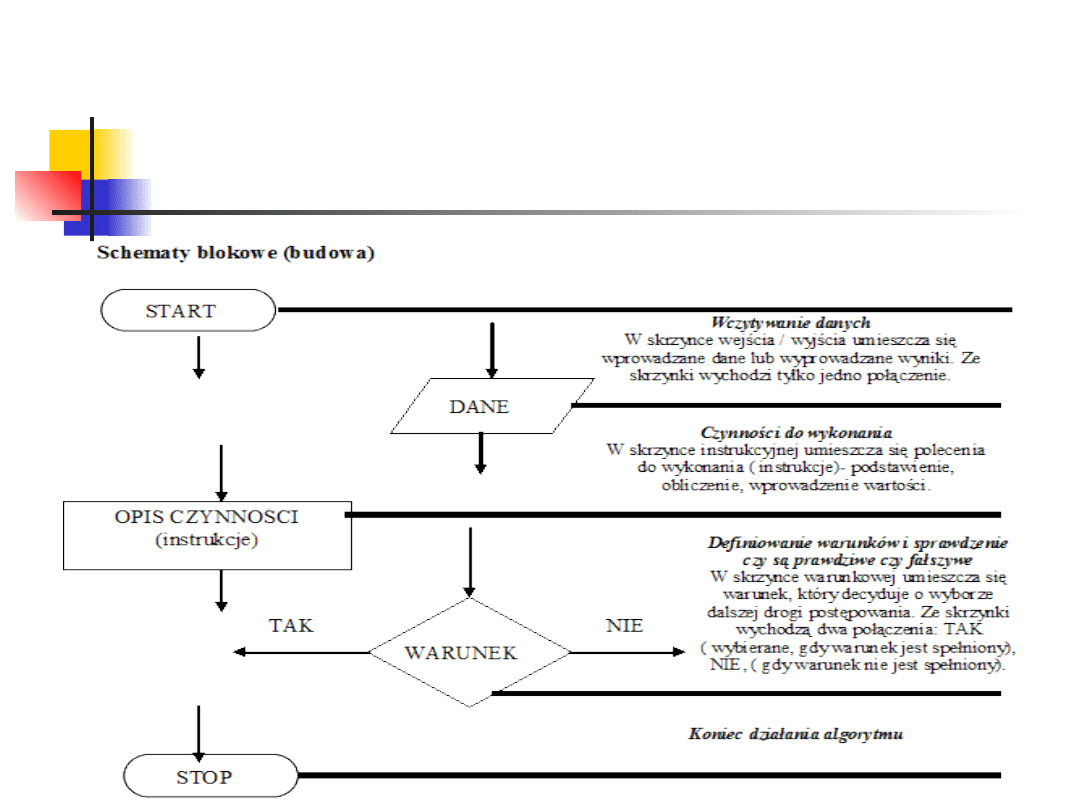
Budowa schematu
blokowego

Powró
t

Koniec

Wykonała Agnieszka Karczmarczyk 2 inf