ANNA BERLIŃSKA – KOMZA
GIMNAZJUM NR 1 W
SIERADZU

Pole jest liczbą, która wyraża ilość kwadratów
jednostkowych mieszczących się w obszarze
danej figury.
Pole tej figury jest równe 12, gdyż w obszarze tej figury
mieści się dwanaście jednakowych kwadratów.

Kwadrat o boku 1 mm i polu równym
1 mm
2
Kwadrat o boku 1 cm i polu
równym 1 cm
2
Kwadrat o boku 1 dm i polu
równym 1 dm
2
itd.
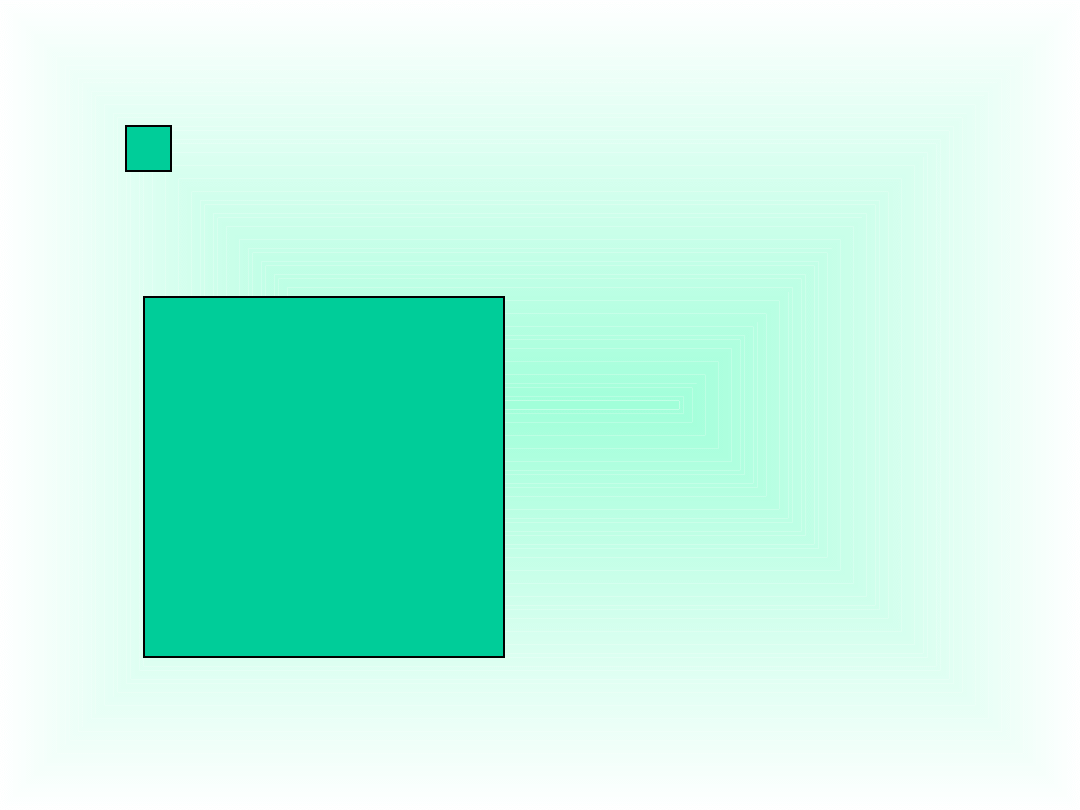
To jest 1 cm2.
To jest 1 dm
.
2
Czy wiesz, że w jednym
decymetrze kwadratowym
mieści się sto centymetrów
kwadratowych!
1 dm = 100 cm
2
2

Jednostki kwadratowe służą do wyrażania pola (powierzchni)
danej figury. Podstawowe jednostki kwadratowe, to:
•jeden milimetr kwadratowy 1mm
•jeden centymetr kwadratowy 1cm
•jeden decymetr kwadratowy 1 dm
•jeden metr kwadratowy 1 m
•jeden kilometr kwadratowy 1 km
2
2
2
2
2

Jeden ar (1a), to pole kwadratu o boku 10 m.
1 a = 100 m
2
Jeden hektar (1ha), to pole kwadratu o boku 100 m.
1 ha =
10000 m
2
1 ha = 100 a

Ile 1 m ma milimetrów kwadratowych ?
2
Jeden metr kwadratowy, to pole kwadratu o boku
jednego metra.
Jeden metr ma sto centymetrów,czyli tysiąc mili-
metrów.
Zatem w 1m mieści się 1000 000 kwadratów
o boku 1 mm.
Możemy więc krótko zapisać zależność:
2
1 m = 1 000 000 mm
2
2
1cm = 100
mm
1m = 10 000
cm
1m = 100 dm
1km = 1 000
000 m
2
2
2
2
2
2
2
2
1mm² = 0,01 cm²
1cm² = 0,0001 m²
1 dm² = 0,01 m²
1 m² = 0,000001km²

• Długość odcinka możemy zmierzyć za pomocą linijki.
• Mało kto wie, że przyrząd do mierzenia pól wynalazł
niemiecki inżynier J. Hermann. Było to w roku 1814 .
Urządzenie nazywa się planimetr.
• Planimetr najczęściej jest używany przez geodetów
do mierzenia powierzchni obszarów na mapach.
PLANIMETRIA –TO NAUKA O FIGURACH
PLANIMETRIA –TO NAUKA O FIGURACH
PŁASKICH
PŁASKICH

a
b
•
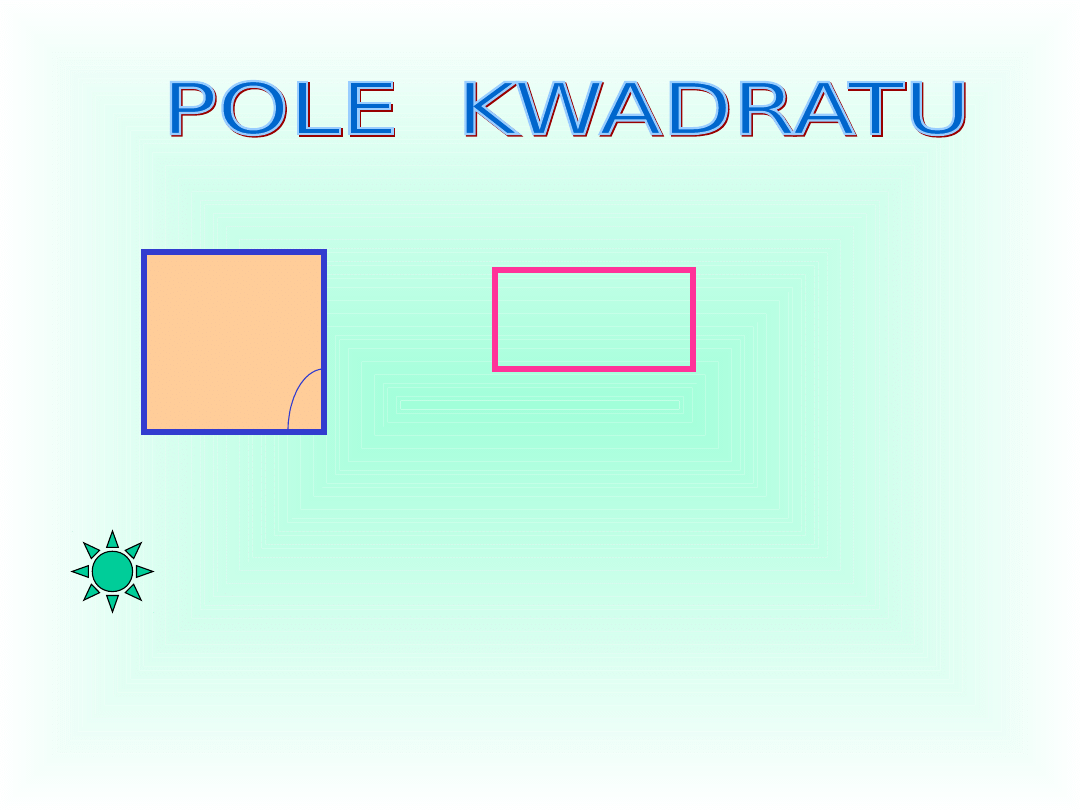
P = a • b
Pole prostokąta jest równe iloczynowi długości
jego dwóch sąsiednich boków.
•
a
a
P = a2
Pole kwadratu jest równe kwadratowi
długości jego boku.

x
x
h
h
a
a
•
a-długość boku
h-długość wysokości opuszczonej na bok a
Pola obu czworokątów są równe. Korzystając
ze wzoru na pole prostokąta, mamy :
P = a•h
Pole równoległoboku jest równe iloczynowi długości
jego boku i wysokości opuszczonej na ten bok.
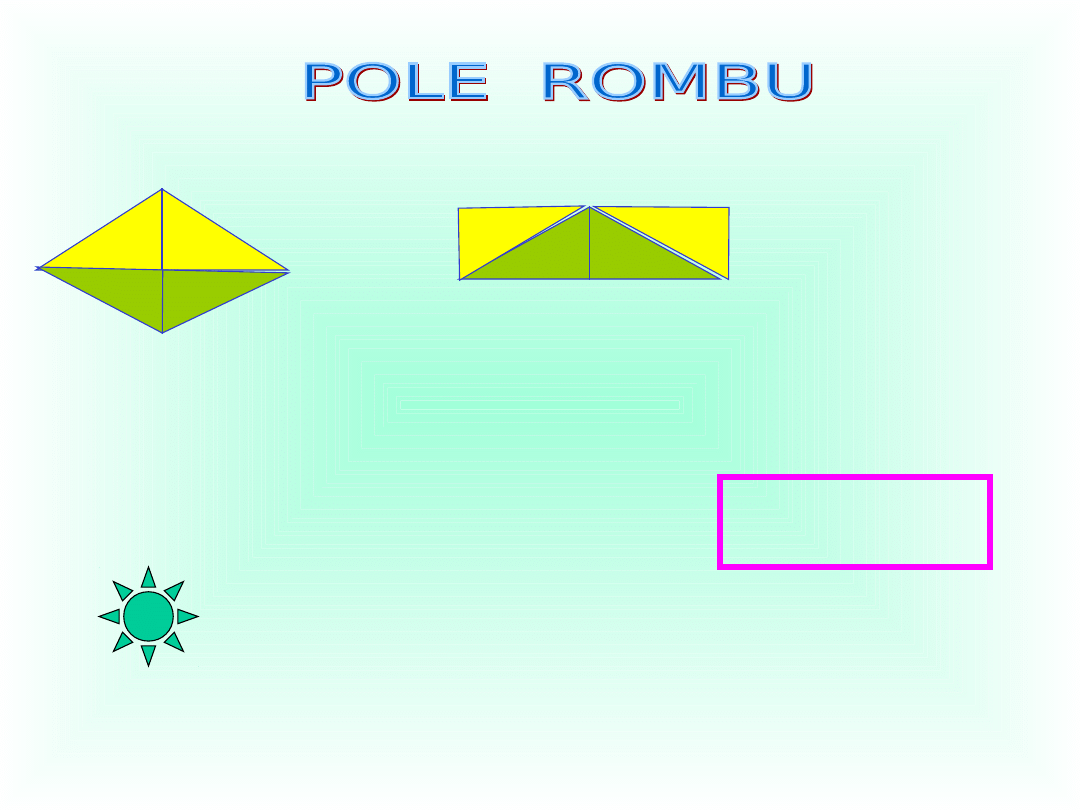
e
½e
f
f
e,f – długości przekątnych rombu
Pola obu czworokątów są równe. Korzystając
ze wzoru na pole prostokąta, mamy:
P = ½ e
• f
Pole rombu jest równe połowie iloczynu
długości obu jego przekątnych.
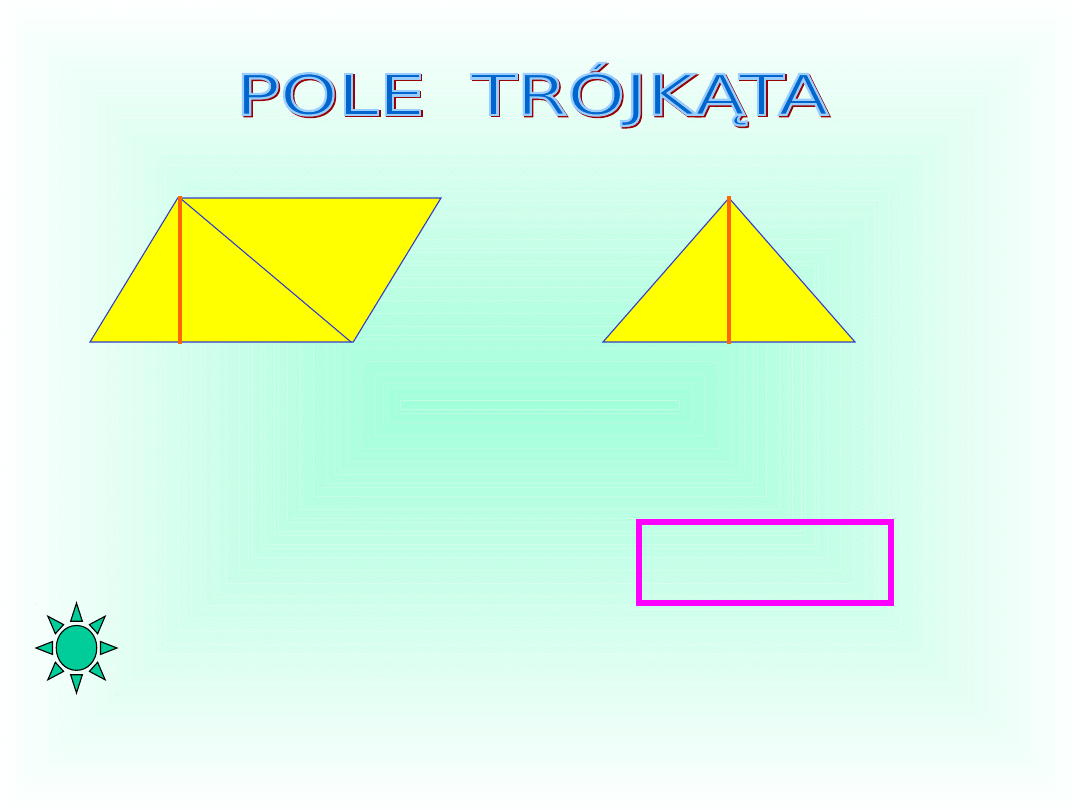
a
a
h
h
Zaobserwuj, że pole trójkąta jest dokładnie równe
połowie pola równoległoboku. Korzystając ze wzoru
na pole równoległoboku mamy:
P = ½ a•h
Pole trójkąta jest równe połowie iloczynu długości
dowolnego boku trójkąta i wysokości opuszczonej
na ten bok.

•
a
b
a i b – boki leżące na
ramionach kąta
prostego, czyli
przyprostokątne
trójkąta
P = ½ a•b
Pole trójkąta prostokątnego równe jest połowie
iloczynu długości jego przyprostokątnych.
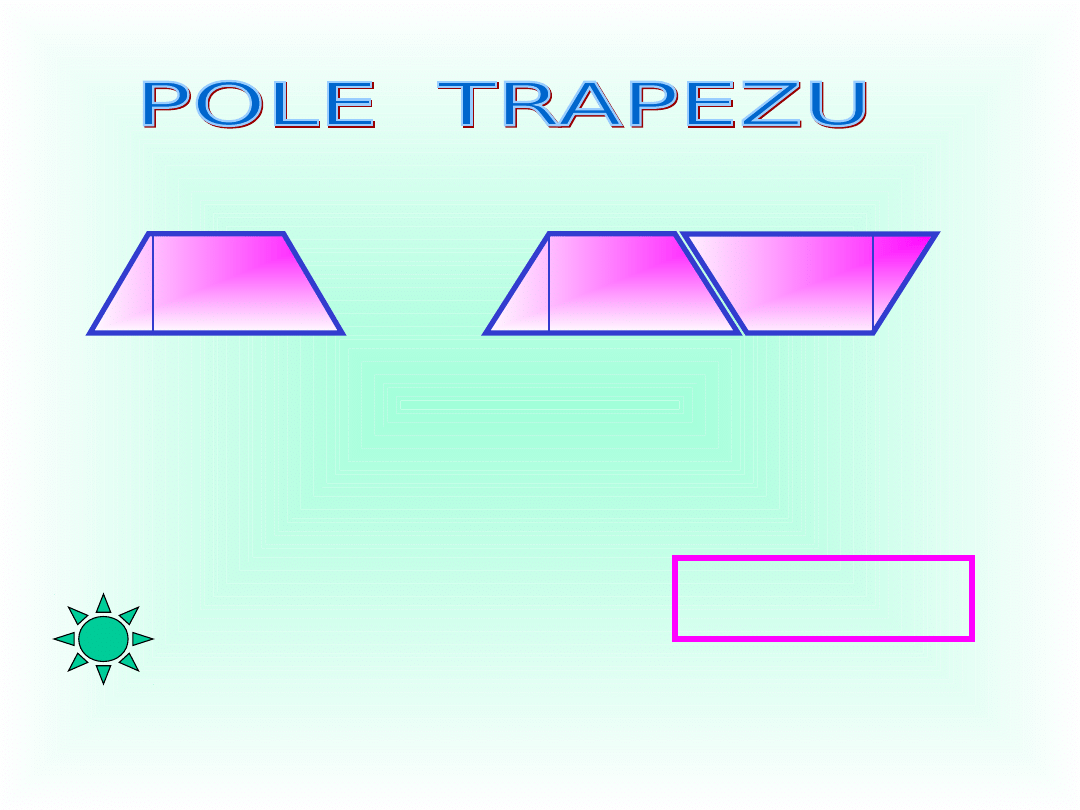
a
a
a
b
b
b
h
h
h
Z dwóch trapezów o podstawach długości a i b oraz wysokości h
można złożyć równoległobok o tej samej wysokości i podstawie
długości (a+b). Pole trapezu wyrażamy następująco:
P = ½(a+b)•h
Pole trapezu równe jest połowie iloczynu
sumy długości podstaw i wysokości.
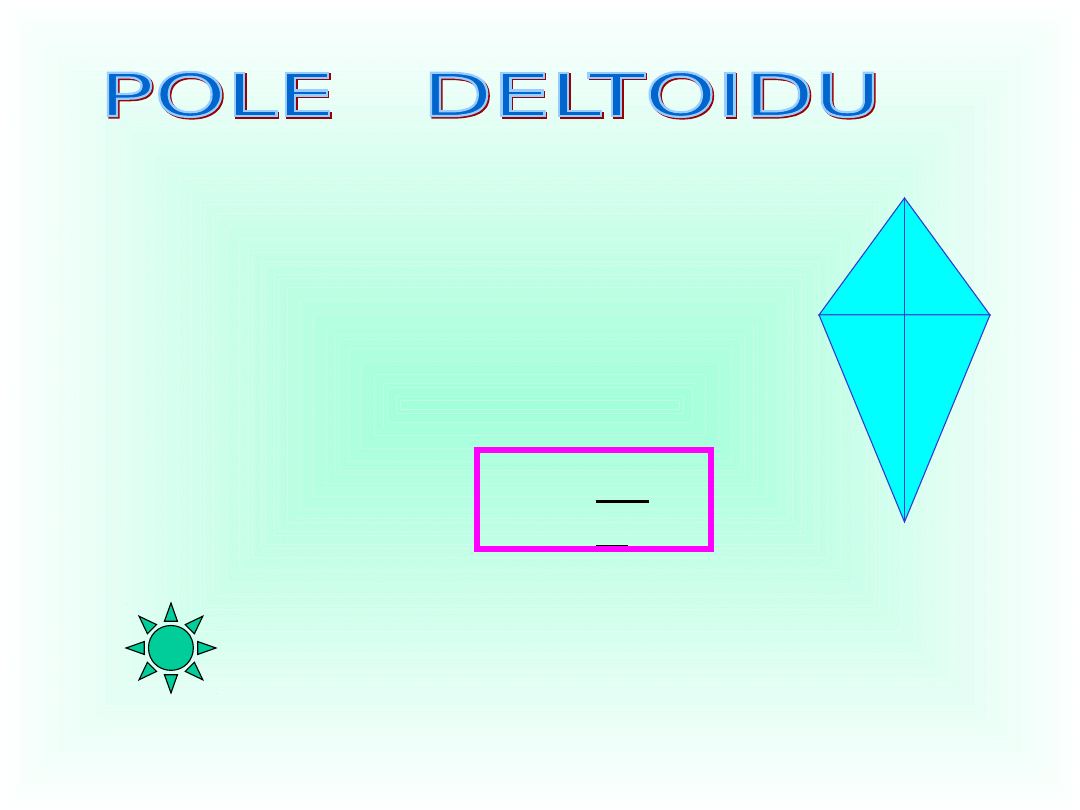
Czworokąt, który ma dwie pary
sąsiednich boków równej długości
nazywamy
deltoidem
(latawcem).
Przekątne deltoidu są prostopadłe.
Punkt przecięcia przekątnych dzieli
jedną z nich na połowy.
f
e
P =
e•
f
2
Pole deltoidu równe jest połowie iloczynu
długości jego przekątnych.

Jak obliczyć pole
sześciokąta ABCDEF ?
A
B
C
D
E
F
Należy podzielić ten sześciokąt na dwa trójkąty
AEF i
ABE
oraz jeden romb BCDE. Obliczyć pola tych trzech figur i dodać
otrzymane wyniki.(Można wykonać inny podział sześciokąta.)

Zadanie 1
Największy skonstruowany na świecie latawiec
miał powierzchnię 553 m² . Ile to arów?
Zadanie 2
Największy wyprodukowany na świecie koc miał
powierzchnię 17 289 m². Ile to hektarów?

Zadanie 3
Okno ma powierzchnię 0,8 m².
Ile to centymetrów kwadratowych?
Zadanie 4
Działka ma powierzchnię 0,03 km².
Ile to metrów kwadratowych?
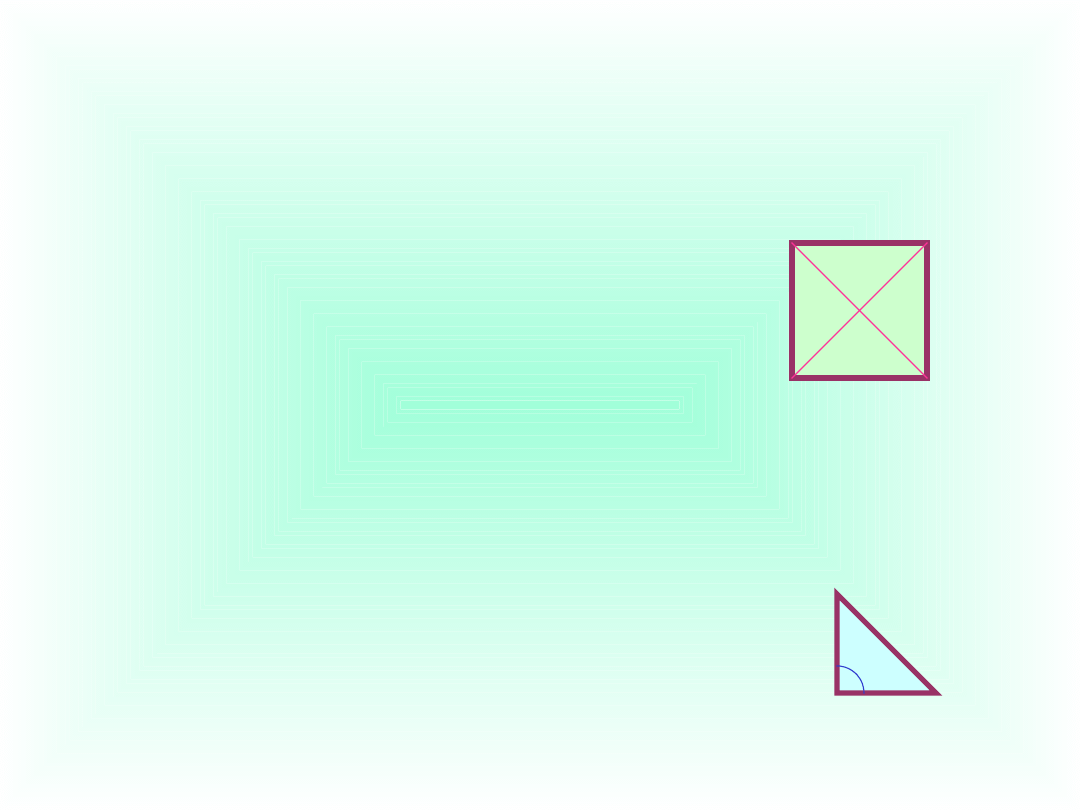
Zadanie 5
Oblicz pole kwadratu o przekątnej 10 cm
(pamiętaj, że każdy kwadrat jest rombem).
Zadanie 6
Oblicz pole trójkąta prostokątnego
równoramiennego o przyprostokątnej 5 dm.
a
a
a
a
•
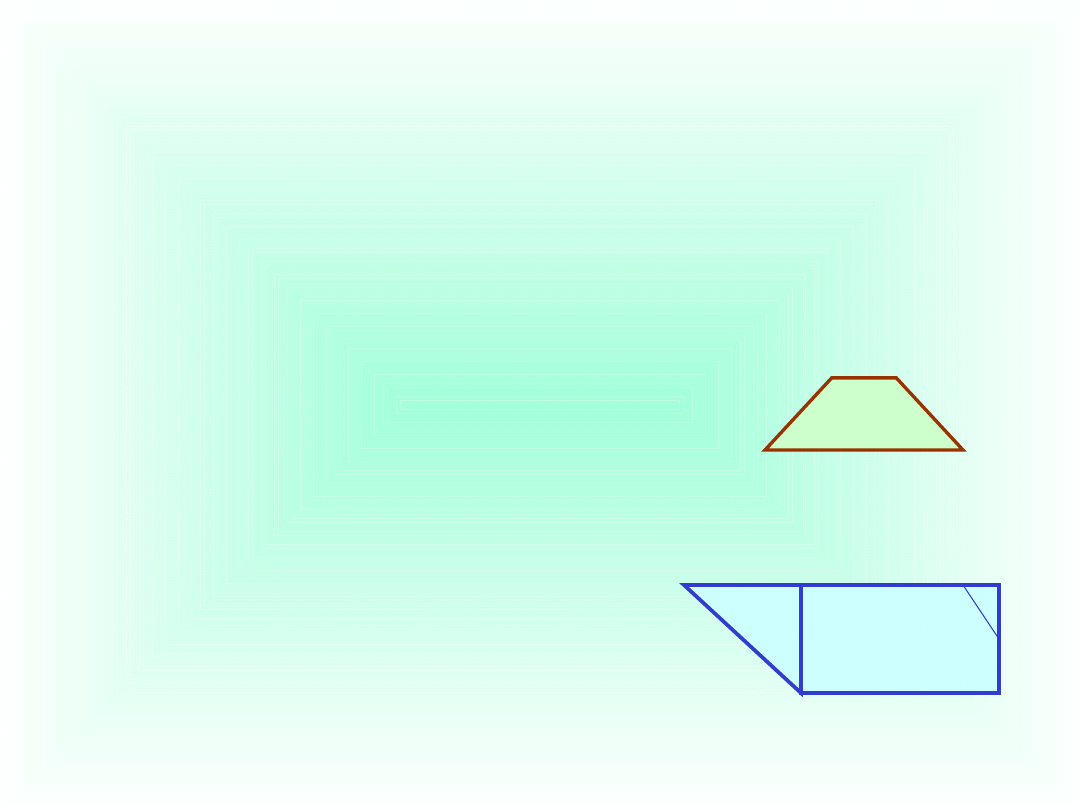
Zadanie 7
Suma długości podstaw trapezu wynosi 35 cm.
Oblicz pole tego trapezu, jeżeli wysokość ma 1,2 dm.
Zadanie 8
Oblicz pole trapezu,
który przedstawiono
na rysunku obok.
45
4cm
3cm
•
°

Zadanie 9
Boki równoległoboku wynoszą 6 cm i 10 cm.
Oblicz wysokości tej figury, jeżeli pole wynosi 33 cm².
Zadanie 10
Pole rombu jest równe 52 cm², a jego wysokość
równa się 6,5 cm. Oblicz obwód tego rombu.
a
a
a
b
h
h
¹
²
h

Zadanie 11
Ramiona trapezu prostokątnego mają długości 4cm i 5 cm.
Pole trapezu jest równe 92 cm². Oblicz obwód tego trapezu.
Zadanie 12
Narysuj w układzie współrzędnych trójkąt KLM o wierzchołkach
K=(0,0), L=(1,-8), M=(-3,-4). Oblicz pole tego trójkąta. Odczytaj
odpowiednie odcinki z układu wpółrzędnych (nie mierz ich linijką).

Zadanie 1 5.53 a
Zadanie 2 1,7289 ha
Zadanie 3 8 000 cm²
Zadanie 4 30 000 m²
Zadanie 5 50 cm²
Zadanie 6 12,5 dm²
Zadanie 7 210 cm² (2,1 dm²)
Zadanie 8 10,5 cm²
Zadanie 9 3,3 cm oraz 5,5 cm
Zadanie 10 32cm
Zadanie 11 55cm
Zadanie 12 14 j²

To już koniec drogi uczniu!
Mam nadzieję, że podobała Ci się ta lekcja.
Jeżeli doszedłeś do tej strony, to znaczy, że
dobrze wywiązałeś się z przedstawionych
zadań. Dziękuję za Twoją pracę na lekcji.
Życzę miłego dnia.
Prezentację w całości
opracowała i wykonała
mgr inż. Anna Berlińska - Komza
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
Wyszukiwarka
Podobne podstrony:
Pola figur płaskich - ćwiczenia, materiały szkolne, wielokąty
pola figur płaskich na bdb
Pola figur płaskich
Pola figur płaskich tekst piosenki 6a
ppt Pola Figur Płaskich
pola figur plaskich
pola figur plaskich
Pola Figur Płaskich Test klasa V
pola figur płaskich zadania
pola figur plaskich
Pola figur płaskich, jednostki
więcej podobnych podstron