Youtube: „Big Perpetuum Mobile”.

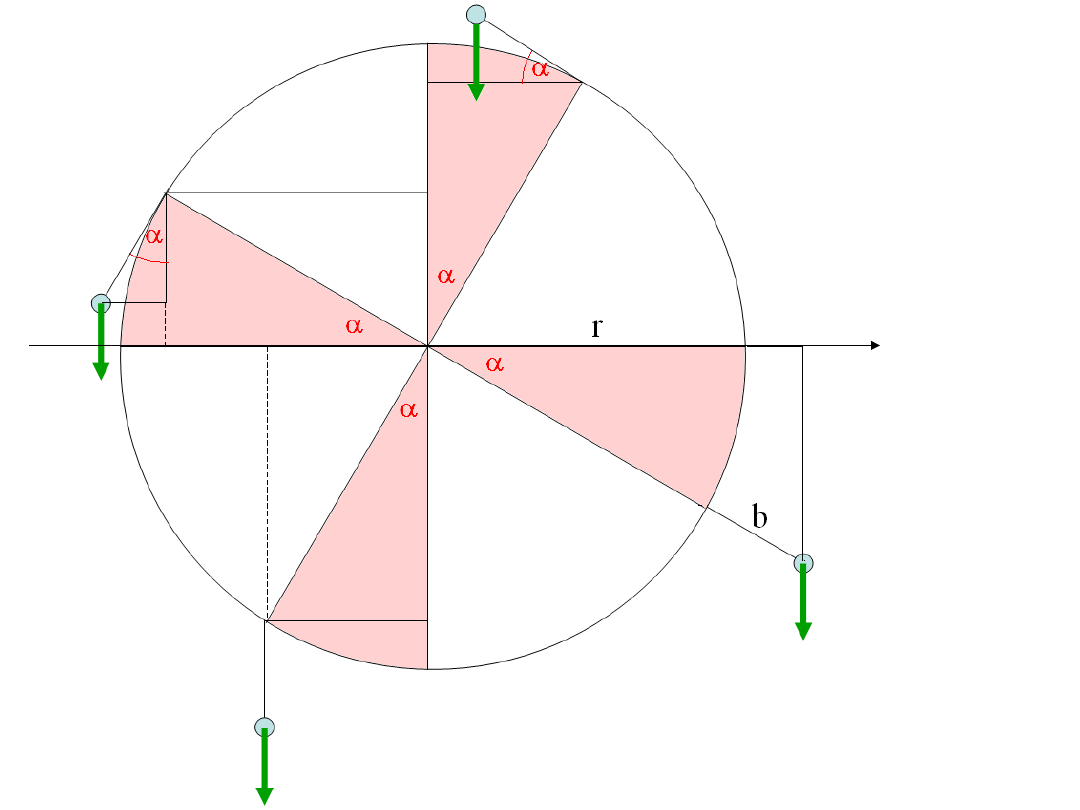
F x

1

= F (r + b)

cos

F x

4

= F (r sin – b

cos

F x

3

= - F (r cos + b

sin

F x

2

= - F r sin

F x

1

= F (r + b)

cos

F x

4

= F (r sin – b

cos

F x

3

= - F (r cos + b

sin

F x

2

= - F r sin

+

F x

1

= F (r + b)

cos

F x

4

= F (r sin – b

cos

F x

3

= - F (r cos + b

sin

F x

2

= - F r sin

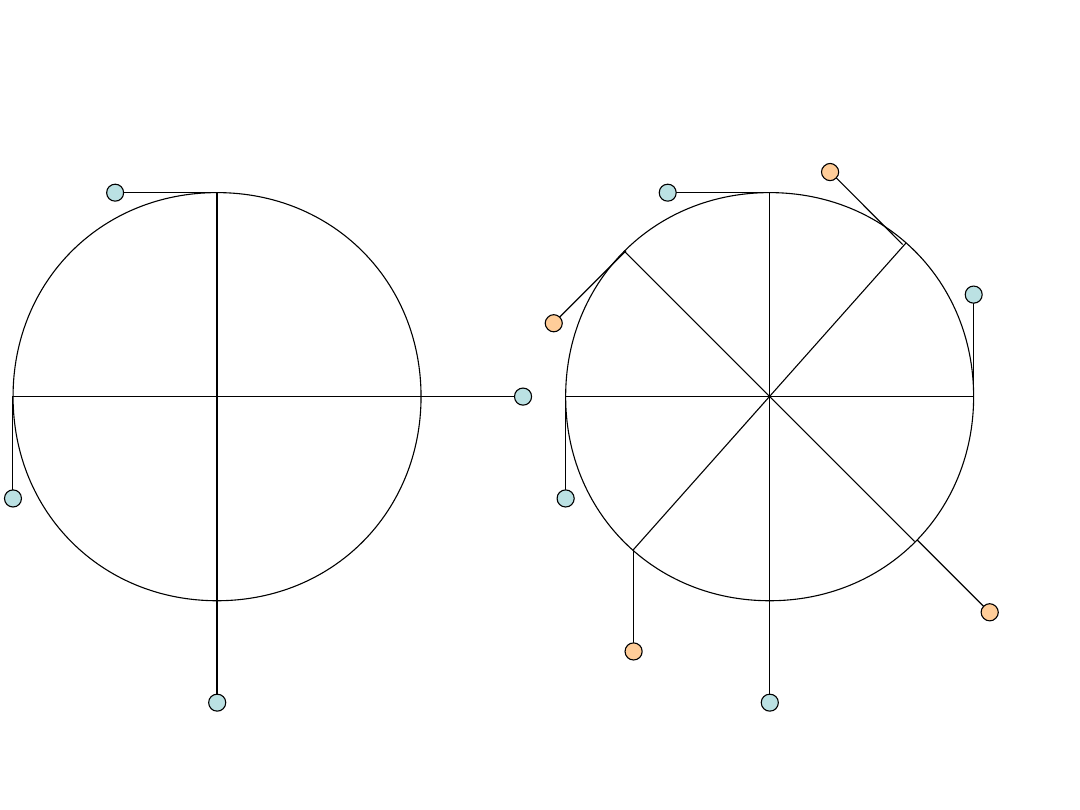
Pokazaliśmy, że dla każdego kąta 

większego od zera, a mniejszego
od 90°, koło chce wykonywać ruch
wsteczny.

A dla  = 0 ?

Wykaż, że jest …
równowaga!

Widzimy, że koło wymaga cały
czas napędu, zwłaszcza gdy jest
więcej kul niż 4. Zestaw niebieski
jest w równowadze, ale
pomarańczowy wytwarza
wsteczny moment siły.

A więc otrzymaliśmy perpetuum mobile, tylko że
się będzie kręcić w drugą stronę.

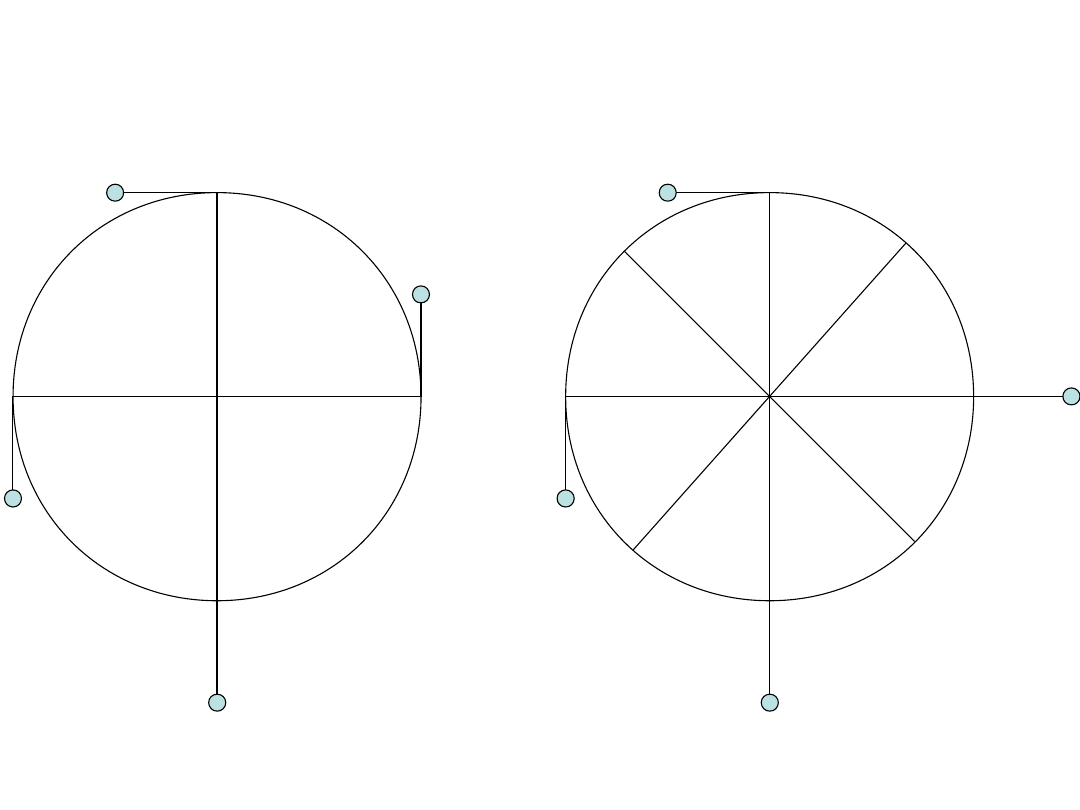
Nim dostaniemy Nagrodę Nobla
zastanówmy się dlaczego trzeba
cały czas pokręcać wykonując
pracę. Otóż kulka która ma się
odchylić wpierw przyjmie
położenie takie jak poniżej.
Nazwijmy to sytuacją A.

Przedtem ramię z kulką było poziome,
teraz kulka jest o b wyżej. Ha! Nasza praca
poszła na dostarczenie kulce dokładnie
mgb energii.

Zaraz kulka opadnie i blokując się poruszy
całe koło. Dostarczy mu dokładnie mgb
energii kinetycznej. Dzięki niej koło drgnie i
będzie mogło obracać się do chwili aż znowu
osiągniemy sytuację A. Wtedy się zatrzyma.
To znaczy, że układ mógłby kręcić się w
nieskończoność, zatrzymując się, to znowu
ruszając.

Niestety aby być perpetuum mobile trzeba energię
produkować, a nie tylko się ruszać zachowując jej
stałą wartość.

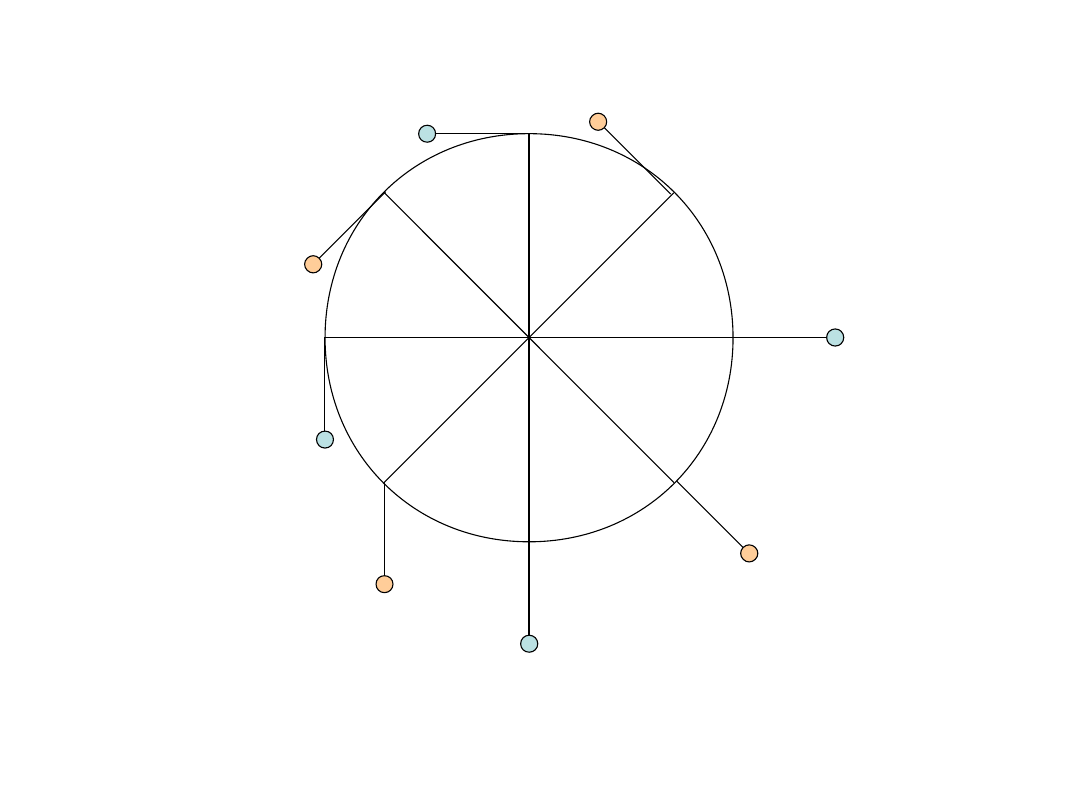
Wykaż, że jeśli pozwolimy kołu obracać się wstecz z pozycji nieruchomej takiej jak poniżej,
to obróci się zaledwie o 45 stopni, a potem ruszy do pozycji wyjściowej i tak będzie
oscylować w nieskończoność, o ile nie będzie tracić energii.

prezentację przygotował

Wiesław Kruczała

Otwock maj 2020