Metody optymalizacji 1

Plan wykładu

• Metody poszukiwania minimum bez

ograniczeń

• Programowanie liniowe
• Metoda Simplex
• Dualność programowania liniowego
• Problemy całkowitoliczbowe
• Metoda podziału i oszacowań
• Metoda podziału i odcięć

Sformułowanie problemu

poszukiwania minimum bez

ograniczeń

Zadanie minimalizacji funkcji bez ograniczeń

można zapisać następująco

gdzie f : R

n

 R , przy czym zakłada się, że

funkcja f jest ograniczona od dołu.

)

(

min

)

ˆ

(

x

x

f

f

n

R





x

Warunki optymalności dla

zadań bez ograniczeń (1)

Definicja. Kierunkiem d w przestrzeni R

n

będziemy

nazywać dowolny n-wymiarowy wektor
kolumnowy. Niech będzie dany punkt x  R

n

oraz

skalar



 [0;+). Dowolny punkt y  R

n

leżący na

półprostej wychodzącej z punktu x w kierunku d 

0 będzie w wówczas określony zależnością

y = x +



d

Warunki optymalności dla

zadań bez ograniczeń (2)

Lemat. Niech f : X = R

n

 R

1

będzie funkcją

różniczkowalną w punkcie x

0

 X . Załóżmy, że

istnieje d, dla którego

f(x

0

)

T

d < 0

wówczas istnieje takie



> 0, że dla wszystkich





(0;



] zachodzi

f(x

0

+



d) < f(x

0

)

Dowód. Lemat wynika wprost z własności różniczki

Gateaux

d

x

x

d

x

T

f

f

f

)

(

)

(

)

(

lim

0

0

0

0

















Warunki optymalności dla

zadań bez ograniczeń (3)

Twierdzenie. Niech f : X = R

n

 R

1

będzie funkcją

różniczkowalną. Jeżeli x



 X minimalizuje funkcję

w tzn.

f(x



)  f(x), x  X

to

f(x



) = 0

Powyższy warunek jest tylko warunkiem

koniecznym. Jeżeli więc f(x



) = 0, to x



może być

minimum lub maksimum globalnym lub lokalnym,
albo punktem przegięcia lub punktem siodłowym.

Warunki optymalności dla

zadań bez ograniczeń (4)

Twierdzenie. Niech f : X = R

n

 R

1

będzie funkcją

wypukłą i różniczkowalną. Punkt x



 X stanowi

minimum globalne funkcji f wtedy i tylko wtedy,
gdy x



spełnia warunek

f(x



) = 0

Twierdzenie. Jeśli f : X = R

n

 R

1

będzie funkcją

ściśle wypukłą i różniczkowalną, to punkt x



 X

spełniający warunek konieczny f(x



) = 0 jest

jednym minimum globalnym funkcji f.

Metody poszukiwania minimum

funkcji bez ograniczeń

• Metody przypadkowe

 Algorytmy genetyczne
 Symulowane wyżarzanie

• Metody zdeterminowane (sposób tworzenia

kierunków poszukiwań)

 Metody o modyfikowanej bazie (bezgradientowe)
 Metody o modyfikowanym kierunku (gradientowe)

• Metody zdeterminowane (sposób

znajdowania kolejnego punktu wzdłuż

kierunku poszukiwań)

 Metody dyskretne
 Metody z minimalizacją

Metoda złotego podziału (1)

• Metoda bezgradientowa
• Stosuje złotą liczbę
• Złota liczba została odkryta przez

starożytnych Greków, i dotyczy podziału
odcinka o długości
(a + b) na takie części, że (a + b) / a = a / b

• Metoda złotego podziału stosuje liczbę (



 1)

• Stosowana w architekturze, sztuce

2

1

5





Metoda złotego podziału (2)

Minimum jest szukane dla funkcji f(x), x  [



0

;



m

]

Inicjalizacja algorytmu



= (



 1) , 



= (1 



)(



m





0

) , a

1

=



0

, b

1

=



m

,

x

11

= a

1

+ 



, x

21

= b

1

 



Algorytm obliczeń
Jeżeli f(x

2k

) > f(x

1k

), to

a

k+1

= a

k

, b

k+1

= x

2k

, x

1k+1

=



a

k+1

+ (1 



)b

k+1

, x

2k+1

= x

1k

Jeżeli f(x

2k

)  f(x

1k

), to

a

k+1

= x

1k

, b

k+1

= b

k

, x

1k+1

= x

2k

, x

2k+1

=



b

k+1

+ (1 



)a

k+1

Warunek stopu
Wymagana dokładność, liczba iteracji

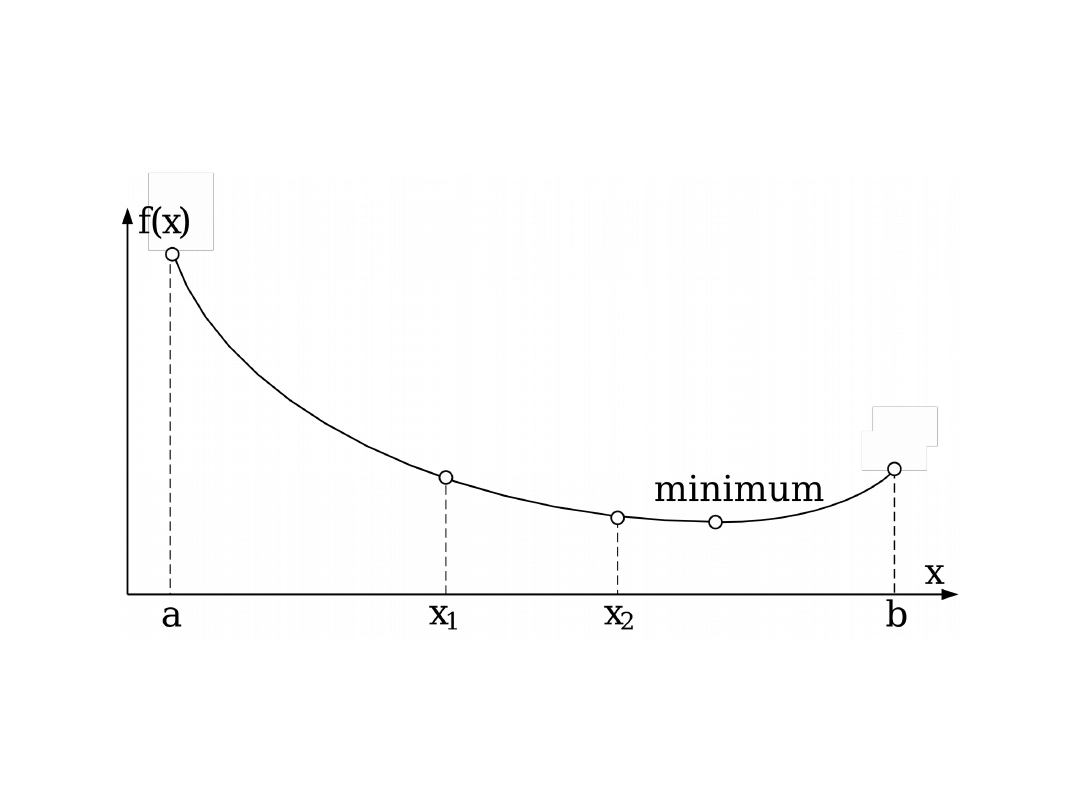
Metoda złotego podziału (3)

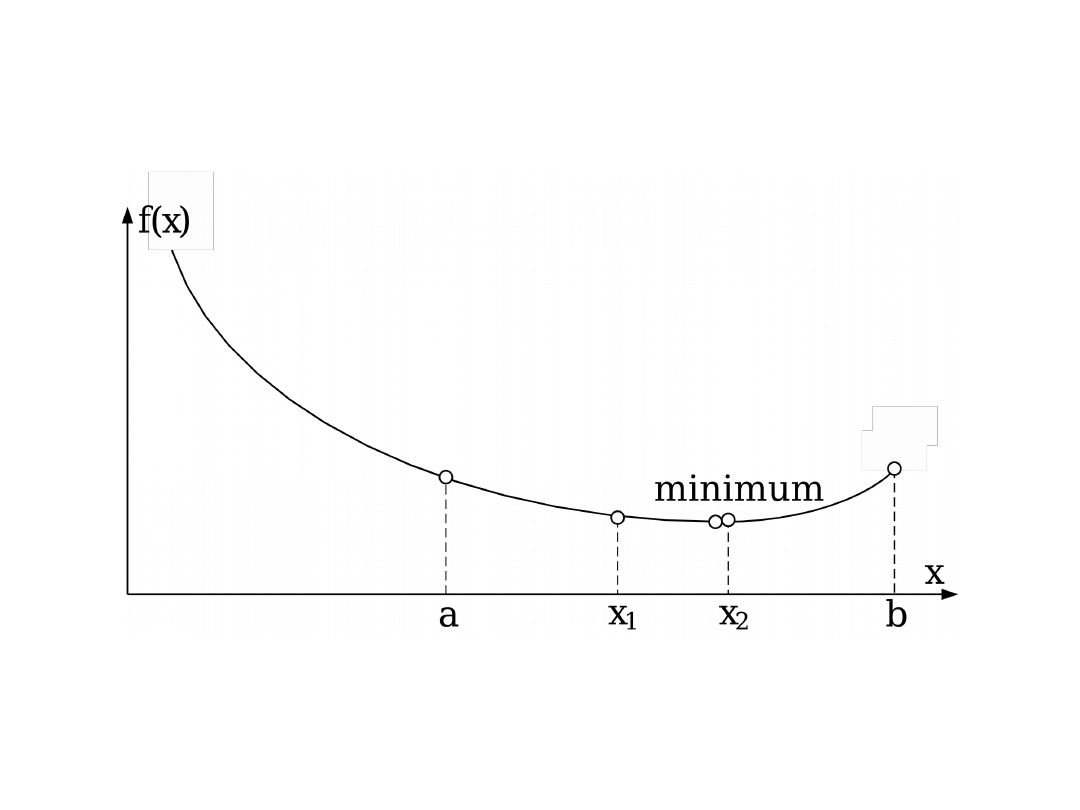
Metoda złotego podziału (3)

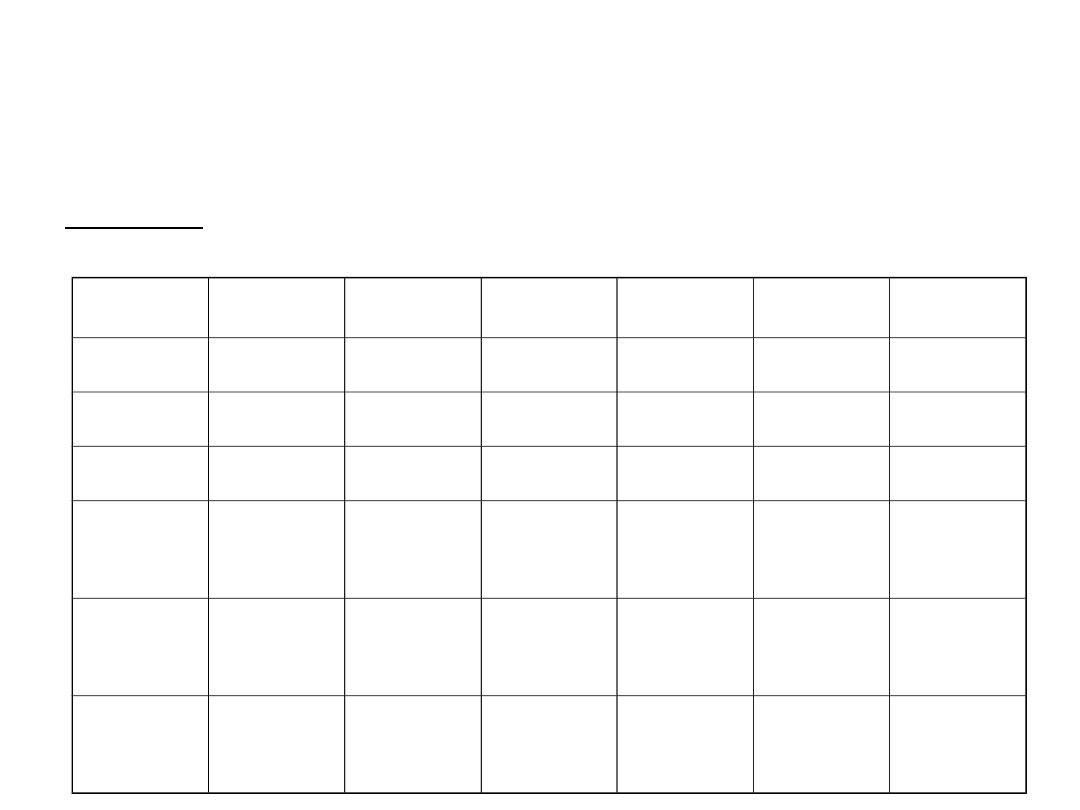
Metoda złotego podziału (4)

Przykład. Znaleźć minimum dla f(x) = x

2

– 6x – 4, x  [0;10]

k

a

b

x

1

x

2

f(x

1

)

f(x

2

)

1

0

10

3,82

6,18

-12,3

-2,8

2

0

6,18

2,36

3,82

-12,6

-12,3

3

0

3,82

1,46

2,36

-10,6

-12,6

4

1,46

3,82

2,36

2,92

-12,6

-

12,99

5

2,36

3,82

2,92

3,26

-

12,99

-

12,93

6

2,36

3,26

2,70

2,92

-

12,91

-

12,99

Jakie jest rozwiązanie tego problemu?

Programowanie liniowe

• Programowanie liniowe LP (ang. Linear

Programming) to klasa problemów programowania
matematycznego, w której wszystkie warunki
ograniczające oraz funkcja celu mają postać liniową

• Wiele problemów optymalizacji szczególnie w

ekonomii może być zapisana jako zadanie
programowania liniowego

• Najbardziej popularna metoda rozwiązania zadań

programowania liniowego to Simplex

• Twórca metody Simplex – George Dantzig –

otrzymał w 1975 roku nagrodę Nobla w dziedzinie
ekonomii

Warianty zapisu zadania

programowania liniowego (1)

indeksy

j = 1,2,…,n zmienne

i = 1,2,…,m ograniczenia

stałe

a

ij

współczynnik zmiennej j w ograniczeniu i

b

i

prawa strona ograniczenia i

c

j

współczynnik kosztu zmiennej j

zmienne

x

j

zmienna j

funkcja kryterialna

min z = 

j

c

j

x

j

ograniczenia



j

a

ij

x

j

= b

i

dla i = 1,2,…,m

x

j

 0 dla j = 1,2,…,n

Warianty zapisu zadania

programowania liniowego (2)

x = [x

1

, x

2

,…, x

n

] – kolumna o rozmiarze n

b = [b

1

, b

2

,…, b

m

] – kolumna o rozmiarze m

c = [c

1

, c

2

,…, c

n

] – wiersz o rozmiarze n

macierz o rozmiarze m x n

min cx
przy ograniczeniach (p.o.)
Ax = b
x  0



























mn

m

n

n

a

a

a

a

a

a

...

...

...

...

...

...

1

2

21

1

11

A

Postać standardowa zadania

programowania liniowego (1)

zmienne
x

j

zmienna j

funkcja kryterialna
min z = 

j

c

j

x

j

ograniczenia


j

a

ij

x

j

= b

i

dla i = 1,2,…,m

x

j

 0 dla j = 1,2,…,n

Postać standardowa zadania

programowania liniowego (2)

Pełne ograniczenia nierównościowe typu 



j

a

ij

x

j

 b

i

dla i = 1,2,…,m

można sprowadzić do postaci równościowej przez

dodanie zmiennej dopełniającej (ang. slack) z o

wartościach nieujemnych



j

a

ij

x

j

+ z

j

= b

i

, z

i

 0 dla i = 1,2,…,m

Pełne ograniczenia nierównościowe typu 



j

a

ij

x

j

 b

i

dla i = 1,2,…,m

przekształcamy przez odjęcie zmiennej

dopełniającej o wartościach nieujemnych



j

a

ij

x

j

–

z

j

= b

i

, z

i

 0 dla i = 1,2,…,m

Postać standardowa zadania

programowania liniowego (3)

Pełne dwustronne ograniczenia nierównościowe

l

i

 

j

a

ij

x

j

 u

i

dla i = 1,2,…,m



j

a

ij

x

j

 u

i

dla i = 1,2,…,m



j

a

ij

x

j

 l

i

dla i = 1,2,…,m

Mogą być sprowadzone do postaci równościowej

dodając zmienne dopełniające do ograniczeń



j

a

ij

x

j

 u

i

dla i = 1,2,…,m



j

a

ij

x

j

 l

i

dla i = 1,2,…,m

w przedstawiony powyżej sposób

Postać standardowa zadania

programowania liniowego (4)

Dwustronne ograniczenia zakresu zmiennych

l

j



x

j

 u

j

dla j = 1,2,…,n

można zastąpić nierównościami

x

j

 l

j

dla j = 1,2,…,n

x

j

 u

j

dla j = 1,2,…,n

Zmienne nieograniczone można zastąpić

wprowadzając różnicę dwóch nieujemnych zmiennych

x

j

= z

1

– z

2

z

1

 0

z

2

 0

Własności zadania

programowania liniowego

Twierdzenie. Zbiór wszystkich rozwiązań

dopuszczalnych zadania programowania liniowego
jest zbiorem wypukłym

Twierdzenie. Funkcja celu zadania programowania

liniowego przyjmuje wartość minimalną w
punkcie wierzchołkowym zbioru wypukłego
utworzonego na zbiorze rozwiązań dopuszczalnego
zadania programowania liniowego. Jeżeli przyjmuje
wartość w więcej niż jednym punkcie
wierzchołkowym, to tę samą wartość przyjmuje dla
każdej kombinacji wypukłej tych punktów

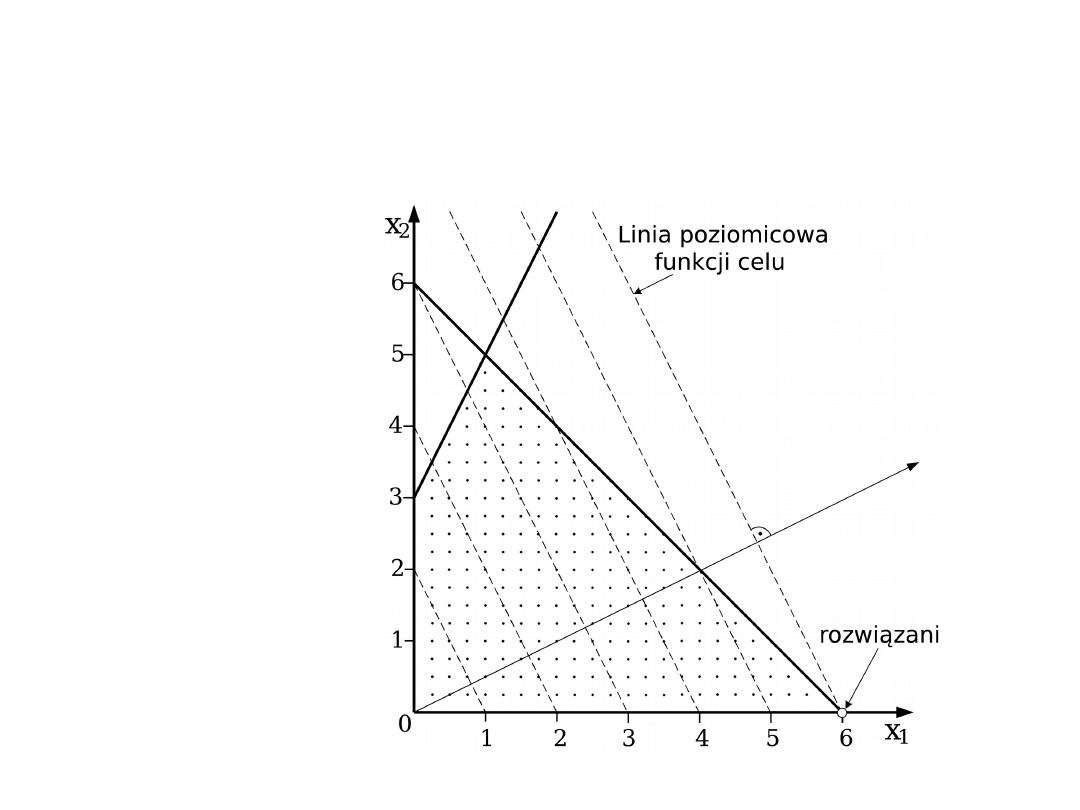
Interpretacja geometryczna

programowania liniowego (1)

max 2x

1

+ x

2

p.o.
x

1

+ x

2

 6

-2x

1

+ x

2

 3

x

1

 0

x

2

 0

rozwiązanie
x

1

= 6

x

2

= 0

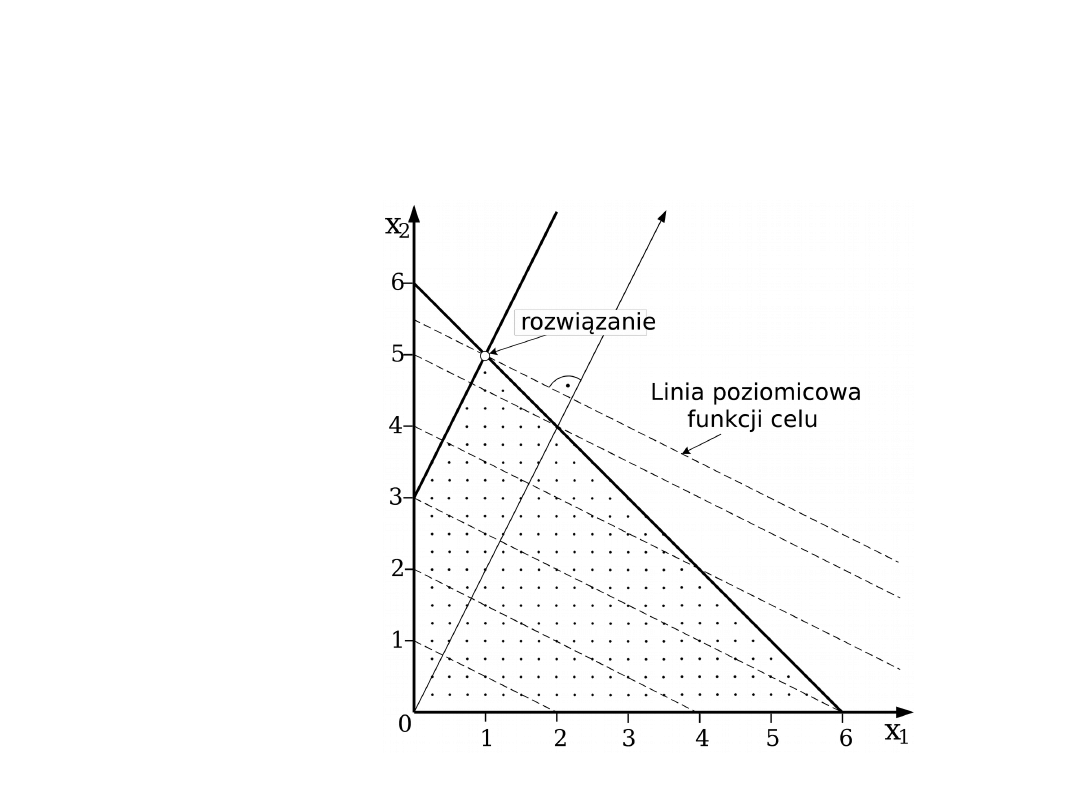
Interpretacja geometryczna

programowania liniowego (2)

max x

1

+ 2x

2

p.o.
x

1

+ x

2

 6

-2x

1

+ x

2

 3

x

1

 0

x

2

 0

rozwiązanie
x

1

= 1

x

2

= 5

Metoda Simplex

• Opracowana w 1947 roku przez Georga Dantziga
• Istota metody simpleks polega na przeglądaniu

wierzchołków wielościanu przestrzeni rozwiązań

• Wyznaczany jest jeden z wierzchołków
• Kolejne kroki algorytmu polegają na przejściu do

następnego wierzchołka, znajdującego się na
jednej krawędzi z odnalezionym już punktem, w
którym funkcja celu osiąga lepsze wartości

• Algorytm kończy się, gdy kolejny przeglądany punkt

wierzchołkowy jest najlepszy pod względem
odpowiednich wartości funkcji celu

Dualność

programowania liniowego (1)

• Wiele metod rozwiązywania zadań

programowania liniowego wykorzystuje

zadania dualne

• Z zadaniem podstawowym, zwanym zadaniem

pierwotnym lub prymalnym jest związane

zadanie dualne

• Między zadaniem podstawowym i dualnym są

ścisłe związki umożliwiające konstrukcję

algorytmów rozwiązywania zadań

programowania liniowego, jak również

zmniejszenie nakładu obliczeń

Dualność

programowania liniowego (2)

Zadanie prymalne
zmienne
x

j

zmienna j

funkcja kryterialna
min 

j

c

j

x

j

ograniczenia


j

a

ij

x

j

 b

i

dla i = 1,2,

…,m

x

j

 0 dla j = 1,2,…,n

Zadanie dualne
zmienne



i

dualna zmienna i

funkcja kryterialna
max 

i

b

i



i

ograniczenia


i

a

ij



i

 c

j

dla j = 1,2,

…,n



i

 0 dla i = 1,2,…,m

Dualność

programowania liniowego (3)

Zadanie prymalne
min cx
p.o. Ax  b
x  0

Zadanie dualne
max b
p.o. A  c
  0

Dualność

programowania liniowego (4)

Twierdzenie. Zadaniem dualnym do zadania

dualnego jest zadanie prymalne

Twierdzenie. Jeżeli x jest rozwiązaniem

dopuszczalnym dla zadaniem prymalnego i  jest

rozwiązaniem dopuszczalnym dla zadania
dualnego, to wartość funkcji celu w zadaniu
prymalnym nie może być mniejsza od wartości
funkcji celu w zadaniu dualnym

cx  b

Dualność

programowania liniowego (5)

Twierdzenie (silna dualność). Jeżeli dla pary rozwiązań

dopuszczalnych (x

0

,

0

) zachodzi równość cx

0

= b

0

to (x

0

,

0

) jest parą rozwiązań optymalnych

Twierdzenie. Jeśli jedno z pary wzajemnie dualnych

zadań programowania liniowego ma rozwiązanie
optymalne, to ma je również zadanie dualne i
obydwa zadania mają identyczne wartości funkcji
celu

Twierdzenie. Jeśli zadanie dualne jest nieograniczone,

to zadania prymalne jest sprzeczne

Problemy całkowitoliczbowe

(1)

• Problem, w którym część zmiennych jest ciągła a

część całkowitych określany jest skrótem MIP (ang.

Mixed Integer Programming)

• Problem, w którym wszystkie zmienne są całkowite

określany jest skrótem IP (ang. Integer Programming)

• Problemy całkowitoliczbowe należą do klasy

problemów NP-trudnych

• Specjalną klasą problemów całkowitoliczbowych są

problemy, w których zmienne całkowite mogą

przyjmować wartości 0 lub 1

• Podstawowy sposób rozwiązywania problemów

całkowitoliczbowych to metoda podziału i

oszacowań

Problem MIP

indeksy
j = 1,2,…,n zmienne
i = 1,2,…,m ograniczenia
stałe
a

ij

współczynnik zmiennej j w ograniczeniu i

b

i

prawa strona ograniczenia i

c

i

współczynnik kosztu zmiennej j

zmienne
x

j

zmienna j

funkcja kryterialna
min z = 

j

c

j

x

j

ograniczenia


j

a

ij

x

j

= b

i

dla i = 1,2,…,m

x

j

 {0,1} dla j = 1,2,…,k , x

j

 0 dla j = k + 1, k + 2,…,n

Problem IP

indeksy
j = 1,2,…,n zmienne
i = 1,2,…,m ograniczenia
stałe
a

ij

współczynnik zmiennej j w ograniczeniu i

b

i

prawa strona ograniczenia i

c

i

współczynnik kosztu zmiennej j

zmienne
x

j

zmienna j

funkcja kryterialna
min z = 

j

c

j

x

j

ograniczenia


j

a

ij

x

j

= b

i

dla i = 1,2,…,m

x

j

 {0,1} dla j = 1,2,…,n

Relaksacja problemu MIP

Niech N

0

oraz N

1

oznaczają zbiór oznaczają zbiory

indeksów zmiennych o wartościach 0 oraz 1. Zbiór

N

U

zawiera indeksy zmiennych binarnych o

nieustalonych wartościach

Problem MIP można przekształcić w problem, w

którym są następujące ograniczenia

x

j

 0 dla j = k + 1, k + 2,…,n

0  x

j

 1 , x

j

ciągłe dla j  N

U

x

j

= 0 dla j  N

0

x

j

= 1 dla j  N

1

Rozwiązanie powyższego problemu, jeżeli istnieje,

stanowi dolne oszacowanie rozważanego problemu

Metoda podziału i oszacowań

(1)

• Metoda podziału i oszacowań (ang. branch-and-bound)

polega na przeszukiwaniu przestrzeni rozwiązań i
eliminowaniu podzbiorów przestrzeni rozwiązań, które
nie dają szans na uzyskanie lepszego rozwiązania

• Najważniejsze elementy metody podziału i oszacowań to

oszacowanie (ang. bounding) i podział (ang.
branching)

• Procedura dolnego oszacowania umożliwia

zweryfikowanie bieżącego rozwiązania, zazwyczaj
dolne oszacowanie uzyskuje się rozwiązując
uproszczoną wersję problemu

• Metody podziału służą do wyboru zmiennych do

podstawienie

• Rozwiązanie uzyskane za pomocą metody podziału i

oszacowań można przedstawić w formie drzewa

Metoda podziału i oszacowań

(2)

procedure BBB (N

U

,N

0

,N

1

)

begin
solution (N

U

,N

0

,N

1

, x, z) {solving the relaxed linear poblem};

if N

U

= ∅ or for all i  N

U

x

i

are binary then

if z < z

best

then begin z

best

:= z; x

best

:= x end

else {in the current solution the value of x

i

is not binary for

some i  N

U

}

if z ≥ z

best

then

return {bounding}
else
begin {branching}
choose i  N

U

such that x

i

is fractional;

BBB (N

U

\{i},N

0

 {i},N

1

);

BBB (N

U

\{i},N0,N

1

 {i})

end
end { procedure }

Metoda podziału i odcięć

• Metoda podziału i odcięć (ang. branch-and-cut)

to ulepszona wersja metody podziału i oszacowań

• Skuteczność metody podziały i oszacowań

zależy od efektywności oszacowań

• Wprowadzając w każdym węźle drzewa rozwiązań

dodatkowych ograniczeń (valid
inequalities), można ograniczyć przestrzeń
rozwiązań i uzyskać dokładniejsze oszacowanie

• Metoda podziału i odcięć to metoda podziału i

oszacowań z dodatkowymi ograniczeniami
używanymi w węzłach drzew

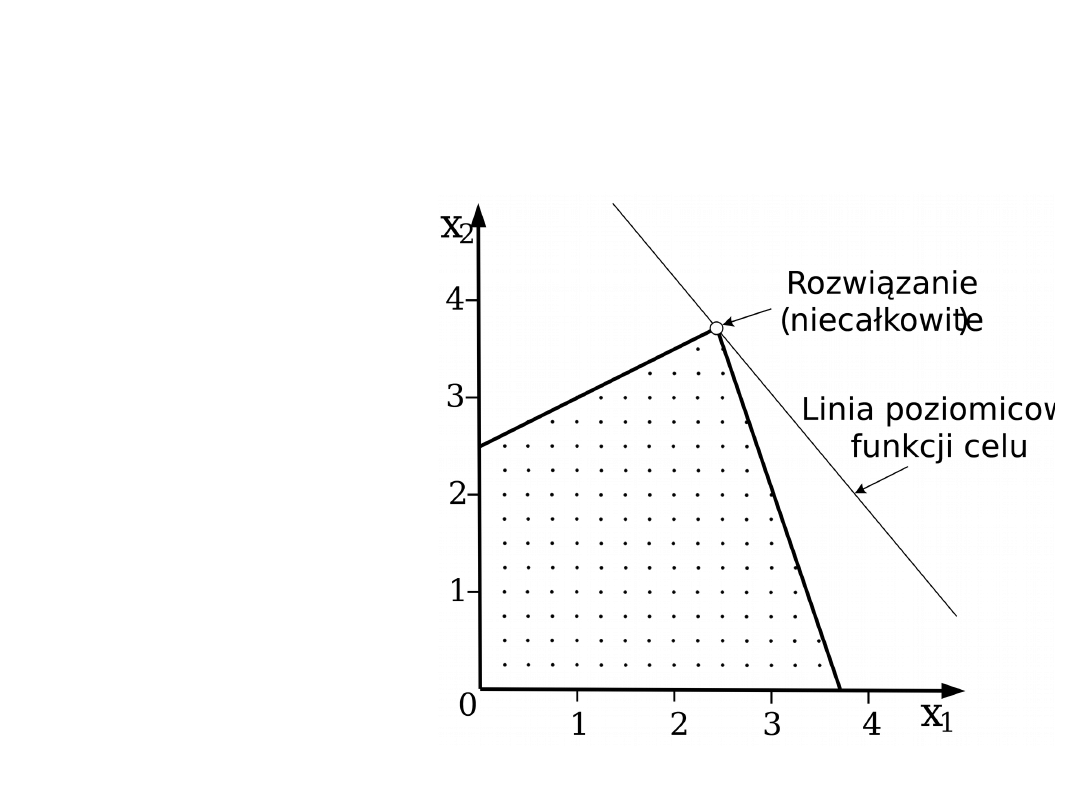
Metoda podziału i odcięć –

przykład (1)

min z = -6x

1

– 5x

2

p.o. 3x

1

+ x

2

 11

-x

1

+ 2x

2

 5

x

1

, x

2

 0, całkowite

rozwiązanie LP
(niecałkowite)
x

1

= 2

3

/

7

x

2

= 3

5

/

7

z = -33

1

/

7

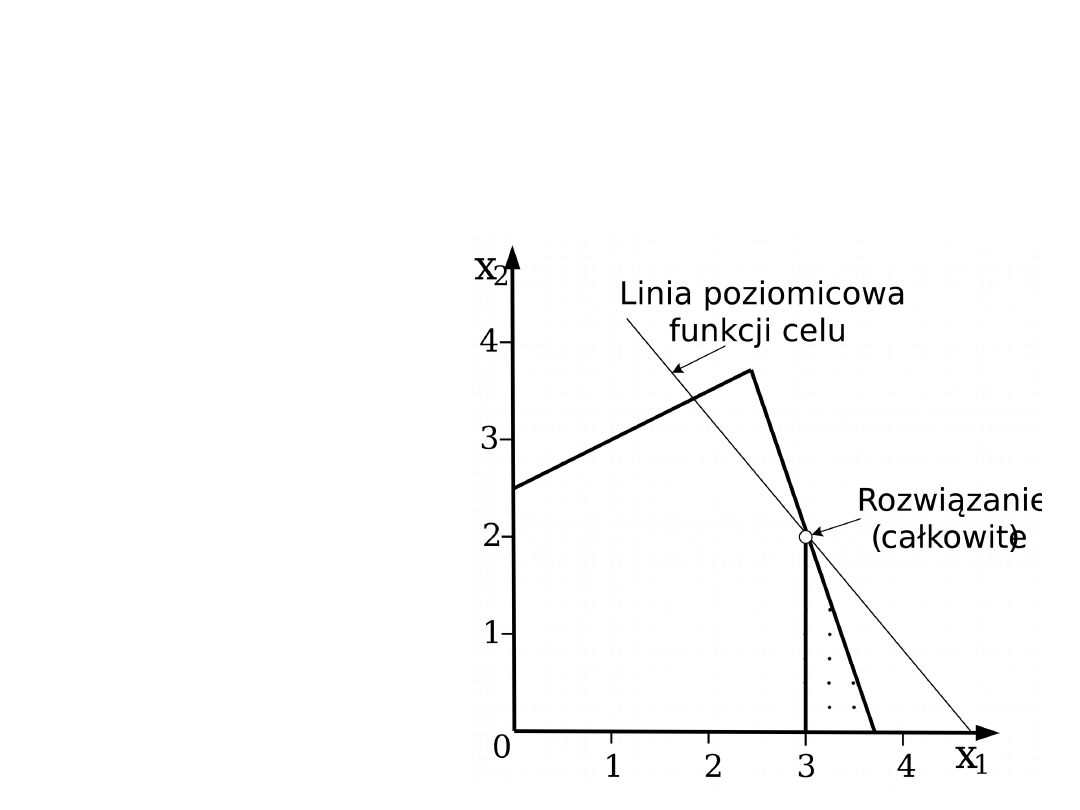
Metoda podziału i odcięć –

przykład (2)

Podział na dwa problemy względem zmiennej x

1

(x

1

 3, x

1

 2)

min z = -6x

1

– 5x

2

p.o. 3x

1

+ x

2

 11

-x

1

+ 2x

2

 5

x

1

 3

x

1

, x

2

 0,

całkowite
rozwiązanie LP
(całkowite)
x

1

= 3 x

2

= 2

z = -28
Koniec obliczeń dla
tego podproblemu

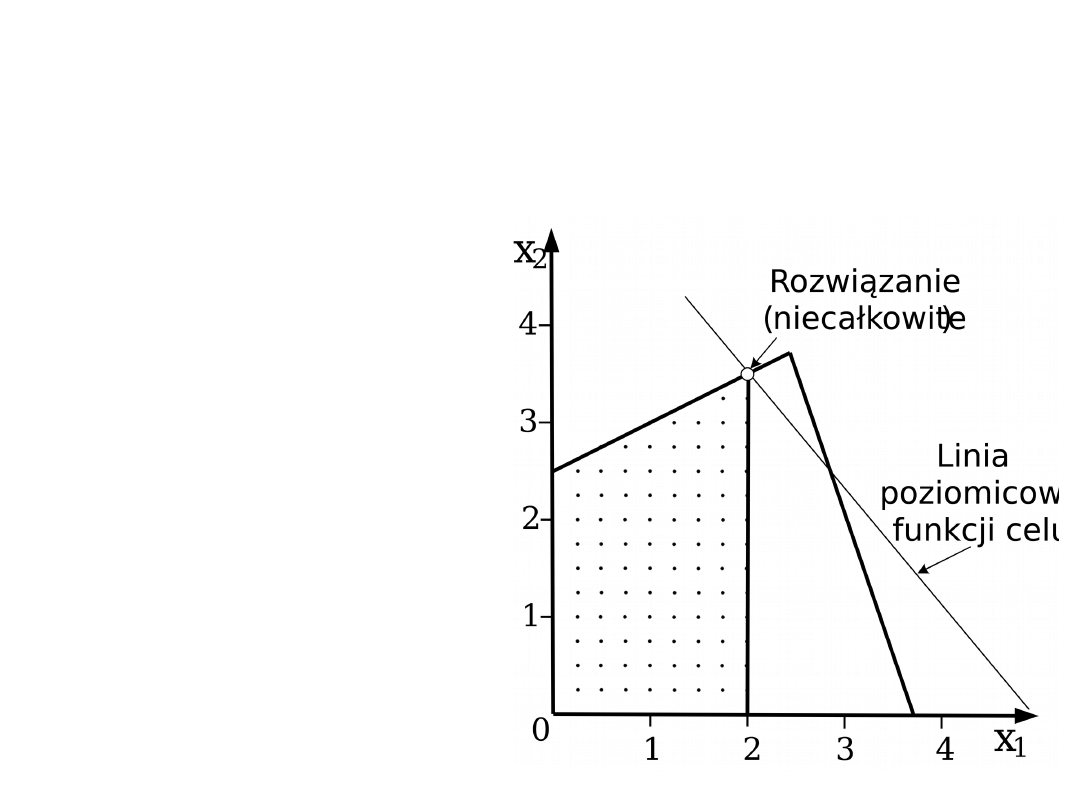
Metoda podziału i odcięć –

przykład (3)

min z = -6x

1

– 5x

2

p.o. 3x

1

+ x

2

 11

-x

1

+ 2x

2

 5

x

1

 2

x

1

, x

2

 0,

całkowite
rozwiązanie LP
(niecałkowite)
x

1

= 2 x

2

= 3,5

z = -29,5
Rozwiązanie nie
spełnia warunku
całkowitoliczbowości,
należy kontynuować
obliczenia

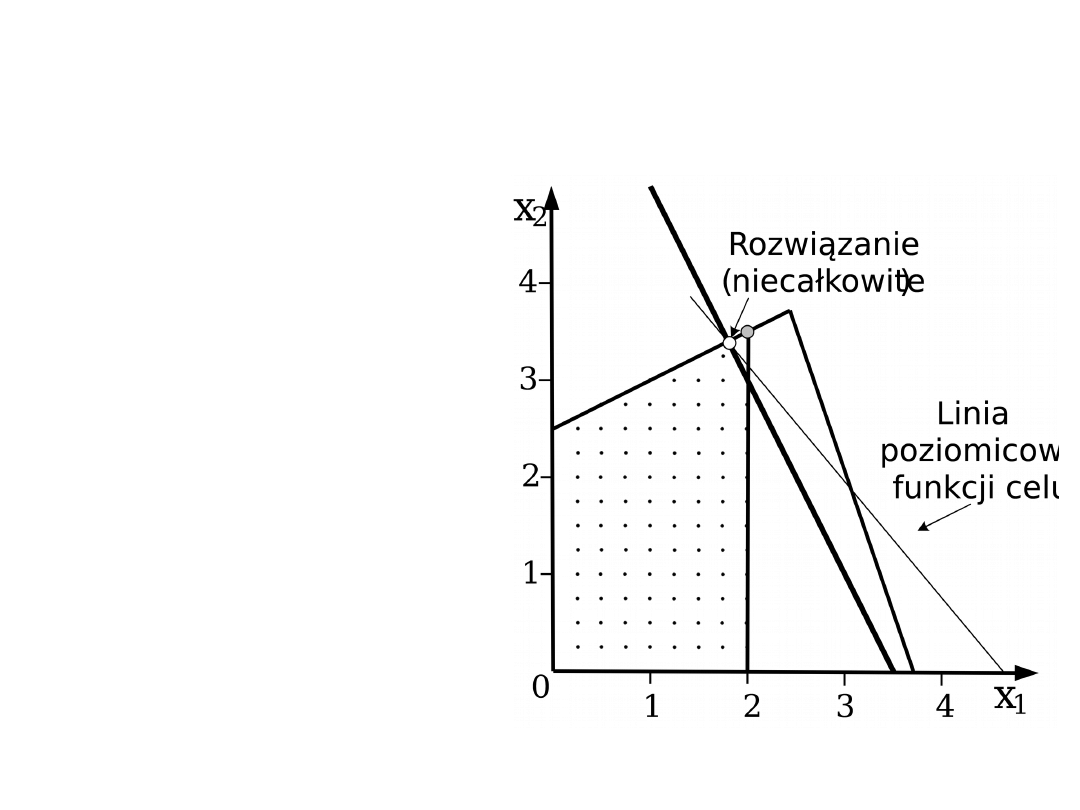
Metoda podziału i odcięć –

przykład (4)

Dodano nowe ograniczenie
min z = -6x

1

– 5x

2

p.o. 3x

1

+ x

2

 11

-x

1

+ 2x

2

 5

x

1

 2

2x

1

+ x

2

 7

x

1

, x

2

 0, całkowite

rozwiązanie LP (niecałkowite)
x

1

= 1,8

x

2

= 3,4

z = -27,8
Otrzymana wartość jest większa niż dotychczas

znalezione rozwiązanie całkowitoliczbowe, koniec
obliczeń

Podsumowanie

• Wiele problemów optymalizacji to zadania

programowania liniowego, w których funkcja

kryterialna oraz ograniczenia są funkcjami

liniowymi, zmienne są ciągłe

• Najbardziej popularna metoda rozwiązywania

zadań programowania liniowego to Simplex

• Zadania, w których część zmiennych musi być

całkowita, należą do klasy NP.

• Jedynymi metodami rozwiązującymi zadania

całkowitoliczbowe to algorytmy oparte na

metodzie podziału i oszacowań

• Efektywną modyfikacją metody podziału i

oszacowań to metoda podziału i odcięć

Dodatkowa literatura

• M. Pióro, D. Medhi, „Routing, Flow, and Capacity Design in

Communication and Computer Networks”, Morgan Kaufman

Publishers 2004 (rozdział 5)

• W. Findeisen, J. Szymanowski, A. Wierzbicki, „Teoria i metody

obliczeniowe optymalizacji”, PWN, Warszawa 1980

• A. Stachurski, A. Wierzbicki, „Podstawy optymalizacji”, Oficyna

Wydawnicza Politechniki Warszawskiej, Warszawa 1999

• S. Gass, „Programowanie liniowe”, PWN, Warszawa 1973

• J. Buga, I. Nykowski, „Zagadnienia transportowe w programowaniu

liniowym”, PWN, Warszawa 1974

• I. Nykowski, „Programowanie liniowe”, PWE, Warszawa 1980

•

http://www.wikipedia.org

•

http://www-unix.mcs.anl.gov/otc/Guide/faq/linear-programming-faq

.html#Q2

•

http://www.ee.ucla.edu/ee236a/ee236a.html

• J. Mitchell, „Branch-and-cut methods for combinatorial optimization

problems”, in the Handbook of Applied Optimization, Oxford

University Press 2002, http://www.rpi.edu/~mitchj/papers/bc_hao.pdf